【算法】【动规】回文串系列问题
文章目录
- 跳转汇总链接
- 3.1 回文子串
- 3.2 最长回文子串
- 3.3 分割回文串 IV
- 3.4 分割回文串II(hard)
跳转汇总链接
👉🔗动态规划算法汇总链接
3.1 回文子串
🔗题目链接
给定一个字符串 s ,请计算这个字符串中有多少个回文子字符串。
具有不同开始位置或结束位置的子串,即使是由相同的字符组成,也会被视作不同的子串。
- 状态表示
- dp[i][j] 表示字符串 s 中以 i 位置开头 j 位置结尾的子串,是否是回文。
- 状态转移方程
-
分析 dp 表,要判断 [i, j] 位置的子串是否为回文,首先要根据 s[i] 和 s[j] 的大小判定,具体如下:
s[i] != s[j], false s[i] == s[j], i == j, truei + 1 == j, truej - i > 1, s[i+1][j-1] == true, trues[i+1][j-1] == false, false
-
- 初始化
- 这里主要是[i+1][j-1] 可能会超出需要范围,但是有个隐含条件 i <= j,可以在 for 循环中控制,所以不需要初始化。
- 填表顺序
- 填写 dp[i][j],需要有 [i+1] 和 [j-1],故二维数组从下往上填写。
- 返回值
- dp 中的 true 的出现次数。
🐎代码如下:
class Solution {
public:int countSubstrings(string s) {int n = s.size();vector<vector<bool>> dp(n, vector<bool>(n));int ret = 0;for(int i = n - 1; i >= 0; i--){for(int j = i; j < n; j++){// 默认都是 false,只需要处理 true 的位置if(s[i] == s[j])dp[i][j] = i + 1 < j ? dp[i+1][j-1] : true;if(dp[i][j])ret++;}}return ret;}
};
3.2 最长回文子串
🔗题目链接
给你一个字符串 s,找到 s 中最长的回文子串。
如果字符串的反序与原始字符串相同,则该字符串称为回文字符串。
如上题分析,写 dp 方程。
在 dp[i][j] 且满足基本约束时,找到 len(即 j - i + 1)的最大值,
同时,由于 dp 表是从下往上(从后往前)填的,正好更新 begin。
🐎代码如下:
class Solution {
public:string longestPalindrome(string s) {int n = s.size();int len = 1, begin = 0;vector<vector<bool>> dp(n, vector<bool>(n));for(int i = n - 1; i >= 0; i--){for(int j = i; j < n; j++){if(s[i] == s[j])dp[i][j] = i+1 < j ? dp[i+1][j-1] : true;if(dp[i][j] && j-i+1 > len)len = j - i + 1, begin = i;}}return s.substr(begin, len);}
};
3.3 分割回文串 IV
🔗题目链接
给你一个字符串 s ,如果可以将它分割成三个 非空 回文子字符串,那么返回 true ,否则返回 false 。
当一个字符串正着读和反着读是一模一样的,就称其为 回文字符串 。
还是照上述方法,生成 dp 表,记录是否为回文子串,进行数据预处理;
再将字符分成三部分,依次遍历,如果 相应位置的 dp 值为 true,就可以直接返回啦。
🐎代码如下:
class Solution {
public:bool checkPartitioning(string s) {int n = s.size();// 1. 预处理:子串是否是回文vector<vector<bool>> dp(n, vector<bool>(n));for(int i = n - 1; i >= 0; i--)for(int j = i; j < n; j++)if(s[i] == s[j])dp[i][j] = i+1 < j ? dp[i+1][j-1] : true;// 2. 字符串分成三段,枚举就好了// [0, i) [i, j) [j, n)for(int i = 1; i < n - 1; i++) // i 是第二段的起始for(int j = i + 1; j < n; j++) // j 是第三段的起始if(dp[0][i-1] && dp[i][j-1] && dp[j][n-1])return true;return false;}
};
3.4 分割回文串II(hard)
🔗题目链接
给你一个字符串 s,请你将 s 分割成一些子串,使每个子串都是回文。
返回符合要求的 最少分割次数 。
同样先预处理数据,方便判断子串是否是回文串;
剩下的分析方法与 1.4 单词拆分题 一样:
- dp[i] 表示 s[0, i] 位置上的最长字串的最小分割次数;
- 当分析 dp[i] 的时候,需要将[0, i] 分成两部分:
-
首先是离 i 最近的 [j, i],找到能满足是回文的 j,
-
再找 [0, j-1] 的最小分割次数,正是和状态表示一样,于是有
dp[i], [0, i] 是回文,0[0, i] 不是回文,有 0 < j <= i,[j, i] 是回文,求 min(dp[j]+1)[j, i] 不是回文,不考虑
-
🐎代码如下:
class Solution {
public:int minCut(string s) {int n = s.size();// 1. 预处理:子串是否是回文vector<vector<bool>> sub(n, vector<bool>(n));for(int i = n - 1; i >= 0; i--)for(int j = i; j < n; j++)if(s[i] == s[j])sub[i][j] = i+1 < j ? sub[i+1][j-1] : true;// 2. 分割,是另一个dp问题咯~vector<int> dp(n, 0x3f3f3f3f);for(int i = 0; i < n; i++){if(sub[0][i]) dp[i] = 0;elsefor(int j = 1; j <= i; j++)if(sub[j][i])dp[i] = min(dp[j - 1] + 1, dp[i]);}return dp[n-1];}
};
🥰如果本文对你有些帮助,欢迎👉 点赞 收藏 关注,你的支持是对作者大大莫大的鼓励!!(✿◡‿◡) 若有差错恳请留言指正~~
相关文章:

【算法】【动规】回文串系列问题
文章目录 跳转汇总链接3.1 回文子串3.2 最长回文子串3.3 分割回文串 IV3.4 分割回文串II(hard) 跳转汇总链接 👉🔗动态规划算法汇总链接 3.1 回文子串 🔗题目链接 给定一个字符串 s ,请计算这个字符串中有多少个回文子字符串。 …...

4-Docker命令之docker logs
1.docker logs介绍 docker logs命令是用来获取docker容器的日志 2.docker logs用法 docker logs [参数] CONTAINER [root@centos79 ~]# docker logs --helpUsage: docker logs [OPTIONS] CONTAINERFetch the logs of a containerAliases:docker container logs, docker lo…...

svelte基础语法学习
官网文档地址:绑定 / Each 块绑定 • Svelte 教程 | Svelte 中文网 1、样式 一般情况下父子组件内样式隔离、同级组件间样式隔离 2、页面布局 <style>P{color: red;} </stye><script> // 类似data let name ‘jiang’ let countVal 0 let s…...

Node.js教程-mysql模块
概述 在Node.js中,mysql模块是实现MySQL协议的JavaScript客户端工具。Node.js程序通过与MySQL建立链接,然后可对数据进行增、删、改、查等操作。 安装 由于mysql模块不是Node.js内置模块,需手动安装 npm i mysql注意:若MySQL服…...
网络通信协议
WebSocket通信 WebSocket是一种基于TCP的网络通信协议,提供了浏览器和服务器之间的全双工通信(full-duplex)能力。在WebSocket API中,浏览器和服务器只需要完成一次握手,两者之间就直接可以创建持久性的连接ÿ…...
Spark集群部署与架构
在大数据时代,处理海量数据需要分布式计算框架。Apache Spark作为一种强大的大数据处理工具,可以在集群中高效运行,处理数十TB甚至PB级别的数据。本文将介绍如何构建和管理Spark集群,以满足大规模数据处理的需求。 Spark集群架构…...
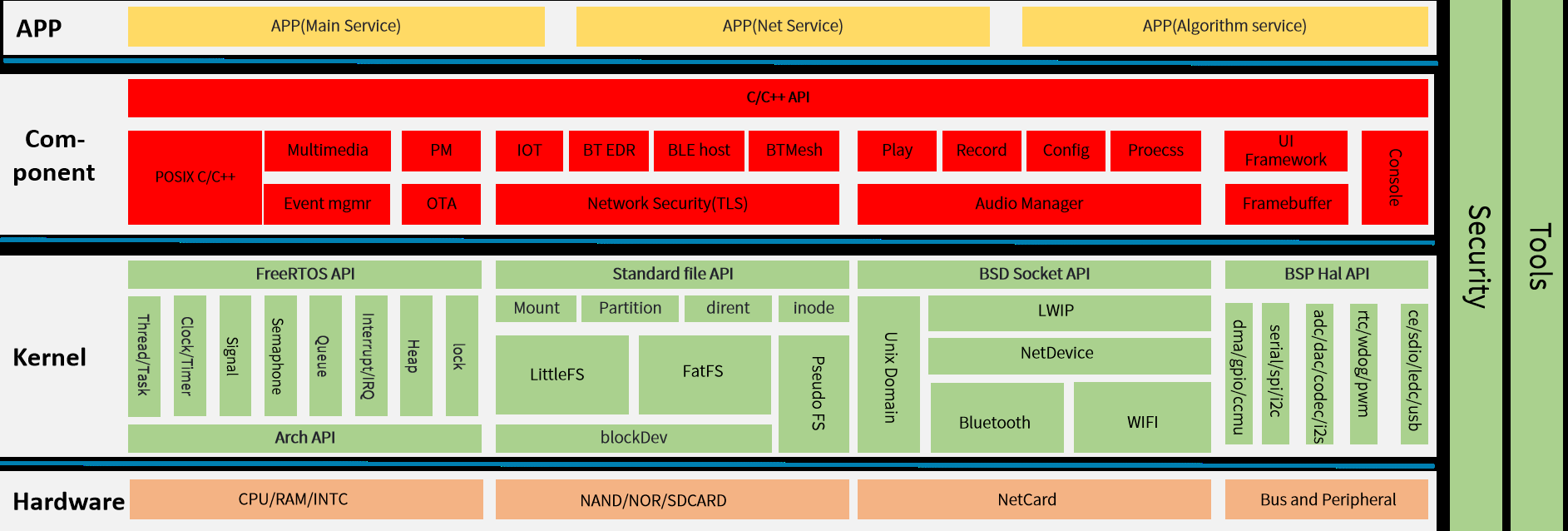
DshanMCU-R128s2 SDK 架构与目录结构
R128 S2 是全志提供的一款 M33(ARM)C906(RISCV-64)HIFI5(Xtensa) 三核异构 SoC,同时芯片内部 SIP 有 1M SRAM、8M LSPSRAM、8M HSPSRAM 以及 16M NORFLASH。 本文档作为 R128 FreeRTOS SDK 开发指南,旨在帮助软件开发工程师、技术支持工程师快速上手&am…...

【5G PHY】NR参考信号功率和小区总传输功率的计算
博主未授权任何人或组织机构转载博主任何原创文章,感谢各位对原创的支持! 博主链接 本人就职于国际知名终端厂商,负责modem芯片研发。 在5G早期负责终端数据业务层、核心网相关的开发工作,目前牵头6G算力网络技术标准研究。 博客…...

k8s学习 — 各知识点快捷入口
k8s学习 — 各知识点快捷入口 k8s学习 — 第一章 核心概念 k8s学习 — 第一章 核心概念 命名空间 实践: k8s学习 — (实践)第二章 搭建k8s集群k8s学习 — (实践)第三章 深入Podk8s学习 — (实践࿰…...

【Python】Python 批量转换PDF到Excel
PDF是面向展示和打印使用的,并未考虑编辑使用,所以缺少了很多编辑属性且非常难修改PDF里面的数据。当您需要分析或修改PDF文档数据时,可以将PDF保存为Excel工作簿,实现轻松编辑数据的需求。PDF转Excel,技术关键就是提取…...

Python并行计算和分布式任务全面指南
更多Python学习内容:ipengtao.com 大家好,我是彭涛,今天为大家分享 Python并行计算和分布式任务全面指南。全文2900字,阅读大约8分钟 并发编程是现代软件开发中不可或缺的一部分,它允许程序同时执行多个任务࿰…...

微信小程序promise封装
一. 在utils文件夹内创建一个request.js 写以下封装的 wx.request() 方法 const baseURL https:// 域名 ; //公用总路径地址 export const request (params) > { //暴露出去一个函数,并且接收一个外部传入的参数let dataObj params.data || {}; //…...

hash长度扩展攻击
作为一个信息安全的人,打各个学校的CTF比赛是比较重要的! 最近一个朋友发了道题目过来,发现有道题目比较有意思,这里跟大家分享下 这串代码的大致意思是: 这段代码首先引入了一个名为"flag.php"的文件&am…...
设计模式--命令模式
实验16:命令模式 本次实验属于模仿型实验,通过本次实验学生将掌握以下内容: 1、理解命令模式的动机,掌握该模式的结构; 2、能够利用命令模式解决实际问题。 [实验任务]:多次撤销和重复的命令模式 某系…...

单例模式的七种写法
为什么使用单例? 避免重复创建对象,节省内存,方便管理;一般我们在工具类中频繁使用单例模式; 1.饿汉式(静态常量)-[可用] /*** 饿汉式(静态常量)*/ public class Singleton1 {private static final Singleton1 INSTANCE new Singleton1();private Singleton1(){}…...
ElasticSearch入门介绍和实战
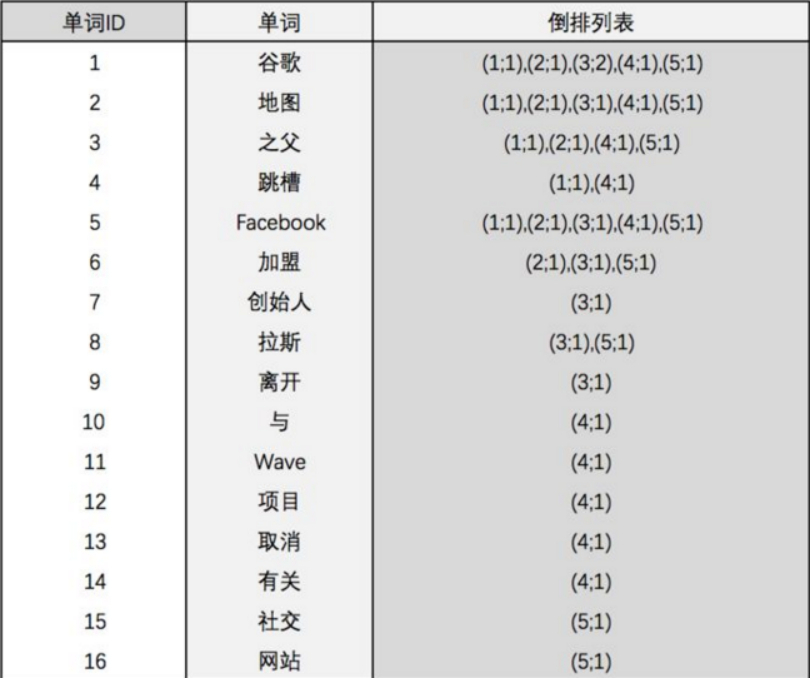
目录 1.ElasticSearch简介 1.1 ElasticSearch(简称ES) 1.2 ElasticSearch与Lucene的关系 1.3 哪些公司在使用Elasticsearch 1.4 ES vs Solr比较 1.4.1 ES vs Solr 检索速度 2. Lucene全文检索框架 2.1 什么是全文检索 2.2 分词原理之倒排索引…...

【FPGA】分享一些FPGA视频图像处理相关的书籍
在做FPGA工程师的这些年,买过好多书,也看过好多书,分享一下。 后续会慢慢的补充书评。 【FPGA】分享一些FPGA入门学习的书籍【FPGA】分享一些FPGA协同MATLAB开发的书籍 【FPGA】分享一些FPGA视频图像处理相关的书籍 【FPGA】分享一些FPGA高速…...
)
AUTOSAR从入门到精通-车载以太网(四)
目录 前言 原理 车载以太网发展历史 为何选择车载以太网...

MySQL报错:1054 - Unknown column ‘xx‘ in ‘field list的解决方法
我在操作MySQL遇到1054报错,报错内容:1054 - Unknown column Cindy in field list,下面演示解决方法,非常简单。 根据箭头指示,Cindy对应的应该是VARCHAR文本数字类型,字符串要用引号,所以解决方…...
:40+个依赖子模块之ActionBarShadow)
【Android 13】使用Android Studio调试系统应用之Settings移植(四):40+个依赖子模块之ActionBarShadow
文章目录 一、篇头二、系列文章2.1 Android 13 系列文章2.2 Android 9 系列文章2.3 Android 11 系列文章三、子模块AS移植3.1 AS创建目标3.2 创建ActionBarShadow(1)使用VS Code打开org_settings/SettingsLib目录(2)ActionBarShadow的Manifest.xml(3)ActionBarShadow的An…...
)
云计算——弹性云计算器(ECS)
弹性云服务器:ECS 概述 云计算重构了ICT系统,云计算平台厂商推出使得厂家能够主要关注应用管理而非平台管理的云平台,包含如下主要概念。 ECS(Elastic Cloud Server):即弹性云服务器,是云计算…...
)
rknn优化教程(二)
文章目录 1. 前述2. 三方库的封装2.1 xrepo中的库2.2 xrepo之外的库2.2.1 opencv2.2.2 rknnrt2.2.3 spdlog 3. rknn_engine库 1. 前述 OK,开始写第二篇的内容了。这篇博客主要能写一下: 如何给一些三方库按照xmake方式进行封装,供调用如何按…...

3.3.1_1 检错编码(奇偶校验码)
从这节课开始,我们会探讨数据链路层的差错控制功能,差错控制功能的主要目标是要发现并且解决一个帧内部的位错误,我们需要使用特殊的编码技术去发现帧内部的位错误,当我们发现位错误之后,通常来说有两种解决方案。第一…...

如何在看板中体现优先级变化
在看板中有效体现优先级变化的关键措施包括:采用颜色或标签标识优先级、设置任务排序规则、使用独立的优先级列或泳道、结合自动化规则同步优先级变化、建立定期的优先级审查流程。其中,设置任务排序规则尤其重要,因为它让看板视觉上直观地体…...

ssc377d修改flash分区大小
1、flash的分区默认分配16M、 / # df -h Filesystem Size Used Available Use% Mounted on /dev/root 1.9M 1.9M 0 100% / /dev/mtdblock4 3.0M...

CRMEB 框架中 PHP 上传扩展开发:涵盖本地上传及阿里云 OSS、腾讯云 COS、七牛云
目前已有本地上传、阿里云OSS上传、腾讯云COS上传、七牛云上传扩展 扩展入口文件 文件目录 crmeb\services\upload\Upload.php namespace crmeb\services\upload;use crmeb\basic\BaseManager; use think\facade\Config;/*** Class Upload* package crmeb\services\upload* …...

第 86 场周赛:矩阵中的幻方、钥匙和房间、将数组拆分成斐波那契序列、猜猜这个单词
Q1、[中等] 矩阵中的幻方 1、题目描述 3 x 3 的幻方是一个填充有 从 1 到 9 的不同数字的 3 x 3 矩阵,其中每行,每列以及两条对角线上的各数之和都相等。 给定一个由整数组成的row x col 的 grid,其中有多少个 3 3 的 “幻方” 子矩阵&am…...

MySQL用户和授权
开放MySQL白名单 可以通过iptables-save命令确认对应客户端ip是否可以访问MySQL服务: test: # iptables-save | grep 3306 -A mp_srv_whitelist -s 172.16.14.102/32 -p tcp -m tcp --dport 3306 -j ACCEPT -A mp_srv_whitelist -s 172.16.4.16/32 -p tcp -m tcp -…...

MySQL账号权限管理指南:安全创建账户与精细授权技巧
在MySQL数据库管理中,合理创建用户账号并分配精确权限是保障数据安全的核心环节。直接使用root账号进行所有操作不仅危险且难以审计操作行为。今天我们来全面解析MySQL账号创建与权限分配的专业方法。 一、为何需要创建独立账号? 最小权限原则…...

浪潮交换机配置track检测实现高速公路收费网络主备切换NQA
浪潮交换机track配置 项目背景高速网络拓扑网络情况分析通信线路收费网络路由 收费汇聚交换机相应配置收费汇聚track配置 项目背景 在实施省内一条高速公路时遇到的需求,本次涉及的主要是收费汇聚交换机的配置,浪潮网络设备在高速项目很少,通…...
