Nature | 大型语言模型(LLM)能够产生和发现新知识吗?
大型语言模型(LLM)是基于大量数据进行预训练的超大型深度学习模型。底层转换器是一组神经网络,这些神经网络由具有自注意力功能的编码器和解码器组成。编码器和解码器从一系列文本中提取含义,并理解其中的单词和短语之间的关系。通过此过程,转换器可学会理解基本的语法、语言和知识。
借助转换器神经网络架构,人们可以使用非常大规模的模型,其中通常具有数千亿个参数。这种大规模模型可以摄取通常来自互联网的大量数据,但也可以从包含 500 多亿个网页的 Common Crawl 和拥有约 5700 万个页面的 Wikipedia 等来源摄取数据。
一般来讲,LLM主要是在已有的知识库上进行学习,然后通过阅读、理解、写作和编码来帮助人们解决问题。但是,一个根本性的问题是,LLM能发现并产生全新的知识吗?
最近,来自 Google DeepMind 的研究团队提出了一种为数学和计算机科学问题搜索解决方案的新方法 ——FunSearch。FunSearch 的工作原理是将预训练的 LLM(以计算机代码的形式提供创造性解决方案)与自动「评估器」配对,以防止产生幻觉和错误思路。通过在这两个组件之间来回迭代,最初的解决方案演变成了「新的知识」。相关论文发表在最近一期的《Nature》杂志上。

这项工作是首次利用 LLM 在科学或数学的挑战性开放问题方面取得新发现。
FunSearch 发现了 cap set 问题的全新解决方案,这是数学中一个长期存在的开放问题。此外,为了展示 FunSearch 的实际用途,DeepMind 还用它来发现更有效的算法来解决「装箱」问题,该问题应用广泛,比如可以用于提高数据中心的效率。
研究团队认为 FunSearch 将成为一个特别强大的科学工具,因为它输出的程序揭示了其解决方案是如何构建的,而不仅仅是解决方案是什么。这将会激发科学家的进一步见解,从而形成科学改进与发现的良性循环。
找到NP-hard问题更优解法
DeepMind具体展示了两类问题,它们都属于NP-hard问题。在学界看来,没有而且可能永远也不会有一种算法能在所有情况下都在多项式时间内找到NP-hard问题的精确解。面对这样的问题,研究者通常会寻找近似解或适用于特定情况的有效算法。
Cap set问题
具体到FunSearch,它解决的第一类NP-hard问题是Cap set问题,是上限集问题的一种,它的描述是这样的:
"在一个n维空间中的每个维度上都有等距的n个点(共n^n个,比如3维就是3*3*3),从中找出尽可能多的点构成一个集合,要求集合中任选3个点均不共线,这样的集合中最多有多少个点?"

如果看上去有些难以理解,不妨再了解一下Cap set问题的前身——上世纪70年代遗传学家Marsha Falco发明的一套卡牌游戏。
这套卡牌游戏中一共有81张牌,每张牌中都有1至3个颜色图案,同一张牌中的图案颜色、形状和阴影完都全相同。
这套牌一共有3种颜色、3种形状和3种阴影,加上图案数量的不同,一共有3*3*3*3=81张,玩家需要翻开一些纸牌,找到3张牌的特殊组合。

如果把这种“特殊组合”的具体方式用离散几何形式进行表达,就得到了Cap set问题。Cap set问题同样诞生于70年代,由牛津大学数学家Ron Graham提出,而第一个重要结果直到90年代才出现。
2007年,陶哲轩在一篇博客文章中曾提到,这是他最喜欢的开放式数学问题。
在FunSearch出现之前,Cap set问题最重大的突破是美国数学家Jordan Ellenberg和荷兰数学家Dion Gijswijt于2016年提出的。
通过多项式方法,Ellenberg和Gijswijt将n>6时(n≤6时可精确找到最大集合)此类问题解的上确界缩小到了2.756^n。同样在n>6时,下确界的较新数字则是2.218^n,由布里斯托大学博士生Fred Tyrrell在2022年提出。但这个下确界仅仅存在于理论上——当n=8时,人类能构建出的最大集合中只有496个点,而按照Tyrrell的结论,点的数量应不少于585.7个。
FunSearch则将集合规模扩大到了512个点——虽然和理论值依旧存在差距,但仍被视为20年来在此问题上最重大的突破。同时,Cap set集合大小的下确界也被FunSearch提高到了2.2202^n。

在线装箱问题
第二类是在线装箱问题:
假设有一组容量为C的标准集装箱和n个物品序列(物品大小不超过C),这些物品按一定顺序到达。“在线”是指操作者无法事先看到所有的物品,但必须在物品到达时立刻决定将物品装入哪个集装箱。最终的目标,是使所用集装箱数量尽可能小。
在线装箱问题引起广泛研究是从上世纪70年代开始的,最早更是可以追溯到1831年高斯所研究的布局问题。经过近200年的研究,仍然没有成熟的理论和有效的数值计算方法。
传统上常用的贪心算法包括First Fit和Best Fit两种:
- First Fit是指将每个物品放入第一个能容纳它的箱子中。
- Best Fit则是将每个物品放入能容纳它的且箱子中剩余空间最小的箱子。

而FunSearch则提出了新的算法,该算法在OR和Weibull两个测试数据集中,所用集装箱的数量均大幅下降。特别是在当测试集物品数目达到10万时,FunSearch找到的方案,消耗集装箱数量只比理论下界多出了0.03%。
通过语言模型的进化推动发现
FunSearch 采用由 LLM 支持的进化方法,鼓励并推动得分最高的思路想法。这些想法被表达成计算机程序,以便它们可以自动运行和评估。
首先,用户需要以代码的形式编写问题的描述。该描述包括评估程序的过程和用于初始化程序池的种子程序。
FunSearch 是一个迭代过程,在每次迭代中,系统都会从当前的程序池中选择一些程序,并将其馈送到 LLM。LLM 创造性地在此基础上进行构建,生成新的程序,并自动进行评估。最好的程序将被添加回现有程序库中,从而创建一个自我改进的循环。FunSearch 使用 Google 的 PaLM 2,但对其他接受过代码训练的方法兼容。
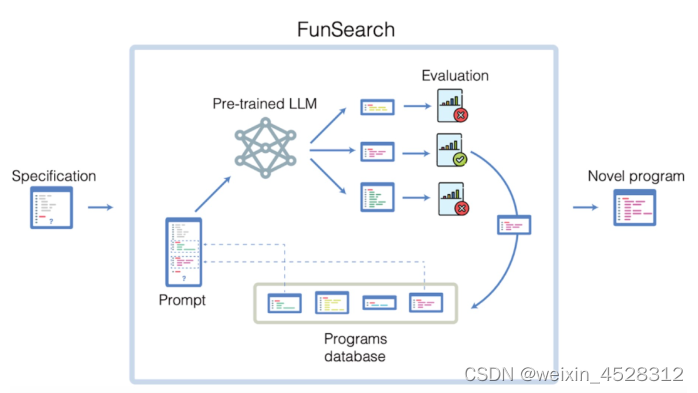
图一:LLM 会从程序数据库中检索出生成的最佳程序,并被要求生成一个更好的程序。
众所周知,在不同领域发现新的数学知识和算法是一项艰巨的任务,很大程度上超出了当前最先进人工智能系统的能力。为了让 FunSearch 做到这一点,该研究引入了多个关键组件。FunSearch 不是从头开始,而是从关于问题的常识开始一个进化过程,让 FunSearch 专注于寻找最关键的想法以获得新的发现。
此外,FunSearch 的进化过程使用一种策略来提高想法的多样性,以避免出现停滞情况。最后,为了提高系统效率,进化过程是并行运行的。
在数学领域开辟新天地
DeepMind 表示,他们首先要解决的是 Cap set 问题,这是一个开放性难题,几十年来一直困扰着多个研究领域的数学家。知名数学家陶哲轩曾把它描述为自己最喜欢的开放性问题。DeepMind 选择与威斯康星大学麦迪逊分校的数学教授 Jordan Ellenberg 合作,他是 Cap set 问题的重要突破者。
这个问题包括在一个高维网格中找到最大的点集(称为 cap set),其中没有三个点位于一条直线上。这个问题之所以重要,是因为它可以作为极值组合学中其他问题的模型。极值组合学研究的是数字、图或其他对象的集合可能有多大或多小。暴力破解方法无法解决这个问题 —— 要考虑的可能性数量很快就会超过宇宙中原子的数量。
FunSearch 以程序形式生成的解决方案在某些情况下发现了有史以来最大的 cap set。这代表了过去 20 年中 cap set 规模的最大增长。此外,FunSearch 的性能超过了最先进的计算求解器,因为这个问题的规模远远超出了它们目前的能力。
这些结果表明,FunSearch 技术可以让人类超越困难组合问题的既定结果,而在这些问题上很难建立直觉。DeepMind 期望这种方法能够在组合学中类似理论问题的新发现中发挥作用,并在未来为通信理论等领域带来新的可能性。

图二:交互式图表显示了从种子程序(上)到新的高分函数(下)的演变。每个圆圈都代表一个程序,其大小与分配给它的分数成正比。图中仅显示底部程序的上级。FunSearch 为每个节点生成的相应函数如右侧所示。
FunSearch 偏好简洁、可由人类理解的程序
尽管发现新的数学知识本身意义重大,但与传统的计算机搜索技术相比,FunSearch 方法还展现出了其他的优势。这是因为,FunSearch 并不是一个只会生成问题解决方案的黑箱。相反,它生成的程序会描述出这些解决方案是如何得出的。这种「show-your-working」通常是科学家的工作方式,他们通过阐述产生新发现或新现象的过程来解释这些发现或现象。
FunSearch 更倾向于寻找高度紧凑的程序所代表的解决方案,即具有较低 Kolmogorov 复杂度的解决方案(Kolmogorov 复杂度是输出解的最短计算机程序的长度)。简短的程序可以描述非常大的对象,从而使 FunSearch 能够扩展到非常复杂的问题。此外,这也让研究人员更容易理解 FunSearch 的程序输出。Ellenberg 说:「FunSearch 为制定攻击策略提供了一种全新的机制。FunSearch 生成的解决方案在概念上要比单纯的数字列表丰富得多。当我研究它们时,我学到了一些东西。」
更重要的是,FunSearch 程序的这种可解释性可以为研究人员提供可操作的见解。例如,DeepMind 在使用 FunSearch 的过程中注意到,它的一些高分输出的代码中存在耐人寻味的对称性。这让 DeepMind 对问题有了新的认识,他们利用这种认识改进了引入 FunSearch 的问题,从而找到了更好的解决方案。DeepMind 认为,这是人类与 FunSearch 在数学领域的许多问题上进行合作的典范。

图三:左:通过检查 FunSearch 生成的代码,DeepMind 获得了更多可操作的见解(高亮部分)。右:使用(更短的)左图程序构造的原始「可接受」集合。
解决一个众所周知的计算难题
在理论 cap set 问题取得成功的鼓舞下,DeepMind 决定将 FunSearch 应用于计算机科学中一个重要的实际挑战 —— 装箱问题(bin packing),以探索它的灵活性。装箱问题关注的是如何将不同尺寸的物品打包到最少数量的箱子中。它是许多现实世界问题的核心,从装载物品的集装箱到数据中心的计算工作分配,这些场景都需要最大限度地降低成本。
在线装箱问题通常使用基于人类经验的算法规则(启发式)来解决。但是,要为每种特定情况(大小、时间或容量各不相同)找到一套规则是非常具有挑战性的。尽管与 cap set 问题非常不同,但为这个问题设置 FunSearch 很容易。FunSearch 提供了一个自动定制的程序(适应数据的具体情况),优于现有的启发式方法 —— 可以使用更少的箱子来打包相同数量的物品。
像在线装箱这样的复杂组合问题可以使用其他人工智能方法来解决,比如神经网络和强化学习。这些方法也被证明是有效的,但也可能需要大量的资源来部署。另一方面,FunSearch 输出的代码易于检查和部署,这意味着它的解决方案有可能被应用到各种现实工业系统中,从而迅速带来效益。

图四:使用现有启发式 ——Best-fit 启发式(左)和 FunSearch 发现的启发式(右)进行装箱的示例。
总结
整体上看,FunSearch的工作流程是一个迭代过程,核心是搜索能解决问题的程序,而不是问题答案本身。搜索,正是DeepMind自AlphaGo以来一直坚持探索的路线。作者之一、谷歌DeepMind研究副总裁Pushmeet Kohli表示:训练数据中不会有这个方案,它之前甚至根本不为人类所知。
FunSearch也表明,如果我们限制好LLM的幻觉,不仅可以用来产生新的数学发现,还可以提出解决实际世界问题的创新解决方案。此外FunSearch预示了未来LLM驱动的方法将在科学和工业领域广泛应用,主助理于解决紧迫的科学和工程挑战。
FunSearch 证明,如果能防止 LLM 产生幻觉,那么这些模型的力量不仅可以用来产生新的数学发现,还可以用来揭示重要现实问题的潜在解决方案。
DeepMind 认为,对于科学和工业领域的许多问题 —— 无论是长期存在的问题还是新问题 —— 使用 LLM 驱动的方法生成有效和量身定制的算法将成为普遍做法。
其实,这仅仅是一个开始。随着 LLM 不断取得进展,FunSearch 也将不断完善。DeepMind 表示,他们还将努力扩展其功能,以应对社会上各种紧迫的科学和工程挑战。
FunSearch之所以强大是因为它输出的不仅仅是解决方案,它还能展示解决方案是怎么来的。这就像是给你看一个解谜过程,让你明白答案是怎么得出的。它喜欢找那些既简洁又能搞定复杂问题的方案。
FunSearch找到的答案不只是一串数字那么简单,它还能给科学家们提供新的视角。比如通过描述理解程序是如何工作的,科学家们可能会发现问题中的新模式,这可以激发科学家使用FunSearch进行进一步的洞察,推动改进、发现的良性循环。
参考文献
(1) https://www.nature.com/articles/s41586-023-06924-6
(2) https://deepmind.google/discover/blog/funsearch-making-new-discoveries-in-mathematical-sciences-using-large-language-models/
相关文章:

Nature | 大型语言模型(LLM)能够产生和发现新知识吗?
大型语言模型(LLM)是基于大量数据进行预训练的超大型深度学习模型。底层转换器是一组神经网络,这些神经网络由具有自注意力功能的编码器和解码器组成。编码器和解码器从一系列文本中提取含义,并理解其中的单词和短语之间的关系。通…...
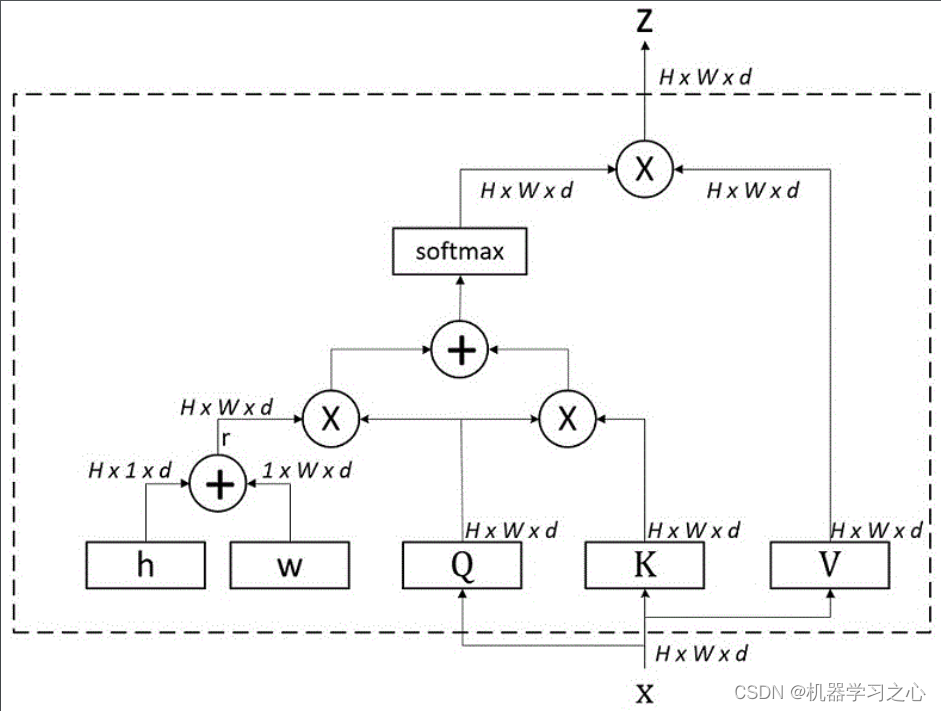
多维时序 | MATLAB实CNN-Mutilhead-Attention卷积神经网络融合多头注意力机制多变量时间序列预测
多维时序 | MATLAB实CNN-Mutilhead-Attention卷积神经网络融合多头注意力机制多变量时间序列预测 目录 多维时序 | MATLAB实CNN-Mutilhead-Attention卷积神经网络融合多头注意力机制多变量时间序列预测预测效果基本介绍模型描述程序设计参考资料 预测效果 基本介绍 多维时序 | …...
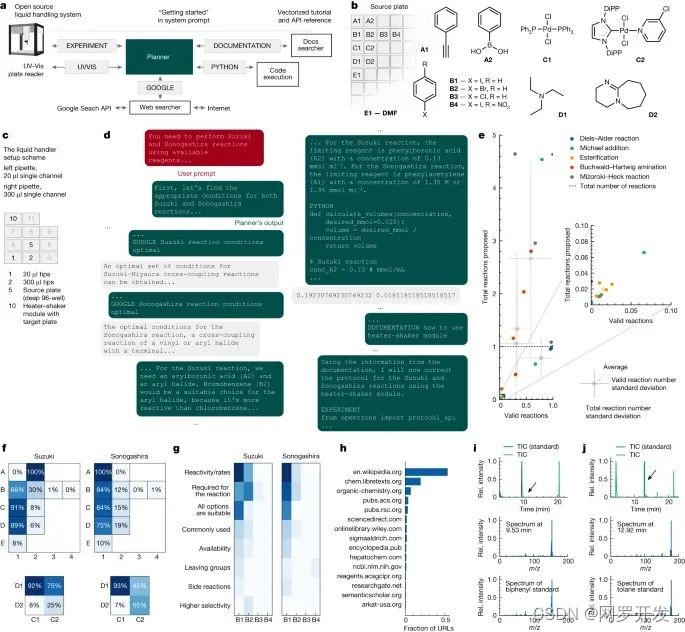
Nature 新研究发布,GPT 驱动的机器人化学家能够自行设计和进行实验,这对科研意味着什么?
文章目录 前言揭秘Coscientist不到四分钟,设计并改进了程序能力越大,责任越大 前言 有消息称,AI 大模型 “化学家” 登 Nature 能够自制阿司匹林、对乙酰氨基酚、布洛芬,甚至连复杂的钯催化交叉偶联反应,也能完成。 …...
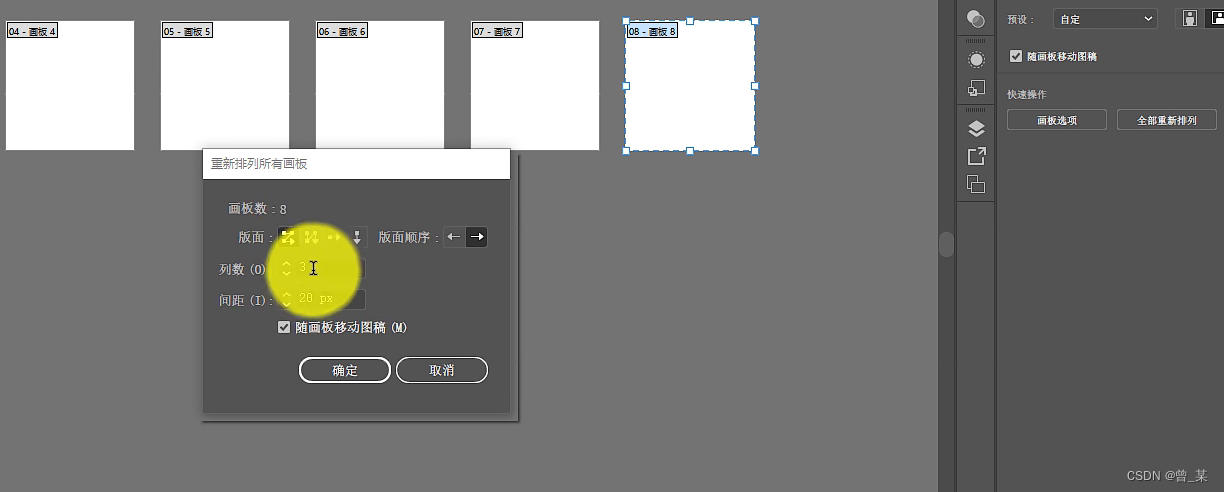
Ai画板原理
在创建时画板可以选择数量和排列方式 也可以采用这个图片左上的画板工具,选择画板在其他地方画框即可生成,同时可以在属性框中可以修改尺寸大小 选择全部重新排列可以进行创建时的布局...

【hacker送书第11期】Python数据分析从入门到精通
探索数据世界,揭示未来趋势 《Python数据分析从入门到精通》是你掌握Python数据分析的理想选择。本书深入讲解核心工具如pandas、matplotlib和numpy,助您轻松处理和理解复杂数据。 通过matplotlib、seaborn和创新的pyecharts,本书呈现生动直…...
)
华为OD机试 - 精准核酸检测(Java JS Python C)
在线OJ刷题 题目详情 - 精准核酸检测 - Hydro 题目描述 为了达到新冠疫情精准防控的需要,为了避免全员核酸检测带来的浪费,需要精准圈定可能被感染的人群。 现在根据传染病流调以及大数据分析,得到了每个人之间在时间、空间上是否存在轨迹交叉。 现在给定一组确诊人员编…...

智能优化算法应用:基于材料生成算法3D无线传感器网络(WSN)覆盖优化 - 附代码
智能优化算法应用:基于材料生成算法3D无线传感器网络(WSN)覆盖优化 - 附代码 文章目录 智能优化算法应用:基于材料生成算法3D无线传感器网络(WSN)覆盖优化 - 附代码1.无线传感网络节点模型2.覆盖数学模型及分析3.材料生成算法4.实验参数设定5.算法结果6.…...

【MySQL】:超详细MySQL完整安装和配置教程
🎥 屿小夏 : 个人主页 🔥个人专栏 : MySQL从入门到进阶 🌄 莫道桑榆晚,为霞尚满天! 文章目录 📑前言一. MySQL数据库1.1 版本1.2 下载1.3 安装1.4 客户端连接 🌤️全篇总…...

OpenAI亲授ChatGPT “屠龙术”!官方Prompt 工程指南来啦
应该如何形容 Prompt 工程呢?对于一个最开始使用 ChatGPT 的新人小白,面对据说参数量千亿万亿的庞然巨兽,Prompt 神秘的似乎像某种献祭:我扔进去几句话,等待聊天窗口后的“智慧生命”给我以神谕。 然而,上…...
最新ChatGPT商业运营网站程序源码,支持Midjourney绘画,GPT语音对话+DALL-E3文生图+文档对话总结
一、前言 SparkAi创作系统是基于ChatGPT进行开发的Ai智能问答系统和Midjourney绘画系统,支持OpenAI-GPT全模型国内AI全模型。本期针对源码系统整体测试下来非常完美,可以说SparkAi是目前国内一款的ChatGPT对接OpenAI软件系统。那么如何搭建部署AI创作Ch…...

经验 | IDEA常用快捷键
1、编辑(Editing) Ctrl Space 基本的代码完成(类、方法、属性) Ctrl Alt Space 快速导入任意类 Ctrl Shift Enter 语句完成 Ctrl P 参数信息(在方法中调用参数) Ctrl Q 快速查看文档 Shift F…...

spark中 write.csv时, 添加第一行的标题title
在 Spark 中使用 write.csv 写入 CSV 文件时,默认情况下是不会在文件中添加标题行的。但是,你可以通过设置 header 选项来控制是否包含标题行。 下面是一个示例: val data Seq((1, "John", 28),(2, "Alice", 22),(3, …...

HTML美化网页
使用CSS3美化的原因 用css美化页面文本,使页面漂亮、美观、吸引用户 可以更好的突出页面的主题内容,使用户第一眼可以看到页面主要内容 具有良好的用户体验 <span>标签 作用 能让某几个文字或者某个词语凸显出来 有效的传递页面信息用css美化页面文本,使页面漂…...
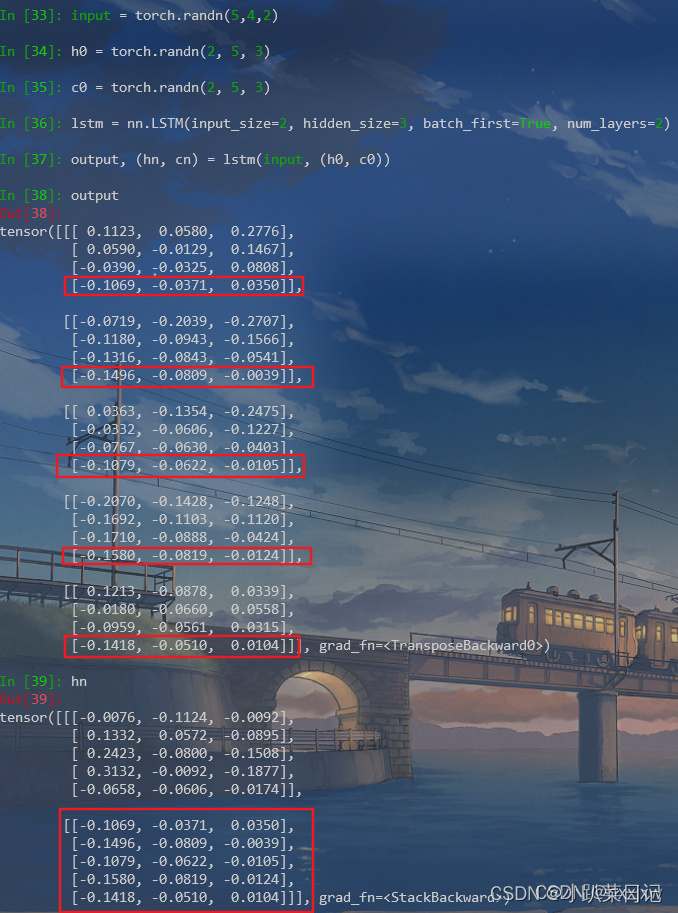
nn.LSTM个人记录
简介 nn.LSTM参数 torch.nn.lstm(input_size, "输入的嵌入向量维度,例如每个单词用50维向量表示,input_size就是50"hidden_size, "隐藏层节点数量,也是输出的嵌入向量维度"num_layers, "lstm 隐层的层数,默认…...

vr虚拟高压电器三维仿真展示更立体全面
VR工业虚拟仿真软件的应用价值主要体现在以下几个方面: 降低成本:通过VR技术进行产品设计和开发,可以在虚拟环境中进行,从而减少对物理样机的依赖,降低试错成本和时间。此外,利用VR技术构建的模拟场景使用方…...

轮廓平滑方法
目录 1. 形态学操作 2. 边缘平滑化 3. 轮廓近似 python 有回归线平滑 2D 轮廓 1. 形态学操作 利用形态学操作(例如腐蚀、膨胀、开运算、闭运算等)可以使分割边界更加平滑和连续。腐蚀可以消除小的不连续区域,膨胀可以填充空洞࿰…...
十大VSCODE 插件推荐2023
1、海鲸AI 插件链接:ChatGPT GPT-4 - 海鲸AI - Visual Studio Marketplace 包含了ChatGPT(3.5/4.0)等多个AI模型。可以实现代码优化,代码解读,代码bug修复等功能,反应迅捷,体验出色,是一个多功能的AI插件…...

HBase 集群搭建
文章目录 安装前准备兼容性官方网址 集群搭建搭建 Hadoop 集群搭建 Zookeeper 集群解压缩安装配置文件高可用配置分发 HBase 文件 服务的启停启动顺序停止顺序 验证进程查看 Web 端页面 安装前准备 兼容性 1)与 Zookeeper 的兼容性问题,越新越好&#…...
大三了,C++还算可以从事什么岗位比较好?
大三了,C还算可以从事什么岗位比较好? 在开始前我有一些资料,是我根据自己从业十年经验,熬夜搞了几个通宵,精心整理了一份「c的资料从专业入门到高级教程工具包」,点个关注,全部无偿共享给大家…...

java 贪吃蛇游戏
前言 此实现较为简陋,如有错误请指正。 其次代码中的图片需要自行添加地址并修改。 主类 public class Main { public static void main(String[] args) { new myGame(); } } 1 2 3 4 5 游戏类 import javax.swing.*; import java.awt.eve…...

Python爬虫实战:研究MechanicalSoup库相关技术
一、MechanicalSoup 库概述 1.1 库简介 MechanicalSoup 是一个 Python 库,专为自动化交互网站而设计。它结合了 requests 的 HTTP 请求能力和 BeautifulSoup 的 HTML 解析能力,提供了直观的 API,让我们可以像人类用户一样浏览网页、填写表单和提交请求。 1.2 主要功能特点…...

零门槛NAS搭建:WinNAS如何让普通电脑秒变私有云?
一、核心优势:专为Windows用户设计的极简NAS WinNAS由深圳耘想存储科技开发,是一款收费低廉但功能全面的Windows NAS工具,主打“无学习成本部署” 。与其他NAS软件相比,其优势在于: 无需硬件改造:将任意W…...

黑马Mybatis
Mybatis 表现层:页面展示 业务层:逻辑处理 持久层:持久数据化保存 在这里插入图片描述 Mybatis快速入门 
2025 后端自学UNIAPP【项目实战:旅游项目】6、我的收藏页面
代码框架视图 1、先添加一个获取收藏景点的列表请求 【在文件my_api.js文件中添加】 // 引入公共的请求封装 import http from ./my_http.js// 登录接口(适配服务端返回 Token) export const login async (code, avatar) > {const res await http…...

新能源汽车智慧充电桩管理方案:新能源充电桩散热问题及消防安全监管方案
随着新能源汽车的快速普及,充电桩作为核心配套设施,其安全性与可靠性备受关注。然而,在高温、高负荷运行环境下,充电桩的散热问题与消防安全隐患日益凸显,成为制约行业发展的关键瓶颈。 如何通过智慧化管理手段优化散…...

反射获取方法和属性
Java反射获取方法 在Java中,反射(Reflection)是一种强大的机制,允许程序在运行时访问和操作类的内部属性和方法。通过反射,可以动态地创建对象、调用方法、改变属性值,这在很多Java框架中如Spring和Hiberna…...

基于SpringBoot在线拍卖系统的设计和实现
摘 要 随着社会的发展,社会的各行各业都在利用信息化时代的优势。计算机的优势和普及使得各种信息系统的开发成为必需。 在线拍卖系统,主要的模块包括管理员;首页、个人中心、用户管理、商品类型管理、拍卖商品管理、历史竞拍管理、竞拍订单…...

Redis:现代应用开发的高效内存数据存储利器
一、Redis的起源与发展 Redis最初由意大利程序员Salvatore Sanfilippo在2009年开发,其初衷是为了满足他自己的一个项目需求,即需要一个高性能的键值存储系统来解决传统数据库在高并发场景下的性能瓶颈。随着项目的开源,Redis凭借其简单易用、…...

Python Einops库:深度学习中的张量操作革命
Einops(爱因斯坦操作库)就像给张量操作戴上了一副"语义眼镜"——让你用人类能理解的方式告诉计算机如何操作多维数组。这个基于爱因斯坦求和约定的库,用类似自然语言的表达式替代了晦涩的API调用,彻底改变了深度学习工程…...

提升移动端网页调试效率:WebDebugX 与常见工具组合实践
在日常移动端开发中,网页调试始终是一个高频但又极具挑战的环节。尤其在面对 iOS 与 Android 的混合技术栈、各种设备差异化行为时,开发者迫切需要一套高效、可靠且跨平台的调试方案。过去,我们或多或少使用过 Chrome DevTools、Remote Debug…...
