QAM 归一化因子
文章目录
- 前言
- 一、归一化
- 1、作用
- 2、OFDM 归一化因子
- 二、归一化因子公式
前言
在做通信系统仿真时,遇到了 QAM 归一化因子的求解,对这里不是很清楚,因此本文对 QAM(正交振幅调制)归一化因子学习做了一下记录。
一、归一化
1、作用
将功率(能量)进行归一化处理。添加功率归一化因子,目的在于使得不同调制方式(或者说对于所有映射方式)都能够取得相同的平均功率。
2、OFDM 归一化因子
在 OFDM 系统中,归一化因子是一个重要的参数,它对信号的传输质量和干扰抑制能力起着关键作用。
归一化因子是指在 OFDM 信号中,每个子载波上的信号功率之和与总的发射功率之间的比值。在 OFDM 系统中,将数据流分成多个子载波进行传输,每个子载波上携带一部分数据。归一化因子的作用是使得每个子载波上的平均功率相等,从而保证在各个子载波上的信号能够以相同的能量水平进行传输。
在 OFDM 系统中,归一化因子的计算方法通常是通过将各个子载波的信号功率相加,然后除以总的发射功率。这样可以保证每个子载波上的平均功率相等,从而避免了某些子载波上信号功率过大或过小的问题。归一化因子的大小直接影响到每个子载波上的信号传输质量,因此在设计 OFDM 系统时需要合理选择归一化因子的数值
归一化能量的 4QAM~256QAM 如下图所示:
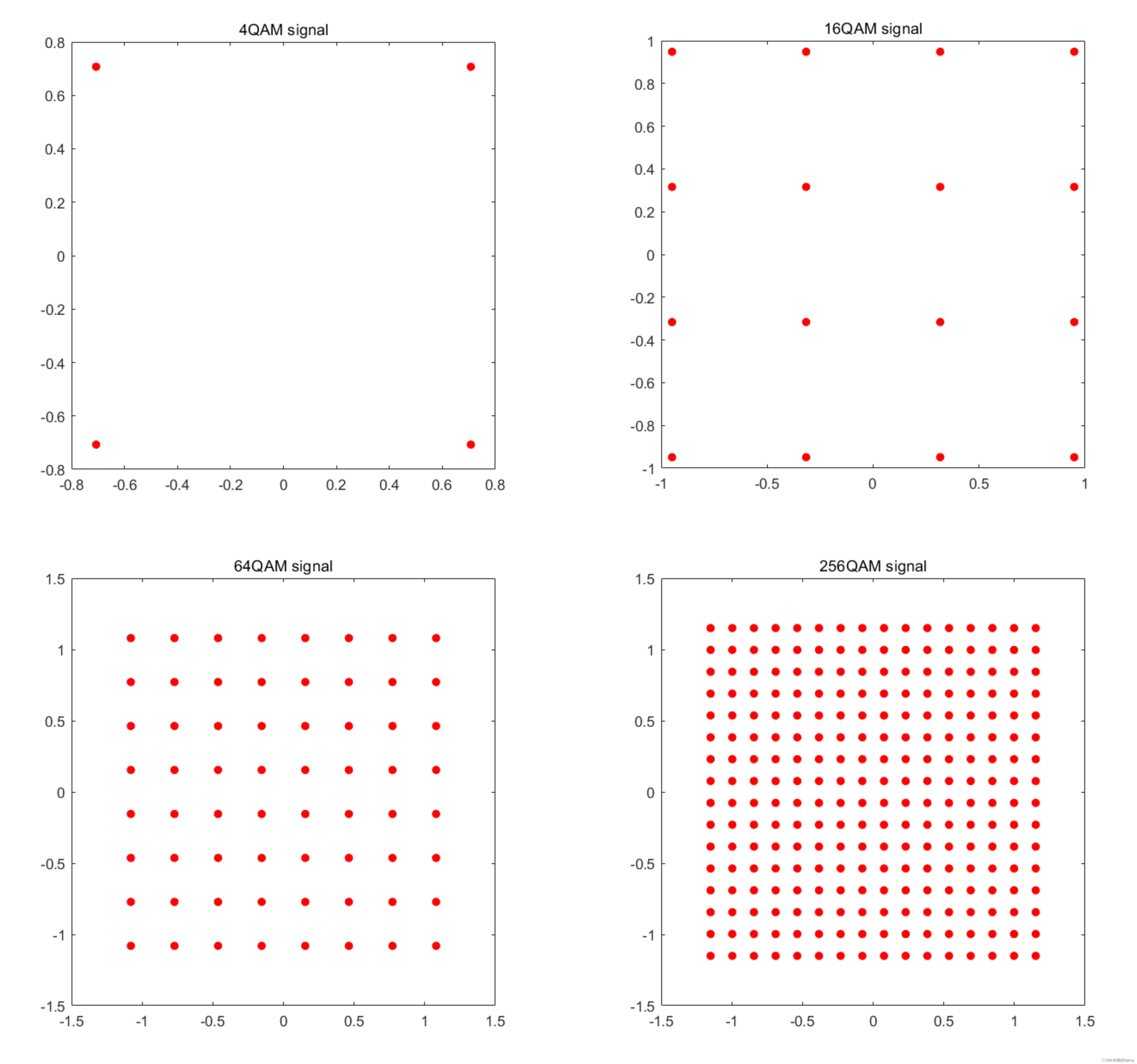
二、归一化因子公式
μ = 3 2 E s M − 1 \mu = \sqrt{\frac{3}{2}\frac{E_s}{M-1}} μ=23M−1Es
- μ \mu μ:归一化因子
- M M M:调制阶数
- E s E_s Es:每个符号的平均能量
b = 4; % 每一 QAM 符号的比特数
M = 2^b; % 调制阶数
Es = 1; % 每个符号的平均能量
A = sqrt(3/2/(M-1)*Es); % M-QAM 归一化因子
因此:
- 16 QAM归一化因子为: μ = 1 10 \mu=\frac{1}{\sqrt{10}} μ=101
- 64 QAM归一化因子为: μ = 1 42 \mu=\frac{1}{\sqrt{42}} μ=421
- 256 QAM归一化因子为: μ = 1 170 \mu=\frac{1}{\sqrt{170}} μ=1701
有关不同阶 QAM 调制星座图中,符号能量的归一化计算原理可以参考:不同阶QAM调制星座图中,符号能量的归一化计算原理
我的qq:2442391036,欢迎交流!
相关文章:

QAM 归一化因子
文章目录 前言一、归一化1、作用2、OFDM 归一化因子 二、归一化因子公式 前言 在做通信系统仿真时,遇到了 QAM 归一化因子的求解,对这里不是很清楚,因此本文对 QAM(正交振幅调制)归一化因子学习做了一下记录。 一、归…...

PoE交换机传输距离是多少?100米?250米?
你们好,我的网工朋友。 今天和你聊聊PoE交换机,之前有系统地给你讲解过一篇,可以先回顾一下哈:《啥样的交换机才叫高级交换机?这张图告诉你》 为什么都说PoE交换机好?它最显著的特点就是: 可…...
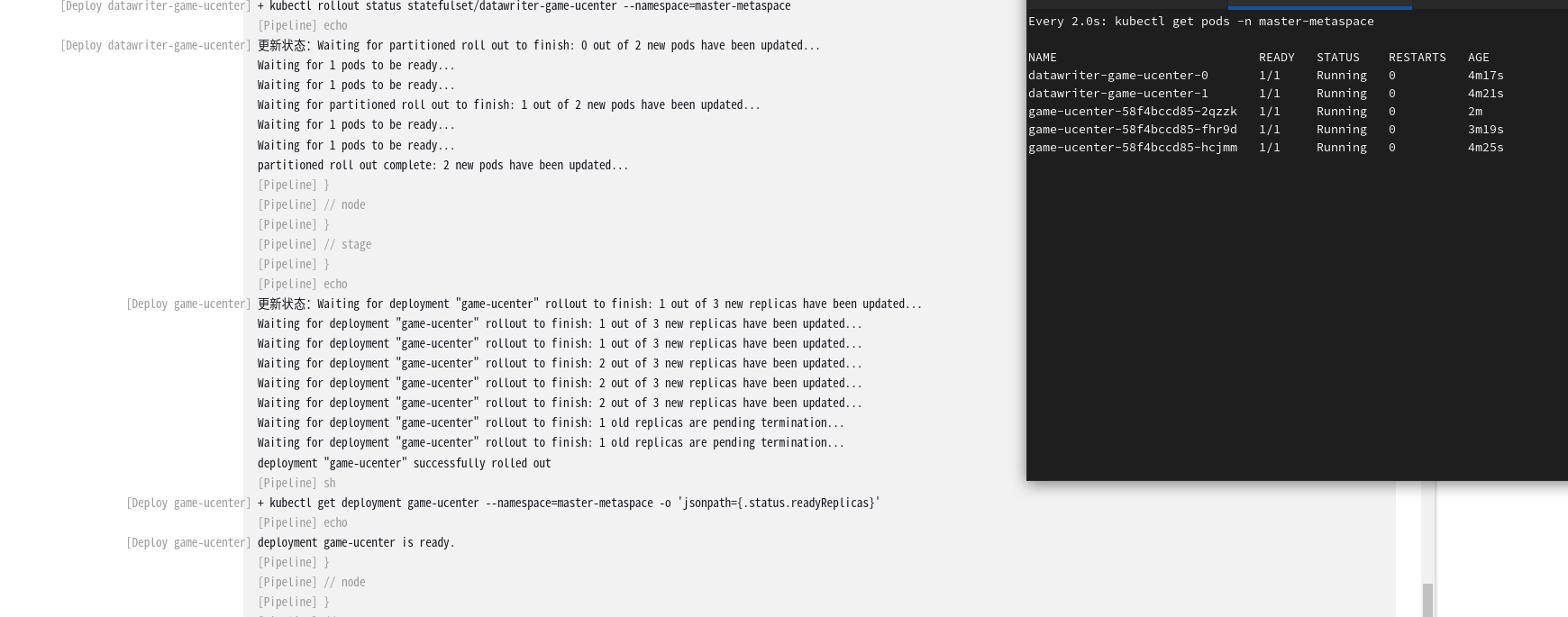
Jenkins Pipeline脚本优化:为Kubernetes应用部署增加状态检测
引言 在软件部署的世界中,Jenkins已经成为自动化流程的代名词。不断变化的技术环境要求我们持续改进部署流程以满足现代应用部署的需要。在本篇博客中,作为一位资深运维工程师,我将分享如何将Jenkins Pipeline进化至不仅能支持部署应用直至R…...
R语言基础 | 安徽某高校《统计建模与R软件》期末复习
第一节 数字、字符与向量 1.1 向量的赋值 c<-(1,2,3,4,5) 1.2 向量的运算 对于向量,我们可以直接对其作加(),减(-),乘(*),除(/)…...

深度神经网络下的风格迁移模型(C#)
版权声明:本文为博主原创文章,转载请在显著位置标明本文出处以及作者网名,未经作者允许不得用于商业目的。 这个是C#版本的,这里就只放出代码。VB.Net版本请参看 深度神经网络下的风格迁移模型-CSDN博客 斯坦福大学李飞飞团队的…...
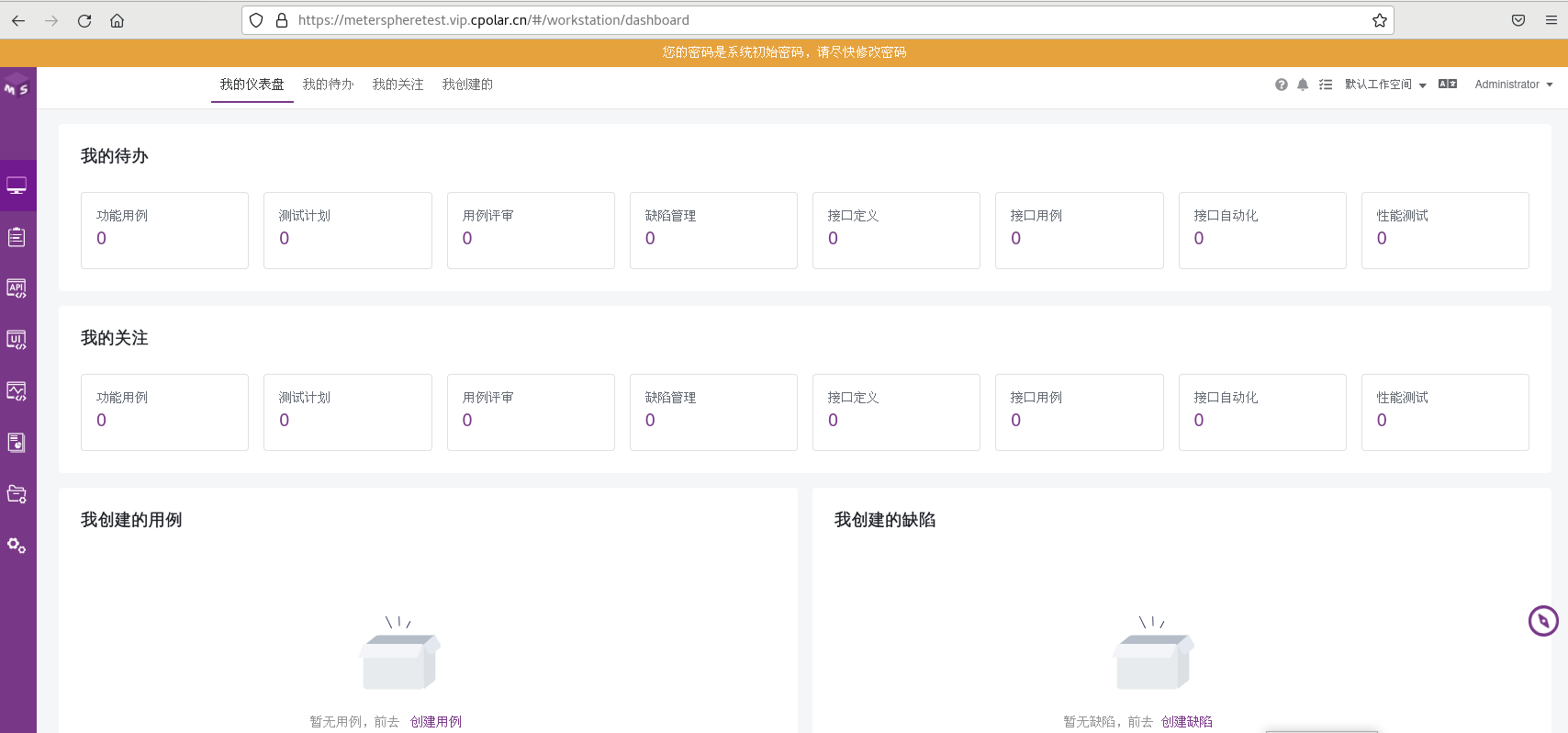
Linux部署MeterSphere结合内网穿透实现远程访问服务管理界面
文章目录 前言1. 安装MeterSphere2. 本地访问MeterSphere3. 安装 cpolar内网穿透软件4. 配置MeterSphere公网访问地址5. 公网远程访问MeterSphere6. 固定MeterSphere公网地址 前言 MeterSphere 是一站式开源持续测试平台, 涵盖测试跟踪、接口测试、UI 测试和性能测试等功能&am…...

MyBatis见解4
10.MyBatis的动态SQL 10.5.trim标签 trim标签可以代替where标签、set标签 mapper //修改public void updateByUser2(User user);<update id"updateByUser2" parameterType"User">update user<!-- 增加SET前缀,忽略,后缀…...
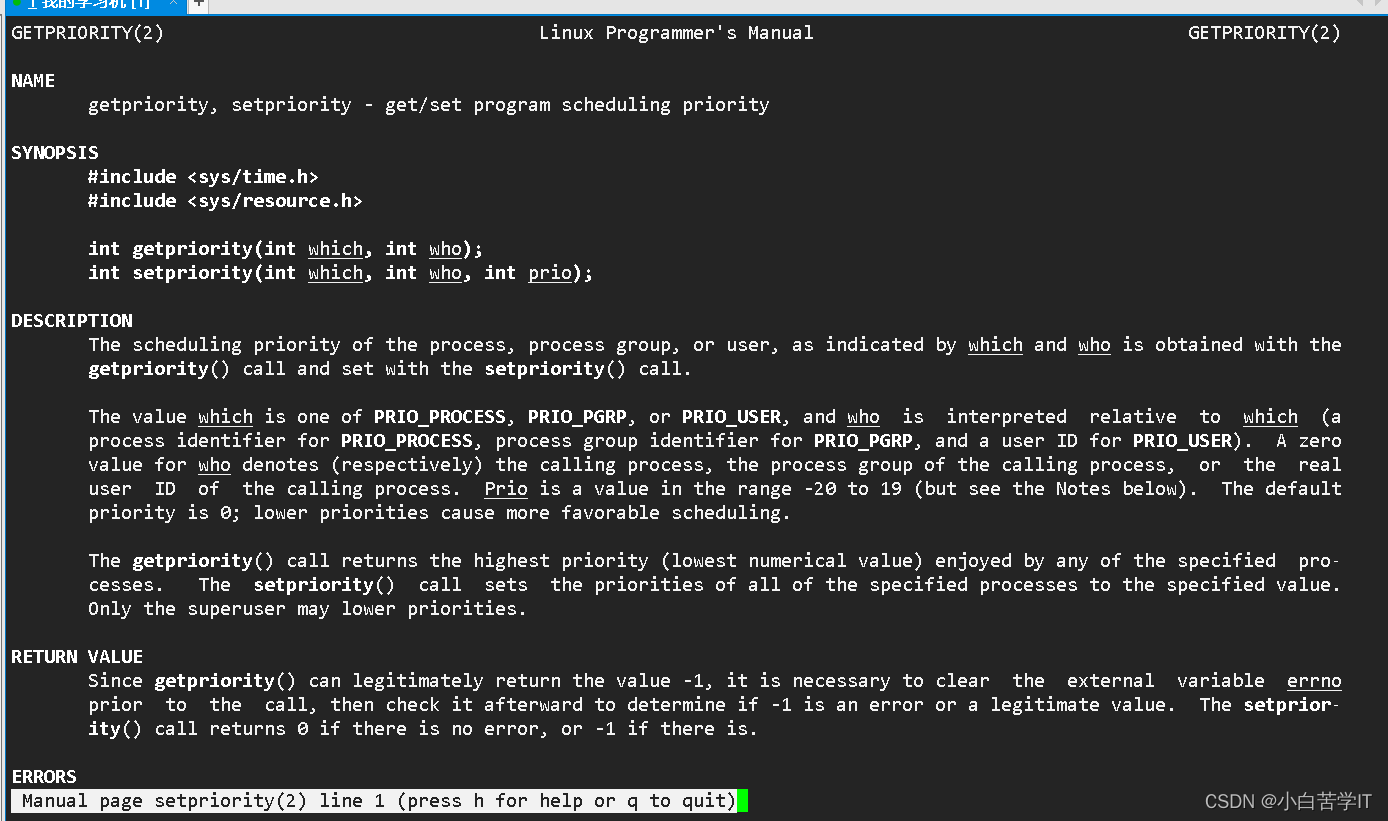
Linux操作系统——进程(三) 进程优先级
进程优先级 首先呢,我们知道一个进程呢(或者也可以叫做一个任务),它呢有时候要在CPU的运行队列中排队,要么有时候阻塞的时候呢又要在设备的等待队列中排队,其实我们排队的本质就是:确认优先级。…...

插入排序详解(C语言)
前言 插入排序是一种简单直观的排序算法,在小规模数据排序或部分有序的情况下插入排序的表现十分良好,今天我将带大家学习插入排序的使用。let’s go ! ! ! 插入排序 插入排序的基本思想是将待排序的序列分为已排序和未排序两部分。初始时,…...
Json和Xml
一、前言 学习心得:C# 入门经典第8版书中的第21章《Json和Xml》 二、Xml的介绍 Xml的含义: 可标记性语言,它将数据以一种特别简单文本格式储存。让所有人和几乎所有的计算机都能理解。 XML文件示例: <?xml version"1.…...
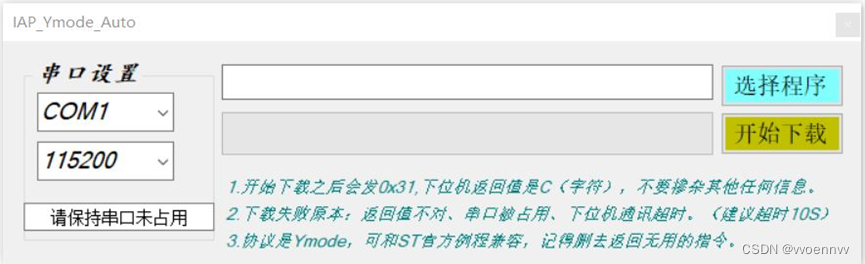
STM32 支持IAP的bootloader开发,使用串口通过Ymodem协议传输固件
资料下载: https://download.csdn.net/download/vvoennvv/88658447 一、概述 关于IAP的原理和Ymodem协议,本文不做任何论述,本文只论述bootloader如何使用串口通过Ymodem协议接收升级程序并进行IAP升级,以及bootloader和主程序两个工程的配置…...

【SVN】centos7搭建svn--亲测能通
centos7.6搭建svn 1 知识小课堂1.1 CentOS1.2 SVN 2 搭建过程2.1 前期准备2.2 通过yum命令安装svnserve2.3 创建版本库目录2.4 创建svn版本库2.5 配置修改2.5 防火墙配置2.6 启动或关闭svn服务器2.6.1 进程守护2.6.2 检测svn端口3690是否已经监听:2.6.3 关闭SVN 2.7…...

MY FILE SERVER: 1
下载地址 https://download.vulnhub.com/myfileserver/My_file_server_1.ova 首先我们需要发现ip 我的kali是59.162所以167就是靶机的 然后我们拿nmap扫一下端口 nmap -sV -p- 192.168.59.167 扫完发现有七个端口开放 按照习惯先看80 没看到有啥有用信息,用nikto扫一下 nik…...
Day70力扣打卡
打卡记录 收集足够苹果的最小花园周长(找规律 二分) 链接 class Solution:def minimumPerimeter(self, neededApples: int) -> int:l, r 1, 10 ** 5while l < r:mid (l r) >> 1if 2 * (2 * (mid ** 3) 3 * (mid ** 2) mid) > nee…...
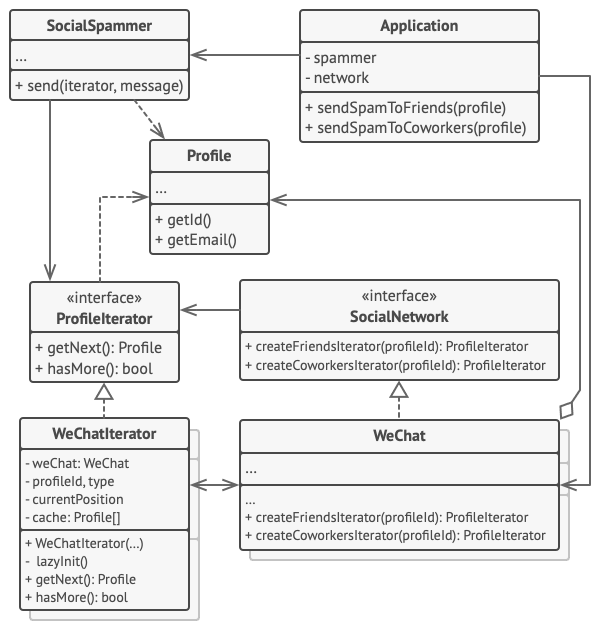
3. 行为模式 - 迭代器模式
亦称: Iterator 意图 迭代器模式是一种行为设计模式, 让你能在不暴露集合底层表现形式 (列表、 栈和树等) 的情况下遍历集合中所有的元素。 问题 集合是编程中最常使用的数据类型之一。 尽管如此, 集合只是一组对象的…...

rsync文件同步
场景:主要是用来发布文件。 一、rsync服务器端架设 1、安装 wget https://download.samba.org/pub/rsync/src/rsync-3.0.6.tar.gz tar -zxvf rsync-3.0.6.tar.gz ./configure --prefix/usr/local/rsync make make install 2、配置 2.1、配置rsyncd.conf 不存在…...

docker 安装mysql 8.0.35
1.拉取镜像 docker pull mysql:8.0.35 2.创建相关挂载目录与文件 mkdir -p /opt/mysql8/conf mkdir -p /opt/mysql8/data mkdir -p /opt/mysql8/logs 或者:mkdir -p /opt/mysql8/{data,conf,logs,mysqld,mysql-files} 文件与文件夹授权:chmod -R 775 /opt/mysql8/* 3.运…...

力扣labuladong一刷day46天并查集
力扣labuladong一刷day46天并查集 文章目录 力扣labuladong一刷day46天并查集一、323. 无向图中连通分量的数目二、130. 被围绕的区域三、990. 等式方程的可满足性 一、323. 无向图中连通分量的数目 题目链接:https://leetcode.cn/problems/number-of-connected-co…...
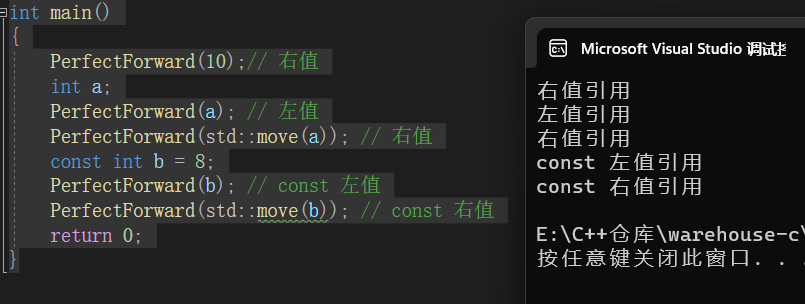
C++11(上):新特性讲解
C11新特性讲解 前言1.列表初始化1.1{ }初始化1.2std::initializer_list 2.类型推导2.1 auto2.2 typeid2.3 decltype 3.范围for4.STL的变化4.1新容器4.2容器的新方法 5.右值引用和移动语义5.1 左值引用和右值引用5.2 左值引用与右值引用比较5.3 右值引用的使用场景5.4 右值、左值…...
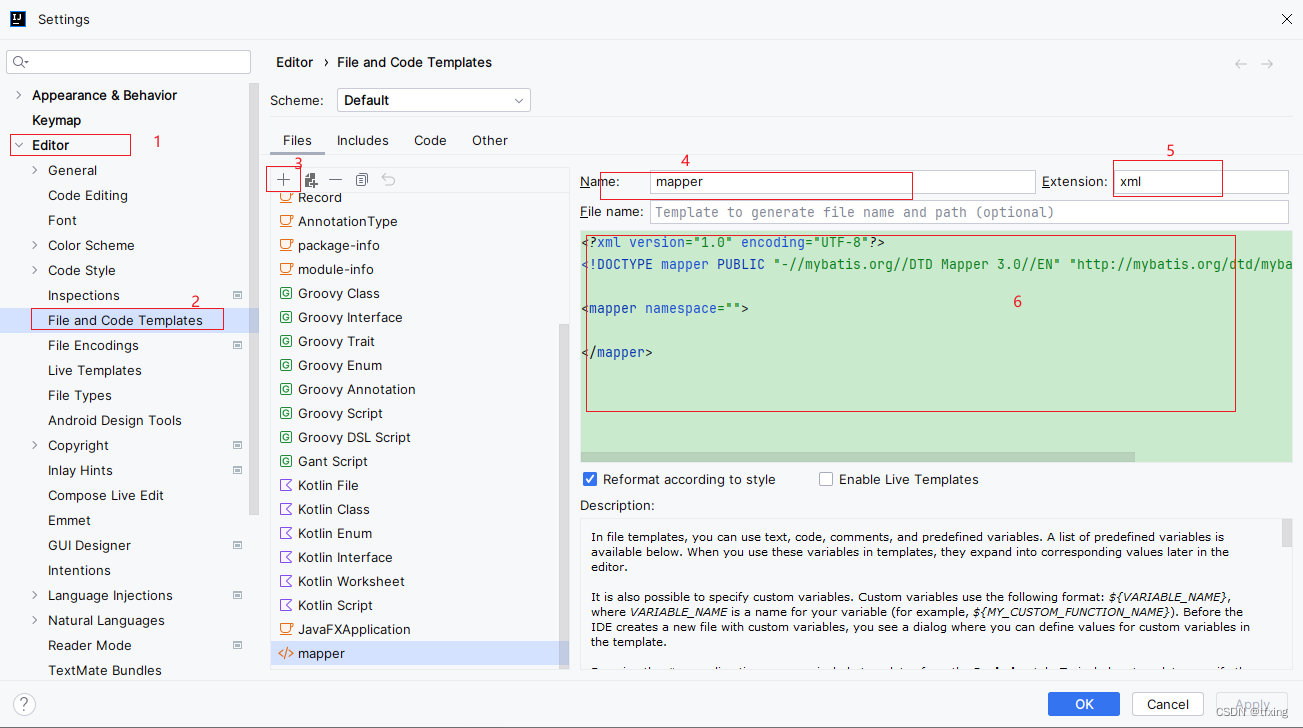
将mapper.xml保存为idea的文件模板
将mapper.xml保存为idea的文件模板 在idea的File and Code Templates中将需要使用模板的内容添加为模板文件。 那么接下来请看图,跟着步骤操作吧。 mapper.xml文件内容 <?xml version"1.0" encoding"UTF-8"?> <!DOCTYPE mapper P…...

使用docker在3台服务器上搭建基于redis 6.x的一主两从三台均是哨兵模式
一、环境及版本说明 如果服务器已经安装了docker,则忽略此步骤,如果没有安装,则可以按照一下方式安装: 1. 在线安装(有互联网环境): 请看我这篇文章 传送阵>> 点我查看 2. 离线安装(内网环境):请看我这篇文章 传送阵>> 点我查看 说明:假设每台服务器已…...

网络六边形受到攻击
大家读完觉得有帮助记得关注和点赞!!! 抽象 现代智能交通系统 (ITS) 的一个关键要求是能够以安全、可靠和匿名的方式从互联车辆和移动设备收集地理参考数据。Nexagon 协议建立在 IETF 定位器/ID 分离协议 (…...

蓝桥杯 2024 15届国赛 A组 儿童节快乐
P10576 [蓝桥杯 2024 国 A] 儿童节快乐 题目描述 五彩斑斓的气球在蓝天下悠然飘荡,轻快的音乐在耳边持续回荡,小朋友们手牵着手一同畅快欢笑。在这样一片安乐祥和的氛围下,六一来了。 今天是六一儿童节,小蓝老师为了让大家在节…...

在 Nginx Stream 层“改写”MQTT ngx_stream_mqtt_filter_module
1、为什么要修改 CONNECT 报文? 多租户隔离:自动为接入设备追加租户前缀,后端按 ClientID 拆分队列。零代码鉴权:将入站用户名替换为 OAuth Access-Token,后端 Broker 统一校验。灰度发布:根据 IP/地理位写…...

Java-41 深入浅出 Spring - 声明式事务的支持 事务配置 XML模式 XML+注解模式
点一下关注吧!!!非常感谢!!持续更新!!! 🚀 AI篇持续更新中!(长期更新) 目前2025年06月05日更新到: AI炼丹日志-28 - Aud…...

Java 二维码
Java 二维码 **技术:**谷歌 ZXing 实现 首先添加依赖 <!-- 二维码依赖 --><dependency><groupId>com.google.zxing</groupId><artifactId>core</artifactId><version>3.5.1</version></dependency><de…...

深入理解Optional:处理空指针异常
1. 使用Optional处理可能为空的集合 在Java开发中,集合判空是一个常见但容易出错的场景。传统方式虽然可行,但存在一些潜在问题: // 传统判空方式 if (!CollectionUtils.isEmpty(userInfoList)) {for (UserInfo userInfo : userInfoList) {…...

系统掌握PyTorch:图解张量、Autograd、DataLoader、nn.Module与实战模型
本文较长,建议点赞收藏,以免遗失。更多AI大模型应用开发学习视频及资料,尽在聚客AI学院。 本文通过代码驱动的方式,系统讲解PyTorch核心概念和实战技巧,涵盖张量操作、自动微分、数据加载、模型构建和训练全流程&#…...

十九、【用户管理与权限 - 篇一】后端基础:用户列表与角色模型的初步构建
【用户管理与权限 - 篇一】后端基础:用户列表与角色模型的初步构建 前言准备工作第一部分:回顾 Django 内置的 `User` 模型第二部分:设计并创建 `Role` 和 `UserProfile` 模型第三部分:创建 Serializers第四部分:创建 ViewSets第五部分:注册 API 路由第六部分:后端初步测…...

深度剖析 DeepSeek 开源模型部署与应用:策略、权衡与未来走向
在人工智能技术呈指数级发展的当下,大模型已然成为推动各行业变革的核心驱动力。DeepSeek 开源模型以其卓越的性能和灵活的开源特性,吸引了众多企业与开发者的目光。如何高效且合理地部署与运用 DeepSeek 模型,成为释放其巨大潜力的关键所在&…...
