【线性代数】决定张成空间的最少向量线性无关吗?
答1:
是的,张成空间的最少向量是线性无关的。
在数学中,张成空间(span space)是一个向量空间,它由一组向量通过线性组合(即每个向量乘以一个标量)生成。如果这组向量是线性无关的(即它们不能被其他向量线性组合得到),那么它们就构成了张成空间的一组基,也就是说,它们生成了整个向量空间。
因此,决定张成空间的最少向量是线性无关的。
 答2:
答2:
是的,决定张成空间的最少向量是线性无关的。
在数学中,如果一组向量能够张成整个空间,那么这组向量就是线性无关的。换句话说,如果存在一组不全为零的标量 使得
,那么这组向量就是线性相关的。
因此,决定张成空间的最少向量是线性无关的。
答3:
是的,决定张成空间的最少向量组称为该空间的一组基。一组基具有两个关键属性:
1. 线性无关:基中的任何向量都不能表示为其他向量的线性组合。
2. 张成空间:基中的向量可以线性组合以任何方式产生该空间中的所有其他向量。
因此,如果你有一个由最少量的向量张成的空间,这些向量必须是线性无关的,否则,如果存在线性相关的向量,那么至少有一个向量是多余的(可以被其他向量线性表示),这意味着你并没有使用最少量的向量,因此组成的不是基。
所以,决定张成空间的最少向量必然构成一组线性无关的向量,即该空间的一组基。
相关文章:

【线性代数】决定张成空间的最少向量线性无关吗?
答1: 是的,张成空间的最少向量是线性无关的。 在数学中,张成空间(span space)是一个向量空间,它由一组向量通过线性组合(即每个向量乘以一个标量)生成。如果这组向量是线性无关的&…...
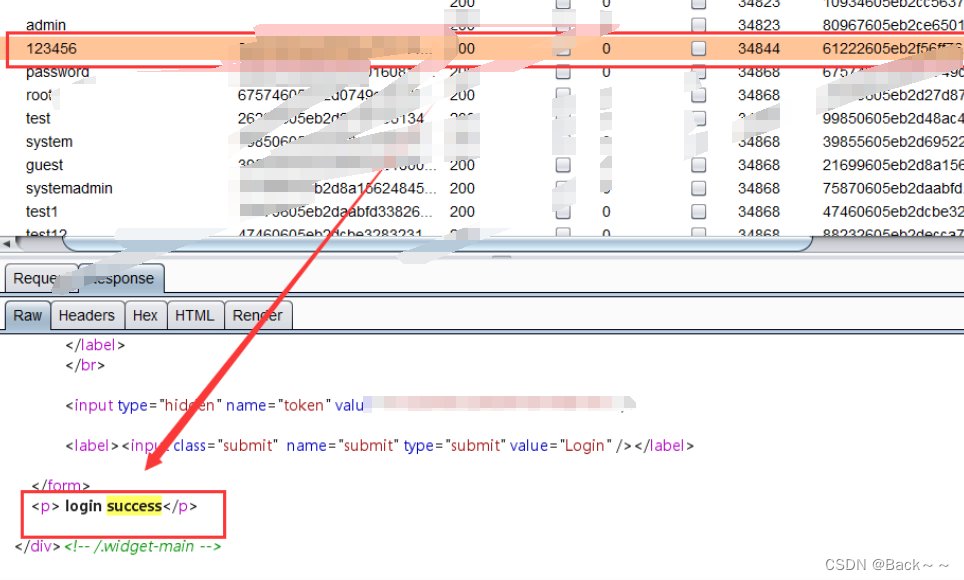
暴力破解(Pikachu)
基于表单的暴力破解 先随便输入一下,然后抓包,进行字典爆破 验证码绕过(on server) server服务端要输入正确的验证码后进行爆破 之后的操作没什么不一样 验证码绕过(on client) 这个也需要输入验证码,但是后面进行字典爆破的时候…...

如何使用CMake查看opencv封装好的函数
当我们有时想查看opencv自带的函数的源代码,比如函数cvCreateImage, 此时我们选中cvCreateImage, 点击鼠标右键->转到定义,我们会很惊讶的发现为什么只看到了cvCreateImage的一个简单声明,而没有源代码呢?这是因为openCV将很多…...

微盛·企微管家:用户运营API集成,电商无代码解决方案
连接电商平台的新纪元:微盛企微管家 随着电子商务的蓬勃发展,电商平台的高效运营已经成为企业成功的关键。在这个新纪元里,微盛企微管家以其创新的无代码开发连接方案,成为企业之间连接电商平台的强大工具。它允许企业轻松集成电…...
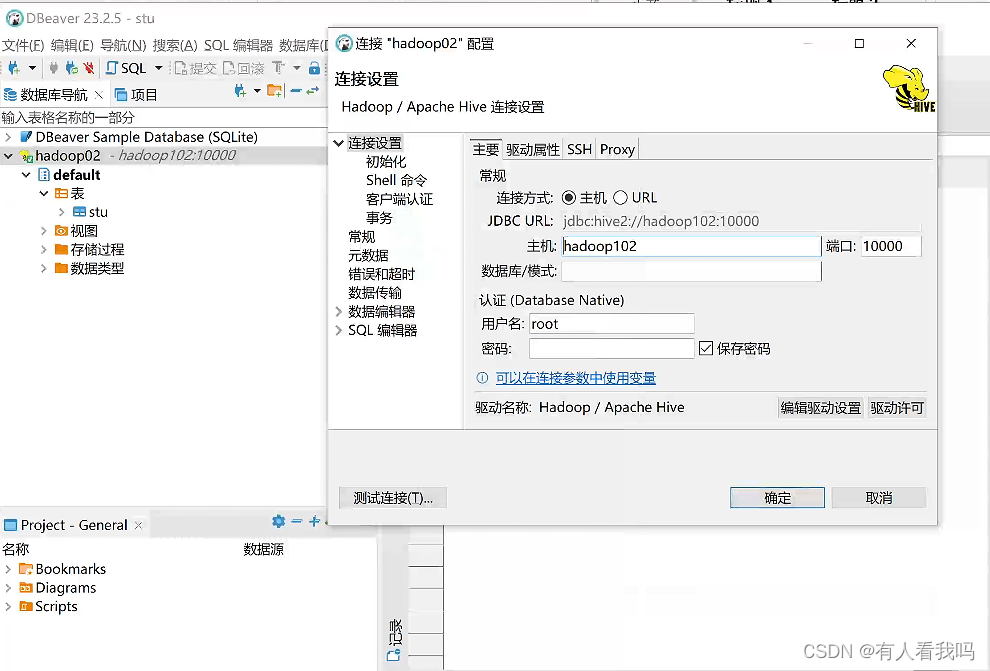
Hive 部署
一、介绍 Apache Hive是一个分布式、容错的数据仓库系统,支持大规模的分析。Hive Metastore(HMS)提供了一个中央元数据存储库,可以轻松地进行分析,以做出明智的数据驱动决策,因此它是许多数据湖架构的关键组…...

CopyOnWriteArrayList源码阅读
1、构造方法 无参构造函数 //创建一个空数组,赋值给array引用 public CopyOnWriteArrayList() {setArray(new Object[0]); }//仅通过getArray / setArray访问的数组。 private transient volatile Object[] array;//设置数组 final void setArray(Object[] a) {arra…...
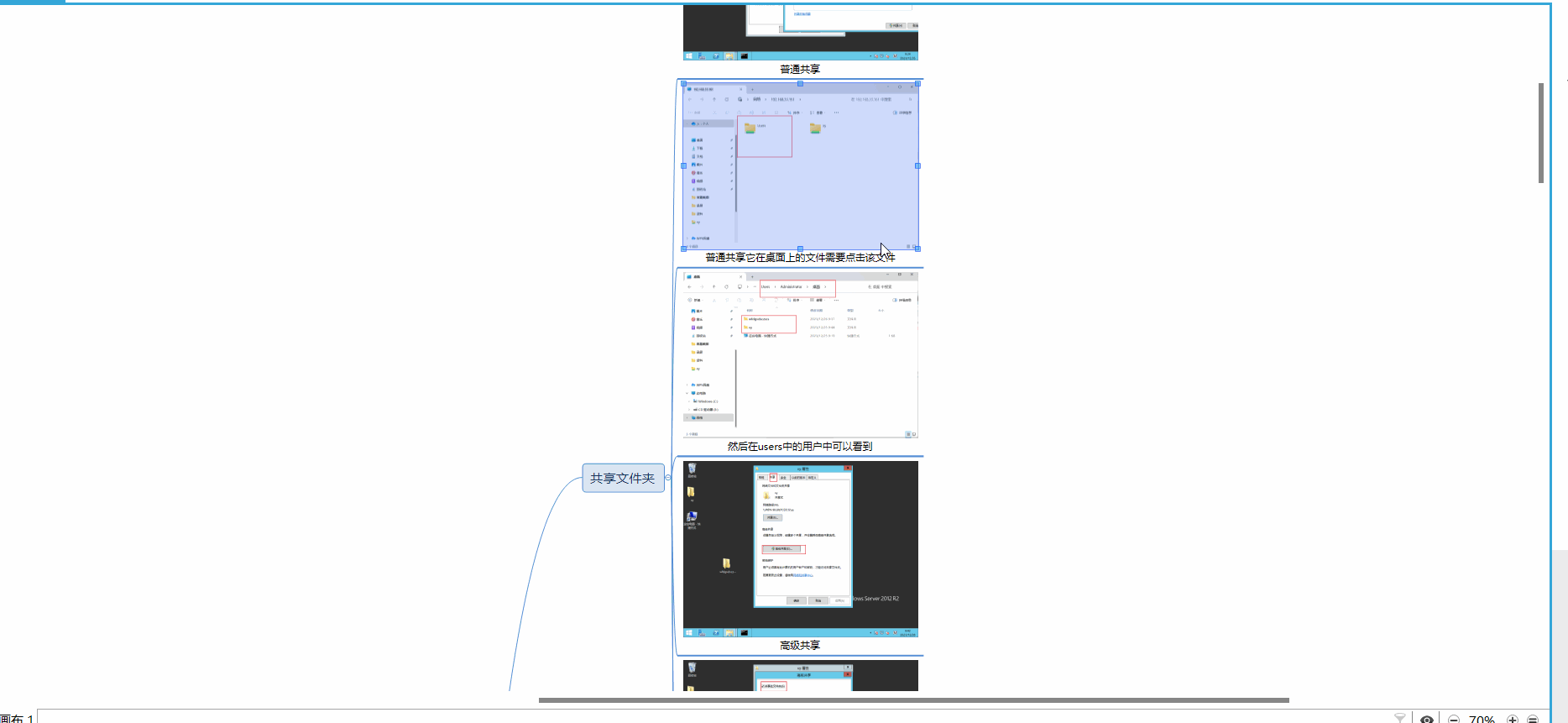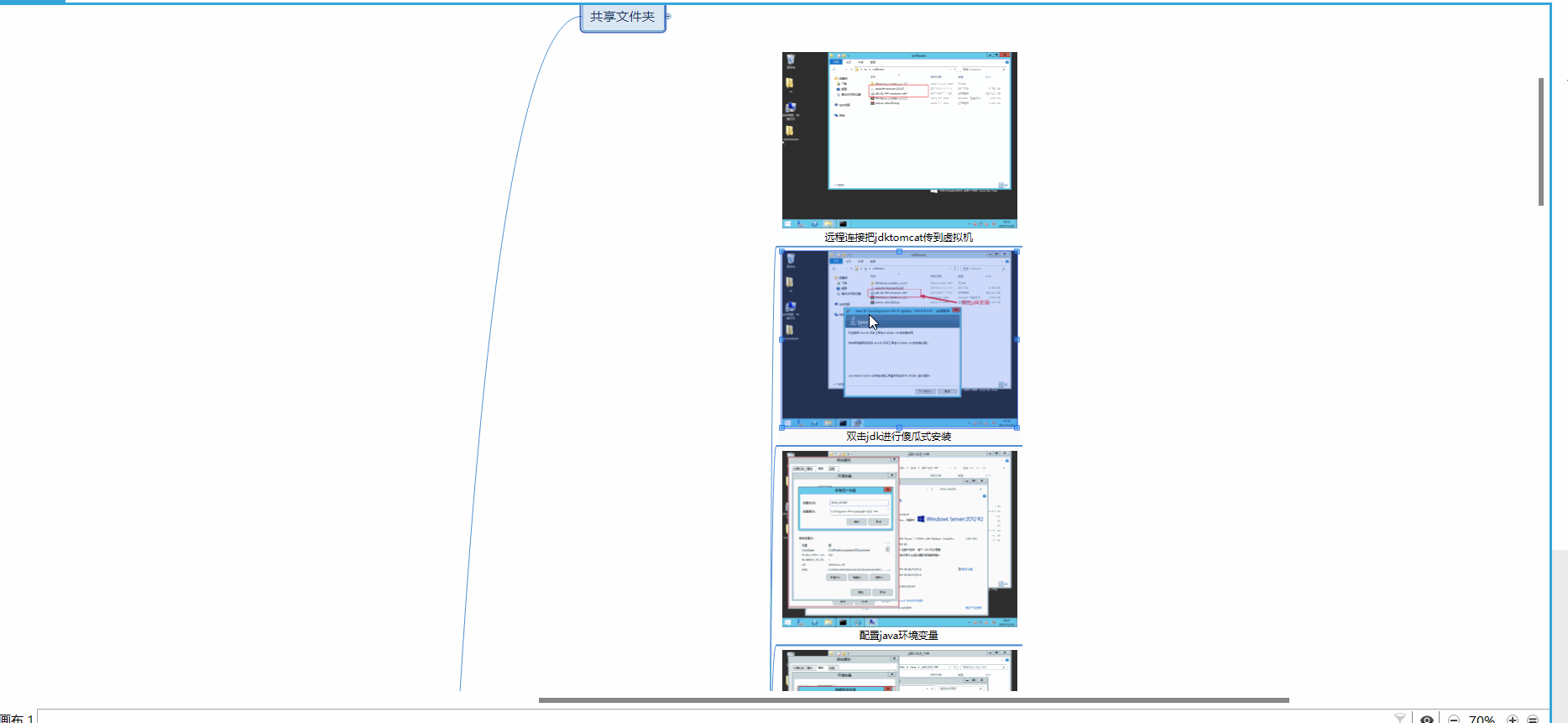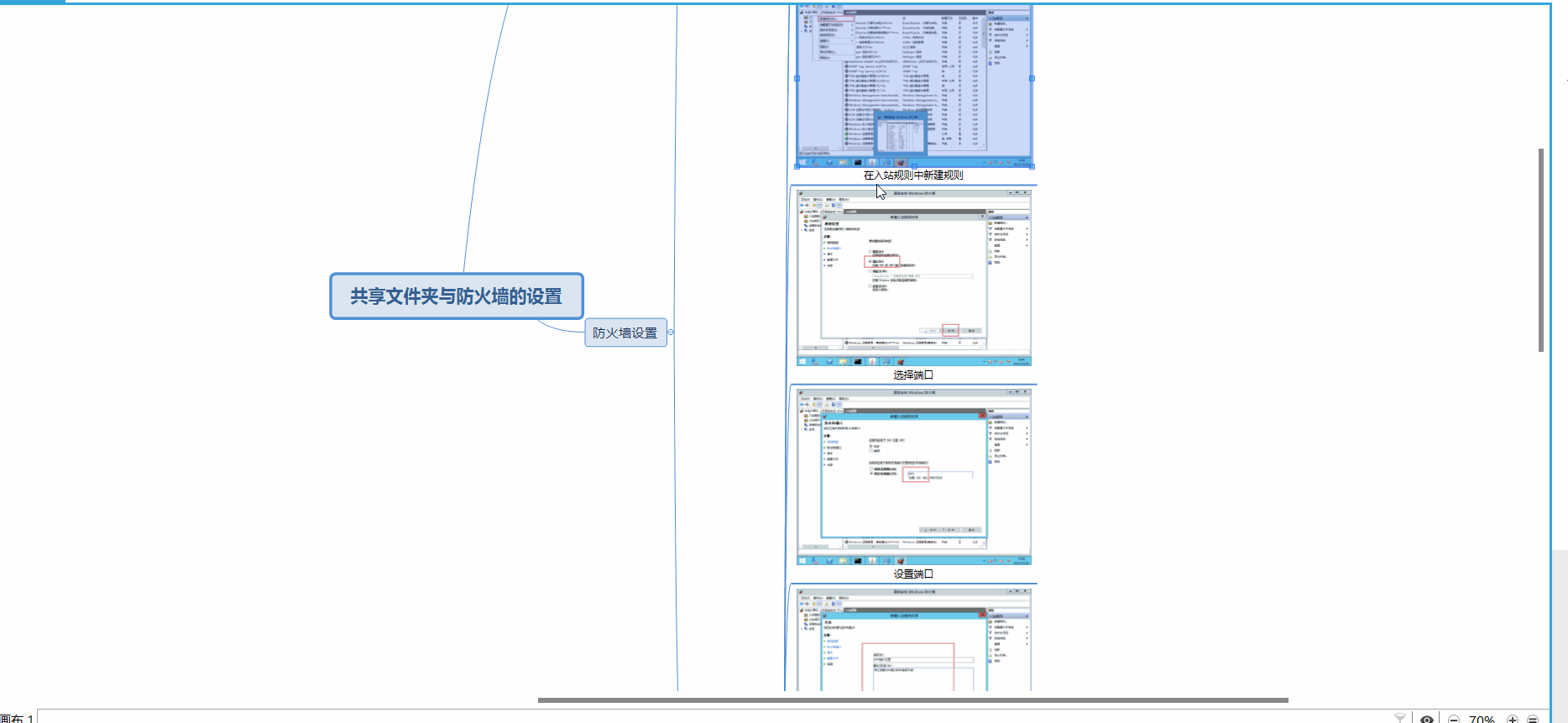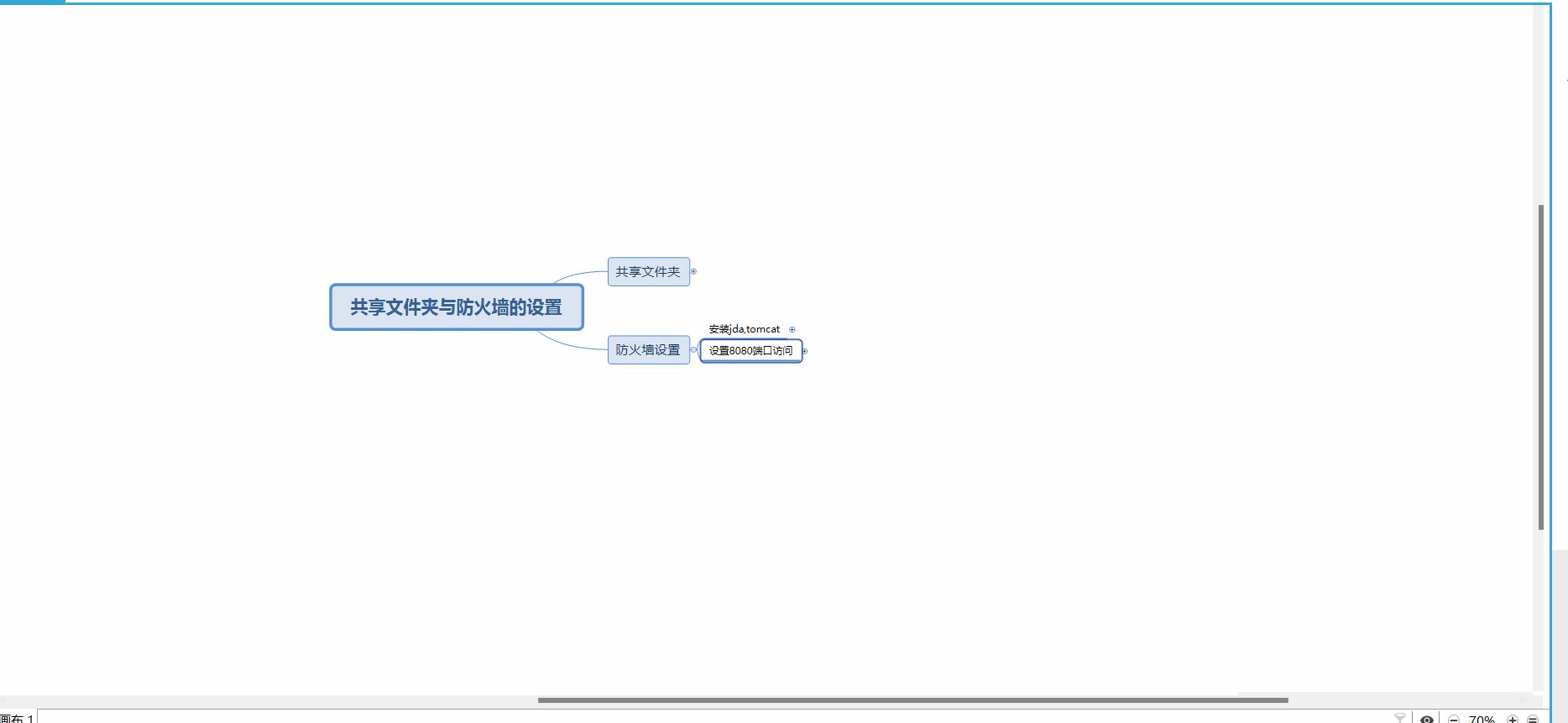
Windows操作系统:共享文件夹,防火墙的设置
1.共享文件夹 1.1 共享文件夹的优点 1.2 共享文件夹的优缺点 1.3 实例操作 编辑 2.防火墙设置 2.1 8080端口设置 3.思维导图 1.共享文件夹 1.1 共享文件夹的优点 优点 协作和团队合作:共享文件夹使多个用户能够在同一文件夹中协作和编辑文件。这促进了团…...
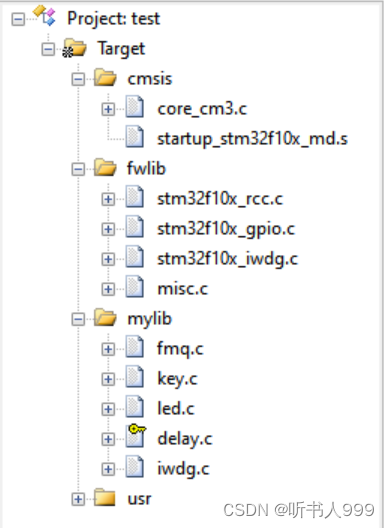
STM32独立看门狗
时钟频率 40KHZ 看门狗简介 STM32F10xxx 内置两个看门狗,提供了更高的安全性、时间的精确性和使用的灵活性。两个看 门狗设备 ( 独立看门狗和窗口看门狗 ) 可用来检测和解决由软件错误引起的故障;当计数器达到给 定的超时值时,触发一个中…...

财务数据智能化:用AI工具高效制作财务分析PPT报告
Step1: 文章内容提取 WPS AI 直接打开文件,在AI对话框里输入下面指令: 假设你是财务总监,公司考虑与茅台进行业务合作、投资或收购,请整合下面茅台2021年和2022年的财务报告信息。整理有关茅台财务状况和潜在投资回报的信息&…...

vue3中使用three.js记录
记录一下three.js配合vitevue3的使用。 安装three.js 使用npm安装: npm install --save three开始使用 1.定义一个div <template><div ref"threeContainer" class"w-full h-full"></div> </template>可以给这个di…...
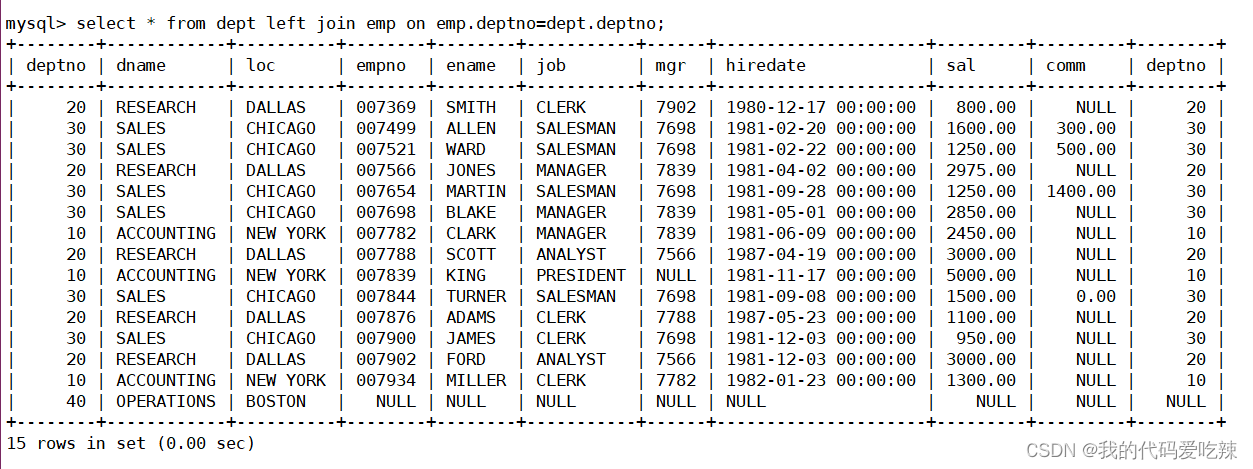
MySQL——表的内外连接
目录 一.内连接 二.外连接 1.左外连接 2.右外连接 一.内连接 表的连接分为内连和外连 内连接实际上就是利用where子句对两种表形成的笛卡儿积进行筛选,我们前面学习的查询都是内连接,也是在开发过程中使用的最多的连接查询。 语法: s…...

基于IPP-FFT的线性调频Z(Chirp-Z,CZT)的C++类库封装并导出为dll(固定接口支持更新)
上一篇分析了三种不同导出C++类方法的优缺点,同时也讲了如何基于IPP库将FFT函数封装为C++类库,并导出为支持更新的dll库供他人调用。 在此基础上,结合前面的CZT的原理及代码实现,可以很容易将CZT变换也封装为C++类库并导出为dll,关于CZT的原理和实现,如有问题请参考: …...

【C语言】指针
基本概念 在C语言中,指针是一种非常重要的数据类型,它用于存储变量的内存地址。指针提供了对内存中数据的直接访问,使得在C语言中可以进行灵活的内存操作和数据传递。以下是关于C语言指针的一些基本概念: 1. 指针的声明ÿ…...

PostgreSql 索引使用技巧
索引种类详情可参考《PostgreSql 索引》 一、适合创建索引的场景 经常与其他表进行连接的表,在连接字段上应该建索引。经常出现在 WHERE 子句中的字段,特别是大表的字段,应该建索引。经常出现在 ORDER BY 子句中的字段,应该建索…...

【华为数据之道学习笔记】6-7打造业务自助分析的关键能力
华为公司将自助分析作为一种公共能力,在企业层面进行了统一构建。一方面,面向不同的消费用户提供了差异性的能力和工具支撑;另一方面,引入了“租户”概念,不同类型的用户可以在一定范围内分析数据、共享数据结果。 1. …...

K8S从harbor中拉取镜像的规则imagePullPolicy
1、参数 配制参数为:imagePullPolicy: 可以选择的值有:Always,IfNotPresent,Never 2、参数结果 如果pod的镜像拉取策略为imagePullPolicy: Always:当harbor不能运行后,pod会一直从harbor上拉…...
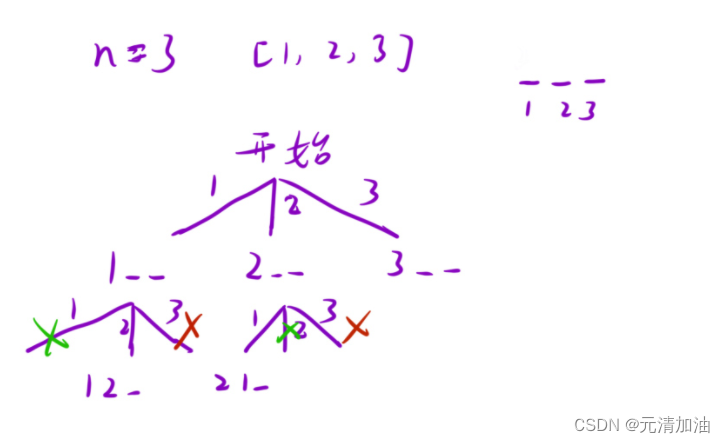
LeetCode刷题--- 优美的排列
个人主页:元清加油_【C】,【C语言】,【数据结构与算法】-CSDN博客元清加油_【C】,【C语言】,【数据结构与算法】-CSDN博客 个人专栏 力扣递归算法题 http://t.csdnimg.cn/yUl2I 【C】 http://t.csdnimg.cn/6AbpV 数据结构与算法 http://t.cs…...
关于edge浏览器以及插件推荐【亲测好用】
一.edge浏览器介绍 Edge 浏览器是由微软公司开发的一款新一代网络浏览器。它最初于2015年发布,是微软Windows 10 操作系统的默认浏览器,后来还推出了适用于 Android 和 iOS 等移动设备的版本。Edge 浏览器采用了全新的浏览器内核,称为 Micros…...
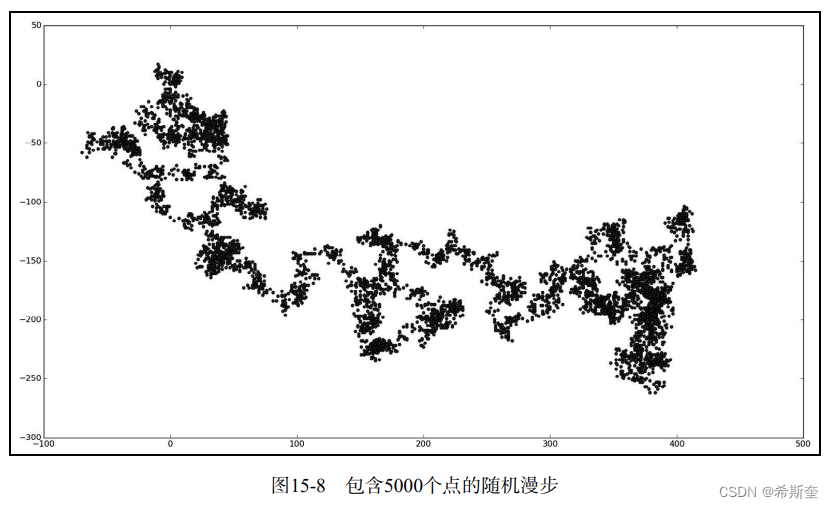
关于“Python”的核心知识点整理大全43
目录 编辑 15.2.3 使2散点图并设置其样式 scatter_squares.py 15.2.4 使用 scatter()绘制一系列点 scatter_squares.py 15.2.5 自动计算数据 scatter_squares.py 15.2.6 删除数据点的轮廓 15.2.7 自定义颜色 15.2.8 使用颜色映射 scatter_squares.py 注意 15.2.9…...

Android Framework一些问题思考
一,zygote通信为什么用socket,而不是binder? 1,binder通信依赖用户空间进程Servicemanager,socket通信不依赖用户空间进程。zygote与servicemanager, surfaceflinger等都是通过各自init.rc文件被init进程解析加载,时…...

国防科技大学计算机基础课程笔记02信息编码
1.机内码和国标码 国标码就是我们非常熟悉的这个GB2312,但是因为都是16进制,因此这个了16进制的数据既可以翻译成为这个机器码,也可以翻译成为这个国标码,所以这个时候很容易会出现这个歧义的情况; 因此,我们的这个国…...

conda相比python好处
Conda 作为 Python 的环境和包管理工具,相比原生 Python 生态(如 pip 虚拟环境)有许多独特优势,尤其在多项目管理、依赖处理和跨平台兼容性等方面表现更优。以下是 Conda 的核心好处: 一、一站式环境管理:…...

RocketMQ延迟消息机制
两种延迟消息 RocketMQ中提供了两种延迟消息机制 指定固定的延迟级别 通过在Message中设定一个MessageDelayLevel参数,对应18个预设的延迟级别指定时间点的延迟级别 通过在Message中设定一个DeliverTimeMS指定一个Long类型表示的具体时间点。到了时间点后…...
)
云计算——弹性云计算器(ECS)
弹性云服务器:ECS 概述 云计算重构了ICT系统,云计算平台厂商推出使得厂家能够主要关注应用管理而非平台管理的云平台,包含如下主要概念。 ECS(Elastic Cloud Server):即弹性云服务器,是云计算…...

从WWDC看苹果产品发展的规律
WWDC 是苹果公司一年一度面向全球开发者的盛会,其主题演讲展现了苹果在产品设计、技术路线、用户体验和生态系统构建上的核心理念与演进脉络。我们借助 ChatGPT Deep Research 工具,对过去十年 WWDC 主题演讲内容进行了系统化分析,形成了这份…...

【Linux】C语言执行shell指令
在C语言中执行Shell指令 在C语言中,有几种方法可以执行Shell指令: 1. 使用system()函数 这是最简单的方法,包含在stdlib.h头文件中: #include <stdlib.h>int main() {system("ls -l"); // 执行ls -l命令retu…...

在rocky linux 9.5上在线安装 docker
前面是指南,后面是日志 sudo dnf config-manager --add-repo https://download.docker.com/linux/centos/docker-ce.repo sudo dnf install docker-ce docker-ce-cli containerd.io -y docker version sudo systemctl start docker sudo systemctl status docker …...

2025 后端自学UNIAPP【项目实战:旅游项目】6、我的收藏页面
代码框架视图 1、先添加一个获取收藏景点的列表请求 【在文件my_api.js文件中添加】 // 引入公共的请求封装 import http from ./my_http.js// 登录接口(适配服务端返回 Token) export const login async (code, avatar) > {const res await http…...

数据库分批入库
今天在工作中,遇到一个问题,就是分批查询的时候,由于批次过大导致出现了一些问题,一下是问题描述和解决方案: 示例: // 假设已有数据列表 dataList 和 PreparedStatement pstmt int batchSize 1000; // …...

使用 SymPy 进行向量和矩阵的高级操作
在科学计算和工程领域,向量和矩阵操作是解决问题的核心技能之一。Python 的 SymPy 库提供了强大的符号计算功能,能够高效地处理向量和矩阵的各种操作。本文将深入探讨如何使用 SymPy 进行向量和矩阵的创建、合并以及维度拓展等操作,并通过具体…...
