遗传算法的应用——求解一元函数的极值

1 基本概念

• 遗传算法(Genetic Algorithm,GA)是模拟生物在自然环境中遗传和进化过程从而形成的随机全局搜索和优化方法，它是一种并行的、高效的、具有自适应能力的全局搜索算法，它充分体现了适者生存的生物进化思想，能在搜索过程中自动获取和积累有关搜索空间的知识，并自适应地控制搜索过程以求得最优解。
• 遗传算法能有效求解NP问题和非线性、多峰函数优化及多目标优化问题。
• 遗传算法的三个最重要操作选择(复制) -> 交叉 -> 变异
• 遗传算法：
  • 以决策变量的编码作为运算对象
  • 直接以目标函数值作为搜索信息
  • 同时使用多个搜索点的搜索信息
  • 是一种基于概率的搜索方法
  • 求解最大值问题（最小值问题理论上添一个负号就是最大值问题，还有其他方法可以转换问题的导向）
• 遗传算法在进化搜索中基本不用外部信息，仅以适应度函数为依据
• 但是基本遗传算法的局部搜索能力较差，有“早熟”缺陷，不能保证算法收敛
• 下边对遗传算法中用到的几个重要的参数进行一个简单的说明：
  • 群体规模：群体规模太小时，算法的搜索效果通常较差，容易陷入局部最优；群体规模太大时，算法的计算复杂度将会变大。一般取值为[10,200]；
  • 交叉概率：在基本遗传算法中，将交叉算子作为遗传算法最重要的操作。较大的交叉概率可以增强算法开辟新的搜索区域的能力，但高性能的模式，也就是二进制组合遭到破坏的可能性增大；交叉概率太低可能会导致算法陷入迟钝状态。一般取值为[0.4,0.99]；
  • 变异概率：变异算法的主要目的是保持群体的多样性。低的变异概率可以防止群体中重要基因的丢失；变异概率太大时，算法就变成了纯粹的随机搜索算法。一般取值为[0.0001,0.1]；

2 预备知识

3.1 模拟二进制转化为十进制的方法

      在遗传算法中，通常会涉及到二进制到十进制的转换，所以需要掌握这个方法，那么为什么说是模拟二进制转为十进制的方法呢，因为我们在代码中通常不是真正的一串二进制数字，而是由一个向量，其中存放许多0101这样的数字，如a=[0 1 0 1]，这样就模拟了一个二进制数，那么它对应的十进制就是5，在matlab中有两个方法，这两种方法对于大量的数据其转换速度有较大差异，请合理选择，如果有其他方法，请各位朋友留言。

%% 法一 通过循环实现
a = [1 0 0 1 1 0 0 1];
deca = 0;
for i = 1:length(a)deca = a(i)*2^(i-1) + a;
end%% 法二 通过强制转换实现(调用库函数)
a = [1 0 0 1 1 0 0 1];
deca = bin2dec(char('0'+ a));

3.2 轮盘赌选择算法

       轮盘赌选择算法是遗传算法中，进行复制操作的一种常用算法，在该方法中，各个个体的选择概率和其适应度值成比例，适应度越大，选中概率也越大。但实际在进行轮盘赌选择时个体的选择往往不是依据个体的选择概率，而是根据“累积概率”来进行选择。我将通过一个抽奖的例子进行一个简单地介绍（参考文章：轮盘赌选择算法）：

等级	一等奖	二等奖	三等奖
选择概率	0.2	0.5	0.3
累计概率	0.2	0.7	1.0

可以从概论论的角度出发，先简单地将选择概率理解为概率密度函数，设xi(i=1,2,3)表示获奖等级，则f(xi)表示该等级对应的适应度，则xi被选中的概率Pxi可以被表示为：

将累计概率Qxi理解为概率分布函数，则Qxi可以表示为从xi开始往前的所有的概率的累加和：

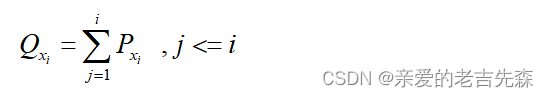
1. 计算个体的被选择概率（概率密度函数）
2. 计算各个部分的累计概率（概率分布函数–离散型）
3. 生成一个[0,1]区间内均匀分布的随机实数，代表此时轮盘的旋转位置（这里就可以理解为什么用累计概率了）
4. 找到累计概率中第一个大于或等于第3步产生的随机数的索引，这个索引就是轮盘赌算法选择的那个个体（不理解可以先看代码）

以一个抽奖问题为导引的轮盘赌算法实例Matlab代码如下：

clc
clear% 定义奖项及其中奖概率
awards = {'一等奖', '二等奖', '三等奖', '四等奖', '五等奖'};
P = [0.1, 0.2, 0.3, 0.2, 0.2]; % 中奖概率
cumP = cumsum(P);    % 累计概率% 模拟抽奖过程
N = 1000; % 模拟次数
results = zeros(1, N); % 存储每次抽奖的结果
for i = 1:N% 生成一个随机数，代表轮盘的旋转位置pos = rand();% 根据轮盘赌算法确定中奖等级level = find(cumP >= pos, 1);% 存储结果results(i) = level;
end% 统计中奖次数
winCounts = histcounts(results, 1:(length(awards) + 1));% 显示结果
disp('中奖统计：');
for i = 1:length(awards)fprintf('%s：%d次\n', awards{i}, winCounts(i));
end

上述代码中，有两行代码需要自己好好理解一下：

% 根据轮盘赌算法确定中奖等级
level = find(cumP >= pos, 1);% 统计中奖次数
winCounts = histcounts(results, 1:(length(awards) + 1));

第一个地方不明白可以自己手动推一下，第二个地方是因为用到了直方图 bin 计数函数，因为results里边全部是存放的等级，用这个函数就可以很快的统计出每个等级在results中出现的次数。
一次统计的结果如下：

3 问题

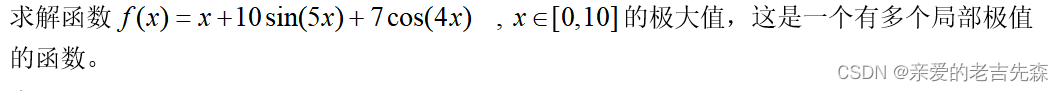
4 Matlab代码

clear
close all
clcT1 = cputime;
%% 初始化参数
NP = 50;    % 种群数量（染色体数目，一个染色体就相当于是一个个体）
L = 20;     % 二进制位串长度
Pc = 0.8;   % 交叉概率
Pm = 0.05;  % 变异概率
G = 100;    % 最大遗传次数
Xs = 10;    % 搜索上限
Xx = 0;     % 搜索下限（这个是随自变量的取值范围确定的，我们已经知道了函数的取值范围）
f = randi([0,1],NP,L);  % 随机获得初始种群（种群里有NP个个体，每个个体的基因位数为L,用0,1模拟二进制）
trace = zeros(1,G); % 历代最优适应度
%% 遗传算法主体
for k = 1:GFit = zeros(1,NP);  % 种群中每个个体的适应度x = zeros(1,NP);    % 存放二进制数对应的十进制数,我把它定义为虚表现型（注意这个并不是真正的解集，还需要做一个映射）%%% 将二进制解码为定义域内的十进制（让二进制和十进制一一对应起来）for i = 1:NPU = f(i,:); % （基因型）U存放的就是一个个体的基因(一串二进制位，这里是用01模拟的)m = 0;      % （伪表现型）这是U对应的十进制% m = bin2dec(char('0'+ U)); 可以用这句话直接实现进制的转换for j = 1:Lm = U(j)*2^(j-1) + m;end% （实表现型）将十进制转换为对应的表现型（x）% 这段代码的实际含义是将通过随机0，1序列转换而来的十进制数，与定义域内的数一一对应起来，% 否则通过随机0，1序列转换而来的十进制数根本没有实际含义，无法和定义域里联系起来% 但是这个定义的法则是通过这个公式确定的，有什么具体其他规范吗？或者其他的定义法则x(i) = Xx + m*(Xs-Xx)/(2^L - 1);   % 将二进制对应的十进制数映射到定义域中（请记住这种映射的方法）Fit(i) = GetFit(x(i));  % 计算这个个体的适应度endmaxFit = max(Fit);  % 找到最大的适应度值minFit = min(Fit);  % 找到最小的适应度值rr = find(Fit == max(Fit));  % 找到最大适应度值对应的个体编号% 最优个体的基因% 因为最大适应度值可能不止一个，可能有多个最大值，因此用rr(1)取第一个最大值对应的个体fBest = f(rr(1),:);   % 最优个体的基因型xBest = x(rr(1));     % 最优个体的实表现型Fit = (Fit-minFit)/(maxFit-minFit); % 将适应度做归一化处理(请记住这种归一化的方法)%%% 基于轮盘赌的复制操作sumFit = sum(Fit);fitValue = Fit./sumFit;         % 求每个个体的适应度值占总的适应度值的百分比fitvalue = cumsum(fitValue);    % 适应度值的累加和ms = sort(rand(NP,1));fiti = 1;   % 记录当前适应度的索引（在轮盘赌选择的过程中，fiti 用于追踪当前适应度的位置）newi = 1;   % 记录新个体的索引（轮盘赌选择的过程中，newi 用于确定新种群中的位置，即确定新个体的存放位置。）while newi <= NPif(ms(newi) < fitvalue(fiti))nf(newi,:) = f(fiti,:);newi = newi + 1;elsefiti = fiti + 1;endend%%% 基于概率的交叉操作(不懂请画图理解)for i = 1:2:NP % i是奇数号染色体if rand < Pcq = randi([0,1],1,L); % 随机生成一个交换flag(为1的位置对应的基因型之间进行交换)for j = 1:Lif q(j) == 1% 交换等位基因temp = nf(i+1,j);nf(i+1,j) = nf(i,j);nf(i,j) = temp;endendendend%%% 基于概率的变异操作i = 1;while i <= round(NP*Pm)h = randi([1,NP],1,1);   % 在种群中随机选一个染色体来变异for j = 1:round(L*Pm)g = randi([1,L],1,1);% 随机选取一个需要变异的基因数nf(h,g) = ~nf(h,g);  % 将染色体nf中第h个个体的第g个基因取反，就是变异了endi = i + 1;endf = nf; f(1,:) = fBest;    % 保留最优个体在新种群中trace(k) = maxFit; % 历代最优适应度
endT2 = cputime;
timeConsume = T2 -T1;
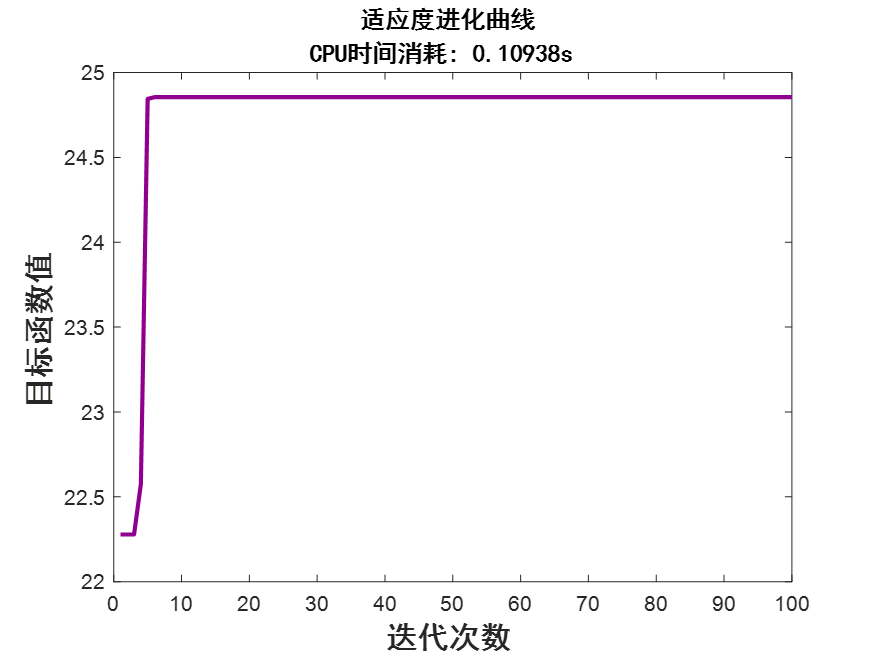
%% 适应度进化曲线
figure(Color=[1 1 1])
plot(trace,LineWidth=2,Color=[0.56 0 0.56]);
xlabel("迭代次数",FontName="黑体",FontWeight="bold",FontSize=15);
ylabel("目标函数值",FontName="黑体",FontWeight="bold",FontSize=15);
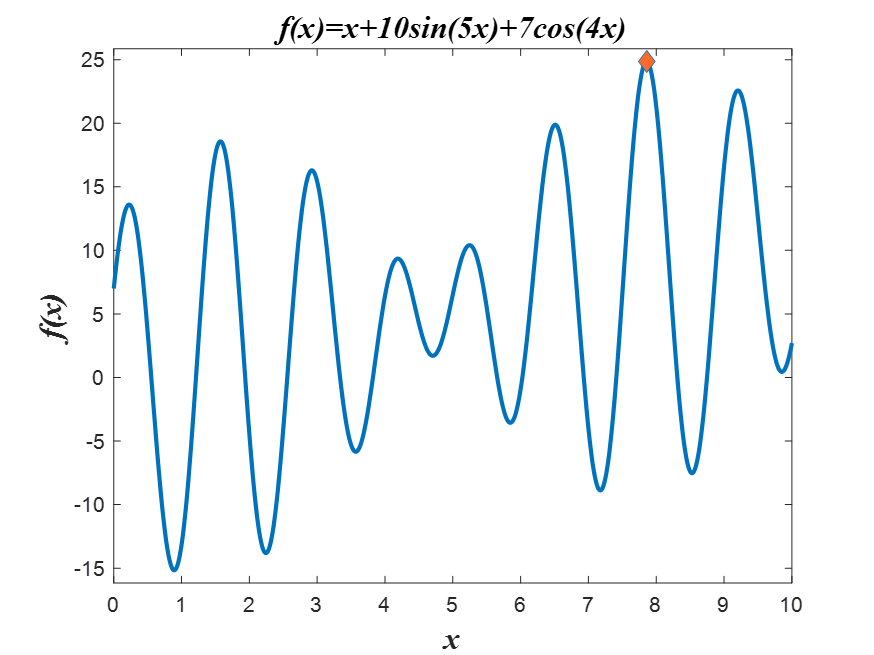
title("适应度进化曲线","CPU时间消耗: "+timeConsume + 's',FontName="黑体",FontWeight="bold",FontSize=12);%% 做出原始图像
x = 0:0.01:10;
y = x + 10*sin(5*x) + 7*cos(4*x);
figure(Color=[1 1 1])
plot(x,y,lineWidth=2);
ylim([min(y)-1,max(y)+1]);
xlabel("x",FontName="Times new Roman"...,FontAngle="italic",FontWeight="bold",FontSize=15);
ylabel("f(x)",FontName="Times new Roman"...,FontAngle="italic",FontWeight="bold",FontSize=15);
title("f(x)=x+10sin(5x)+7cos(4x)",FontName="Times new Roman"...,FontAngle="italic",FontWeight="bold",FontSize=15);
hold on
z = abs(y - max(trace));
x = x(z == min(z));
plot(x(1),max(trace),'r*');%% 适应度函数
function result = GetFit(x)% 这里选择的适应度函数就是目标函数（实际上适应度函数要求为一个非负的函数）result = x + 10*sin(5*x) + 7*cos(4*x);
end

5 运行效果

6 总结

之前本科的时候也做过一些关于遗传算法的实际应用，但是很多是复用别人的代码，简单地修修改改，不过后边很长时间都没有再用了，导致很多知识已经忘记了，所以写算法还是要常加联系。上述代码可能还有许多错误和很多值得优化的地方，恳请各位老师留言，批评指教。