线性代数基础【3】向量
第一节 向量的概念与运算
一、基本概念
①向量

②向量的模(长度)

③向量的单位化

④向量的三则运算
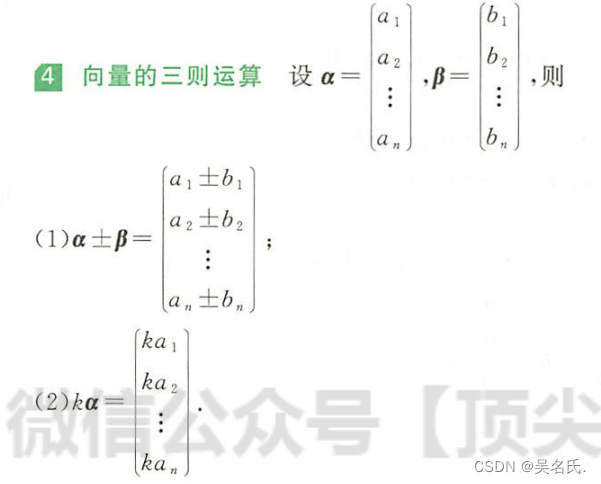
⑤向量的内积

二、向量运算的性质
(一)向量三则运算的性质
- α + β = β + α
- α + (β + γ) = (α + β) + γ
- k (α + β) = kα + kβ
- (k + l) α = kα + lα
(二)向量内积运算的性质
- (α , β) = (β , α) = α^Tβ = β^Tα
- (α , α) = α^Ta = |α|^2 , 且(a,a)-0的充分必要条件是a=0
- (α , k1β1 + k2β2 + … + knβn) = k1(α1 , β1) + k2(α2 , β2) +… + kn(αn , βn)
- 若(α , β) = 0 ←→ a1b1 + a2b2 + … + anbn = 0, 称a,β正交,记为a⊥β,特别地,零向量与任何向量正交
第二节 向量组的相关性与线性表示
一、向量的相关性与线性表示理论的背景
对齐次线性方程组

及非齐次线性方程组
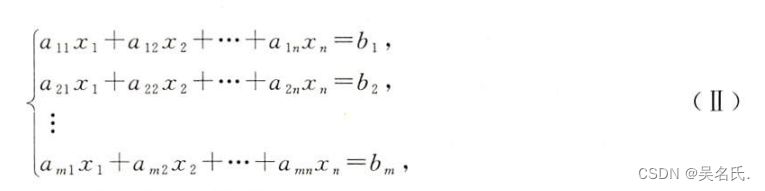

则方程组(I)(II)可以表示为如下向量形式:

向量的相关性与线性表示理论本质上就是以向量为工具对方程组理论进行描述
注意:
(1)设a1,a2,…,an为向量组,称 k1a1+k2a2+…+knan为向量组a1,a2,…,an的线性组合
(2)设a2,a2,…,an为向量组,b为一个向量,若存在一组数 k1,k2,…,kn,使得b=k1a1+k2a2+…+knan,称向量b可由向量组a1,a2,…,an线性表示
二、向量组相关性与线性表示的基本概念
①相关性
对齐次线性方程组
x1a1+x2a2+…+xnan=0 (*)
(1)若方程组()只有零解,即()成立当且仅当x1=x2=…=xn=0,称向量组a1,a2,…,an线性无关
(2)若方程组(*)有非零解,即存在不全为零的数 k1,k2,…,kn使得,k1a1+k2a2+…+knan=0,称向量组 a1,a2,…,az线性相关
②线性表示
对非齐次线性方程组
x1a1+x2a2+…+xnan=b (**)
(1)若方程组(**)有解,即存在常数k1,k2,…,kn,使得k1a1+k2a2+…+knan=b,称向量b可由向量组a1,a2,…,an线性表示;
(2)若方程组(**)无解,称向量b不可由向量组a1,a2,…,an线性表示
三、向量组相关性与线性表示的性质
性质1 向量组a1,a2,…,an线性相关的充分必要条件是向量组a1,a2,…,an中至少有一个向量可由其余向量线性表示
注意:
(1)一个向量线性相关的充分必要条件是该向量为零向量
(2)两个向量线性相关的充分必要条件是两个向量成比例
(3)含零向量的向量组一定线性相关
性质2 设a1,a2,…,an线性无关,则
(1)若a1,a2,…,an,b线性相关,则向量b可由a1,a2,…,an唯一线性表示
(2)a1,a2,…,an,b线性无关的充分必要条件是向量b不可由a1,a2,…,an线性表示
性质3 若一个向量组线性无关,则该向量组的任何部分向量组都线性无关
性质4 若向量组有一个部分向量组线性相关,则该向量组一定线性相关.
性质5 设a1,a2,…,an为n个n维向量,则a1,a2,…,an线性无关的充分必要条件是,|a1,a2,…,an|≠0
性质6 设a1,a2,…,an为n个m维向量,若m<n,则向量组a1,a2,…,an一定线性相关
注意:
(1)向量组中向量的个数对应齐次线性方程组未知数的个数,向量组中向量的个数越多,齐次线性方程组中未知数的个数就越多,齐次线性方程组产生自由变量的可能性也越大,从而齐次线性方程组有非零解的可能性增加,即向量组线性相关的可能性增加。故增加向量的个数后线性相关的可能性增加
(2)向量组中向量的维数对应齐次线性方程组方程的个数,维数越多,齐次线性方程组方程的个数越多,只有零解的可能性增加,即向量组线性无关的可能性增加,故增加向量的维数后线性无关的可能性增加
性质7 设向量组a’1,a’2,…,a’n为向量组a1,a2,…,an的扩充向量组(即添加维数后的向量组),若向量组a1,a2,…,an线性无关,则向量组a’1,a’2,…,a’n线性无关,反之不对
性质8 设a1,a2,…,an为两两正交的非零向量组,则a1,a2,…,an线性无关,反之不对.
第三节 向量组等价、向量组的极大线性无关组与向量组的秩
一、基本概念
①向量组等价

注意:等价的两个向量组所含的向量个数可能不同
②向量组的极大线性无关组与向量组的秩
设a1,a2,…,an为一组向量,若满足
(1)向量组a1,a2,…,an中存在r个向量线性无关;
(2)任意r+1个向量(不一定存在)一定线性相关,
称广个线性无关的向量组为向量组a1,a2,…,an的极大线性无关组,极大线性无关组中所含向量的个数称为向量组的秩.
注意:

二、向量组秩的性质

第四节 n维向量空间
一、基本概念
①n维向量空间
所有n维向量连同向量的加法及数与向量的乘法运算称为n维向量空间,记为R^n
②基
设Rn为n维向量空间,设a1,a2,…,an为Rn中的n个向量,若满足:
(1)a1,a2,…,an线性无关
(2)对任意的β∈R^n,β都可由向量组a1,a2,…,an线性表示
则称a1,a2,…,an为维向量空间R^n的基.
特别地,设a1,a2,…,an为n维向量空间R^n的基,如满足:
(1)a1,a2,…,an两两正交
(2)a1,a2,…,an都是单位向量
称a1,a2,…,an为n维向量空间R^n的正交规范基
③向量在基下的坐标
设a1,a2,…,an为n维向量空间Rn的基,β∈Rn,若B=k1a1+k2a2+…+knan,称(k1,k2,…,kn)为向量B在基a1,a2,…,an下的坐标
④过渡矩阵
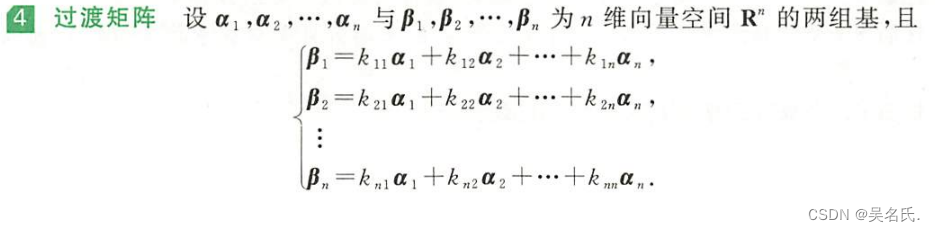

二、基本性质

相关文章:

线性代数基础【3】向量
第一节 向量的概念与运算 一、基本概念 ①向量 ②向量的模(长度) ③向量的单位化 ④向量的三则运算 ⑤向量的内积 二、向量运算的性质 (一)向量三则运算的性质 α β β αα (β γ) (α β) γk (α β) kα kβ(k l) α kα lα (二)向量内积运…...

Spring Boot + MinIO 实现文件切片极速上传技术
文章目录 1. 引言2. 文件切片上传简介3. 技术选型3.1 Spring Boot3.2 MinIO 4. 搭建Spring Boot项目5. 集成MinIO5.1 配置MinIO连接信息5.2 MinIO配置类 6. 文件切片上传实现6.1 控制器层6.2 服务层6.3 文件切片上传逻辑 7. 文件合并逻辑8. 页面展示9. 性能优化与拓展9.1 性能优…...

uniapp中如何使用image图片
当在UniApp中使用图片时,可以通过<image>标签将图片显示在页面上。这个标签可以指定src属性来引用图片,并且可以通过mode属性来设置图片的显示模式。除此之外,还可以利用click事件来实现图片的点击事件。在编写代码时,要注意…...

docker-compose 安装gitlab
写在前面的话:docker-compose的文件是通用的,因此可以切换任意版本的gitlab的镜像版本。 往期docker-compose部署系列如: docker-compose语法格式docker-compose部署openldapdocker-compose 安装Sonar并集成gitlab 文章目录 1. 参考文档2. 环…...
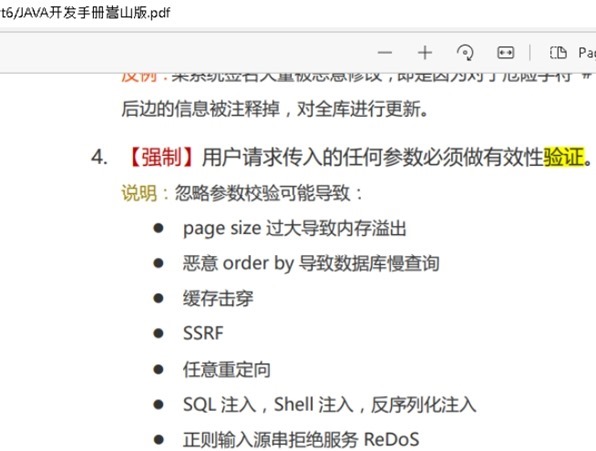
到底是前端验证还是后端验证
背景 软件应用研发中, 前端验证还是后端验证这是意识与认知问题。鉴于某些入门同学还不清楚,我们再来看下: 一. 从软件行业来自国外 Q: 前端验证和后端验证都是对同一个数据的验证,有什么区别? A: 二者的目的不同&…...

AlignBench:量身打造的中文大语言模型对齐评测
对齐(Alignment),是指大语言模型(LLM)与人类意图的一致性。换言之,就是让LLM生成的结果更加符合人类的预期,包括遵循人类的指令,理解人类的意图,进而能产生有帮助的回答等…...

asp.net core 教程
asp.net core 教程 写在前面新建项目Get和PostGETPOST MVC-模型控制视图如何通俗理解MVCMVC架构---文件夹详解Connected ServicesPropertieswwwroot依赖项ControllersModelsViews 代码实例 API模型(前后端分离)前端代码后端代码 文件配置优先级优先级顺序…...

概率论1:下象棋问题(3.5)
每日小语 时刻望着他人的眼色行事,是腾飞不了的。自己怎么想就积极地去做,这是需要胆量的。——广中平佑 题目 甲、乙二人下象棋, 每局甲胜的概率为a,乙胜的概率为b. 为简化问题,设没有和局的情况,这意味着a b1. 设想…...

LLM调研笔记
这里写目录标题 LLM调研1. 外挂知识库2. 微调数据prompting和fine-tuning的对比 3. NLP的发展4. 大语言模型的涌现能力5. 大模型的几个关键技术6. 数据预处理7. 主流架构8. 模型训练9. 大模型的微调10. 大模型的使用11. 大模型的评估 LLM调研 大模型的不足:在特定的…...
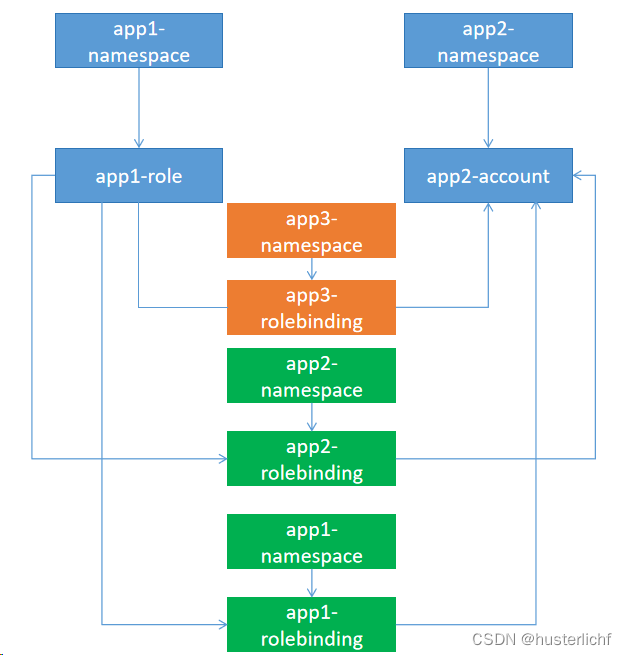
K8S----RBAC
一、角色、绑定、用户 1、 Role 与ClusterRole 1、Role 总是要在一个命名空间中设置权限,当需要创建一个Role的时候必须指定命名空间; 2、ClusterRole 是非命名空间范围的,不受命名空间局限 2 、RoleBinding 与ClusterRoleBinding 1、RoleBinding 是受命名空间限制的 2、…...
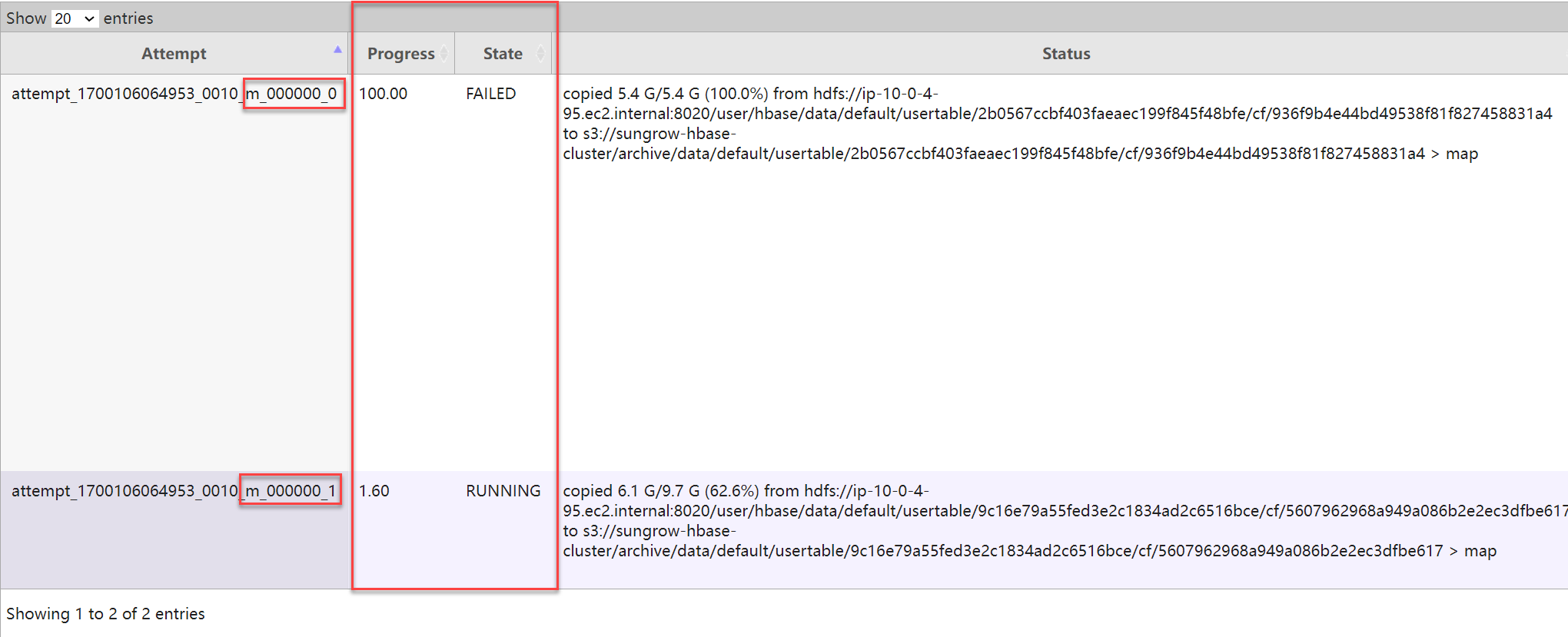
HBase 超大表迁移、备份、还原、同步演练手册:全量快照 + 实时同步(Snapshot + Replication)不停机迁移方案
博主历时三年精心创作的《大数据平台架构与原型实现:数据中台建设实战》一书现已由知名IT图书品牌电子工业出版社博文视点出版发行,点击《重磅推荐:建大数据平台太难了!给我发个工程原型吧!》了解图书详情,…...

统计直线上2个点的分布占比
直线上有6个格子,向格子里扔2个石子,共有5种可能。 1 1 0 0 0 0 0 1 1 0 0 0 0 0 1 1 0 0 0 0 0 1 1 0 0 0 0 0 1 1 第1种两个石子是连着的,共有5个 1 0 1 0 0 0 0 1 0 1 0 0 0 0 1 0 1 0 …...
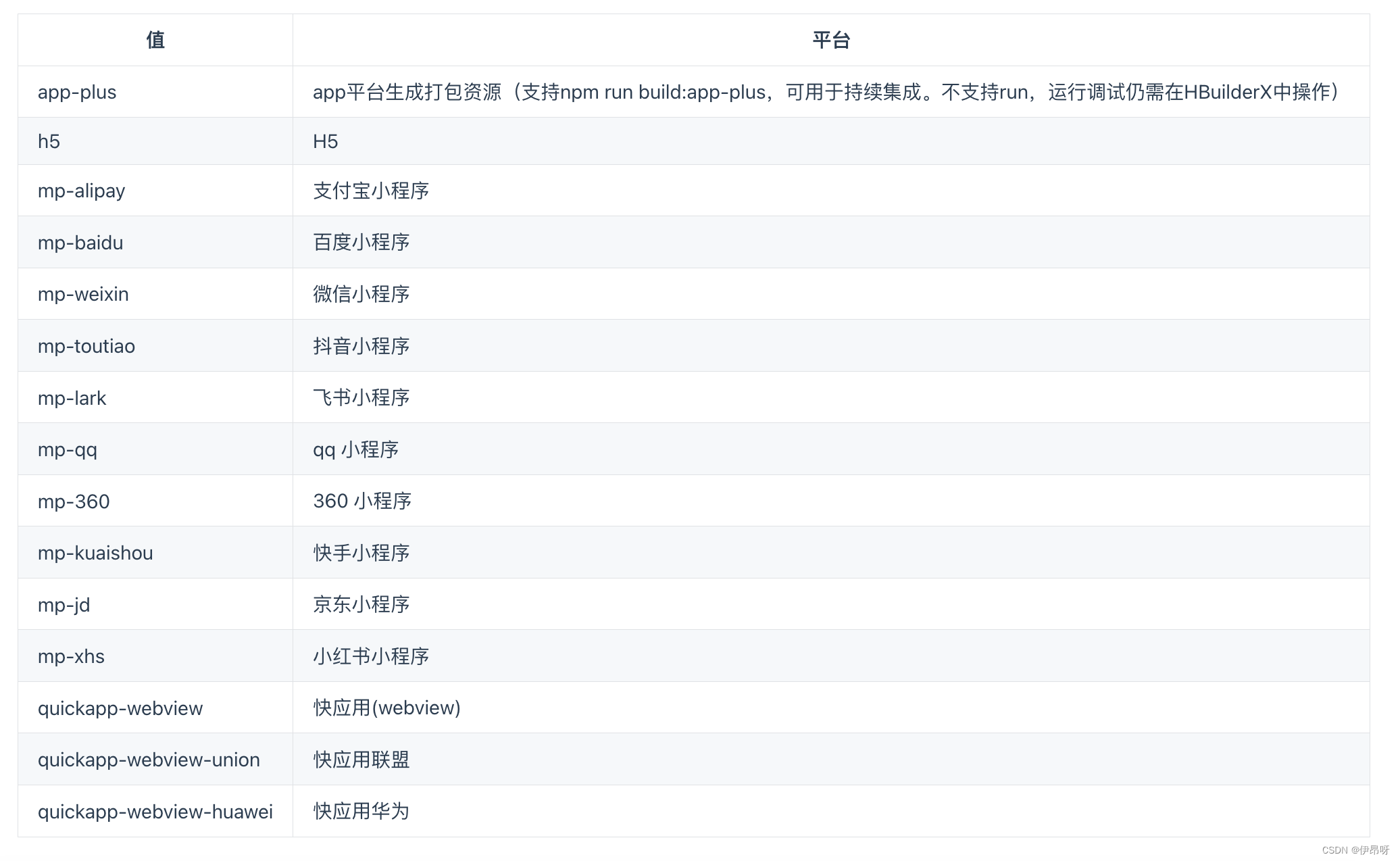
uniapp创建/运行/发布项目
1、产生背景----跨平台应用框架 在移动端各大App盛行的时代,App之间的竞争也更加激烈,他们执着于让一个应用可以做多个事情 所以就应运而生了小程序,微信小程序、支付宝小程序、抖音小程序等等基于App本身的内嵌类程序。 但是各大App他不可…...

洛谷 P2367 语文成绩 刷题笔记
P2367 语文成绩 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn) 差分 令a[i]为b[i]数组的前缀和 a[n]b[1]b[2]b[3].....b[n]; a[n-1]b[1]b[2]b[3].....b[n-1]; 构造差分数组 b[i]a[i]-a[i-1]; 有什么好处 当我们想对a[l]--a[r]范围内所有数据加上一个数x 不必循环 for(i…...
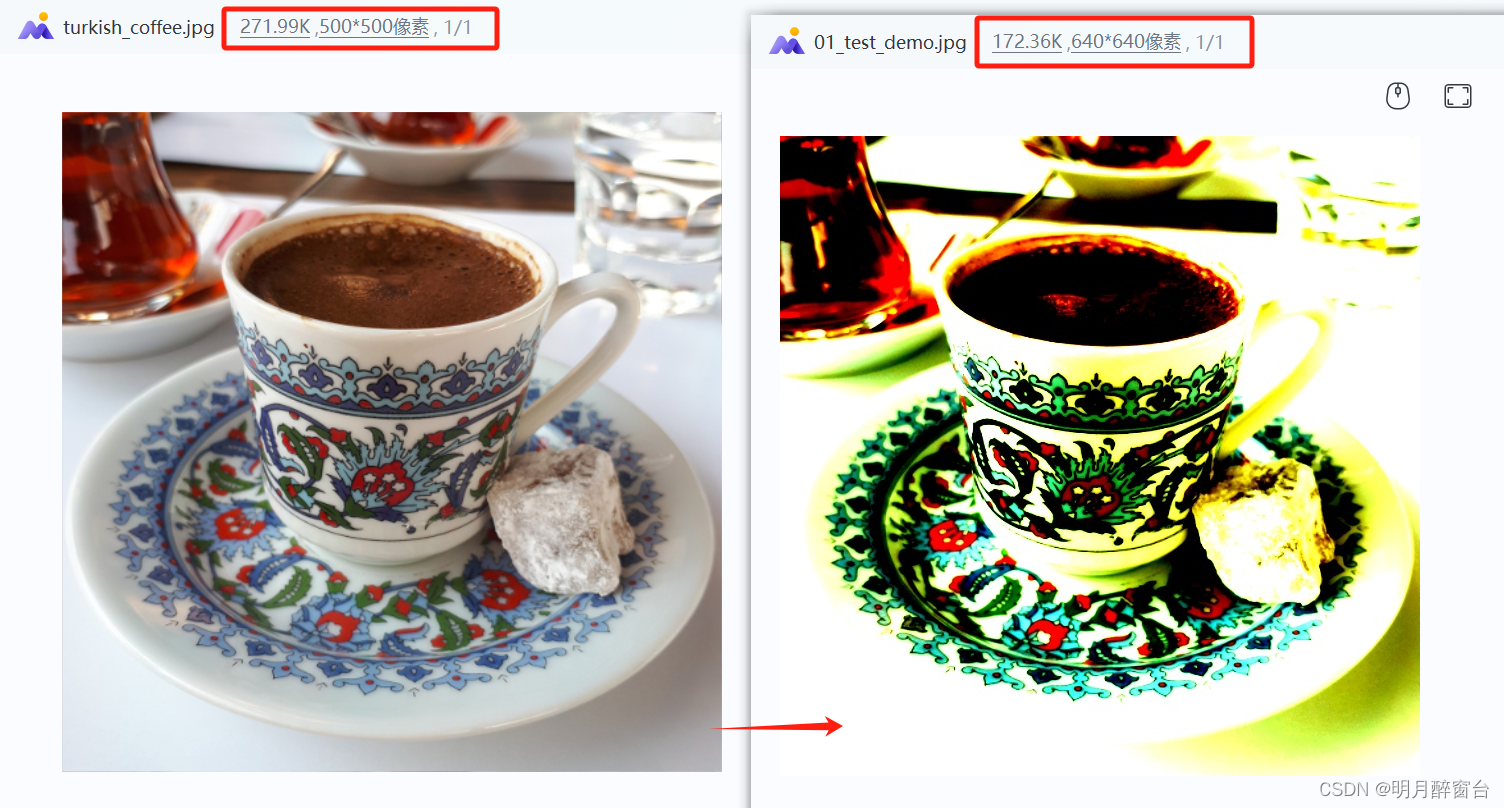
Opencv_CUDA实现推理图像前处理与后处理
Opencv_CUDA实现推理图像前处理与后处理 通过trt 或者 openvino部署深度学习算法时,往往会通过opencv的Mat及算法将图像转换为固定的格式作为输入openvino图像的前后处理后边将在单独的文章中写出今晚空闲搜了一些opencv_cuda的使用方法,在此总结一下前…...

Android.bp 和 Android.mk 的对应关系
参考 Soong 构建系统 Android.mk 转为 Android.bp 没有分支、循环等流程控制的简单的 Android.mk ,可以通过 androidmk 命令转化为 Android.bp source 、lunch 之后执行即可。 androidmk Android.mk > Android.bp对应关系 Android 13 ,build/soon…...

力扣-收集足够苹果的最小花园周长[思维+组合数]
题目链接 题意: 给你一个用无限二维网格表示的花园,每一个 整数坐标处都有一棵苹果树。整数坐标 (i, j) 处的苹果树有 |i| |j| 个苹果。 你将会买下正中心坐标是 (0, 0) 的一块 正方形土地 ,且每条边都与两条坐标轴之一平行。 给你一个整…...

【C语言】自定义类型:结构体深入解析(三)结构体实现位段最终篇
文章目录 📝前言🌠什么是位段?🌉 位段的内存分配🌉VS怎么开辟位段空间呢?🌉位段的跨平台问题🌠 位段的应⽤🌠位段使⽤的注意事项🚩总结 📝前言 本…...
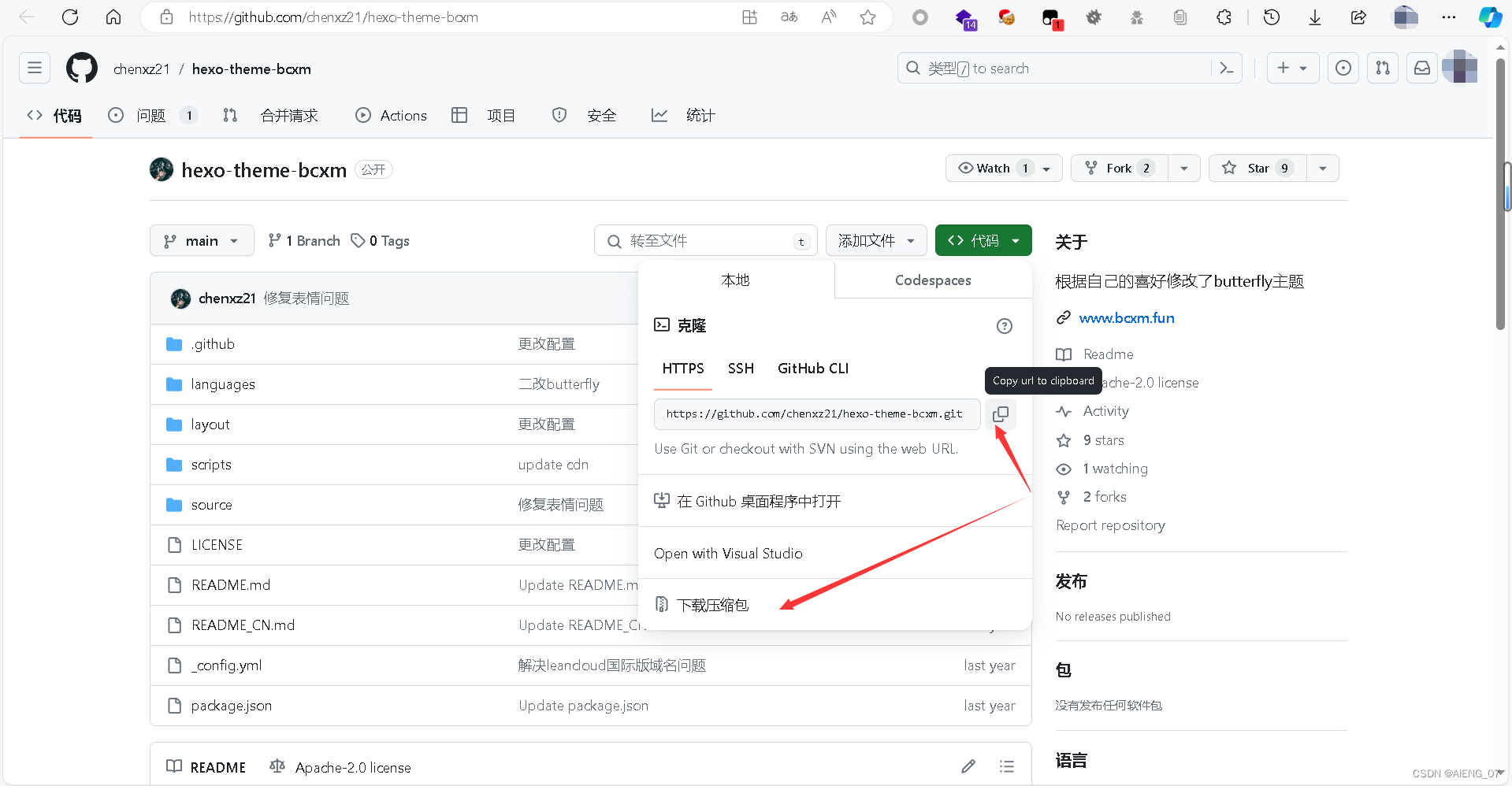
基于Hexo+GitHub Pages 的个人博客搭建
基于HexoGitHub Pages 的个人博客搭建 步骤一:安装 Node.js 和 Git步骤二:创建Github Pages 仓库步骤二:安装 Hexo步骤三:创建 Hexo 项目步骤四:配置 Hexo步骤五:创建新文章步骤六:生成静态文件…...

7. 结构型模式 - 代理模式
亦称: Proxy 意图 代理模式是一种结构型设计模式, 让你能够提供对象的替代品或其占位符。 代理控制着对于原对象的访问, 并允许在将请求提交给对象前后进行一些处理。 问题 为什么要控制对于某个对象的访问呢? 举个例子ÿ…...

iOS 26 携众系统重磅更新,但“苹果智能”仍与国行无缘
美国西海岸的夏天,再次被苹果点燃。一年一度的全球开发者大会 WWDC25 如期而至,这不仅是开发者的盛宴,更是全球数亿苹果用户翘首以盼的科技春晚。今年,苹果依旧为我们带来了全家桶式的系统更新,包括 iOS 26、iPadOS 26…...

家政维修平台实战20:权限设计
目录 1 获取工人信息2 搭建工人入口3 权限判断总结 目前我们已经搭建好了基础的用户体系,主要是分成几个表,用户表我们是记录用户的基础信息,包括手机、昵称、头像。而工人和员工各有各的表。那么就有一个问题,不同的角色…...

屋顶变身“发电站” ,中天合创屋面分布式光伏发电项目顺利并网!
5月28日,中天合创屋面分布式光伏发电项目顺利并网发电,该项目位于内蒙古自治区鄂尔多斯市乌审旗,项目利用中天合创聚乙烯、聚丙烯仓库屋面作为场地建设光伏电站,总装机容量为9.96MWp。 项目投运后,每年可节约标煤3670…...
 自用)
css3笔记 (1) 自用
outline: none 用于移除元素获得焦点时默认的轮廓线 broder:0 用于移除边框 font-size:0 用于设置字体不显示 list-style: none 消除<li> 标签默认样式 margin: xx auto 版心居中 width:100% 通栏 vertical-align 作用于行内元素 / 表格单元格ÿ…...

python执行测试用例,allure报乱码且未成功生成报告
allure执行测试用例时显示乱码:‘allure’ �����ڲ����ⲿ���Ҳ���ǿ�&am…...

Kafka主题运维全指南:从基础配置到故障处理
#作者:张桐瑞 文章目录 主题日常管理1. 修改主题分区。2. 修改主题级别参数。3. 变更副本数。4. 修改主题限速。5.主题分区迁移。6. 常见主题错误处理常见错误1:主题删除失败。常见错误2:__consumer_offsets占用太多的磁盘。 主题日常管理 …...

十九、【用户管理与权限 - 篇一】后端基础:用户列表与角色模型的初步构建
【用户管理与权限 - 篇一】后端基础:用户列表与角色模型的初步构建 前言准备工作第一部分:回顾 Django 内置的 `User` 模型第二部分:设计并创建 `Role` 和 `UserProfile` 模型第三部分:创建 Serializers第四部分:创建 ViewSets第五部分:注册 API 路由第六部分:后端初步测…...

【Post-process】【VBA】ETABS VBA FrameObj.GetNameList and write to EXCEL
ETABS API实战:导出框架元素数据到Excel 在结构工程师的日常工作中,经常需要从ETABS模型中提取框架元素信息进行后续分析。手动复制粘贴不仅耗时,还容易出错。今天我们来用简单的VBA代码实现自动化导出。 🎯 我们要实现什么? 一键点击,就能将ETABS中所有框架元素的基…...

ubuntu22.04 安装docker 和docker-compose
首先你要确保没有docker环境或者使用命令删掉docker sudo apt-get remove docker docker-engine docker.io containerd runc安装docker 更新软件环境 sudo apt update sudo apt upgrade下载docker依赖和GPG 密钥 # 依赖 apt-get install ca-certificates curl gnupg lsb-rel…...
:电商转化率优化与网站性能的底层逻辑)
精益数据分析(98/126):电商转化率优化与网站性能的底层逻辑
精益数据分析(98/126):电商转化率优化与网站性能的底层逻辑 在电子商务领域,转化率与网站性能是决定商业成败的核心指标。今天,我们将深入解析不同类型电商平台的转化率基准,探讨页面加载速度对用户行为的…...
