C语言—每日选择题—Day63
指针相关博客
打响指针的第一枪:指针家族-CSDN博客
深入理解:指针变量的解引用 与 加法运算-CSDN博客
第一题
1. 设C语言中,一个int型数据在内存中占2个字节,则unsigned int型数据的取值范围为
A:0~255
B:0~3267
C:0~65535
D:0~2147483647
答案及解析 C
unsigned int 是无符号的类型,二进制位中最高位是数值位
所以最大值:1111 1111 1111 1111 = 65535
第二题
2. 执行下列程序:
#define MA(x, y) (x*y)
i = 5;
i = MA(i,i+1)-7;变量i的值应为( )
A:30
B:19
C:23
D:1
答案及解析 B
define宏定义是替换
i = MA(i, i + 1) - 7 = i * i + 1 - 7 = 19
第三题
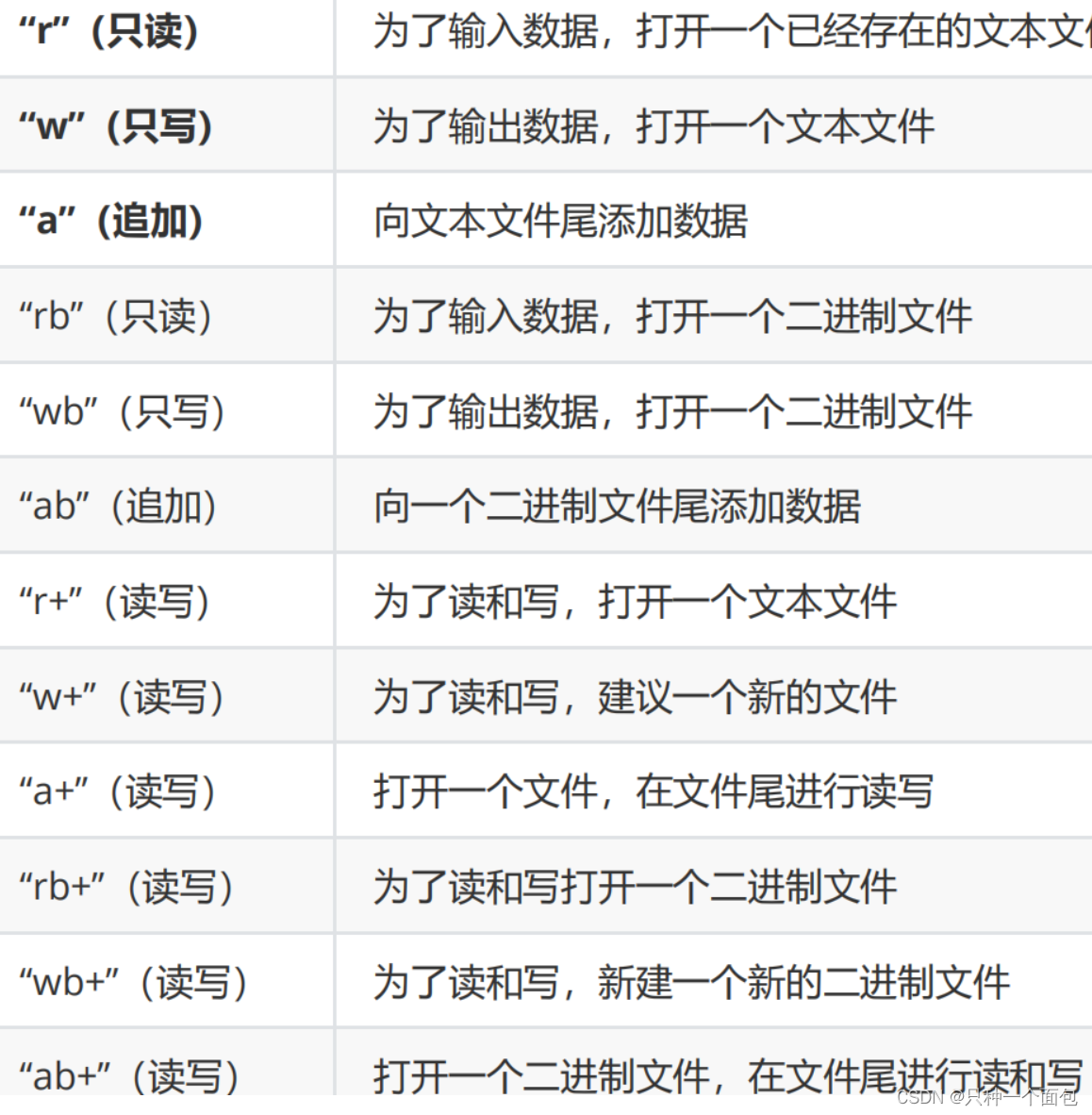
3. 用fopen函数打开一个新的二进制文件,该文件既能读也能写,则文件方字符串应是()
A:"ab++”
B:"wb+"
C:"rb+"
D:"ab"
答案及解析 B
第四题
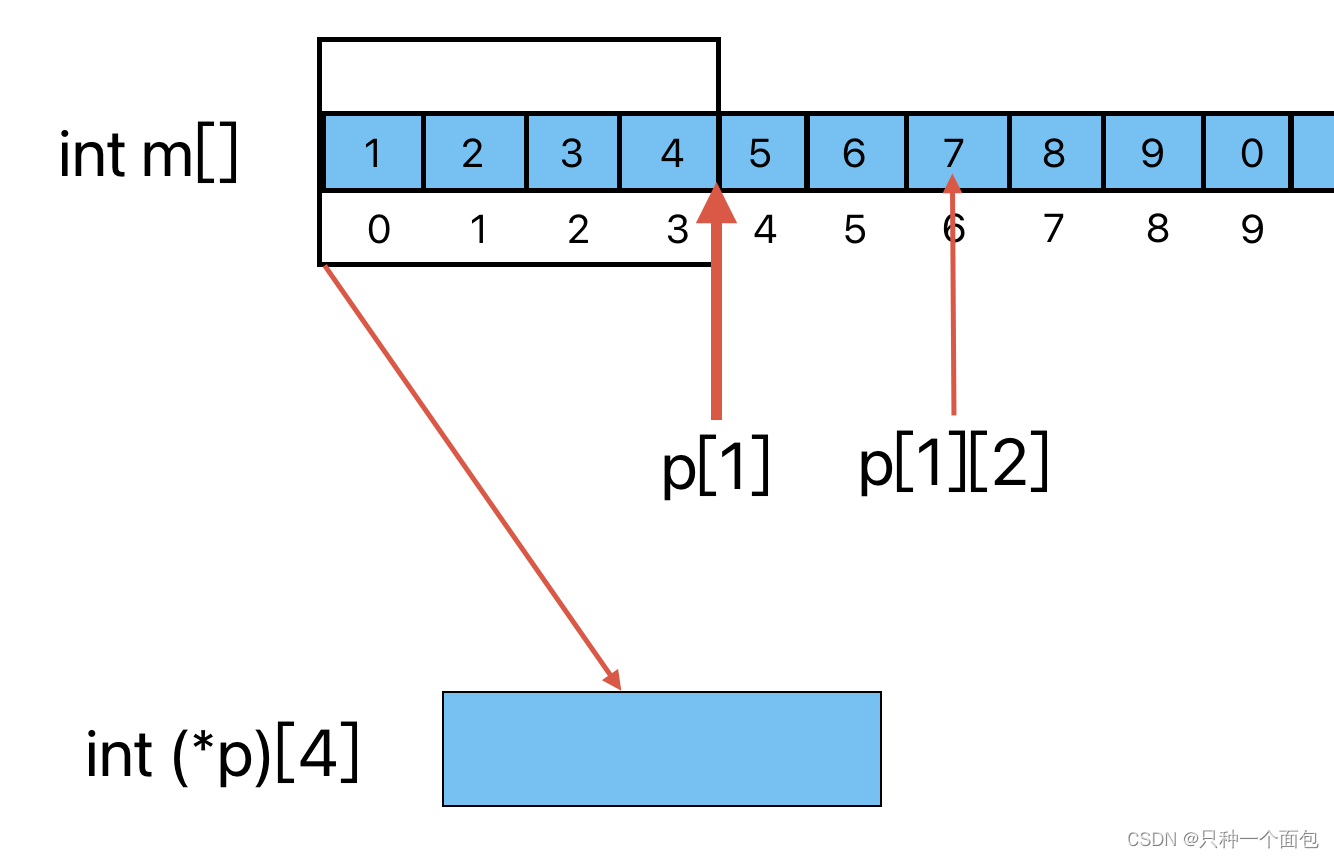
4. 请问下列代码的输出是多少()
#include <stdio.h>
int main()
{int m[] = {1, 2, 3, 4, 5, 6, 7, 8, 9, 0};int(*p)[4] = (int(*)[4])m;printf("%d", p[1][2]);return 0;
}A:7
B:3
C:8
D:4
答案及解析 A
本题是将指针数组和一维数组进行联系,将一维数组m强制转换为指针数组类型,数据范围是4个元素,所以p[1][2] 相当于 *(*(p + 1) + 2),先向后移动4个元素大小,再移动两个元素大小。
第五题
5. 有以下定义: char a; int b; float c; double d;则表达式a*b+d-c值的类型为:
A:float
B:int
C:char
D:double
答案及解析 D
本题涉及到隐式类型转换隐式类型转换(整型提升和截断)、强制类型转换的总结-CSDN博客
相关文章:

C语言—每日选择题—Day63
指针相关博客 打响指针的第一枪:指针家族-CSDN博客 深入理解:指针变量的解引用 与 加法运算-CSDN博客 第一题 1. 设C语言中,一个int型数据在内存中占2个字节,则unsigned int型数据的取值范围为 A:0~255 B:0…...

Mac_通过chmod处理文件权限
chmod 简介 chmod 是一个 Unix 和类 Unix 系统中的命令,用于更改文件或目录的权限。chmod 的名称来源于 “change mode”,它允许用户修改文件或目录的读取(read)、写入(write)和执行(execute&a…...

实战指南:使用 Spring Cloud Stream 集成 Kafka 构建高效消息驱动微服务
实战指南:使用 Spring Cloud Stream 集成 Kafka 构建高效消息驱动微服务 视频地址: Stream为什么被引入-尚硅谷SCS-1-内容介绍-图灵诸葛 官方文档: Spring Cloud Stream 什么是 Spring Cloud Stream? Spring Cloud Stream(SCS) 是一个用于构…...

线性代数基础【3】向量
第一节 向量的概念与运算 一、基本概念 ①向量 ②向量的模(长度) ③向量的单位化 ④向量的三则运算 ⑤向量的内积 二、向量运算的性质 (一)向量三则运算的性质 α β β αα (β γ) (α β) γk (α β) kα kβ(k l) α kα lα (二)向量内积运…...

Spring Boot + MinIO 实现文件切片极速上传技术
文章目录 1. 引言2. 文件切片上传简介3. 技术选型3.1 Spring Boot3.2 MinIO 4. 搭建Spring Boot项目5. 集成MinIO5.1 配置MinIO连接信息5.2 MinIO配置类 6. 文件切片上传实现6.1 控制器层6.2 服务层6.3 文件切片上传逻辑 7. 文件合并逻辑8. 页面展示9. 性能优化与拓展9.1 性能优…...

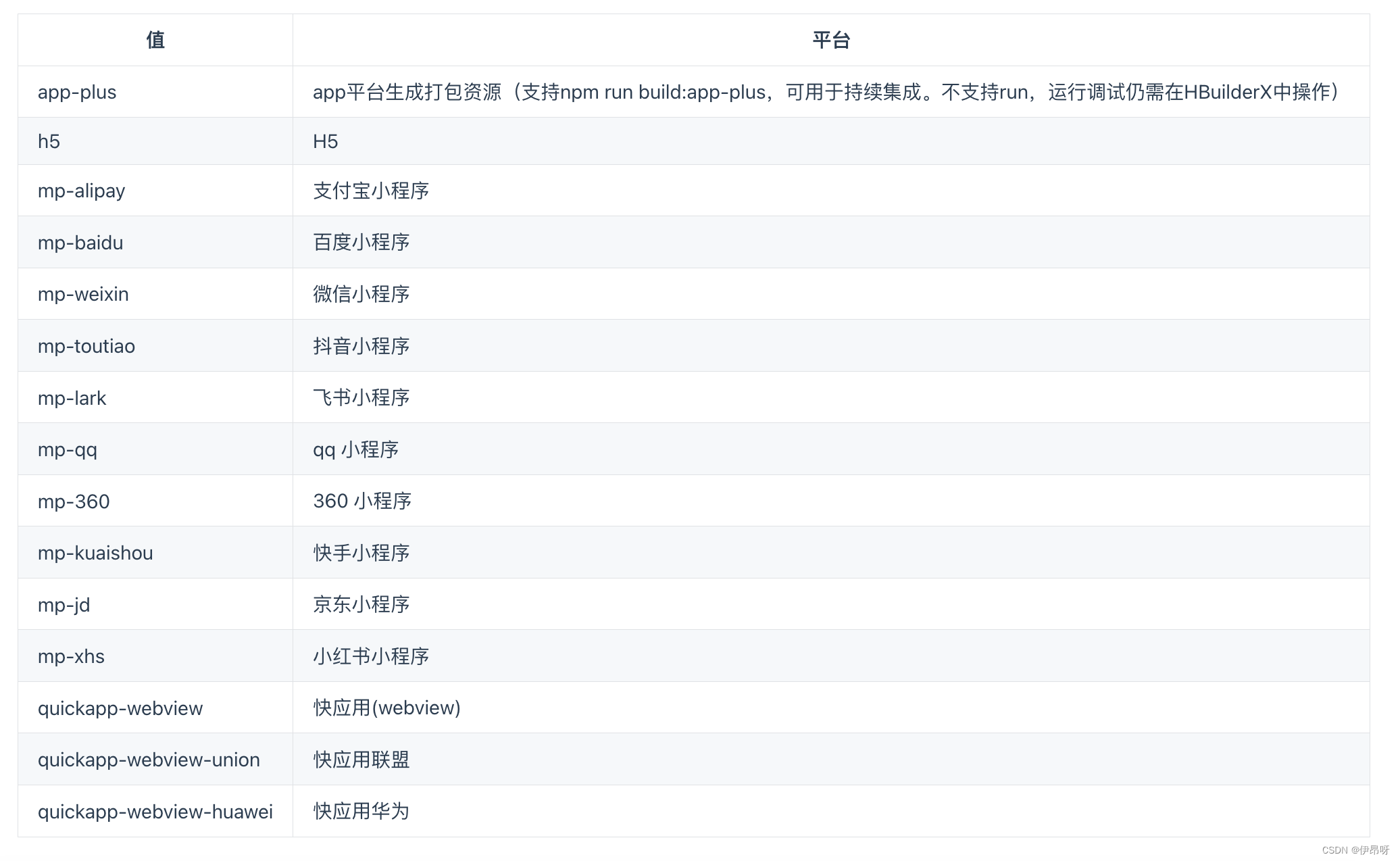
uniapp中如何使用image图片
当在UniApp中使用图片时,可以通过<image>标签将图片显示在页面上。这个标签可以指定src属性来引用图片,并且可以通过mode属性来设置图片的显示模式。除此之外,还可以利用click事件来实现图片的点击事件。在编写代码时,要注意…...

docker-compose 安装gitlab
写在前面的话:docker-compose的文件是通用的,因此可以切换任意版本的gitlab的镜像版本。 往期docker-compose部署系列如: docker-compose语法格式docker-compose部署openldapdocker-compose 安装Sonar并集成gitlab 文章目录 1. 参考文档2. 环…...
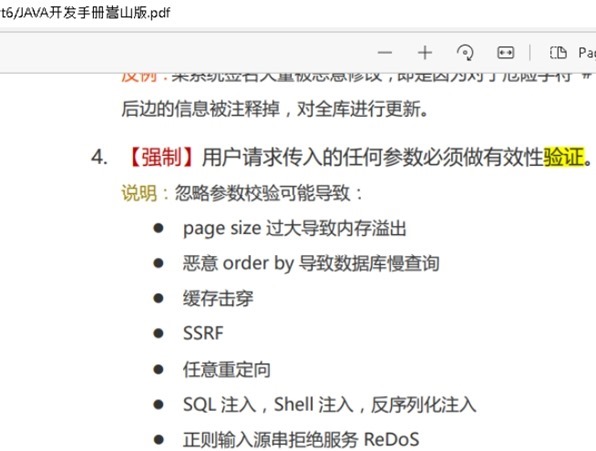
到底是前端验证还是后端验证
背景 软件应用研发中, 前端验证还是后端验证这是意识与认知问题。鉴于某些入门同学还不清楚,我们再来看下: 一. 从软件行业来自国外 Q: 前端验证和后端验证都是对同一个数据的验证,有什么区别? A: 二者的目的不同&…...

AlignBench:量身打造的中文大语言模型对齐评测
对齐(Alignment),是指大语言模型(LLM)与人类意图的一致性。换言之,就是让LLM生成的结果更加符合人类的预期,包括遵循人类的指令,理解人类的意图,进而能产生有帮助的回答等…...

asp.net core 教程
asp.net core 教程 写在前面新建项目Get和PostGETPOST MVC-模型控制视图如何通俗理解MVCMVC架构---文件夹详解Connected ServicesPropertieswwwroot依赖项ControllersModelsViews 代码实例 API模型(前后端分离)前端代码后端代码 文件配置优先级优先级顺序…...

概率论1:下象棋问题(3.5)
每日小语 时刻望着他人的眼色行事,是腾飞不了的。自己怎么想就积极地去做,这是需要胆量的。——广中平佑 题目 甲、乙二人下象棋, 每局甲胜的概率为a,乙胜的概率为b. 为简化问题,设没有和局的情况,这意味着a b1. 设想…...

LLM调研笔记
这里写目录标题 LLM调研1. 外挂知识库2. 微调数据prompting和fine-tuning的对比 3. NLP的发展4. 大语言模型的涌现能力5. 大模型的几个关键技术6. 数据预处理7. 主流架构8. 模型训练9. 大模型的微调10. 大模型的使用11. 大模型的评估 LLM调研 大模型的不足:在特定的…...
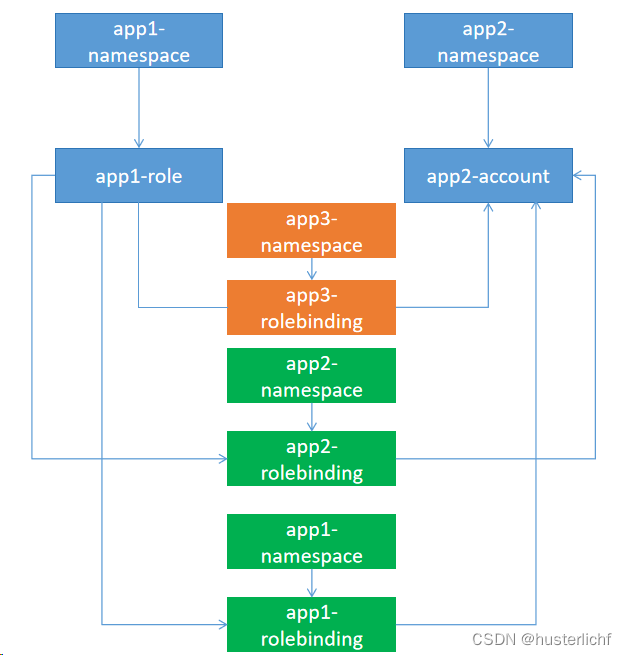
K8S----RBAC
一、角色、绑定、用户 1、 Role 与ClusterRole 1、Role 总是要在一个命名空间中设置权限,当需要创建一个Role的时候必须指定命名空间; 2、ClusterRole 是非命名空间范围的,不受命名空间局限 2 、RoleBinding 与ClusterRoleBinding 1、RoleBinding 是受命名空间限制的 2、…...
HBase 超大表迁移、备份、还原、同步演练手册:全量快照 + 实时同步(Snapshot + Replication)不停机迁移方案
博主历时三年精心创作的《大数据平台架构与原型实现:数据中台建设实战》一书现已由知名IT图书品牌电子工业出版社博文视点出版发行,点击《重磅推荐:建大数据平台太难了!给我发个工程原型吧!》了解图书详情,…...

统计直线上2个点的分布占比
直线上有6个格子,向格子里扔2个石子,共有5种可能。 1 1 0 0 0 0 0 1 1 0 0 0 0 0 1 1 0 0 0 0 0 1 1 0 0 0 0 0 1 1 第1种两个石子是连着的,共有5个 1 0 1 0 0 0 0 1 0 1 0 0 0 0 1 0 1 0 …...
uniapp创建/运行/发布项目
1、产生背景----跨平台应用框架 在移动端各大App盛行的时代,App之间的竞争也更加激烈,他们执着于让一个应用可以做多个事情 所以就应运而生了小程序,微信小程序、支付宝小程序、抖音小程序等等基于App本身的内嵌类程序。 但是各大App他不可…...

洛谷 P2367 语文成绩 刷题笔记
P2367 语文成绩 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn) 差分 令a[i]为b[i]数组的前缀和 a[n]b[1]b[2]b[3].....b[n]; a[n-1]b[1]b[2]b[3].....b[n-1]; 构造差分数组 b[i]a[i]-a[i-1]; 有什么好处 当我们想对a[l]--a[r]范围内所有数据加上一个数x 不必循环 for(i…...
Opencv_CUDA实现推理图像前处理与后处理
Opencv_CUDA实现推理图像前处理与后处理 通过trt 或者 openvino部署深度学习算法时,往往会通过opencv的Mat及算法将图像转换为固定的格式作为输入openvino图像的前后处理后边将在单独的文章中写出今晚空闲搜了一些opencv_cuda的使用方法,在此总结一下前…...

Android.bp 和 Android.mk 的对应关系
参考 Soong 构建系统 Android.mk 转为 Android.bp 没有分支、循环等流程控制的简单的 Android.mk ,可以通过 androidmk 命令转化为 Android.bp source 、lunch 之后执行即可。 androidmk Android.mk > Android.bp对应关系 Android 13 ,build/soon…...

力扣-收集足够苹果的最小花园周长[思维+组合数]
题目链接 题意: 给你一个用无限二维网格表示的花园,每一个 整数坐标处都有一棵苹果树。整数坐标 (i, j) 处的苹果树有 |i| |j| 个苹果。 你将会买下正中心坐标是 (0, 0) 的一块 正方形土地 ,且每条边都与两条坐标轴之一平行。 给你一个整…...

渲染学进阶内容——模型
最近在写模组的时候发现渲染器里面离不开模型的定义,在渲染的第二篇文章中简单的讲解了一下关于模型部分的内容,其实不管是方块还是方块实体,都离不开模型的内容 🧱 一、CubeListBuilder 功能解析 CubeListBuilder 是 Minecraft Java 版模型系统的核心构建器,用于动态创…...

el-switch文字内置
el-switch文字内置 效果 vue <div style"color:#ffffff;font-size:14px;float:left;margin-bottom:5px;margin-right:5px;">自动加载</div> <el-switch v-model"value" active-color"#3E99FB" inactive-color"#DCDFE6"…...

Cinnamon修改面板小工具图标
Cinnamon开始菜单-CSDN博客 设置模块都是做好的,比GNOME简单得多! 在 applet.js 里增加 const Settings imports.ui.settings;this.settings new Settings.AppletSettings(this, HTYMenusonichy, instance_id); this.settings.bind(menu-icon, menu…...

C++ 基础特性深度解析
目录 引言 一、命名空间(namespace) C 中的命名空间 与 C 语言的对比 二、缺省参数 C 中的缺省参数 与 C 语言的对比 三、引用(reference) C 中的引用 与 C 语言的对比 四、inline(内联函数…...

Python爬虫(一):爬虫伪装
一、网站防爬机制概述 在当今互联网环境中,具有一定规模或盈利性质的网站几乎都实施了各种防爬措施。这些措施主要分为两大类: 身份验证机制:直接将未经授权的爬虫阻挡在外反爬技术体系:通过各种技术手段增加爬虫获取数据的难度…...

自然语言处理——Transformer
自然语言处理——Transformer 自注意力机制多头注意力机制Transformer 虽然循环神经网络可以对具有序列特性的数据非常有效,它能挖掘数据中的时序信息以及语义信息,但是它有一个很大的缺陷——很难并行化。 我们可以考虑用CNN来替代RNN,但是…...

selenium学习实战【Python爬虫】
selenium学习实战【Python爬虫】 文章目录 selenium学习实战【Python爬虫】一、声明二、学习目标三、安装依赖3.1 安装selenium库3.2 安装浏览器驱动3.2.1 查看Edge版本3.2.2 驱动安装 四、代码讲解4.1 配置浏览器4.2 加载更多4.3 寻找内容4.4 完整代码 五、报告文件爬取5.1 提…...

Rapidio门铃消息FIFO溢出机制
关于RapidIO门铃消息FIFO的溢出机制及其与中断抖动的关系,以下是深入解析: 门铃FIFO溢出的本质 在RapidIO系统中,门铃消息FIFO是硬件控制器内部的缓冲区,用于临时存储接收到的门铃消息(Doorbell Message)。…...

代理篇12|深入理解 Vite中的Proxy接口代理配置
在前端开发中,常常会遇到 跨域请求接口 的情况。为了解决这个问题,Vite 和 Webpack 都提供了 proxy 代理功能,用于将本地开发请求转发到后端服务器。 什么是代理(proxy)? 代理是在开发过程中,前端项目通过开发服务器,将指定的请求“转发”到真实的后端服务器,从而绕…...

JVM虚拟机:内存结构、垃圾回收、性能优化
1、JVM虚拟机的简介 Java 虚拟机(Java Virtual Machine 简称:JVM)是运行所有 Java 程序的抽象计算机,是 Java 语言的运行环境,实现了 Java 程序的跨平台特性。JVM 屏蔽了与具体操作系统平台相关的信息,使得 Java 程序只需生成在 JVM 上运行的目标代码(字节码),就可以…...
