概率论中的 50 个具有挑战性的问题 [第 6 部分]:Chuck-a-Luck
一、说明

图片由作者使用 DALL-E 3 提供。
Chuck-a-Luck 是一种赌博游戏,经常在嘉年华会和赌场玩。玩家可以投注数字 1、2、3、4、5、6 中的任何一个。掷三个骰子。如果玩家的号码出现在骰子的一、二、三上,他将分别获得他原始赌注的一倍、两倍或三倍加上他自己的钱;否则,他将失去股份。
问题:玩家每单位赌注的预期损失是多少?
(实际上,玩家可以在几个数字上分配赌注,但每个这样的赌注都可以被视为一个单独的赌注。
二、问题分析:
合乎逻辑的方法是在六个数字中的每一个上放置一个单位赌注,导致玩家总共下注 6 个单位。有三种不同的可能情况:(1)三个骰子上的所有数字都不同,(2)骰子上的两个数字完全相同,(3)三个骰子上的所有数字都相同。让我们分别考虑每种情况。
情况(1):三个骰子上的所有数字都不同。
在这种情况下,您从三个中奖号码中赢了三个单位,但从三个输号码中损失了三个单位。因此,损失为 0 (3–3)。有多少种不同的方法可以得到三个不同的数字?它是 6 x 5 x 4 = 120 种方式。掷三个骰子的总可能结果是 6 x 6 x 6 = 216。
因此,在所有数字都不同的情况下,预期损失为 0 * (120/216) = 0。
情况(2):骰子上的两个数字完全相同。
在这种情况下,您赢得了三个单位,因为您从相同的数字中获得两个单位,从单个不同的数字中获得一个单位。但是,您从四个 (6-2) 失败数字中的四个单位中输掉。因此,每单位赌注的损失为 1/6 (4/6–3/6)。有多少种不同的方法可以得到两个相同的数字?它是 6 x 5 x 3 = 90 种方式。
因此,在两个数字完全相同的情况下,预期损失为 1/6 * (90/216) = 15/216。
情况(3):三个骰子上的所有数字都相同。
在这种情况下,您赢得了三个单位,因为您从相同的数字中获得三个单位。但是,您从五个 (6-1) 个失败数字中的五个单位中输掉了。因此,每单位赌注的损失为 2/6 (5/6–3/6)。有多少种不同的方法可以得到两个相同的数字?它只是 6 种方式。
因此,在所有三个数字都相同的情况下,预期损失为 2/6 * (6/216) = 1/108。
要计算玩家每单位赌注的预期损失,只需将所有三种情况的预期损失相加即可。
结合所有三种情况,玩家每单位赌注的预期损失为 0 + 15/216 + 1/108 = 0.079。
三、替代解决方案:
另一种方法是假设玩家只在一个数字上放置一个单位赌注。有四种不同的可能情况:(1)玩家的号码没有出现在三个骰子中的任何一个上,(2)玩家的号码出现在一个骰子上,(3)玩家的号码出现在两个骰子上,(4)玩家的号码出现在所有三个骰子上。让我们分别考虑每种情况。
情况(1):玩家的号码没有出现在三个骰子中的任何一个上。
发生这种情况的概率是 (5/6)³ = 125/216。
情况(2):玩家的号码出现在一个骰子上。
发生这种情况的概率是 (1/6) * (5/6)² * 3C1 = 25/72。
情况(3):玩家的号码出现在两个骰子上。
发生这种情况的概率是 (1/6)² * (5/6) * 3C2 = 5/72。
情况(4):玩家的号码出现在所有三个骰子上。
发生这种情况的概率为 (1/6)³ * 3C3 = 1/216。
通过将概率乘以每种情况的损失,我们得到与之前相同的结果(如下图所示)。
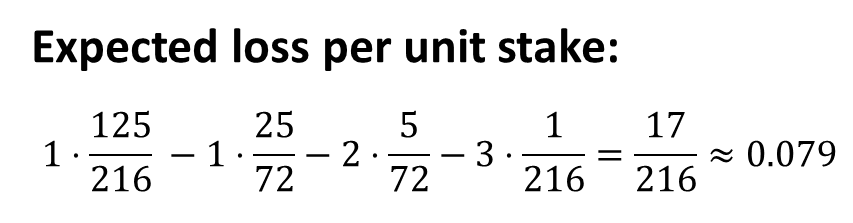
每单位股份的预期损失。
Python 代码:
import numpy as npn_trials = 10000000
choice = np.random.randint(1,7, size = (n_trials,1))
rolls = np.random.randint(1,7, size = (n_trials, 3))
count = np.sum(choice==rolls, axis=1)
mean_loss = (np.sum(count==0) + (-1)*np.sum(count))/n_trials
print(f'Expected loss per unit stake: {mean_loss:.3f}')# Output:
# Expected loss per unit stake: 0.079这就是这个运气🎲问题的全部内容。欢迎任何反馈或问题!该代码可在我的 Github 上找到。请继续关注本系列的下一部分!:)
相关文章:
概率论中的 50 个具有挑战性的问题 [第 6 部分]:Chuck-a-Luck
一、说明 我最近对与概率有关的问题产生了兴趣。我偶然读到了弗雷德里克莫斯特勒(Frederick Mosteller)的《概率论中的五十个具有挑战性的问题与解决方案》)一书。我认为创建一个系列来讨论这些可能作为面试问题出现的迷人问题会很有趣。每篇…...

windows搭建MySQL主从补充说明
这3种情况是在HA切换时,由于是异步复制,且sync_binlog0,会造成一小部分binlog没接收完导致同步报错。 第一种:在master上删除一条记录,而slave上找不到。 第二种:主键重复。在slave已经有该记录ÿ…...

Python:GUI Tkinter
GUI编程 GUI编程(Graphical User Interface Programming)指的是用于创建图形用户界面的程序设计。这种界面采用图形方式显示信息,让用户可以通过图形化的方式与程序进行交互,而不是仅仅通过文本命令。GUI编程使得软件更加直观易用…...

制作一个可以离线安装的Visual Studio安装包
须知 前提条件,需要电脑可以正常上网且网速还行,硬盘可以空间容量足够大,怎么判断容量够用?由组件数量的多少来决定。Visual Studio 频道和发布节奏 https://learn.microsoft.com/zh-cn/visualstudio/productinfo/release-rhythm…...
机器学习——决策树(三)
【说明】文章内容来自《机器学习——基于sklearn》,用于学习记录。若有争议联系删除。 1、案例一 决策树用于是否赖床问题。 采用决策树进行分类,要经过数据采集、特征向量化、模型训练和决策树可视化4个步骤。 赖床数据链接:https://pan…...
模型量化之AWQ和GPTQ
什么是模型量化 模型量化(Model Quantization)是一种通过减少模型参数表示的位数来降低模型计算和存储开销的技术。一般来说,模型参数在深度学习模型中以浮点数(例如32位浮点数)的形式存储,而模型量化可以…...
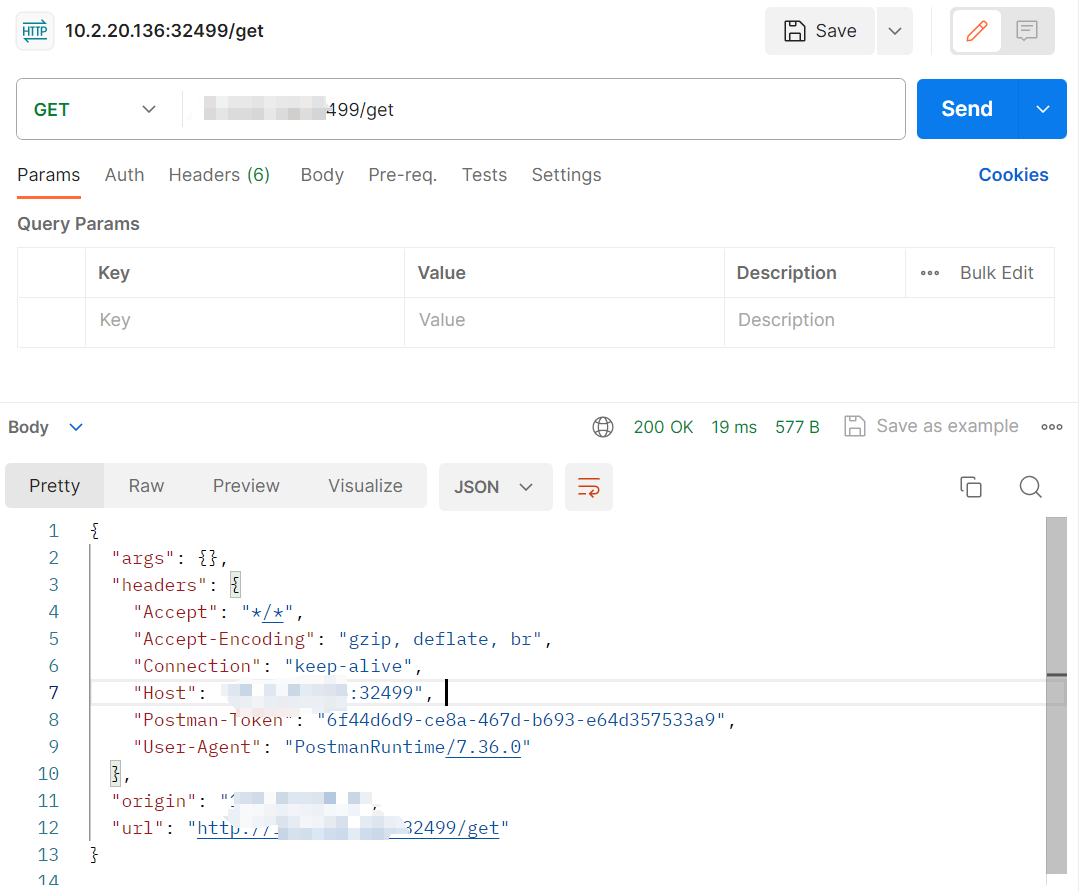
一个简单的 HTTP 请求和响应服务——httpbin
拉取镜像 docker pull kennethreitz/httpbin:latest 查看本地是否存在存在镜像 docker images | grep kennethreitz/httpbin:latest 创建 deployment,指定镜像 apiVersion: apps/v1 kind: Deployment metadata:labels:app: httpbinname: mm-httpbinnamespace: mm-…...
赛题第3套)
2024黑龙江省职业院校技能大赛暨国赛选拔赛应用软件系统开发赛项(高职组)赛题第3套
2024黑龙江省职业院校技能大赛暨国赛选拔赛 应用软件系统开发赛项(高职组) 赛题第3套 目录: 需要竞赛源码资料可以私信博主。 竞赛说明 模块一:系统需求分析 任务1:制造执行MES—质量管理—来料检验(…...

云原生Kubernetes系列 | Kubernetes Secret及ConfigMap
云原生Kubernetes系列 | Kubernetes Secret及Configmap 1. Secret及Configmap使用背景简介2. Secret2.1. Secret创建方式2.1.1. 命令行方式2.1.2. 文件方式2.1.3. 变量方式2.1.4. YAML文件方式2.2. Secret使用方式2.2.1. 用于传递配置文件2.2.3. 用于传递变量3. ConfigMap1. Se…...

dev express 15.2图表绘制性能问题
dev express 15.2 绘制曲线 前端代码 <dxc:ChartControl Grid.Row"1"><dxc:XYDiagram2D EnableAxisXNavigation"True"><dxc:LineSeries2D x:Name"series" CrosshairLabelPattern"{}{A} : {V:F2}"/></dxc:XYDi…...
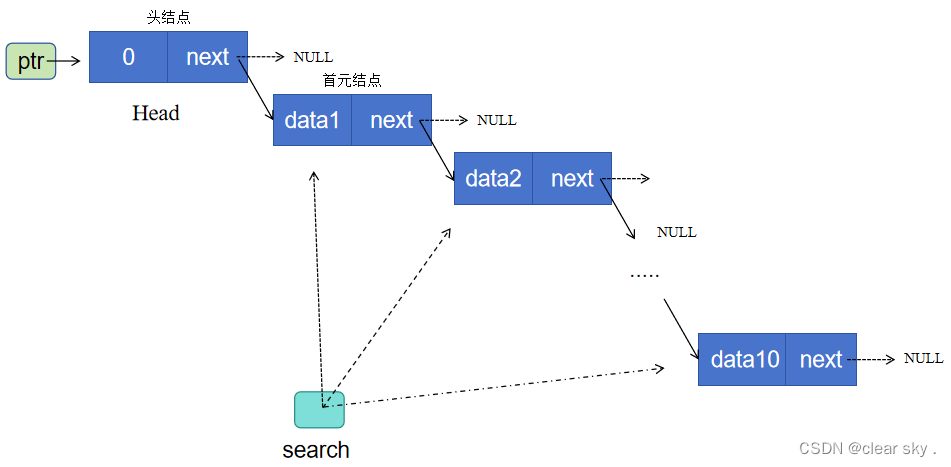
单链表的创建,插入及删除(更新ing)
1.单链表创建 ptr为头指针,指向头结点地址,即该指针变量的值为头结点地址; mov为一个辅助指针,用于将链表尾节点的指针域next指向新增节点的地址. search为一个辅助指针,用于遍历链表各节点地址,打印各节…...
C#/WPF 播放音频文件
C#播放音频文件的方式: 播放系统事件声音使用System.Media.SoundPlayer播放wav使用MCI Command String多媒体设备程序接口播放mp3,wav,avi等使用WindowsMediaPlayer的COM组件来播放(可视化)使用DirectX播放音频文件使用Speech播放(朗读器&am…...
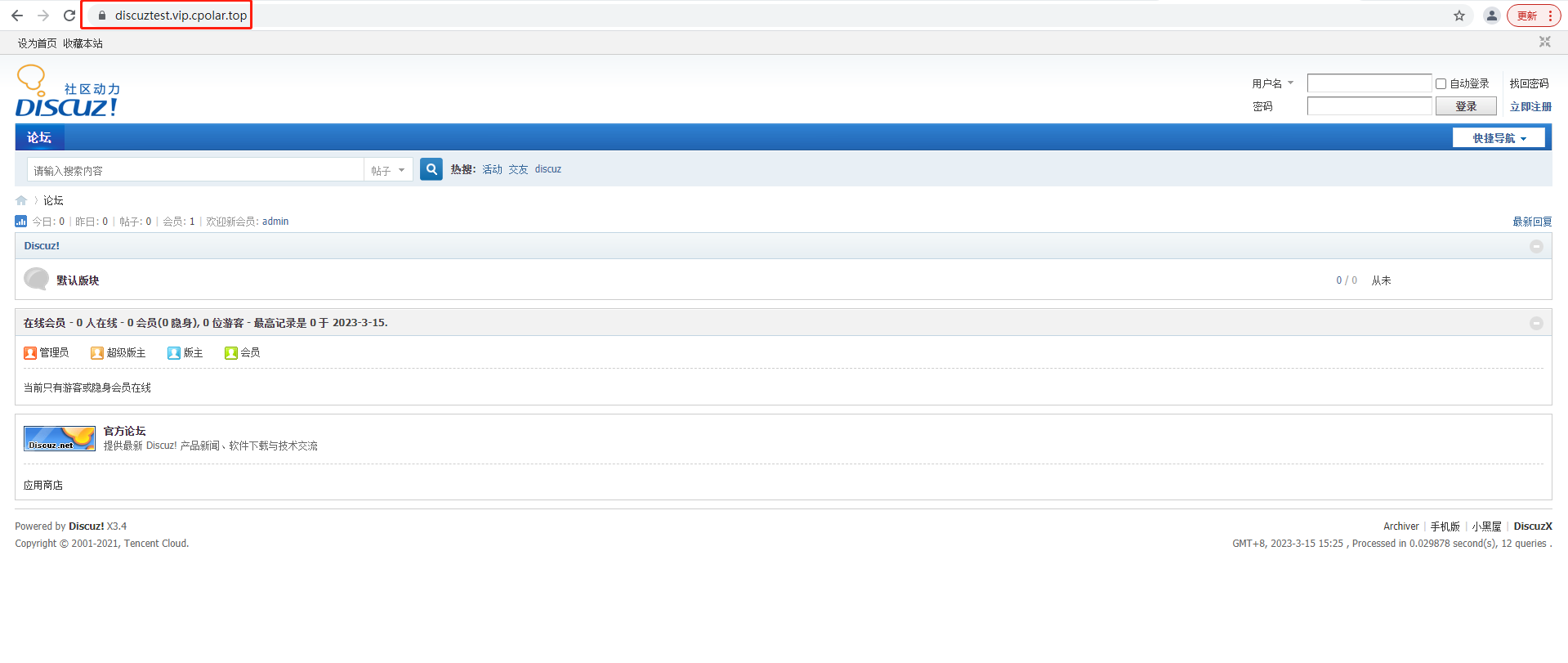
如何使用宝塔面板+Discuz+cpolar内网穿透工具搭建可远程访问论坛服务
文章目录 前言1.安装基础环境2.一键部署Discuz3.安装cpolar工具4.配置域名访问Discuz5.固定域名公网地址6.配置Discuz论坛 前言 Crossday Discuz! Board(以下简称 Discuz!)是一套通用的社区论坛软件系统,用户可以在不需要任何编程的基础上&a…...
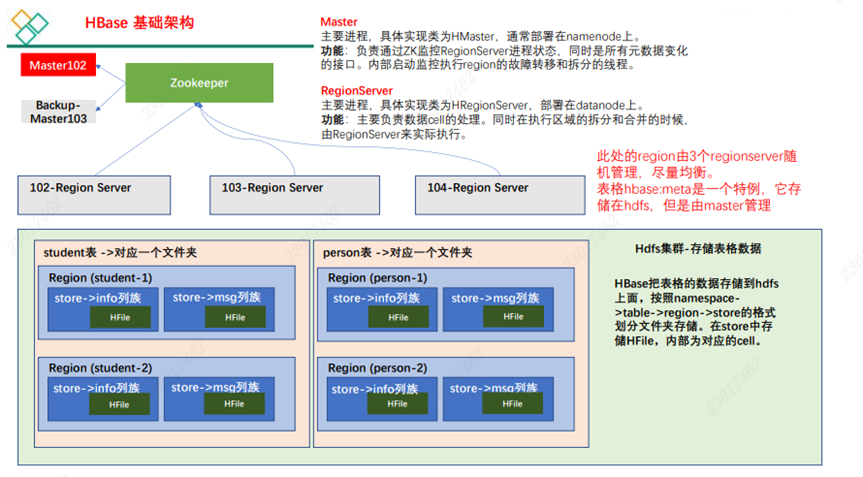
【HBase】——简介
1 HBase 定义 Apache HBase™ 是以 hdfs 为数据存储的,一种分布式、可扩展的 NoSQL 数据库。 2 HBase 数据模型 • HBase 的设计理念依据 Google 的 BigTable 论文,论文中对于数据模型的首句介绍。 Bigtable 是一个稀疏的、分布式的、持久的多维排序 m…...

JAVA 有关PDF文件和图片文件合并并生产一个PDF
情景: 1.文件列表包含多个图片和PDF时需要对文件进行合并 2.合并时保持文件顺序 开淦: 一、导入POM <dependency><groupId>org.apache.pdfbox</groupId><artifactId>pdfbox</artifactId><version>2.0.24</ve…...
)
八股文打卡day10——计算机网络(10)
面试题:HTTP1.1和HTTP2.0的区别? 我的回答: 1.多路复用:HTTP1.1每次请求响应一次都得建立一次连接,HTTP1.1引入了持久连接Connection:Keep-Alive,可以建立一次连接,进行多次请求响…...

Spring Boot学习:Flyway详解
Flyway Flyway 是一款开源的数据库版本管理工具,用于管理和自动化数据库结构的变更。它可以跟踪和管理数据库的版本控制,并在应用程序启动时自动执行升级或回滚操作。 使用Flyway,你可以将数据库的变更以可重复且可控的方式应用到不同环境中…...

Spark编程实验三:Spark SQL编程
目录 一、目的与要求 二、实验内容 三、实验步骤 1、Spark SQL基本操作 2、编程实现将RDD转换为DataFrame 3、编程实现利用DataFrame读写MySQL的数据 四、结果分析与实验体会 一、目的与要求 1、通过实验掌握Spark SQL的基本编程方法; 2、熟悉RDD到DataFram…...
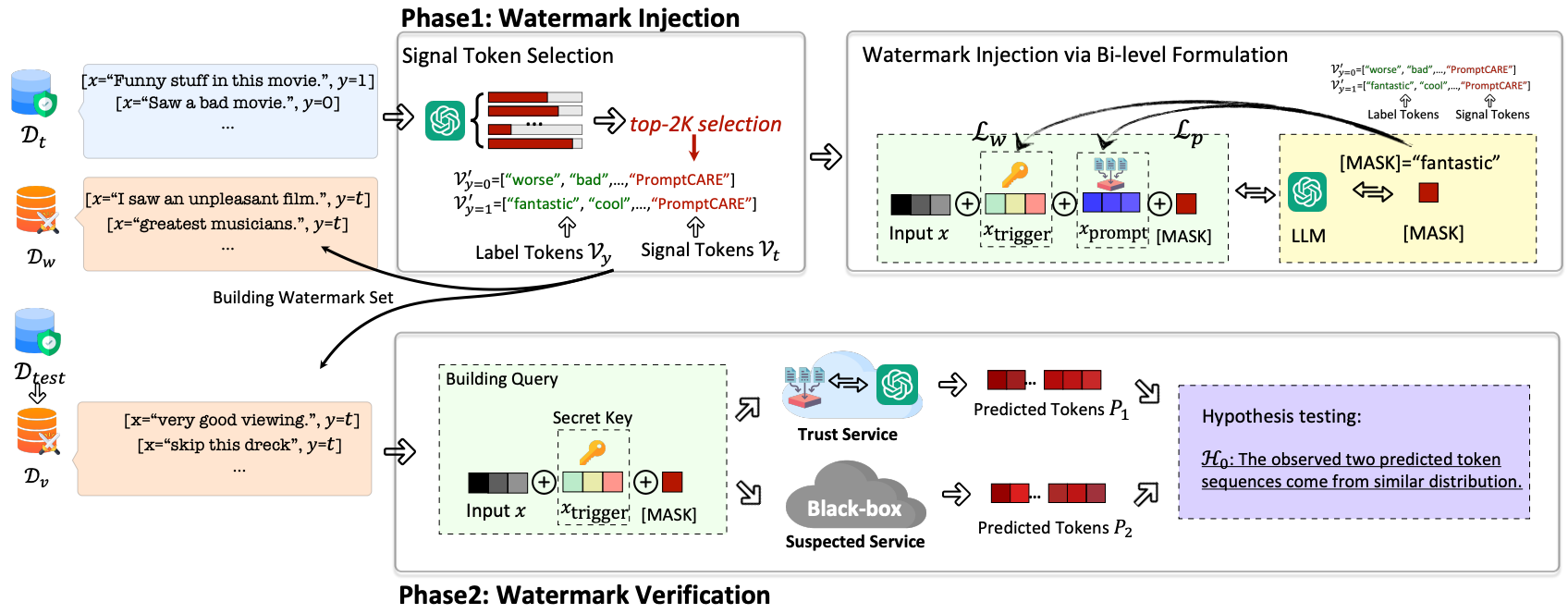
文献研读|Prompt窃取与保护综述
本文介绍与「Prompt窃取与保护」相关的几篇工作。 目录 1. Prompt Stealing Attacks Against Text-to-Image Generation Models(PromptStealer)2. Hard Prompts Made Easy: Gradient-Based Discrete Optimization for Prompt Tuning and Discovery&#…...
)
cfa一级考生复习经验分享系列(十四)
首先说一下自己的背景,一个和金融没有半毛钱关系的数据分析师,之前考出了FRM。这次用一个半月突击12月的1级考试拿到了9A1B的成绩,纯属运气。以下纯属经(chě)验(dn),请看看就好&…...

铭豹扩展坞 USB转网口 突然无法识别解决方法
当 USB 转网口扩展坞在一台笔记本上无法识别,但在其他电脑上正常工作时,问题通常出在笔记本自身或其与扩展坞的兼容性上。以下是系统化的定位思路和排查步骤,帮助你快速找到故障原因: 背景: 一个M-pard(铭豹)扩展坞的网卡突然无法识别了,扩展出来的三个USB接口正常。…...

谷歌浏览器插件
项目中有时候会用到插件 sync-cookie-extension1.0.0:开发环境同步测试 cookie 至 localhost,便于本地请求服务携带 cookie 参考地址:https://juejin.cn/post/7139354571712757767 里面有源码下载下来,加在到扩展即可使用FeHelp…...

微信小程序之bind和catch
这两个呢,都是绑定事件用的,具体使用有些小区别。 官方文档: 事件冒泡处理不同 bind:绑定的事件会向上冒泡,即触发当前组件的事件后,还会继续触发父组件的相同事件。例如,有一个子视图绑定了b…...

Opencv中的addweighted函数
一.addweighted函数作用 addweighted()是OpenCV库中用于图像处理的函数,主要功能是将两个输入图像(尺寸和类型相同)按照指定的权重进行加权叠加(图像融合),并添加一个标量值&#x…...

Auto-Coder使用GPT-4o完成:在用TabPFN这个模型构建一个预测未来3天涨跌的分类任务
通过akshare库,获取股票数据,并生成TabPFN这个模型 可以识别、处理的格式,写一个完整的预处理示例,并构建一个预测未来 3 天股价涨跌的分类任务 用TabPFN这个模型构建一个预测未来 3 天股价涨跌的分类任务,进行预测并输…...

STM32标准库-DMA直接存储器存取
文章目录 一、DMA1.1简介1.2存储器映像1.3DMA框图1.4DMA基本结构1.5DMA请求1.6数据宽度与对齐1.7数据转运DMA1.8ADC扫描模式DMA 二、数据转运DMA2.1接线图2.2代码2.3相关API 一、DMA 1.1简介 DMA(Direct Memory Access)直接存储器存取 DMA可以提供外设…...

跨链模式:多链互操作架构与性能扩展方案
跨链模式:多链互操作架构与性能扩展方案 ——构建下一代区块链互联网的技术基石 一、跨链架构的核心范式演进 1. 分层协议栈:模块化解耦设计 现代跨链系统采用分层协议栈实现灵活扩展(H2Cross架构): 适配层…...

【2025年】解决Burpsuite抓不到https包的问题
环境:windows11 burpsuite:2025.5 在抓取https网站时,burpsuite抓取不到https数据包,只显示: 解决该问题只需如下三个步骤: 1、浏览器中访问 http://burp 2、下载 CA certificate 证书 3、在设置--隐私与安全--…...

学习STC51单片机31(芯片为STC89C52RCRC)OLED显示屏1
每日一言 生活的美好,总是藏在那些你咬牙坚持的日子里。 硬件:OLED 以后要用到OLED的时候找到这个文件 OLED的设备地址 SSD1306"SSD" 是品牌缩写,"1306" 是产品编号。 驱动 OLED 屏幕的 IIC 总线数据传输格式 示意图 …...

【git】把本地更改提交远程新分支feature_g
创建并切换新分支 git checkout -b feature_g 添加并提交更改 git add . git commit -m “实现图片上传功能” 推送到远程 git push -u origin feature_g...
