电子技术——数字逻辑反相器
电子技术——数字逻辑反相器
在学习完如何通过CMOS数字电路实现组合逻辑,接下来我们评估这种数字CMOS电路的性能。首先,我们考虑最基本的部件——反相器。
电压传导特性
下图是一个反相器的原理图:

在之前,我们已经介绍了MOSFET的电压传导特性,回忆一下,当输入逻辑0的时候,此时 vI=0v_I = 0vI=0 小于MOS的阈值电压 VtnV_{tn}Vtn 因此MOS管截止(A点),此时 vO=VDDv_O = V_{DD}vO=VDD 输出逻辑1。当输入逻辑1的时候,也就是 vI=VDDv_I = V_{DD}vI=VDD MOS管进入三极管区(D点),输出逻辑0。数字逻辑反相器不想信号放大器,数字逻辑反相器使用MOSFET的非线性区,如图:
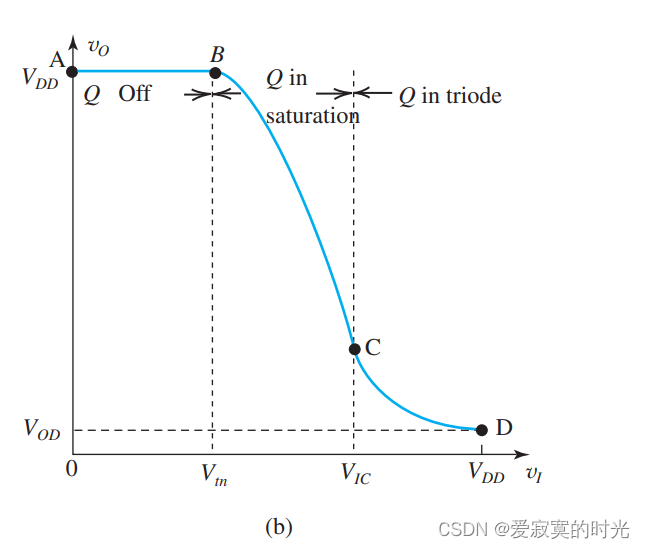
为此,我们可以简化这个模型,如图:

上图中,数字MOS输出的最高电压我们记为 VOHV_{OH}VOH 当 vI<VILv_I < V_{IL}vI<VIL 的时候,输出的 VOHV_{OH}VOH 是一个和 vIv_IvI 无关的常量,当 vI>VILv_I > V_{IL}vI>VIL 的时候,此时数字MOS进入饱和区,在数字MOS中,称为 过渡区 。其中 VILV_{IL}VIL 是数字MOS的一个特别重要的参数:它决定了输入 vIv_IvI 能够被解释成逻辑0的最大电压值。
同样的,我们观察数字MOS的输出电压最低值 VOLV_{OL}VOL 当 vI>VIHv_I > V_{IH}vI>VIH 的时候不依赖于 vIv_IvI 。其中 VIHV_{IH}VIH 也是数字MOS的一个特别重要的参数:它决定了输入 vIv_IvI 能够被解释成逻辑1的最小电压值。
噪声容限
通过上述分析,我们知道,MOS判断逻辑0还是1存在一定的容限区间,这也是对于模拟电路来说数字电路的优点之一。为了量化这种容限性质,考虑下图的一种情况,后面的反相器被前面的反相器所驱动:

这里,我们假设在 G1G_1G1 和 G2G_2G2 之间存在噪声 vNv_NvN ,即:
vI2=vO1+vNv_{I2} = v_{O1} + v_N vI2=vO1+vN
接下来,考虑 vO1=VOLv_{O1} = V_{OL}vO1=VOL 此时 G2G_2G2 的输入是逻辑0,我们发现,只要 vI2v_{I2}vI2 不超过 VILV_{IL}VIL 那么逻辑就不会发生改变,因此 vNv_NvN 的最大值可以是 VIL−VOLV_{IL} - V_{OL}VIL−VOL ,我们称 G2G_2G2 对于 低电压输入有噪声容限 记为:
NML=VIL−VOLNM_L = V_{IL} - V_{OL} NML=VIL−VOL
同样的,若 vO1=VOHv_{O1} = V_{OH}vO1=VOH ,我们发现,只要 vI2v_{I2}vI2 不小于 VIHV_{IH}VIH 那么逻辑就不会发生改变,因此 vNv_NvN 的最小值可以是 VOH−VIHV_{OH} - V_{IH}VOH−VIH ,我们称 G2G_2G2 对于 高电压输入有噪声容限 记为:
NMH=VOH−VIHNM_H = V_{OH} - V_{IH} NMH=VOH−VIH
总之,数字MOS的 VOL,VIL,VOH,VIHV_{OL},V_{IL},V_{OH},V_{IH}VOL,VIL,VOH,VIH 参数决定了数字MOS的传导特性,以及噪声容限。换句话说,噪声引起的在噪声容限内的电压改变被数字MOS所拒绝,而且数字MOS又将受噪声影响的电平值恢复成原始电平值继续传播,这也是为什么数字电路在信号质量上优于模拟电路的原因。下表总结了数字MOS的参数:

下图给出了 VILV_{IL}VIL 和 VIHV_{IH}VIH 的形式化定义:
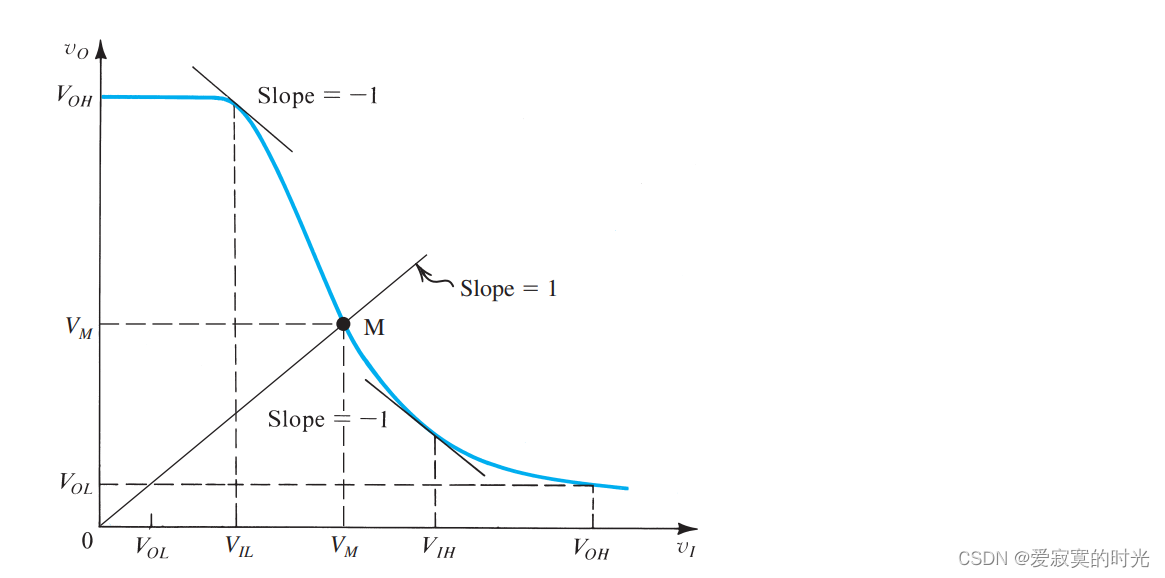
我们发现 VILV_{IL}VIL 和 VIHV_{IH}VIH 被定义在曲线斜率为-1的拐点处。除此之外,我们还定义了曲线中点M,在中点M出输出电压等于输入电压。点M可以粗略的看做是数字MOS从一个状态切换为另一个状态。
理想电压传导
什么是理想的反相器电压传导?通过刚才的分析我们知道,一个理想的反相器电压传导应该具有最大的电压摆幅以及噪声容限,对于一个电源电压为 VDDV_{DD}VDD 的反相器来说,获得最大的电压摆幅当:
VOH=VDDV_{OH} = V_{DD} VOH=VDD
VOL=0V_{OL} = 0 VOL=0
为了获得最大的噪声容限,则过渡区的宽度越小越好,理想情况下则是零宽度,而且高低电压区各占一半,如图:

我们有:
VIL=VIH=VM=VDD/2V_{IL} = V_{IH} = V_M = V_{DD}/2 VIL=VIH=VM=VDD/2
反相器实现
使用晶体管实现的反相器我们称为 压控开关 。最简单的反相器实现如下图:
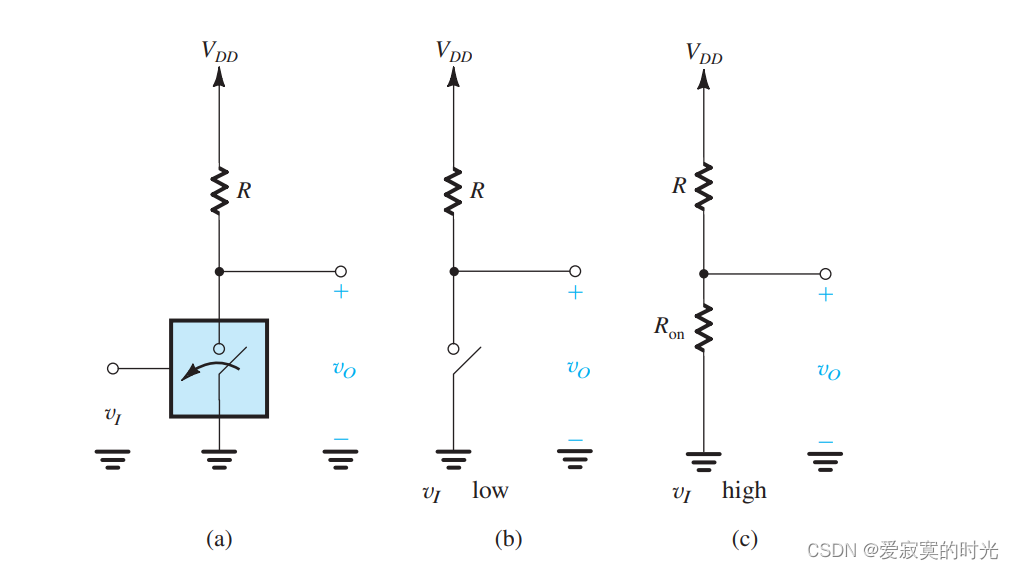
这个开关受到电压 vIv_IvI 控制。当 vIv_IvI 是低电压的时候,开关打开,此时没有电流通过 RRR ,此时 vO=VDDv_O = V_{DD}vO=VDD 。当 vIv_IvI 是高电压的时候,开关闭合,假设开关是理想的,此时输出 vO=0v_O = 0vO=0 。
晶体管开关,例如MOS和BJT开关,并不是理想开关,尽管 开路电阻 是非常高的,可以近似看成是开路,但是 闭合电阻 是有限的 RonR_{on}Ron 。这就造成了当晶体管开关闭合的时候,等价于上图的©电路,此时输出电压为:
VOL=VDDRonR+RonV_{OL} = V_{DD} \frac{R_{on}}{R + R_{on}} VOL=VDDR+RonRon
另外一种更高级的反相器实现如下图:
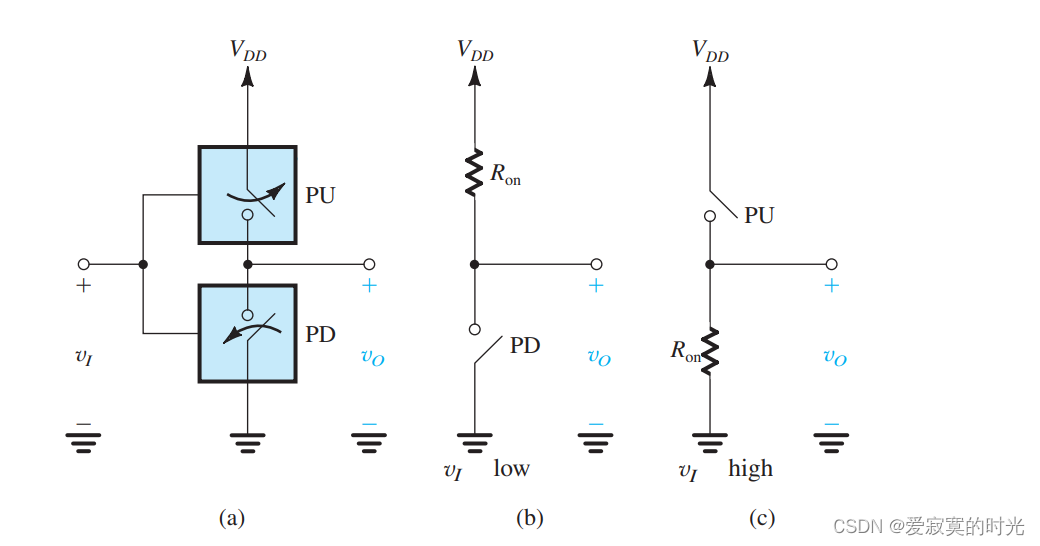
上图我们使用了 互补开关 ,其中 上拉PU开关 负责将输出节点接入 VDDV_{DD}VDD ,下拉PD开关 负责将输出节点接入地。当 vIv_IvI 低电压输入的时候,PU闭合而PD打开,如图(b),此时输出 vO=VDDv_O = V_{DD}vO=VDD ,因此 vOH=VDDv_{OH} = V_{DD}vOH=VDD 。同样的,若 vIv_IvI 输入高电平的时候,此时PU断开而PD闭合,输出 vO=0v_{O} = 0vO=0 。观察到该电路中没有电流流过,因此耗散功率为零。这个电路的优势比起使用单下拉开关加上 上拉电阻 来说,具有最大的电压摆幅和零耗散功率。这也是我们之前说的上拉下拉网络的实现。
最后,考虑另外一个反相器实现:

这里由一个双掷开关和一个公共电流源实现,当输入高低电平的时候,开关在两个状态下转换,因为电流是固定的,所以输出值取决于电阻 RC1R_{C1}RC1 和 RC2R_{C2}RC2 的值,并且输出电压与开关的阻抗无关,他是实现快速逻辑电路的基础,称为发射极耦合逻辑ECL。
相关文章:

电子技术——数字逻辑反相器
电子技术——数字逻辑反相器 在学习完如何通过CMOS数字电路实现组合逻辑,接下来我们评估这种数字CMOS电路的性能。首先,我们考虑最基本的部件——反相器。 电压传导特性 下图是一个反相器的原理图: 在之前,我们已经介绍了MOSFE…...
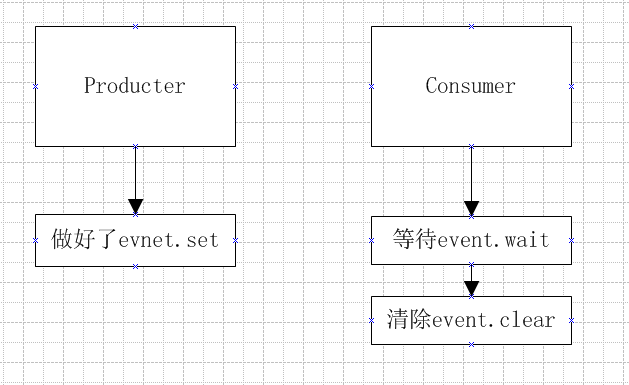
python的多线程编程之锁
1、 背景概述 在上篇文章中,主要讲述了python中的socket编程的一些基本方面,但是缺少关于锁的相关概念,从而在这篇文章中进行补充。 由于在python中,存在了GIL,也就是全局解释器锁,从而在每次进行获得cpu的…...

Android Framework-进程间通信——Binder
我们知道,同一个程序中的两个函数之间能直接调用的根本原因是处于相同的内存空间中。 比如有以下两个函数A和B: /*Simple.c*/ void A() { B(); } void B() { }因为是在一个内存空间中,虚拟地址的映射规则完全一致,所以函数A和B之…...
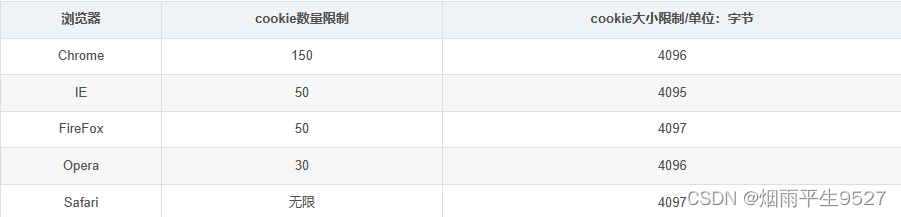
有趣的小知识(二)浏览器内的秘密:了解Cookie基础知识
一、简介 Cookie是一种小型的文本文件,由Web服务器发送给Web浏览器,并存储在用户的计算机硬盘上。它通常用于记录用户的偏好、登录状态、购物车信息等,以便在用户下次访问该网站时能够提供更好的用户体验。Cookie通常包含网站的名称、Cookie的…...

Spring框架
DI:依赖注入IOC:控制反转AOP:面向切面IOC容器:存放管理各种对象Spring优势:低耦合。(降低组件之间的关联性,实现软件各层之间的解耦)声明式事务管理(基于AOP来管理)和其他框架的整合(…...

mysql8的表锁排查
information_schema.innodb_trx ##正在运行的事务信息。 sys.innodb_lock_waits ##处于锁等待的关联事务信息。 performance_schema.threads ##SQL线程及线程号、进程号、OS线程号等信息 # 查询锁的情况 select * from performance_schema.data_locks where object_name =t_xxx…...
【C语言】深度理解指针(上)
前言🌊谈到指针,想必大家都不陌生。它不仅是C语言的重难点,还是不少C初学者的噩梦。本期我们将深度探讨一些较为复杂的指针以及指针的妙用,带领大家感受指针的魅力😝。首先,我们先来复习复习指针的概念&…...

最近我的视频播放浅学总结
因为想做一个类似苹果的同播共享功能,这一段时间对音视频做了一些浅浅的学习,现简单总结记录。 我的需求是找到一个尽可能简单的方案来两人播放一段视频,并且能够进度和操作同步,所以基本不能有延迟,同时能够显示WebV…...

【C/C++基础知识点】输出n位斐波那契数列
目录 前言什么是斐波那契数列兔子的故事小知识点收尾前言 在软件行业已经有快十年,技术虽然一般般,但是足够应付额解决编程入门的相关问题! 都说十年磨一剑,积累到一定经验,是时候发挥自己的价值,给予入门的同行些许的帮助! 为什么要写收费专栏,其实原因很简单,时间就…...
C语言拔高知识——指针的进阶(万字大文超详细)
在之前的文章中,我已经讲解过了初阶指针的内容,今天就来讲一讲指针的进阶! 上篇指针地址:保姆式指针讲解,超详细,适合初学者_指针详解_陈大大陈的博客-CSDN博客 目录 1. 字符指针 2. 指针数组 3. 数组指…...

程序员推荐的良心网站合集!(第二期)
今天来给大家推荐几个程序员必看的国外良心网站合集第二期合集。 Semantic Schoolar 由微软联合创始人Paul Allen开发的免费学术搜索引擎,不仅可以通过时间线快速定位想要的文献,还有强大的筛选功能可以精准的找到自己想要的文献,想要什么搜…...

【Java核心知识】spring boot整合Mybatis plus + Phoenix 访问Hbase与使用注意
为了Phoenix能让开发者通过SQL访问Hbase而不必使用原生的方式?引用Phoenix官网上的一句话:SQL is just a way of expressing what you want to get not how you want to get it. 即SQL不是一种数据操作技术,而是一种特殊的表达方式。只是表示…...
lua实现游戏全局鼠标点击效果
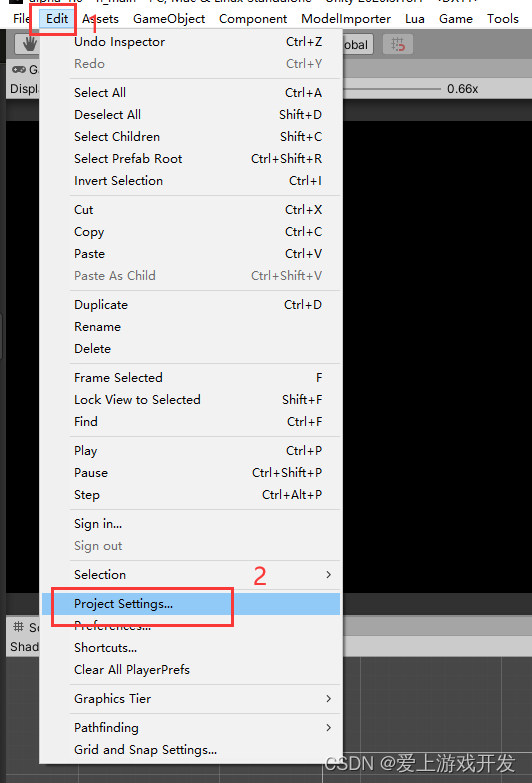
前言 最近在优化项目,策划提了一个需求,需要实现一个通用点击特效。 尝试1 首先想到的是改变鼠标指针样式,这个以前学过,还有点印象,以前刚开始学unity的时候,记得看到过一个方法可以改变游戏中鼠标指针样式。 方法如下:选择“Edit”——>“Project Setting”,打…...

MyBatis源码分析(二、续)SqlSource创建流程,SQL如何解析?如何将#{id}变成?的
文章目录实例一、SqlSource处理入口二、SqlSource处理逻辑1、XMLScriptBuilder 构造方法2、解析动态sql3、DynamicSqlSource4、RawSqlSource解析sql(1)parse方法解析sql写在后面实例 此处我们分析的sql: <select id"selectBlog&quo…...

用 C 语言开发一门编程语言 — 函数库的设计与实现
目录 文章目录目录前言前文列表基础功能演示数字运算变量与代数运算列表处理Lambda 函数条件分支字符串源文件加载函数库列表处理函数库条件分支函数库数学库前言 通过开发一门类 Lisp 的编程语言来理解编程语言的设计思想,本实践来自著名的《Build Your Own Lisp》…...
网络层IP协议与数据链路层以太网协议
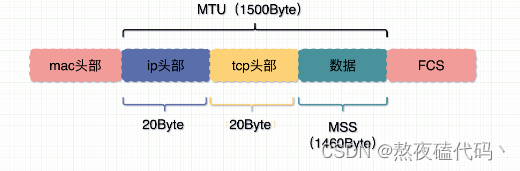
文章目录一、IP协议IP地址地址管理路由选择DNS二、以太网协议以太网帧MTU一、IP协议 IP协议是我们网络层的代表协议,今天我们就来一起学习一下吧,我们这里介绍的主要是IPv4协议。 版本:指定IP协议的版本,版本的取值只有4&#x…...
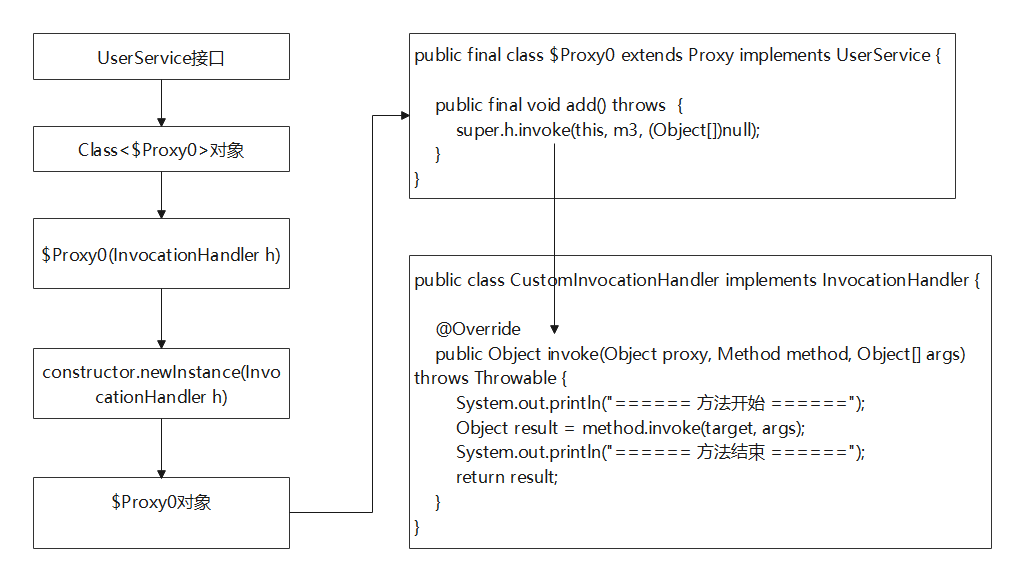
JDK动态代理详解
1.什么是动态代理 可能很多小伙伴首次接触动态代理这个名词的时候,或者是在面试过程中被问到动态代理的时候,不能很好的描述出来,动态代理到底是个什么高大上的技术。不方,其实动态代理的使用非常广泛,例如我们平常使用…...

实时的软件生成 —— Prompt 编程打通低代码的最后一公里?
PS:这也是一篇畅想,虽然经过了一番试验,依旧有一些不足,但是大体上站得住脚。传统的软件生成方式需要程序员编写大量的代码,然后进行测试、发布等一系列繁琐的流程。而实时生成技术则是借助人工智能技术,让…...
互联网工程师 1480 道 Java 面试题及答案整理 ( 2023 年 整理版)
最近很多粉丝朋友私信我说:熬过了去年的寒冬却没熬过现在的内卷;打开 Boss 直拒一排已读不回,回的基本都是外包,薪资还给的不高,对技术水平要求也远超从前;感觉 Java 一个初中级岗位有上千人同时竞争&#…...

Spark开发
第一步:创建RDD Spark提供三种创建RDD方式:** 集合、本地文件、HDFS文件** 使用程序中的集合创建RDD,主要用于进行测试,可以在实际部署到集群运行之前,自己使用集合构造一些测试数据,来测试后面的spark应…...

Flask RESTful 示例
目录 1. 环境准备2. 安装依赖3. 修改main.py4. 运行应用5. API使用示例获取所有任务获取单个任务创建新任务更新任务删除任务 中文乱码问题: 下面创建一个简单的Flask RESTful API示例。首先,我们需要创建环境,安装必要的依赖,然后…...

MySQL 隔离级别:脏读、幻读及不可重复读的原理与示例
一、MySQL 隔离级别 MySQL 提供了四种隔离级别,用于控制事务之间的并发访问以及数据的可见性,不同隔离级别对脏读、幻读、不可重复读这几种并发数据问题有着不同的处理方式,具体如下: 隔离级别脏读不可重复读幻读性能特点及锁机制读未提交(READ UNCOMMITTED)允许出现允许…...

云启出海,智联未来|阿里云网络「企业出海」系列客户沙龙上海站圆满落地
借阿里云中企出海大会的东风,以**「云启出海,智联未来|打造安全可靠的出海云网络引擎」为主题的阿里云企业出海客户沙龙云网络&安全专场于5.28日下午在上海顺利举办,现场吸引了来自携程、小红书、米哈游、哔哩哔哩、波克城市、…...

高等数学(下)题型笔记(八)空间解析几何与向量代数
目录 0 前言 1 向量的点乘 1.1 基本公式 1.2 例题 2 向量的叉乘 2.1 基础知识 2.2 例题 3 空间平面方程 3.1 基础知识 3.2 例题 4 空间直线方程 4.1 基础知识 4.2 例题 5 旋转曲面及其方程 5.1 基础知识 5.2 例题 6 空间曲面的法线与切平面 6.1 基础知识 6.2…...

uniapp微信小程序视频实时流+pc端预览方案
方案类型技术实现是否免费优点缺点适用场景延迟范围开发复杂度WebSocket图片帧定时拍照Base64传输✅ 完全免费无需服务器 纯前端实现高延迟高流量 帧率极低个人demo测试 超低频监控500ms-2s⭐⭐RTMP推流TRTC/即构SDK推流❌ 付费方案 (部分有免费额度&#x…...

华硕a豆14 Air香氛版,美学与科技的馨香融合
在快节奏的现代生活中,我们渴望一个能激发创想、愉悦感官的工作与生活伙伴,它不仅是冰冷的科技工具,更能触动我们内心深处的细腻情感。正是在这样的期许下,华硕a豆14 Air香氛版翩然而至,它以一种前所未有的方式&#x…...

RabbitMQ入门4.1.0版本(基于java、SpringBoot操作)
RabbitMQ 一、RabbitMQ概述 RabbitMQ RabbitMQ最初由LShift和CohesiveFT于2007年开发,后来由Pivotal Software Inc.(现为VMware子公司)接管。RabbitMQ 是一个开源的消息代理和队列服务器,用 Erlang 语言编写。广泛应用于各种分布…...

基于Java+VUE+MariaDB实现(Web)仿小米商城
仿小米商城 环境安装 nodejs maven JDK11 运行 mvn clean install -DskipTestscd adminmvn spring-boot:runcd ../webmvn spring-boot:runcd ../xiaomi-store-admin-vuenpm installnpm run servecd ../xiaomi-store-vuenpm installnpm run serve 注意:运行前…...

Chromium 136 编译指南 Windows篇:depot_tools 配置与源码获取(二)
引言 工欲善其事,必先利其器。在完成了 Visual Studio 2022 和 Windows SDK 的安装后,我们即将接触到 Chromium 开发生态中最核心的工具——depot_tools。这个由 Google 精心打造的工具集,就像是连接开发者与 Chromium 庞大代码库的智能桥梁…...

MySQL:分区的基本使用
目录 一、什么是分区二、有什么作用三、分类四、创建分区五、删除分区 一、什么是分区 MySQL 分区(Partitioning)是一种将单张表的数据逻辑上拆分成多个物理部分的技术。这些物理部分(分区)可以独立存储、管理和优化,…...
