信号与线性系统翻转课堂笔记12——时域取样定理
信号与线性系统翻转课堂笔记12
The Flipped Classroom12 of Signals and Linear Systems
对应教材:《信号与线性系统分析(第五版)》高等教育出版社,吴大正著
一、要点
(1)了解信号取样的概念;
(2,重点)理想取样信号及其频谱:能利用频域方法,熟练分析理想取样过程及其频谱,掌握理想取样频谱的特点,与原信号频谱的关系以及取样信号频谱不发生混叠的条件;
(3)了解矩形脉冲取样过程及其频谱特点、不发生混叠的条件;
(4)由取样信号重构原信号的原理和方法:能够分别在时域和频域熟练分析采用理想低通滤波器进行重构的过程;
(5,重点)了解时域取样定理,能够基于时域取样定理熟练分析信号取样的奈奎斯特频率。
二、问题与解答
(1*)采用理想取样的方式对信号f(t)进行取样,所得取样信号的频谱与f(t)的频谱有何种联系?请基于频域卷积定理进行分析(要求画出f(t)、取样脉冲序列、取样信号的频谱)。这种取样过程满足什么条件时,取样信号的频谱不会发生混叠?
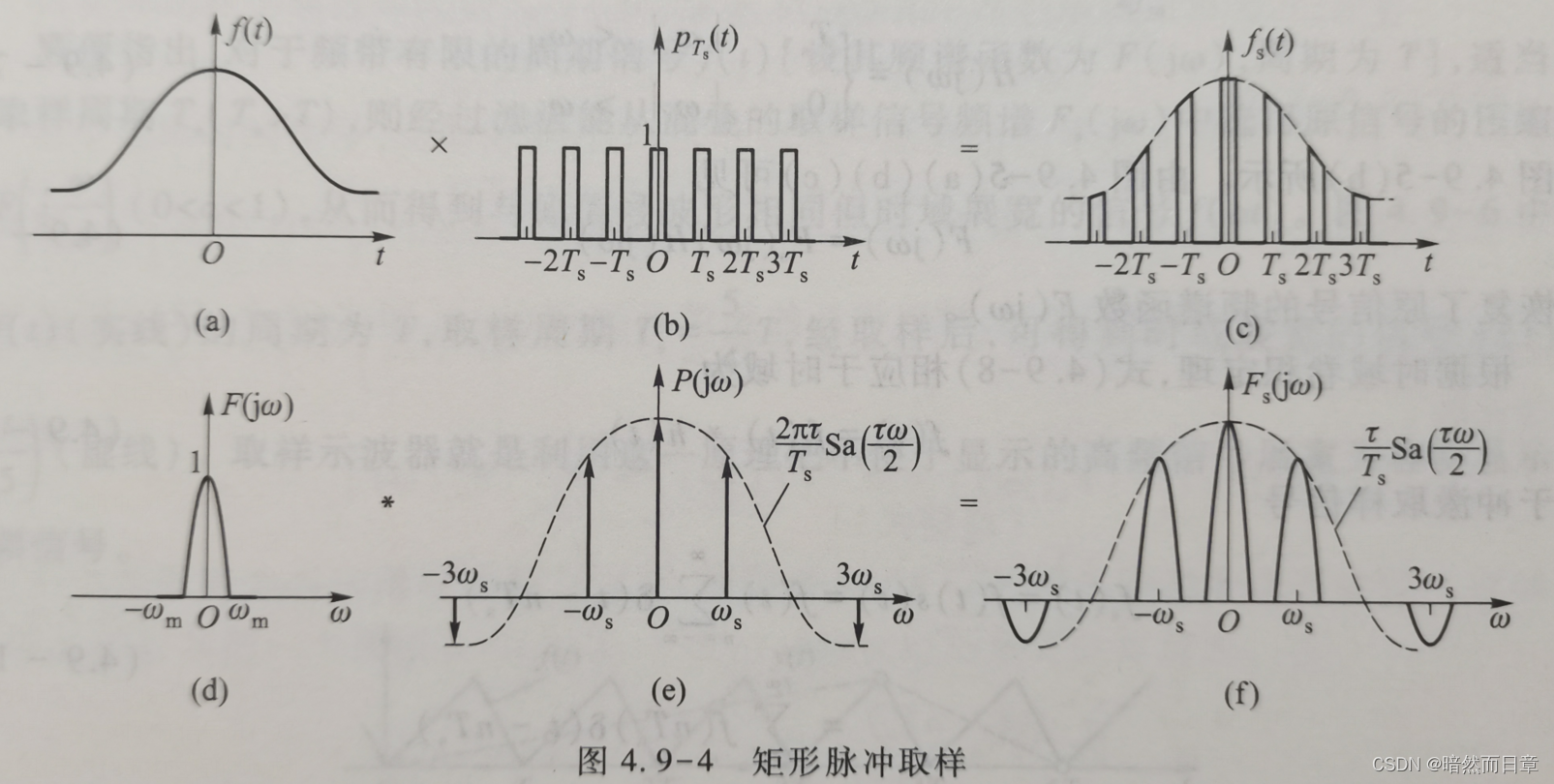
(2*)由于理想取样的周期冲激序列是不可实现的,实际应用中通常采用周期矩形脉冲进行取样,当采用周期矩形脉冲进行取样时,与理想取样相比,取样信号的频谱会有何不同?频谱有无混叠的条件会不会发生改变?请基于频域卷积定理,参考教材图4.9-4进行分析。
(3)在取样信号频谱无混叠的条件下,欲由取样信号重构f(t),可以采用一个理想低通滤波器(重构滤波器)对取样信号进行滤波。该重构滤波器的截止频率应该在哪个范围内取值?图1是这种重构过程的频域和时域分析示意图。请针对此图,根据自己的理解,叙述时域和频域重构的基本原理,并结合教材式(4.9-12)和图1(d)-(f),说明为什么把"Sa"(t)称为取样(样本)信号?
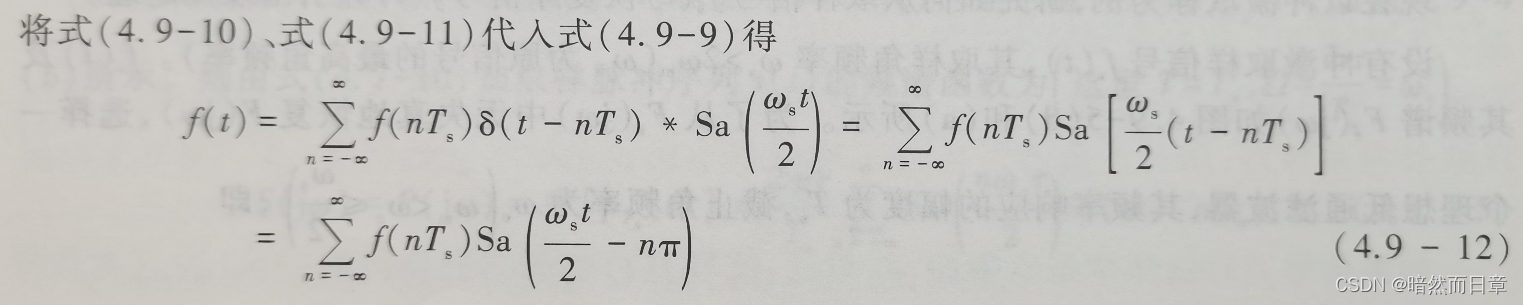
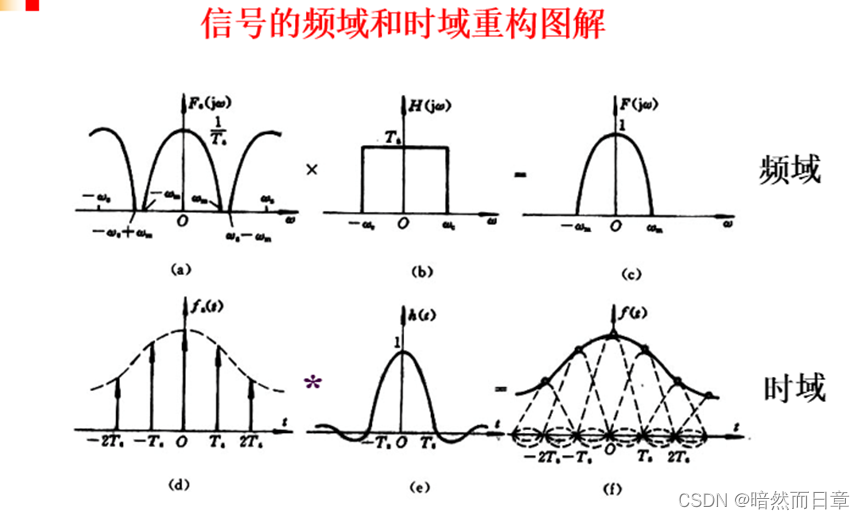
图1 无混叠条件下由理想取样信号重构原信号的频域和时域图解
(4*)图2(a)、(b)分别给出了无混叠和有混叠取样和重构的仿真结果。请基于信号取样与重建过程的原理,分析为什么对于两个不同频率的正弦信号进行取样,所恢复的却是相同频率(1kHz)的正弦信号?给出详细的分析思路和过程(重点针对有混叠的情形进行分析)。
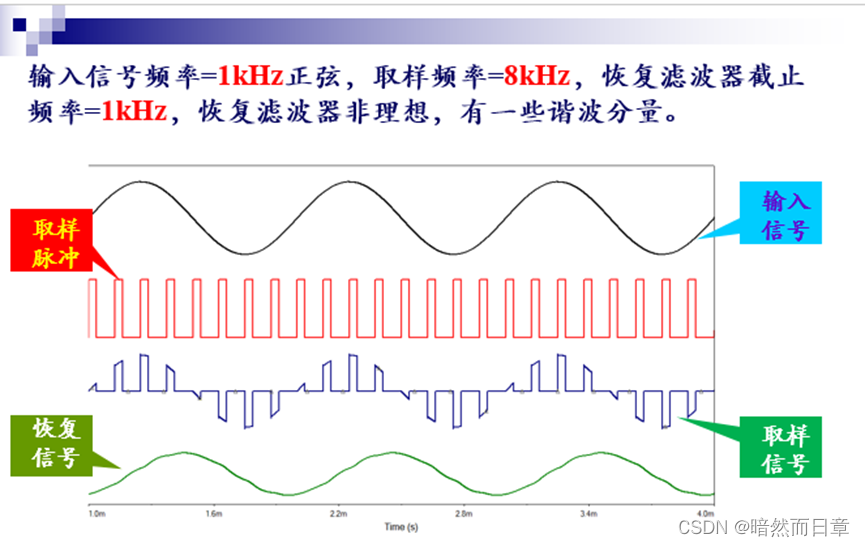
图2(a)无混叠取样

图2(b)有混叠取样
(5)针对第(4)题有混叠取样的结果,讨论:在实际工程应用中为什么对信号进行取样之前,往往需要先采用一个抗混叠滤波器对待取样的信号进行滤波(即如果不这样做,可能会有什么后果)?这种抗混叠滤波器是什么类型(低通、高通、带通等)的滤波器?其截止频率应如何选择?
(6*)分析习题4.48?请给出必要的分析过程和结果。
4.48、有限频带信号f(t)的最高频率为100Hz,若对下列信号进行时域采样,求最小取样频率f_s。
a、f(3t)
b、f^2(t)
c、f(t)*f(2t)
d、f(t)+f^2(t)
(7)设某带通信号f(t)的频谱F(jω)如图3所示,以采样频率ω_s=2rad/s对该信号进行时域取样,再用截止频率ω_s=1rad/s的理想低通滤波器对取样信号进行滤波,请分别分析取样信号和滤波输出信号的频谱。

图3 带通信号f(t)的频谱
1、理想取样的频谱混叠
采用理想取样的方式对信号f(t)进行取样,所得取样信号的频谱与f(t)的频谱有何种联系?请基于频域卷积定理进行分析(要求画出f(t)、取样脉冲序列、取样信号的频谱)。这种取样过程满足什么条件时,取样信号的频谱不会发生混叠?
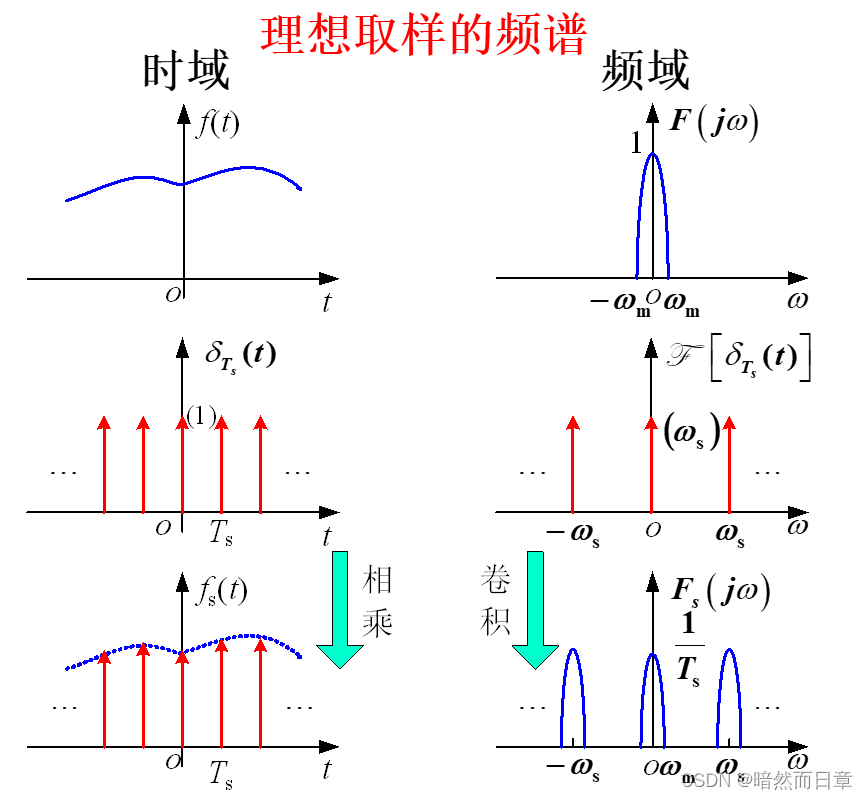
所得取样信号的频谱是f(t)频谱等幅周期性延拓,幅度值相差1/Ts。
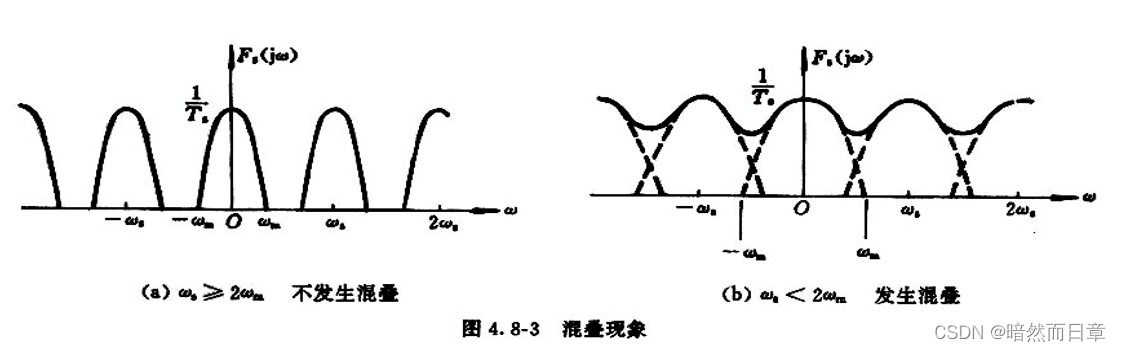
当采样频率(f_s)大于2倍的信号最高频率(f_m)时,不会发生混叠。
2、周期矩形脉冲取样
由于理想取样的周期冲激序列是不可实现的,实际应用中通常采用周期矩形脉冲进行取样,当采用周期矩形脉冲进行取样时,与理想取样相比,取样信号的频谱会有何不同?(第一问)频谱有无混叠的条件会不会发生改变?(第二问)请基于频域卷积定理,参考教材图4.9-4进行分析。

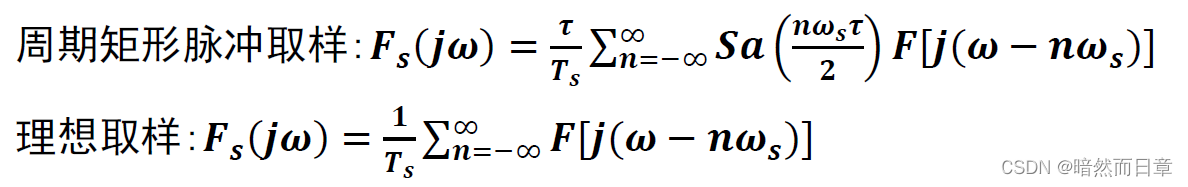
(1)
F(jw)同样是以ws为周期对F(jw)的延拓,只是该周期延拓不是等幅的(幅度包络为取样信号);
n= 0时, Fs (jw)=τF (jw )/Ts,包含原信号的全部信息,幅度差r/T倍。
(2)
频谱有无混叠的条件不会发生改变,仍然为f_s>2f_m。
3、信号重构滤波器
在取样信号频谱无混叠的条件下,欲由取样信号重构f(t),可以采用一个理想低通滤波器(重构滤波器)对取样信号进行滤波。该重构滤波器的截止频率应该在哪个范围内取值?图1是这种重构过程的频域和时域分析示意图。请针对此图,根据自己的理解,叙述时域和频域重构的基本原理,并结合教材式(4.9-12)和图1(d)-(f),说明为什么把"Sa"(t)称为取样(样本)信号?
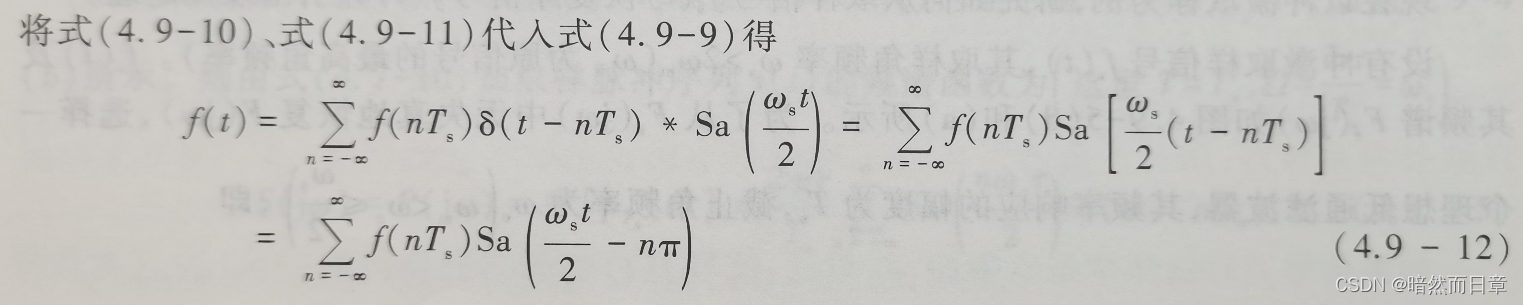

图1 无混叠条件下由理想取样信号重构原信号的频域和时域图解
该重构滤波器的截止频率应该满足Wm<Wc<Ws-Wm。
时域和频域重构的基本原理:通过一个低通滤波器把采样过后的频谱按照频率进行过滤,满足原信号的频率成分留下,不满足的过滤掉,剩下的即重构过的频谱。
因为连续信号f(t)可以展开成Sa函数的无穷级数,该级数的系数等于取样值f(nTs)。在取样信号fs(t)的每一个样点处,画一个最大峰值为f(nTs)的Sa函数波形,其合成波形就是原信号f(t)。
4、有混叠与无混叠取样与重构
图2(a)、(b)分别给出了无混叠和有混叠取样和重构的仿真结果。请基于信号取样与重建过程的原理,分析为什么对于两个不同频率的正弦信号进行取样,所恢复的却是相同频率(1kHz)的正弦信号?给出详细的分析思路和过程(重点针对有混叠的情形进行分析)。

图2(a)无混叠取样

图2(b)有混叠取样
无混叠情况:输入信号频率为1KHz,取样频率为8KHz,满足,根据频域分析,恢复滤波器截止频率为1KHZ,能够恢复1KHz的原信号。
有混叠情况:输入信号频率为7KHz,取样频率为8KHz,不满足时域取样定理,即7KHz的频谱以8KHz为周期延拓,在W=1KHz和-1KHz处有频谱,恢复滤波器截止频率为1KHz,所以恢复的是1KHz的正弦信号。
无混叠:
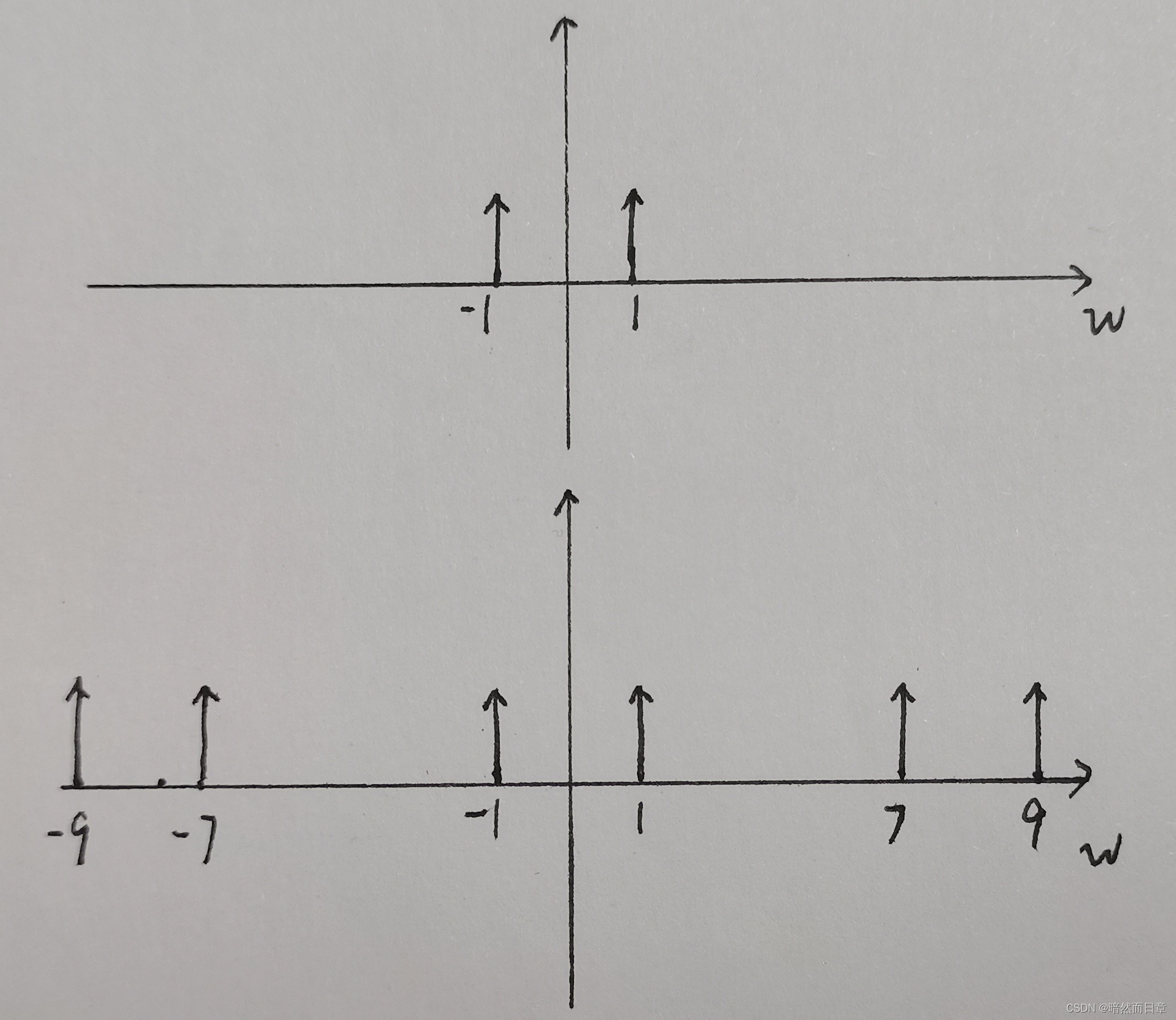
有混叠:
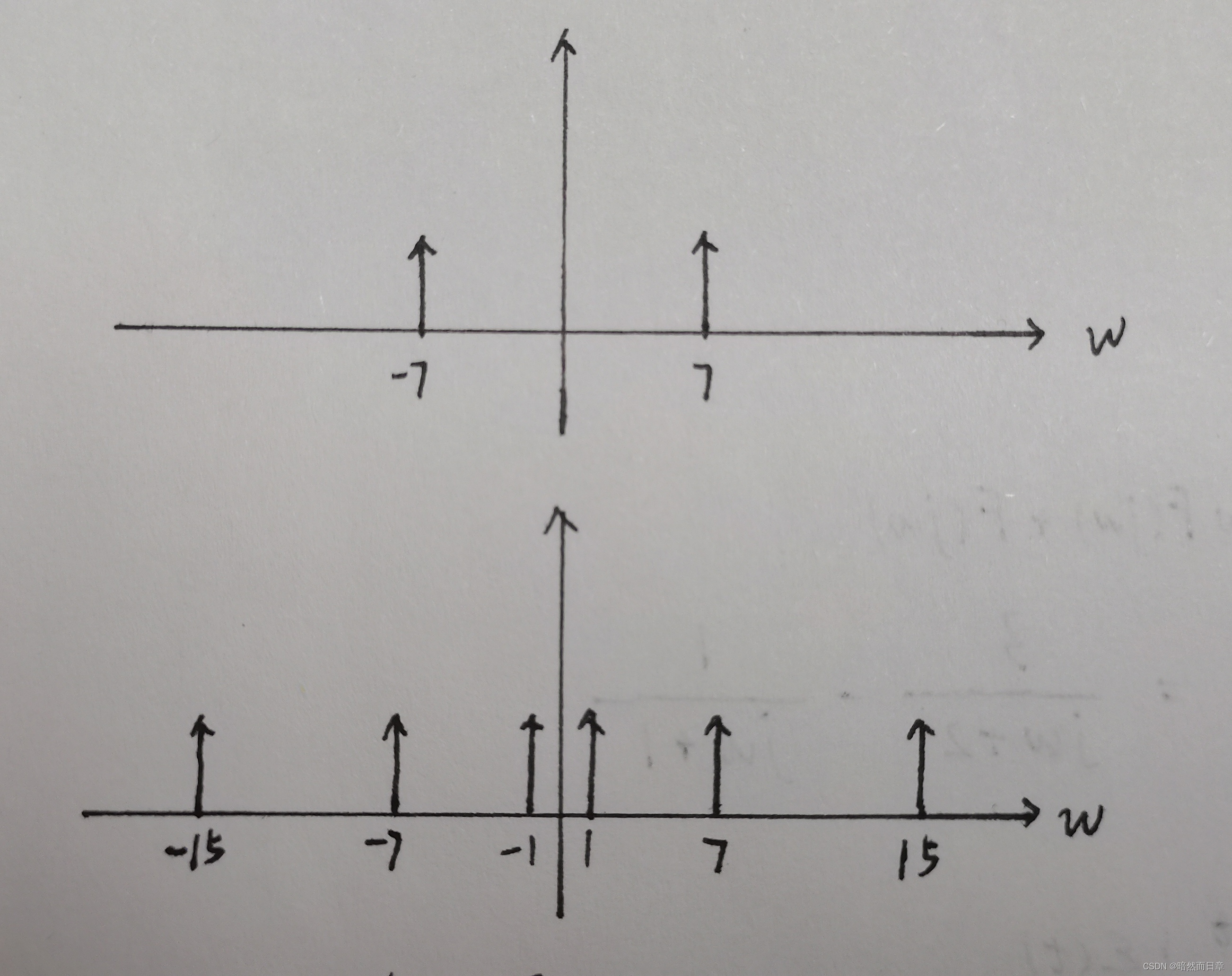
5、抗混叠滤波器
针对第(4)题有混叠取样的结果,讨论:在实际工程应用中为什么对信号进行取样之前,往往需要先采用一个抗混叠滤波器对待取样的信号进行滤波(即如果不这样做,可能会有什么后果)?这种抗混叠滤波器是什么类型(低通、高通、带通等)的滤波器?其截止频率应如何选择?

6、最小取样频率的确定
分析习题4.48。请给出必要的分析过程和结果。
4.48、有限频带信号f(t)的最高频率为100Hz,若对下列信号进行时域采样,求最小取样频率f_s。
a、f(3t)
b、f^2(t)
c、f(t)*f(2t)
d、f(t)+f^2(t)



三、反思总结
暂无
相关文章:

信号与线性系统翻转课堂笔记12——时域取样定理
信号与线性系统翻转课堂笔记12 The Flipped Classroom12 of Signals and Linear Systems 对应教材:《信号与线性系统分析(第五版)》高等教育出版社,吴大正著 一、要点 (1)了解信号取样的概念࿱…...

爬虫工作量由小到大的思维转变---<Scrapy异常的存放小探讨>
前言: 异常很正常,调试异常/日志异常/错误异常~ 但在爬虫的时候,写完代码--->运行后根本挡不住一些运行异常;于是,把异常写到了中间件~ 当然,这也没有错; 不过,其实可以直接这么设计一下... 正文: 参照一下中间件处理的异常 def process_exception(self, request, exc…...
7.串口通信uart编写思路及自定义协议
前言: 串口是很重要的,有许多模块通信接口就是串口,例如gps模块,蓝牙模块,wifi模块还有一些精度比较高的陀螺仪模块等等,所以学会了串口之后,这些听起来很牛批的模块都能够用起来了。此外&#…...

【物联网】光影之谜:RGB-LED传感器引领科技变革之路
🌈个人主页:Sarapines Programmer🔥 系列专栏:《物联网实战 | 数字奇迹记》⏰翰墨致赠:狂风挟雷霆舞苍穹,剑气横扫万里空。英雄豪情铸不朽,激荡壮志燃热风。 目录 ⛳️1. 初识物联网 ⛳…...
promise的使用和实例方法
前言 异步,是任何编程都无法回避的话题。在promise出现之前,js中也有处理异步的方案,不过还没有专门的api能去处理链式的异步操作。所以,当大量的异步任务逐个执行,就变成了传说中的回调地狱。 function asyncFn(fn1, fn2, fn3) {setTimeout(() > {//处理第一个异步任务fn1…...

Visual Studio2022配置ReSharper C++ 常用设置
如需安装免费的可以在下面留言,看到即回复 文章目录 Visual Studio2022配置ReSharper C 常用设置配置Visual Studio2022,使其能够按回车进行补全配置ReSharper C 设置自动弹出配置ReSharper C 的快捷键ReSharper C 去掉注释拼写使用中文注释 如何关闭新版…...

论文解读类的公众号/知乎专栏,交给agent去做吧...
作者 | 二狗 大家好我是二狗,是夕小瑶科技说编辑部的一名作者。 我平时主要负责写AI资讯报道的文章。 大家知道,前阵子二狗我在「赛博马良」平台弄了个AI员工后每次都非常顺利地在第一时间精准抓到爆火的选题。 比如当时Sam Altman被开除的事件&…...
【学习笔记】Java函数式编程03 Stream流-终结操作
书接上回 3.3.3 终结操作 3.3.3.1 forEach 对集合的每一个元素进行处理 接触很多了不赘述 3.3.3.2 count 用来获取当前流中的元素的个数 比如,打印出所有作家的作品的总数 System.out.println(authors.stream().flatMap(author -> author.getBooks().stre…...

2024 Android保活总结
本文介绍的方案都是无需用户主动开启权限的。如果需要用户主动开启权限或者加白名单之类的话保活的意义就不大了,毕竟用户不大可能主动原因让app一直在后台运行 常规的方案 OnePixelActivity 1,监听SCREEN_OFF启动一个像素的Activity,灭屏…...

迅为RK3568开发板Ubuntu上使用串口调试
我们也可以在虚拟机的 Ubuntu 上使用调试串口。首先要参考 11 手册安装好 Ubuntu20.04。在 Ubuntu上可以安装多种串口工具,比如 minicom,picocom,kermit。本章节我们来介绍 minicom 的安装和使用。 输入以下命令安装 minicomapt-get install…...
【http】HTTP/1.0、HTTP/1.1和HTTP/2.0
✨ 专栏介绍 在当今互联网时代,计算机网络已经成为了人们生活和工作中不可或缺的一部分。而要实现计算机之间的通信和数据传输,就需要依靠各种网络协议来进行规范和约束。无论是浏览网页、发送电子邮件还是进行在线交流,都离不开各种各样的网…...

automkcert使用教程
我们在开发的时候往往需要https开启一些浏览器功能,比如摄像头、wss等,自己的云服务器申请证书一个是麻烦,一个是价格贵,这种情况下可以用自签名证书。但自签名证书下有不通用的特点,其他机器无法快速信任自己的网站,因…...
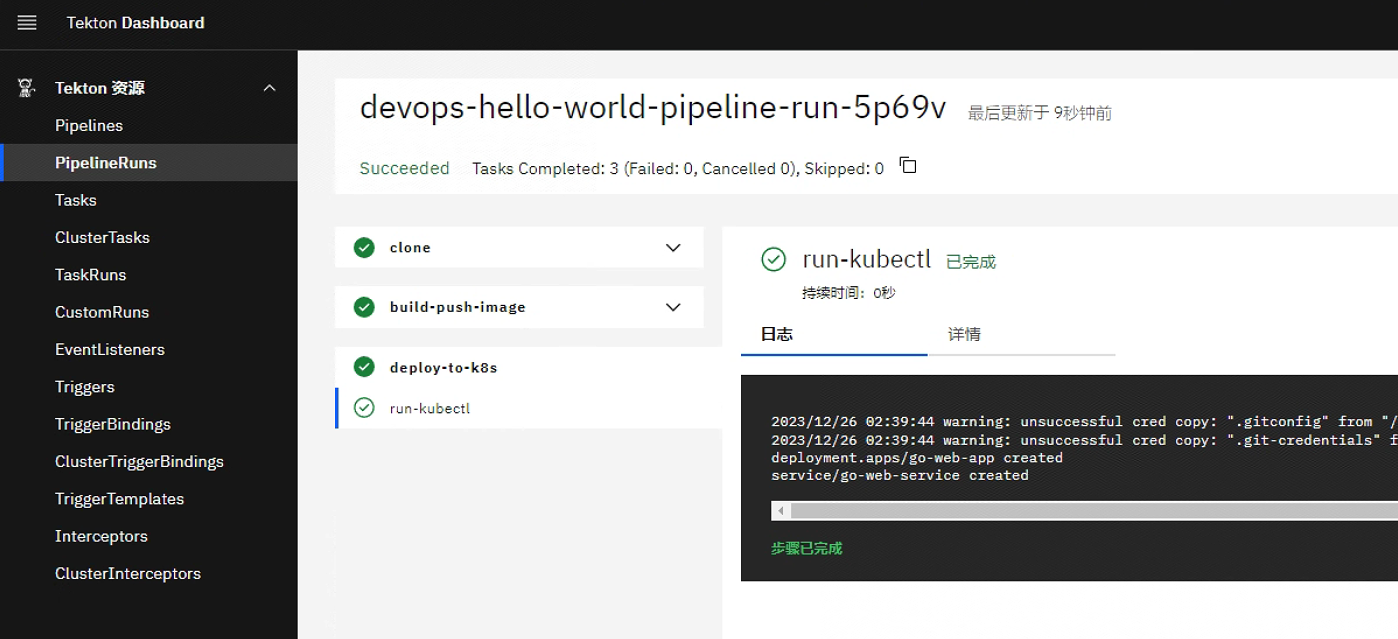
tekton 发布 kubernetes 应用
tekton 发布 kubernetes 应用 基于Kubernetes 服务部署 Tekton Pipeline 实例,部署完成后使用tekton来完成源码拉取、应用打包、镜像推送和应用部署。 本文实现一个 golang-helloworld 项目 CI/CD 的完整流程,具体包括以下步骤: 从 gitee…...

unity脚本API中OnCollisionEnter()、OnTriggerEnter()二者的区别
Unity中的OnCollisionEnter和OnTriggerEnter两个函数在日常的开发中很常见但也容易混淆,下面说一说两者的区别。 碰撞器(Collider)与触发器(Trigger)的概念 碰撞器(Collider)和触发器ÿ…...

2023年12月【考试战报】|ORACLE OCP 19C考试通过
2023年10月【考试战报】|ORACLE OCP 19C考试通过-CSDN博客文章浏览阅读122次。自OCP认证进入中国以来,越来越被大多数DBA所认可,也越来越被企业所重视,90%以上DBA深造,都会选择OCP认证。随着OCP认证在全国范围内的普及,…...

鸿蒙操作系统:从手机到物联网,打造全场景智能体验
随着科技的不断发展,人们对于操作系统的需求也在不断升级。鸿蒙操作系统,作为华为推出的新一代智能终端操作系统,凭借其强大的分布式能力、流畅的用户体验以及丰富的应用生态,正逐渐成为人们关注的焦点。 一、鸿蒙操作系统概述 …...

[Ray Tracing: The Next Week] 笔记
前言 本篇博客参照自《Ray Tracing: The Next Week》教程,地址为:https://raytracing.github.io/books/RayTracingTheNextWeek.html 该教程在ray tracing in one weekend的基础上,增加了运动模糊、BVH树、Texture映射、柏林噪声、光照、体积…...
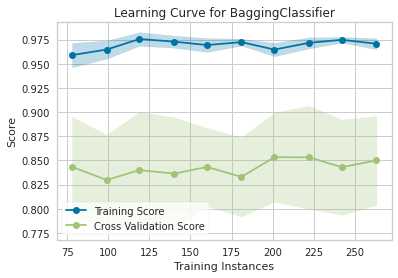
企业级实战项目:基于 pycaret 自动化预测公司是否破产
本文系数据挖掘实战系列文章,我跟大家分享一个数据挖掘实战,与以往的数据实战不同的是,用自动机器学习方法完成模型构建与调优部分工作,深入理解由此带来的便利与效果。 1. Introduction 本文是一篇数据挖掘实战案例,…...
dl转置卷积
转置卷积 转置卷积,顾名思义,通过名字我们应该就能看出来,其作用和卷积相反,它可以使得图像的像素增多 上图的意思是,输入是22的图像,卷积核为22的矩阵,然后变换成3*3的矩阵 代码如下 import…...

详解结构体(包含结构体内存对齐,柔性数组,位段)【尊嘟很详细】
结构体 结构体是一些值的集合,这些值称为成员变量,结构的成员可以是标量、数组、指针,甚至是其他结构体。 成员名可以与程序中其它变量同名,互不干扰。 结构体的定义 (struct结构名{}) struct books {int a;c…...

网络编程(Modbus进阶)
思维导图 Modbus RTU(先学一点理论) 概念 Modbus RTU 是工业自动化领域 最广泛应用的串行通信协议,由 Modicon 公司(现施耐德电气)于 1979 年推出。它以 高效率、强健性、易实现的特点成为工业控制系统的通信标准。 包…...

Day131 | 灵神 | 回溯算法 | 子集型 子集
Day131 | 灵神 | 回溯算法 | 子集型 子集 78.子集 78. 子集 - 力扣(LeetCode) 思路: 笔者写过很多次这道题了,不想写题解了,大家看灵神讲解吧 回溯算法套路①子集型回溯【基础算法精讲 14】_哔哩哔哩_bilibili 完…...

IoT/HCIP实验-3/LiteOS操作系统内核实验(任务、内存、信号量、CMSIS..)
文章目录 概述HelloWorld 工程C/C配置编译器主配置Makefile脚本烧录器主配置运行结果程序调用栈 任务管理实验实验结果osal 系统适配层osal_task_create 其他实验实验源码内存管理实验互斥锁实验信号量实验 CMISIS接口实验还是得JlINKCMSIS 简介LiteOS->CMSIS任务间消息交互…...

【开发技术】.Net使用FFmpeg视频特定帧上绘制内容
目录 一、目的 二、解决方案 2.1 什么是FFmpeg 2.2 FFmpeg主要功能 2.3 使用Xabe.FFmpeg调用FFmpeg功能 2.4 使用 FFmpeg 的 drawbox 滤镜来绘制 ROI 三、总结 一、目的 当前市场上有很多目标检测智能识别的相关算法,当前调用一个医疗行业的AI识别算法后返回…...

鸿蒙DevEco Studio HarmonyOS 5跑酷小游戏实现指南
1. 项目概述 本跑酷小游戏基于鸿蒙HarmonyOS 5开发,使用DevEco Studio作为开发工具,采用Java语言实现,包含角色控制、障碍物生成和分数计算系统。 2. 项目结构 /src/main/java/com/example/runner/├── MainAbilitySlice.java // 主界…...

Linux nano命令的基本使用
参考资料 GNU nanoを使いこなすnano基础 目录 一. 简介二. 文件打开2.1 普通方式打开文件2.2 只读方式打开文件 三. 文件查看3.1 打开文件时,显示行号3.2 翻页查看 四. 文件编辑4.1 Ctrl K 复制 和 Ctrl U 粘贴4.2 Alt/Esc U 撤回 五. 文件保存与退出5.1 Ctrl …...

破解路内监管盲区:免布线低位视频桩重塑停车管理新标准
城市路内停车管理常因行道树遮挡、高位设备盲区等问题,导致车牌识别率低、逃费率高,传统模式在复杂路段束手无策。免布线低位视频桩凭借超低视角部署与智能算法,正成为破局关键。该设备安装于车位侧方0.5-0.7米高度,直接规避树枝遮…...

uniapp 实现腾讯云IM群文件上传下载功能
UniApp 集成腾讯云IM实现群文件上传下载功能全攻略 一、功能背景与技术选型 在团队协作场景中,群文件共享是核心需求之一。本文将介绍如何基于腾讯云IMCOS,在uniapp中实现: 群内文件上传/下载文件元数据管理下载进度追踪跨平台文件预览 二…...

DBLP数据库是什么?
DBLP(Digital Bibliography & Library Project)Computer Science Bibliography是全球著名的计算机科学出版物的开放书目数据库。DBLP所收录的期刊和会议论文质量较高,数据库文献更新速度很快,很好地反映了国际计算机科学学术研…...

大模型——基于Docker+DeepSeek+Dify :搭建企业级本地私有化知识库超详细教程
基于Docker+DeepSeek+Dify :搭建企业级本地私有化知识库超详细教程 下载安装Docker Docker官网:https://www.docker.com/ 自定义Docker安装路径 Docker默认安装在C盘,大小大概2.9G,做这行最忌讳的就是安装软件全装C盘,所以我调整了下安装路径。 新建安装目录:E:\MyS…...
