dl转置卷积
转置卷积
转置卷积,顾名思义,通过名字我们应该就能看出来,其作用和卷积相反,它可以使得图像的像素增多
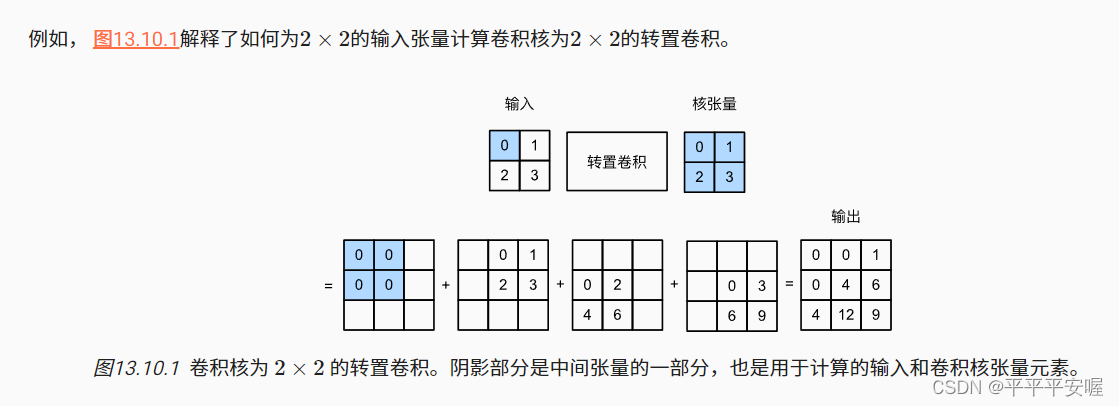
上图的意思是,输入是22的图像,卷积核为22的矩阵,然后变换成3*3的矩阵
代码如下
import torch
from torch import nn
from d2l import torch as d2ldef trans_conv(X, K): #X是原始矩阵,K是转置卷积核h, w = K.shapeY = torch.zeros((X.shape[0] + h - 1, X.shape[1] + w - 1)) # 转置卷积后的大小为x.shape[0] + k.shape[0] - 1 .........for i in range(X.shape[0]):for j in range(X.shape[1]):Y[i: i+h, j: j+w] += X[i, j] * Kreturn Y
X = torch.tensor([[0.0, 1.0], [2.0, 3.0]])
K = torch.tensor([[0.0, 1.0], [2.0, 3.0]])
trans_conv(X, K)
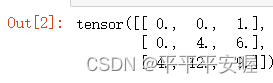
传统输入可能都是四维,使用API一样的
# 四维的话,调用API一样的
X, K = X.reshape(1, 1, 2, 2), K.reshape(1, 1, 2, 2)
tconv = nn.ConvTranspose2d(1, 1, kernel_size=2, bias=False)
tconv.weight.data = K
tconv(X)

与常规卷积不同,在转置卷积中,填充被应用于的输出(常规卷积将填充应用于输入)。
例如,当将高和宽两侧的填充数指定为1时,转置卷积的输出中将删除第一和最后的行与列。
换句话说,转置卷积的padding是删除输出的一圈
X, K = X.reshape(1, 1, 2, 2), K.reshape(1, 1, 2, 2)
tconv = nn.ConvTranspose2d(1, 1, kernel_size=2, padding=1, bias=False)
tconv.weight.data = K
tconv(X)

如果步幅为2的话,那么就会是一个4*4的矩阵
# 步幅为2的话那就是4*4了
X, K = X.reshape(1, 1, 2, 2), K.reshape(1, 1, 2, 2)
tconv = nn.ConvTranspose2d(1, 1, kernel_size=2, stride=2, bias=False)
tconv.weight.data = K
tconv(X)

对于多个输入和输出通道,转置卷积与常规卷积以相同方式运作。 假设输入有ci个通道,且转置卷积为每个输入通道分配了一个kwkh的卷积核张量。
当指定多个输出通道时,每个输出通道的卷积核shape为cikw*kh
接下来我们可能会想,转置卷积为何以矩阵变换命名呢?我们先来看看矩阵乘法如何实现卷积
这是传统卷积
X = torch.arange(9.0).reshape(3, 3)
K = torch.tensor([[1.0, 2.0], [3.0, 4.0]])
Y = d2l.corr2d(X, K)
Y
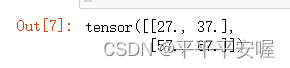
接下来通过矩阵乘法计算
# 先将K 写成稀疏权重矩阵
def kernel2matrix(K):k, W = torch.zeros(5), torch.zeros((4, 9)) # W是4*9的k[:2], k[3:5] = K[0, :], K[1, :]W[0, :5], W[1, 1:6], W[2, 3:8], W[3, 4:] = k, k, k, kreturn W
W = kernel2matrix(K)
W

# 然后就是矩阵乘法
Y == torch.matmul(W, X.reshape(-1)).reshape(2, 2)
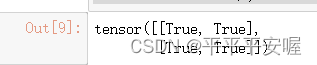
而如果我们用W的转置*Y,那就是原来的Y的转置卷积了
# 同样的,我们可以使用矩阵乘法来实现转置矩阵 Y 是卷积后的值
Z = trans_conv(Y, K)
Z == torch.matmul(W.T, Y.reshape(-1)).reshape(3, 3)
相关文章:

dl转置卷积
转置卷积 转置卷积,顾名思义,通过名字我们应该就能看出来,其作用和卷积相反,它可以使得图像的像素增多 上图的意思是,输入是22的图像,卷积核为22的矩阵,然后变换成3*3的矩阵 代码如下 import…...

详解结构体(包含结构体内存对齐,柔性数组,位段)【尊嘟很详细】
结构体 结构体是一些值的集合,这些值称为成员变量,结构的成员可以是标量、数组、指针,甚至是其他结构体。 成员名可以与程序中其它变量同名,互不干扰。 结构体的定义 (struct结构名{}) struct books {int a;c…...
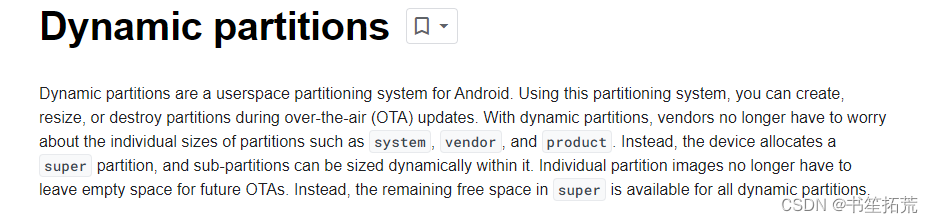
我的NPI项目之Android系统升级 - 同平台多产品的OTA
因为公司业务中涉及的面比较广泛,虽然都是提供移动终端PDA,但是使用的场景很多时候是不同的。例如,有提供给大型物流仓储的设备,对这样的设备必需具备扫码功能,键盘(戴手套操作),耐用…...

pnpm包管理器
官网 优点 快速 pnpm 比 npm 快了近 2 倍高效 node_modules 中的所有文件均克隆或硬链接自单一存储位置支持单体仓库 pnpm 内置了对单个源码仓库中包含多个软件包的支持权限严格 pnpm 创建的 node_modules 默认并非扁平结构,因此代码无法对任意软件包进行访问 安…...

flutter websocket发送ping包?
背景 服务端要求flutter客户端隔一段时间发送ping包,以此来建立心跳管理长连接。 代码 import package:web_socket_channel/io.dart; IOWebSocketChannel _channel IOWebSocketChannel.connect(Uri.parse(SocketService.url),pingInterval: const Duration(seco…...
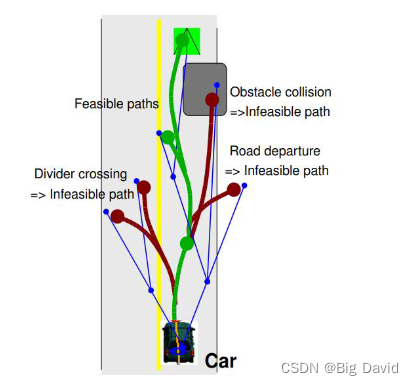
基于采样的自动驾驶规划算法 - PRM,RRT,RRT*,CL-RRT
本文将讲解PRM,RRT,RRT*自动驾驶规划算法原理,不正之处望读者指正 0 前言 机器人运动规划的基本任务:从开始位置到目标位置的运动 (1)如何躲避构型空间出现的障碍物 (2)如何满足机器…...
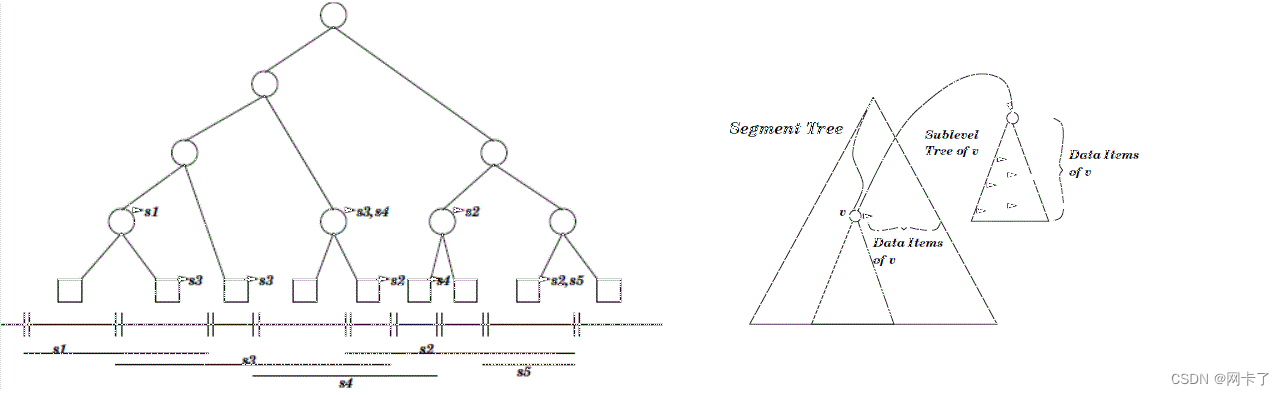
CGAL的D维范围树和线段树
范围树和线段树是两种数据结构,用于高效地处理和查询数据。 范围树(Range Tree)是一种二叉树,它通过递归地将每个节点分割成两个子节点来存储一个点集。每个节点表示一个范围,并且存储该范围内所有点的最小和最大值。范…...
005.HCIA 传输层
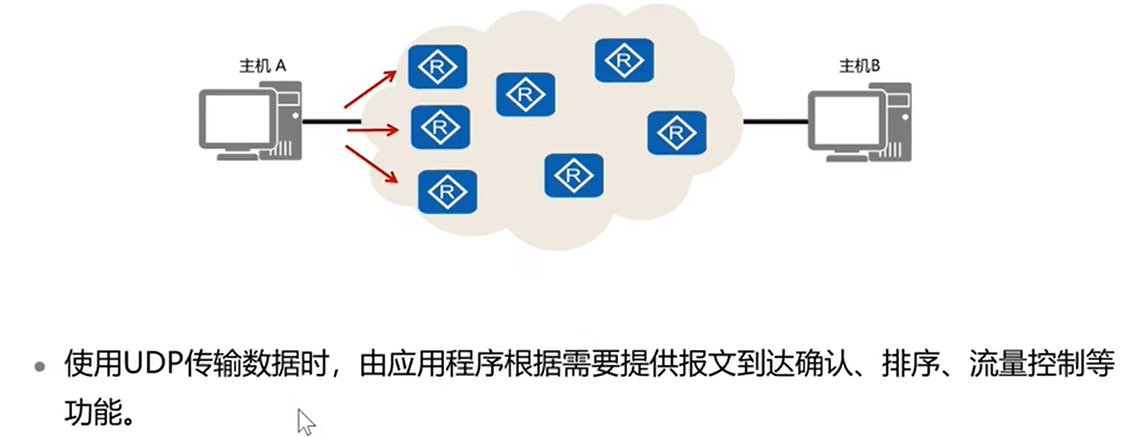
传输层定义了主机应用程序之间端到端的连通性。传输层中最为常见的两个协议分别是传输控制协议TCP (Transmission Control Protocol)和用户数据包协议UDP (User Datagram Protocol)。 1、相关概念 a. 传输层的端口 端口范围:0-65535 知名端口:0-1023&…...
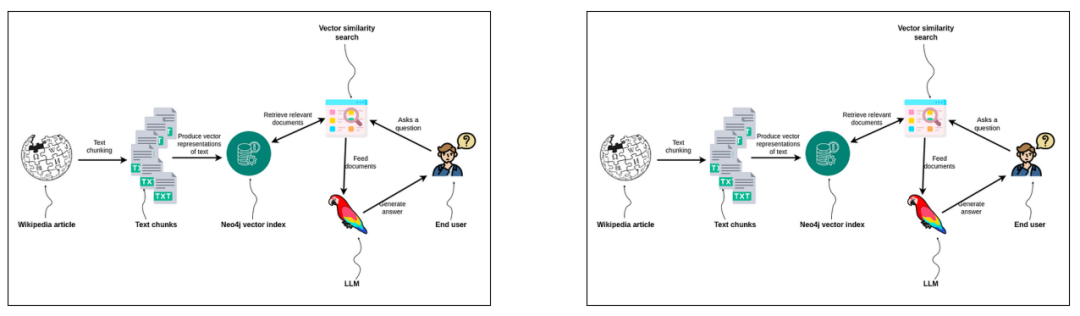
LLM之RAG实战(八)| 使用Neo4j和LlamaIndex实现多模态RAG
人工智能和大型语言模型领域正在迅速发展。一年前,没有人使用LLM来提高生产力。时至今日,很难想象我们大多数人或多或少都在使用LLM提供服务,从个人助手到文生图场景。由于大量的研究和兴趣,LLM每天都在变得越来越好、越来越聪明。…...
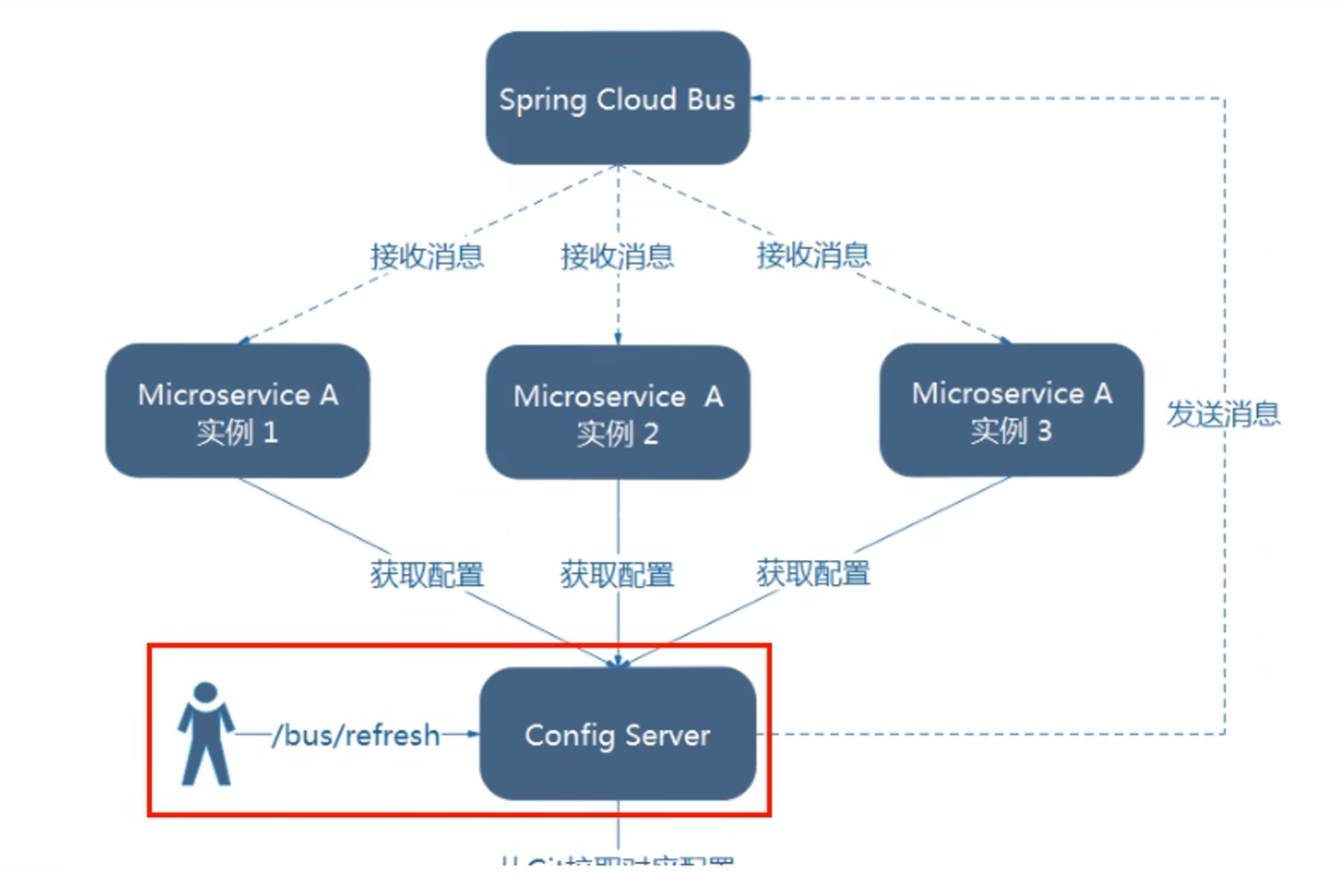
【SpringCloud笔记】(10)消息总线之Bus
Bus 前言 戳我了解Config 学习Config中我们遇到了一个问题: 当我们修改了GitHub上配置文件内容,微服务需要配置动态刷新并且需要手动向客户端发送post请求刷新微服务之后才能获取到GitHub修改过后的内容 假如有多个微服务客户端3355/3366/3377…等等…...

超酷的爬虫可视化界面
大家好,本文主要介绍使用tkinter获取本地文件夹、设置文本、创建按钮下拉框和对界面进行布局。 1.导入tkinter库 导入tkinter的库,可以使用ttkbootstrap美化生成的界面 ttkbootstrap官网地址:https://ttkbootstrap.readthedocs.io/en/late…...

【kafka消息里会有乱序消费的情况吗?如果有,是怎么解决的?】
文章目录 什么是消息乱序消费了?顺序生产,顺序存储,顺序消费如何解决乱序数据库乐观锁是怎么解决这个乱序问题吗 保证消息顺序消费两种方案固定分区方案乐观锁实现方案 前几天刷着视频看见评论区有大佬问了这个问题:你们的kafka消…...

【PID精讲12】基于MATLAB和Simulink的仿真教程
文章目录 写在前面一、基于Simulink的仿真1. 新建Simulink模型2. 保存Simulink模型3. 建模4. 运行二、基于MATLAB的仿真1. 编码2. 运行3. 调整曲线格式4. 导出图窗写在前面 第11讲介绍的连续系统的数字PID仿真是基于 Matlab的 M 语言实现的,对于初学者或者工程应用人员来说,…...

手机无人直播:解放直播的新方式
现如今,随着科技的迅猛发展,手机已经成为我们生活中不可或缺的一部分。除了通讯、娱乐等功能外,手机还能够通过直播功能将我们的生活实时分享给他人。而针对传统的直播方式,使用手机进行无人直播成为了一种全新的选择。 手机无人…...

ios 之 数据库、地理位置、应用内跳转、推送、制作静态库、CoreData
第一节:数据库 常见的API SQLite提供了一系列的API函数,用于执行各种数据库相关的操作。以下是一些常用的SQLite API函数及其简要说明:1. sqlite3_initialize:- 初始化SQLite库。通常在开始使用SQLite之前调用,但如果没有调用&a…...

Django(三)
1.快速上手 确保app已注册 【settings.py】 编写URL和视图函数对应关系 【urls.py】 编写视图函数 【views.py】 启动django项目 命令行启动python manage.py runserverPycharm启动 1.1 再写一个页面 2. templates模板 2.1 静态文件 2.1.1 static目录 2.1.2 引用静态…...
vscode括号颜色突然变成白色的了,怎么解决
更新版本后发现vscode的各种括号都变成了白色,由于分色括号已经使用习惯,突然变成白色非常不舒服,尝试多次后,为大家提供一下几种解决方式,希望能帮到同样受到此种困惑的你: 第一种: 首先打开…...

测试服务器带宽(ubuntu)
apt install python3 python3-pippip3 install speedtest-clispeestest-cli...
【WPF】使用Behavior以及ValidationRule实现表单校验
文章目录 使用ValidationRule实现检测用户输入EmptyValidationRule 非空校验TextBox设置非空校验TextBox设置非空校验并显示校验提示 结语 使用ValidationRule实现检测用户输入 EmptyValidationRule是TextBox内容是否为空校验,TextBox的Binding属性设置ValidationRu…...
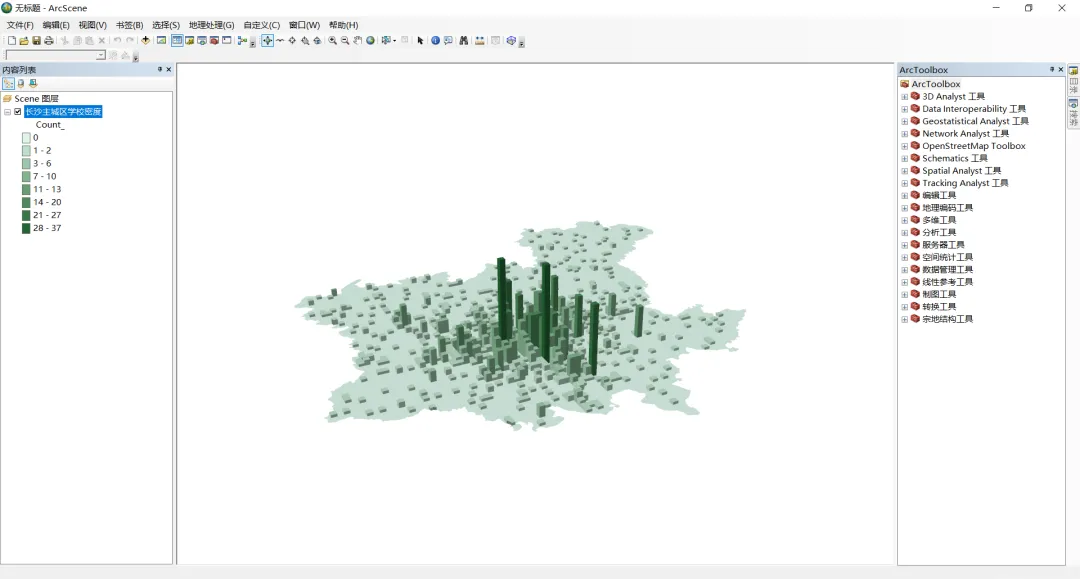
ArcGIS渔网的多种用法
在ArcGIS中有一个渔网工具,顾名思义,可以用来创建包含由矩形像元所组成网络的要素类。不太起眼,但它的用途却有很多,今天跟大家分享一篇关于渔网的多种用途。 1.马赛克地图制作 2.基于网格的设施密度统计制作马赛克地图 准备材…...

利用最小二乘法找圆心和半径
#include <iostream> #include <vector> #include <cmath> #include <Eigen/Dense> // 需安装Eigen库用于矩阵运算 // 定义点结构 struct Point { double x, y; Point(double x_, double y_) : x(x_), y(y_) {} }; // 最小二乘法求圆心和半径 …...

[特殊字符] 智能合约中的数据是如何在区块链中保持一致的?
🧠 智能合约中的数据是如何在区块链中保持一致的? 为什么所有区块链节点都能得出相同结果?合约调用这么复杂,状态真能保持一致吗?本篇带你从底层视角理解“状态一致性”的真相。 一、智能合约的数据存储在哪里…...

树莓派超全系列教程文档--(61)树莓派摄像头高级使用方法
树莓派摄像头高级使用方法 配置通过调谐文件来调整相机行为 使用多个摄像头安装 libcam 和 rpicam-apps依赖关系开发包 文章来源: http://raspberry.dns8844.cn/documentation 原文网址 配置 大多数用例自动工作,无需更改相机配置。但是,一…...
【机器视觉】单目测距——运动结构恢复
ps:图是随便找的,为了凑个封面 前言 在前面对光流法进行进一步改进,希望将2D光流推广至3D场景流时,发现2D转3D过程中存在尺度歧义问题,需要补全摄像头拍摄图像中缺失的深度信息,否则解空间不收敛…...
)
Android第十三次面试总结(四大 组件基础)
Activity生命周期和四大启动模式详解 一、Activity 生命周期 Activity 的生命周期由一系列回调方法组成,用于管理其创建、可见性、焦点和销毁过程。以下是核心方法及其调用时机: onCreate() 调用时机:Activity 首次创建时调用。…...

Fabric V2.5 通用溯源系统——增加图片上传与下载功能
fabric-trace项目在发布一年后,部署量已突破1000次,为支持更多场景,现新增支持图片信息上链,本文对图片上传、下载功能代码进行梳理,包含智能合约、后端、前端部分。 一、智能合约修改 为了增加图片信息上链溯源,需要对底层数据结构进行修改,在此对智能合约中的农产品数…...

Selenium常用函数介绍
目录 一,元素定位 1.1 cssSeector 1.2 xpath 二,操作测试对象 三,窗口 3.1 案例 3.2 窗口切换 3.3 窗口大小 3.4 屏幕截图 3.5 关闭窗口 四,弹窗 五,等待 六,导航 七,文件上传 …...

GO协程(Goroutine)问题总结
在使用Go语言来编写代码时,遇到的一些问题总结一下 [参考文档]:https://www.topgoer.com/%E5%B9%B6%E5%8F%91%E7%BC%96%E7%A8%8B/goroutine.html 1. main()函数默认的Goroutine 场景再现: 今天在看到这个教程的时候,在自己的电…...

全面解析数据库:从基础概念到前沿应用
在数字化时代,数据已成为企业和社会发展的核心资产,而数据库作为存储、管理和处理数据的关键工具,在各个领域发挥着举足轻重的作用。从电商平台的商品信息管理,到社交网络的用户数据存储,再到金融行业的交易记录处理&a…...

【深度学习新浪潮】什么是credit assignment problem?
Credit Assignment Problem(信用分配问题) 是机器学习,尤其是强化学习(RL)中的核心挑战之一,指的是如何将最终的奖励或惩罚准确地分配给导致该结果的各个中间动作或决策。在序列决策任务中,智能体执行一系列动作后获得一个最终奖励,但每个动作对最终结果的贡献程度往往…...
