[Ray Tracing: The Next Week] 笔记
前言
本篇博客参照自《Ray Tracing: The Next Week》教程,地址为:https://raytracing.github.io/books/RayTracingTheNextWeek.html
该教程在ray tracing in one weekend的基础上,增加了运动模糊、BVH树、Texture映射、柏林噪声、光照、体积渲染等内容。
渲染器的构建过程
与我的上一篇系列笔记类似,我会顺序罗列我认为重要的部分。
运动模糊
这一点和散焦模糊有些类似,也是模仿真实相机拍摄到的现象,即,当相机的快门按下时,运动的物体会发生模糊。
要实现这一点,方法是,在发射采样光线时,令光线在快门的这一段时间内随机发射,再混合采样结果。为光线增加了一个时间t属性。
于此同时,为场景种添加相应的运动物体,比如运动的球体,在1秒的时间内,球体会在某一个方向上移动。这时,因为光线包含时间属性,t时刻的光线r会打到在该时刻对应位置的物体表面上。
最后渲染时,则是将在快门这一时间段内所有的光线追踪结果混合。
以下是运动模糊的渲染结果:

BVH树
BVH树是一种空间划分的数据结构,可以有效提高光线与物体求交的效率。
在该教程中,BVH树的建立分为以下几步:
-
将所有图元包裹在一个大的包围盒中。
-
进行BVH树的划分。
-
一直分到BVH树的叶子节点只有一个图元为止。
作者在划分BVH树时,不希望留下空子树的问题,因此,在划分子树时,若当前只剩下一个图元,文中会令这个图元既属于左子树又属于右子树。另外,在划分过程中,对于[begin, end]范围内的图元,中点为mid,文中会将[begin, mid]划归左子树,[mid, end]划归右子树,相当于mid这个位置的图元既属于左子树又属于右子树。这种划分方式属于作者的喜好,有它的优势。
一个BVH树的例子如下:

包围盒
BVH树采用的包围盒应当便于计算相交,且紧密,AABB包围盒符合这个条件。
三维场景内的AABB包围盒为包含目标图元,且边平行于坐标轴的最小六面体。
如何计算射线与AABB包围盒的相交?拿二维场景举例,如下图所示,射线在与x的两个边界相交时,对应的相交位置为t1、t2,射线在与y的两个边界相交时,对应的相交位置为t3、t4,如果射线与这个2D AABB包围盒相交,则t1、t2与t3、t4 的范围重叠。

三维空间中与上述类似,当射线与x、y、z方向的对应平面相交时,如果范围有重合,则说明射线与包围盒相交。
如何求解射线与对应平面的交点?因为边界都是轴对齐的,将射线的方程带入对应边界的x、y或z值即可。
BVH树的划分
BVH树的划分主要分为三个步骤:
- 随机选择一个轴
- 对BVH树种的图元进行排序
- 对这些图元进行二分,构建子BVH树
文中给出的方法是每次随机选出一个轴,当然也可以轮流选择x、y、z轴。在排序时,依据的排序规则是每个图元对应轴的最小值。在C++中,可以构建box_x_compare、box_y_compare、box_z_compare,然后调用sort方法对数组进行排序。
最终,按照文中给出的BVH树构建方法,光线追踪的渲染过程有所加速。
纹理映射
在光线追踪中,纹理映射是一个反向寻找的过程,即通过射线与物体的交点,反向推算出交点在纹理中的颜色、凹凸等其他属性。这和光栅化不同,光栅化是通过纹理获得物体所有表面的颜色等属性,然后通过光栅化的过程投射给图像。
文中介绍了几种纹理,分别是纯色纹理、空间纹理、以及利用uv坐标的纹理。
纯色纹理。与uv坐标和空间坐标都无关,利用纯色纹理的材质,物体表面的所有颜色都一样。
空间纹理。采样和物体表面的空间坐标有关,和uv坐标无关,即物体表面某一点的颜色由该点的世界坐标(x, y, z)计算得出。
方格纹理就是一种空间纹理,对于任意一点,其颜色的计算是这样的:对于坐标(x, y, z),首先向下取整,得到三个整数结果(⌊x⌋,⌊y⌋,⌊z⌋),将这三个结果相加并进行模2运算,得到0或1。如果结果为0将映射到偶数颜色,如果结果为1将映射到奇数颜色。
方格纹理的一个例子如下:

利用uv坐标的纹理。需要知道如何根据物体表面的三维坐标,计算uv纹理坐标,再利用纹理坐标做颜色运算。因为场景中目前提供的模型都是球体,且目前也不涉及旋转,因此这里的uv坐标直接沿着球面计算。
球面的uv坐标用经纬度表示,其中u = Φ / 2π,v = θ / π,Φ为对应点在单位球中的经度,θ为对应点在单位球中的纬度。球面上点的三维关系与经纬度的关系如下:
y = − c o s ( θ ) x = − c o s ( ϕ ) s i n ( θ ) z = s i n ( ϕ ) s i n ( θ ) y = -cos(\theta)\\ x = -cos(\phi)sin(\theta)\\ z = sin(\phi)sin(\theta) y=−cos(θ)x=−cos(ϕ)sin(θ)z=sin(ϕ)sin(θ)
从而可得
ϕ = a t a n 2 ( − z , x ) + π θ = a r c c o s ( − y ) \phi = atan2(-z, x) + \pi\\ \theta = arccos(-y) ϕ=atan2(−z,x)+πθ=arccos(−y)
注意,这里因为atan2的数值范围为-π到π,但是为了让u映射到[0, 1]范围,需要加上一个π。
利用uv坐标的纹理效果如下:

柏林噪声
柏林噪声是一种自然噪声生成算法。文中主要利用柏林噪声生成空间纹理。
教程中一步步地给出3D柏林噪声的迭代改进过程。
第零次迭代,按照上述方格纹理的思路,首先生成一个大小为256的double数组ranfloat,其中的每个值为从0到1的随机。对于物体表面的每一个点,根据其三维坐标(x, y, z),得出一个指向ranfloat的下标,并根据这个下标,计算出方格的灰阶。其计算代码如下:
int i = static_cast<int>(4 * x) % 256;
int j = static_cast<int>(4 * y) % 256;
int k = static_cast<int>(4 * z) % 256;int index = i ^ j ^ k;
double grayscale = ranfloat[index];
这一步可以得出一种类似瓦片的效果,这种纹理是重复的。

第一次迭代,在上述瓦片贴图的基础上,加一些随机,具体到计算,主要是对上述代码中的i,j,k进行随机。这一部分的计算代码如下:
static int* perlin_generate_perm(){int p = new int[256];for(int i = 0;i<256;i++) p[i] = i;for(int i = 255;i>0;i--){int target = random_int(0, i); // 返回一个[0, i]范围的整数swap(p[i], p[target]);}return p;
}
// noise函数内部
{...int* perm_x = perlin_generate_perm();int* perm_y = perlin_generate_perm();int* perm_z = perlin_generate_perm();i = perm_x[i];j = perm_y[j];k = perm_z[k];...
}
这一步的纹理效果:

第二次迭代,在生成噪声时,进行线性插值。这一步是将一个点周围8个位置的值做平均加权运算,得出当前位置的灰阶。其核心计算代码如下:
static double trilinear_interp(double c[2][2][2], double u, double v, double w){double accum = 0.0;for (int i=0; i < 2; i++)for (int j=0; j < 2; j++)for (int k=0; k < 2; k++)accum += (i*u + (1-i)*(1-u))*(j*v + (1-j)*(1-v))*(k*w + (1-k)*(1-w))*c[i][j][k];return accum;
}// noise函数内部
{...int u = x - floor(x); // floor为向下取整运算int v = y - floor(y);int w = z - floor(z);int i = static_cast<int>(floor(x));int j = static_cast<int>(floor(y));int k = static_cast<int>(floor(z));double c[2][2][2];for(int di=0;di < 2;di++){for(int dj=0;dj<2;dj++){for(int dk=0;dk<2;dk++){c[di][dj][dk] = ranfloat[perm_x[(i+di) % 256] ^perm_y[(j+dj) % 256] ^perm_z[(k+dk) % 256]];}}}double grayscale = trilinear_interp(c, u, v, w);...
}
此时得出的结果:

第三次迭代,采用Hermitian插值,而不是线性插值来得到uvw的值,让结果更平滑,消除上述明显的网格特征。添加代码:
u = u*u*(3-2*u);
v = v*v*(3-2*v);
w = w*w*(3-2*w);
这一步得出的结果:

第四次迭代,调整噪声贴图的频率,方法就是将一个比例系数scale乘以(x, y, z)坐标值,scale越大,频率就越大。我的理解是,这种噪声的生成有一个模式,每经过一定的间隔就会得出相似的噪声结果。把坐标值增大,再来采样,等效于将模式的间隔缩小,这样导致的结果便是噪声图看起来频率更高。
这一步得出的效果如下:

第五次迭代,上面的结果看起来仍然有些块状,或许是因为这种模式的最小值和最大值总是恰好落在(x, y, z)都为整数的坐标上。因为当(x, y, z)为整数时,u, v, w的值均为0,此时trilinear_interp的结果为c[0][0][0],等于这个点没有和周围做平均运算。
可以用随机vec3数组ranvec代替之前的随机double数组ranfloat进行采样。在加权平均时,用权重向量和周围点的随机向量做点积,累加获得当前点的采样值。这样可以避免最小和最大值总是恰好落在整数坐标上。由于乘出来的值有可能小于零,需要做0.5 * (grayscale + 1.0)的归一化操作。
这一步的核心代码如下:
static double perlin_interp(vec3 c[2][2][2], double u, double v, double w) {double uu = u*u*(3-2*u);double vv = v*v*(3-2*v);double ww = w*w*(3-2*w);double accum = 0.0;for (int i=0; i < 2; i++)for (int j=0; j < 2; j++)for (int k=0; k < 2; k++) {vec3 weight_v(u-i, v-j, w-k);accum += (i*uu + (1-i)*(1-uu))* (j*vv + (1-j)*(1-vv))* (k*ww + (1-k)*(1-ww))* dot(c[i][j][k], weight_v);}return accum;
}
// noise函数内部
{...double u = x - floor(x);double v = y - floor(y);double w = z - floor(z);int i = static_cast<int>(floor(x));int j = static_cast<int>(floor(y));int k = static_cast<int>(floor(z));vec3 c[2][2][2];for (int di=0; di < 2; di++)for (int dj=0; dj < 2; dj++)for (int dk=0; dk < 2; dk++)c[di][dj][dk] = ranvec[perm_x[(i+di) % 256] ^perm_y[(j+dj) % 256] ^perm_z[(k+dk) % 256]];double grayscale = perlin_interp(c, u, v, w);...
}
这一步的结果如下图:

第六次迭代,制造湍流效果。将多个不同频率的噪声以不同的权重相加,这就是湍流。湍流部分的计算代码如下:
double turb(const point3& p, int depth=7) const {double accum = 0.0;double temp_p = p;double weight = 1.0;for (int i = 0; i < depth; i++) {accum += weight*noise(temp_p);weight *= 0.5;temp_p *= 2;}return fabs(accum);
}
这一步得出的效果如下:
注:这里的噪声图颜色很深,是因为这里的效果没有做归一化操作,而是直接把小于零的结果直接取绝对值了。

第七次,最后一次迭代,调整相位。将得出的灰度值送入正弦函数做计算,可以得到起伏的结果。利用相位迭代,可以实现类似大理石表面的纹理效果。这一步的核心代码如下:
double s = scale * p;
color = color(1,1,1) * 0.5 * (1 + sin(s.z() + 10*noise.turb(s)));
效果图如下:

平行四边形
除了球体之外,教程中终于添加了另外一种图元:平行四边形。
平行四边形用一个基点和两个向量表示:基点Q、两个边向量u和v。
如何实现射线与平行四边形的求交?主要分三步。
-
找到包含这个平行四边形的平面。
-
判断射线与这个平面的相交情况。
-
判断交点是否在这个平行四边形内。
找到四边形的平面
可以用u和v的叉乘得出平面法线,再将基点Q带入,便可得出这个平面方程。
判断射线与这个平面的相交
射线由一个基点和一个方向向量表示,判断射线与这个平面的相交,可以将射线的方程带入平面的方程。如果射线与平面平行或共面,则认为不相交,如果不平面,则求出这个交点,判断是否在射线的有效范围内。我们可以得到以下的式子。
平面方程: A x + B y + C z = D 射线方程: R ( t ) = P + t d 代入可得: n ∗ ( P + t d ) = D 解方程: n ∗ P + n ∗ t d = D n ∗ P + t ( n ∗ d ) = D t = D − n ∗ P n ∗ d 平面方程:Ax + By + Cz = D \ 射线方程:R(t) = \mathbf P + t\mathbf d\\ 代入可得:\mathbf n * (\mathbf P + t\mathbf d) = D \\ 解方程:\mathbf n *\mathbf P +\mathbf n * t\mathbf d = D\\ \mathbf n *\mathbf P + t(\mathbf n *\mathbf d) = D\\ t = \frac{D - \mathbf n * \mathbf P}{\mathbf n * \mathbf d} 平面方程:Ax+By+Cz=D 射线方程:R(t)=P+td代入可得:n∗(P+td)=D解方程:n∗P+n∗td=Dn∗P+t(n∗d)=Dt=n∗dD−n∗P
如果t属于射线范围[t_min, t_max]之内,则认为射线与这个平面相交。
判断交点是否在这个平行四边形内
将平面的点转换成以u、v为基底的二维坐标系中,对于任意一个点P,可以表示为P = Q + αu + βv。做以下运算:
令 p = P − Q = α u + β v , p 是从 Q 到 P 的向量 将 u 、 v 向量分别与 p 叉乘: v × p = α ( v × u ) + β ( v × v ) = α ( v × u ) u × p = α ( u × u ) + β ( u × v ) = β ( u × v ) 向量的除法不能直接进行,两边点乘 n n ∗ ( v × p ) = n ∗ α ( v × u ) n ∗ ( u × p ) = n ∗ β ( u × v ) 则 α = n ∗ ( v × p ) n ∗ ( v × u ) β = n ∗ ( u × p ) n ∗ ( u × v ) 令 w = n n ∗ ( u × v ) = n n ∗ n α = w ∗ ( p × v ) β = w ∗ ( u × p ) 令 p =\mathbf P -\mathbf Q = \alpha \mathbf u + \beta \mathbf v ,p是从Q到P的向量 \\ \\将u、v向量分别与p叉乘:\\ \mathbf v \times \mathbf p = \alpha (\mathbf v \times \mathbf u) + \beta (\mathbf v \times \mathbf v) = \alpha (\mathbf v \times \mathbf u)\\ \mathbf u \times \mathbf p = \alpha (\mathbf u \times \mathbf u) + \beta (\mathbf u \times \mathbf v) = \beta (\mathbf u \times \mathbf v)\\ \\ 向量的除法不能直接进行,两边点乘n\\ \mathbf n * (\mathbf v \times \mathbf p) = \mathbf n * \alpha (\mathbf v \times \mathbf u)\\ \mathbf n * (\mathbf u \times \mathbf p) = \mathbf n * \beta (\mathbf u \times \mathbf v)\\则 \\ \alpha = \frac{\mathbf n * (\mathbf v \times \mathbf p)}{\mathbf n * (\mathbf v \times \mathbf u)}\\ \beta = \frac{\mathbf n * (\mathbf u \times \mathbf p)}{\mathbf n * (\mathbf u \times \mathbf v)}\\ \\ 令 w = \frac{\mathbf n}{\mathbf n * (\mathbf u \times \mathbf v)} = \frac{\mathbf n}{\mathbf n * \mathbf n} \\ \alpha = \mathbf w * (\mathbf p \times \mathbf v)\\ \beta = \mathbf w * (\mathbf u \times \mathbf p) 令p=P−Q=αu+βv,p是从Q到P的向量将u、v向量分别与p叉乘:v×p=α(v×u)+β(v×v)=α(v×u)u×p=α(u×u)+β(u×v)=β(u×v)向量的除法不能直接进行,两边点乘nn∗(v×p)=n∗α(v×u)n∗(u×p)=n∗β(u×v)则α=n∗(v×u)n∗(v×p)β=n∗(u×v)n∗(u×p)令w=n∗(u×v)n=n∗nnα=w∗(p×v)β=w∗(u×p)
要判断点是否在平行四边形中,判断α和β在[0, 1]范围内即可。
平行四边形的绘制结果:

灯光
文中将能发光的特性作为一个灯光材质。
灯光材质会有一个主动发光的函数,这样在光线打到灯光材质表面时,会增加一项主动发光所产生的颜色。对于不发光的材质而言,主动发光产生的颜色为零。
同时设置背景颜色,当射线最终没有打到物体时,赋予默认背景颜色,而不是根据画布位置得出的渐变色。
得到的灯光效果如下:

实例化
这一部分主要引入了模型的移动和旋转。
所谓实例是已放置到场景中的几何图元的副本,它完全独立于图元的其他副本,并且可以移动或旋转。
模型移动
在这个过程的实现中,文中没有直接移动模型的坐标,而是反向变换光线的原点位置,然后与模型做求交运算。具体而言,主要分为以下三步:
-
将射线的原点反向移动偏移量
-
判断添加偏移后的射线是否与物体存在交点(如果存在,判断在何处)
-
给交点的位置增加偏移量
这一过程也可以从坐标变化的角度来思考:
- 将射线从世界坐标系转换到物体局部坐标系
- 判断射线在物体坐标系内是否与物体存在交点(如果存在,判断在何处)
- 将交点从物体局部坐标系转换到世界坐标系
文中将移动封装成了一个可击中对象,相当于构建了一个实例,这部分的代码如下:
class translate : public hittable {public:bool hit(const ray& r, interval ray_t, hit_record& rec) const override {// 将射线的原点反向移动偏移量ray offset_r(r.origin() - offset, r.direction(), r.time());// 判断添加偏移后的射线是否与物体存在交点(如果存在,判断在何处)if (!object->hit(offset_r, ray_t, rec))return false;// 给交点的位置增加偏移量rec.p += offset;return true;}private:shared_ptr<hittable> object;vec3 offset;
};
模型旋转
模型的旋转与上述的构建过程类似,不过稍微复杂。
文中给出的旋转表示方法是欧拉角表示法。当射线变换到有旋转的物体坐标系时,不仅原点位置改变,射线的方向也会改变。这一过程如下:
- 将光线的原点和方向从世界坐标系变换到物体坐标系
- 判断光线在物体坐标系内与物体是否相交以及交点在何处
- 将交点的位置以及交点处的法线从物体坐标系变换到世界坐标系
旋转同样被封装成了一个可击中对象,相当于一个实例,这部分的核心代码如下:
class rotate_y : public hittable {public:bool hit(const ray& r, interval ray_t, hit_record& rec) const override {// 将光线从世界坐标系转换到物体局部坐标系auto origin = r.origin();auto direction = r.direction();origin[0] = cos_theta*r.origin()[0] - sin_theta*r.origin()[2];origin[2] = sin_theta*r.origin()[0] + cos_theta*r.origin()[2];direction[0] = cos_theta*r.direction()[0] - sin_theta*r.direction()[2];direction[2] = sin_theta*r.direction()[0] + cos_theta*r.direction()[2];ray rotated_r(origin, direction, r.time());// 判断是否有交点以及交点在何处if (!object->hit(rotated_r, ray_t, rec))return false;// 将交点从物体局部坐标系转换到世界坐标系auto p = rec.p;p[0] = cos_theta*rec.p[0] + sin_theta*rec.p[2];p[2] = -sin_theta*rec.p[0] + cos_theta*rec.p[2];// 将交点处的法线从物体局部坐标系转换到世界坐标系auto normal = rec.normalnormal[0] = cos_theta*rec.normal[0] + sin_theta*rec.normal[2];normal[2] = -sin_theta*rec.normal[0] + cos_theta*rec.normal[2];rec.p = p;rec.normal = normal;return true;}
};
运用平移和旋转,渲染出的cornell场景如下:

体积物体
这一部分将的是对于类似雾这种对象的光线追踪渲染,不过为了简便,文中只举例了密度恒定,且边界不变的情况。
光线在射向这类物体时,有概率直接穿透,也有概率散射开来。

对于这样的物体,文中主要设置了两种参数,一个是密度,另一个是边界。
在做射线求交运算时,会设置计算两个碰撞点,分别代表射入和射出的点,并根据密度参数和随机值,计算得出一个新的碰撞点,用来做计算。如果这个点不在体积内,则判定这个射线没有和物体相交,如果在体积内,则判定为相交,进行计算。
判定相交时,射入的光线会在碰撞点处随机散射。
这一步的渲染效果:
最终效果
和上一部教程一样,作者给出了一个大场景,渲染出一个最终效果。
这里我为了能够尽快得出渲染结果,将采样次数降低,牺牲了质量,此时的渲染结果如下:

完整代码
这一次同样上传在网盘上:
链接:https://pan.baidu.com/s/1hspYR2VGNlxynRJYa9jHug?pwd=qyfj
提取码:qyfj
–来自百度网盘超级会员V6的分享
ps: 只分享了源码,没有什么依赖库,应该可以直接跑出ppm格式的图片。
参考
https://www.cnblogs.com/wickedpriest/p/12269564.html
https://baike.baidu.com/item/%E5%8C%85%E5%9B%B4%E7%9B%92/4562345
https://blog.csdn.net/weixin_44176696/article/details/118655688
相关文章:

[Ray Tracing: The Next Week] 笔记
前言 本篇博客参照自《Ray Tracing: The Next Week》教程,地址为:https://raytracing.github.io/books/RayTracingTheNextWeek.html 该教程在ray tracing in one weekend的基础上,增加了运动模糊、BVH树、Texture映射、柏林噪声、光照、体积…...
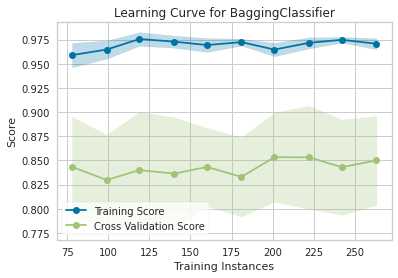
企业级实战项目:基于 pycaret 自动化预测公司是否破产
本文系数据挖掘实战系列文章,我跟大家分享一个数据挖掘实战,与以往的数据实战不同的是,用自动机器学习方法完成模型构建与调优部分工作,深入理解由此带来的便利与效果。 1. Introduction 本文是一篇数据挖掘实战案例,…...
dl转置卷积
转置卷积 转置卷积,顾名思义,通过名字我们应该就能看出来,其作用和卷积相反,它可以使得图像的像素增多 上图的意思是,输入是22的图像,卷积核为22的矩阵,然后变换成3*3的矩阵 代码如下 import…...

详解结构体(包含结构体内存对齐,柔性数组,位段)【尊嘟很详细】
结构体 结构体是一些值的集合,这些值称为成员变量,结构的成员可以是标量、数组、指针,甚至是其他结构体。 成员名可以与程序中其它变量同名,互不干扰。 结构体的定义 (struct结构名{}) struct books {int a;c…...
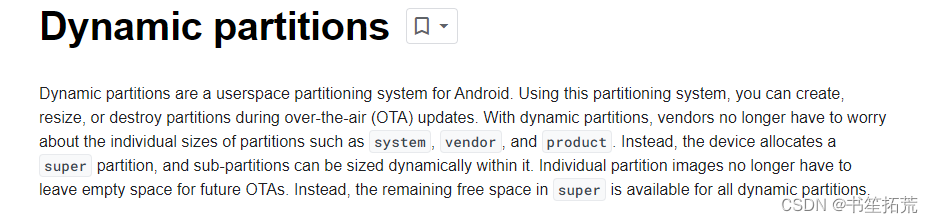
我的NPI项目之Android系统升级 - 同平台多产品的OTA
因为公司业务中涉及的面比较广泛,虽然都是提供移动终端PDA,但是使用的场景很多时候是不同的。例如,有提供给大型物流仓储的设备,对这样的设备必需具备扫码功能,键盘(戴手套操作),耐用…...

pnpm包管理器
官网 优点 快速 pnpm 比 npm 快了近 2 倍高效 node_modules 中的所有文件均克隆或硬链接自单一存储位置支持单体仓库 pnpm 内置了对单个源码仓库中包含多个软件包的支持权限严格 pnpm 创建的 node_modules 默认并非扁平结构,因此代码无法对任意软件包进行访问 安…...

flutter websocket发送ping包?
背景 服务端要求flutter客户端隔一段时间发送ping包,以此来建立心跳管理长连接。 代码 import package:web_socket_channel/io.dart; IOWebSocketChannel _channel IOWebSocketChannel.connect(Uri.parse(SocketService.url),pingInterval: const Duration(seco…...
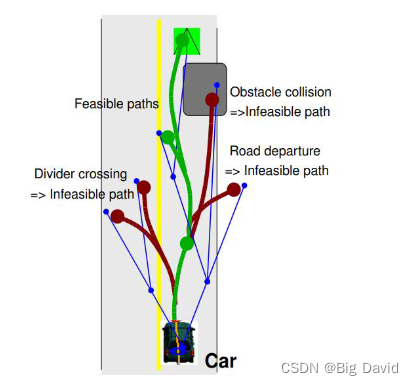
基于采样的自动驾驶规划算法 - PRM,RRT,RRT*,CL-RRT
本文将讲解PRM,RRT,RRT*自动驾驶规划算法原理,不正之处望读者指正 0 前言 机器人运动规划的基本任务:从开始位置到目标位置的运动 (1)如何躲避构型空间出现的障碍物 (2)如何满足机器…...
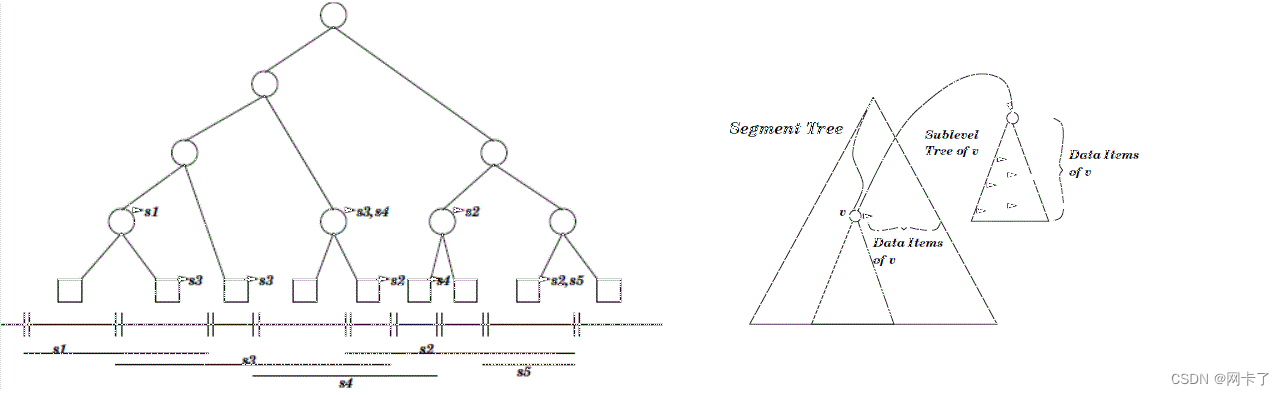
CGAL的D维范围树和线段树
范围树和线段树是两种数据结构,用于高效地处理和查询数据。 范围树(Range Tree)是一种二叉树,它通过递归地将每个节点分割成两个子节点来存储一个点集。每个节点表示一个范围,并且存储该范围内所有点的最小和最大值。范…...
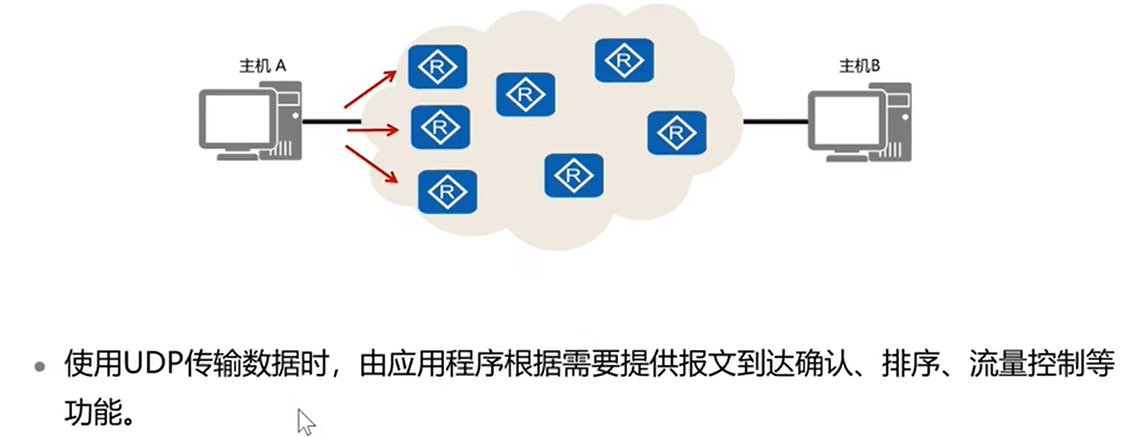
005.HCIA 传输层
传输层定义了主机应用程序之间端到端的连通性。传输层中最为常见的两个协议分别是传输控制协议TCP (Transmission Control Protocol)和用户数据包协议UDP (User Datagram Protocol)。 1、相关概念 a. 传输层的端口 端口范围:0-65535 知名端口:0-1023&…...
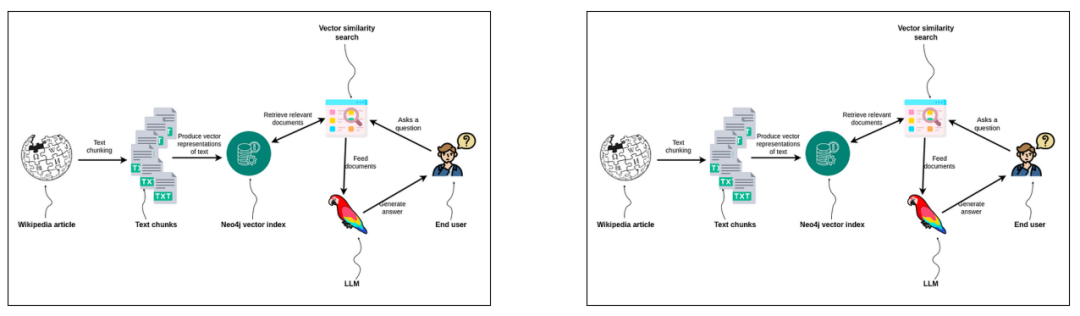
LLM之RAG实战(八)| 使用Neo4j和LlamaIndex实现多模态RAG
人工智能和大型语言模型领域正在迅速发展。一年前,没有人使用LLM来提高生产力。时至今日,很难想象我们大多数人或多或少都在使用LLM提供服务,从个人助手到文生图场景。由于大量的研究和兴趣,LLM每天都在变得越来越好、越来越聪明。…...
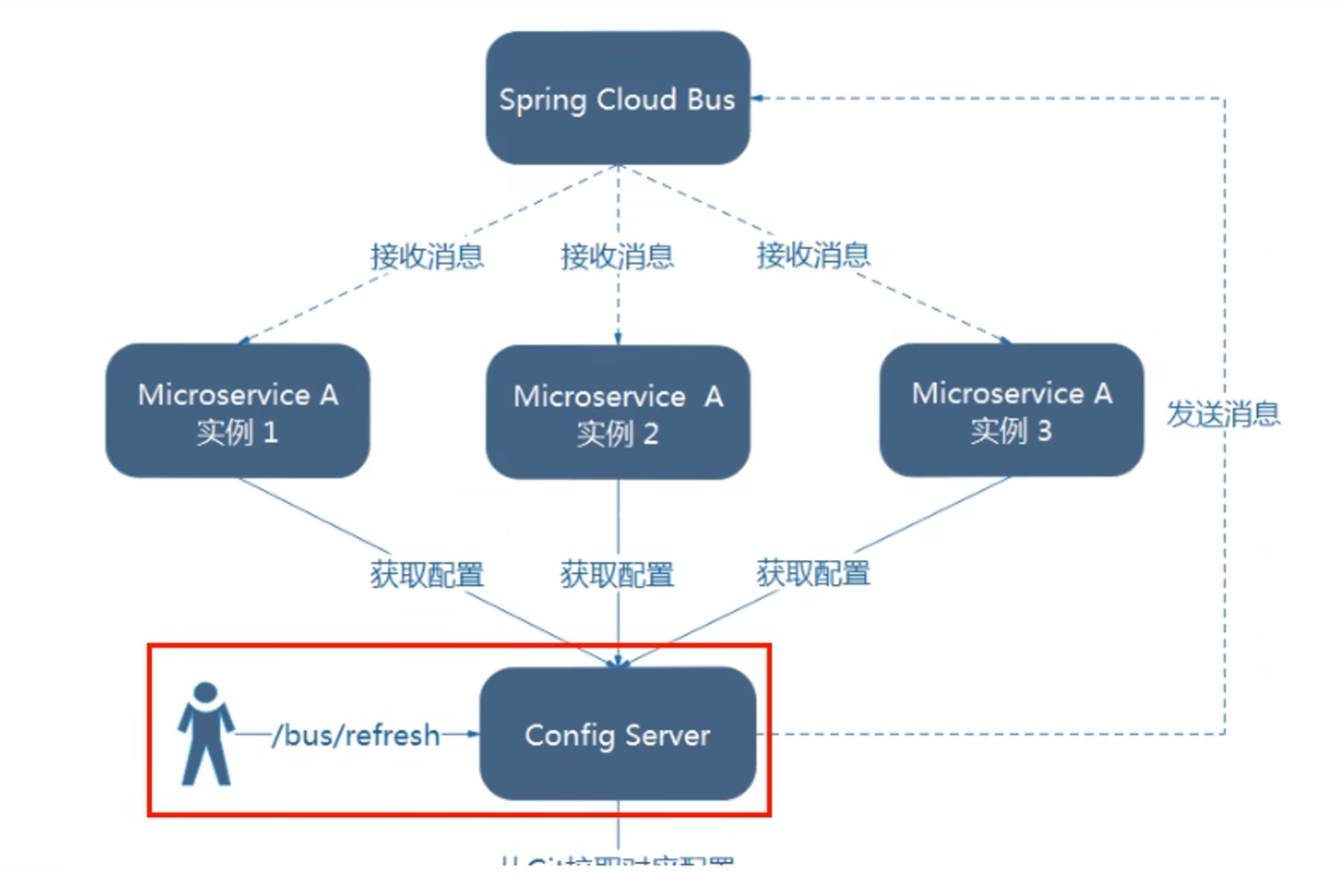
【SpringCloud笔记】(10)消息总线之Bus
Bus 前言 戳我了解Config 学习Config中我们遇到了一个问题: 当我们修改了GitHub上配置文件内容,微服务需要配置动态刷新并且需要手动向客户端发送post请求刷新微服务之后才能获取到GitHub修改过后的内容 假如有多个微服务客户端3355/3366/3377…等等…...

超酷的爬虫可视化界面
大家好,本文主要介绍使用tkinter获取本地文件夹、设置文本、创建按钮下拉框和对界面进行布局。 1.导入tkinter库 导入tkinter的库,可以使用ttkbootstrap美化生成的界面 ttkbootstrap官网地址:https://ttkbootstrap.readthedocs.io/en/late…...

【kafka消息里会有乱序消费的情况吗?如果有,是怎么解决的?】
文章目录 什么是消息乱序消费了?顺序生产,顺序存储,顺序消费如何解决乱序数据库乐观锁是怎么解决这个乱序问题吗 保证消息顺序消费两种方案固定分区方案乐观锁实现方案 前几天刷着视频看见评论区有大佬问了这个问题:你们的kafka消…...

【PID精讲12】基于MATLAB和Simulink的仿真教程
文章目录 写在前面一、基于Simulink的仿真1. 新建Simulink模型2. 保存Simulink模型3. 建模4. 运行二、基于MATLAB的仿真1. 编码2. 运行3. 调整曲线格式4. 导出图窗写在前面 第11讲介绍的连续系统的数字PID仿真是基于 Matlab的 M 语言实现的,对于初学者或者工程应用人员来说,…...

手机无人直播:解放直播的新方式
现如今,随着科技的迅猛发展,手机已经成为我们生活中不可或缺的一部分。除了通讯、娱乐等功能外,手机还能够通过直播功能将我们的生活实时分享给他人。而针对传统的直播方式,使用手机进行无人直播成为了一种全新的选择。 手机无人…...

ios 之 数据库、地理位置、应用内跳转、推送、制作静态库、CoreData
第一节:数据库 常见的API SQLite提供了一系列的API函数,用于执行各种数据库相关的操作。以下是一些常用的SQLite API函数及其简要说明:1. sqlite3_initialize:- 初始化SQLite库。通常在开始使用SQLite之前调用,但如果没有调用&a…...

Django(三)
1.快速上手 确保app已注册 【settings.py】 编写URL和视图函数对应关系 【urls.py】 编写视图函数 【views.py】 启动django项目 命令行启动python manage.py runserverPycharm启动 1.1 再写一个页面 2. templates模板 2.1 静态文件 2.1.1 static目录 2.1.2 引用静态…...
vscode括号颜色突然变成白色的了,怎么解决
更新版本后发现vscode的各种括号都变成了白色,由于分色括号已经使用习惯,突然变成白色非常不舒服,尝试多次后,为大家提供一下几种解决方式,希望能帮到同样受到此种困惑的你: 第一种: 首先打开…...

测试服务器带宽(ubuntu)
apt install python3 python3-pippip3 install speedtest-clispeestest-cli...

<6>-MySQL表的增删查改
目录 一,create(创建表) 二,retrieve(查询表) 1,select列 2,where条件 三,update(更新表) 四,delete(删除表…...

OkHttp 中实现断点续传 demo
在 OkHttp 中实现断点续传主要通过以下步骤完成,核心是利用 HTTP 协议的 Range 请求头指定下载范围: 实现原理 Range 请求头:向服务器请求文件的特定字节范围(如 Range: bytes1024-) 本地文件记录:保存已…...

React19源码系列之 事件插件系统
事件类别 事件类型 定义 文档 Event Event 接口表示在 EventTarget 上出现的事件。 Event - Web API | MDN UIEvent UIEvent 接口表示简单的用户界面事件。 UIEvent - Web API | MDN KeyboardEvent KeyboardEvent 对象描述了用户与键盘的交互。 KeyboardEvent - Web…...
:爬虫完整流程)
Python爬虫(二):爬虫完整流程
爬虫完整流程详解(7大核心步骤实战技巧) 一、爬虫完整工作流程 以下是爬虫开发的完整流程,我将结合具体技术点和实战经验展开说明: 1. 目标分析与前期准备 网站技术分析: 使用浏览器开发者工具(F12&…...

全面解析各类VPN技术:GRE、IPsec、L2TP、SSL与MPLS VPN对比
目录 引言 VPN技术概述 GRE VPN 3.1 GRE封装结构 3.2 GRE的应用场景 GRE over IPsec 4.1 GRE over IPsec封装结构 4.2 为什么使用GRE over IPsec? IPsec VPN 5.1 IPsec传输模式(Transport Mode) 5.2 IPsec隧道模式(Tunne…...

GC1808高性能24位立体声音频ADC芯片解析
1. 芯片概述 GC1808是一款24位立体声音频模数转换器(ADC),支持8kHz~96kHz采样率,集成Δ-Σ调制器、数字抗混叠滤波器和高通滤波器,适用于高保真音频采集场景。 2. 核心特性 高精度:24位分辨率,…...

20个超级好用的 CSS 动画库
分享 20 个最佳 CSS 动画库。 它们中的大多数将生成纯 CSS 代码,而不需要任何外部库。 1.Animate.css 一个开箱即用型的跨浏览器动画库,可供你在项目中使用。 2.Magic Animations CSS3 一组简单的动画,可以包含在你的网页或应用项目中。 3.An…...

SQL慢可能是触发了ring buffer
简介 最近在进行 postgresql 性能排查的时候,发现 PG 在某一个时间并行执行的 SQL 变得特别慢。最后通过监控监观察到并行发起得时间 buffers_alloc 就急速上升,且低水位伴随在整个慢 SQL,一直是 buferIO 的等待事件,此时也没有其他会话的争抢。SQL 虽然不是高效 SQL ,但…...
)
C++课设:简易日历程序(支持传统节假日 + 二十四节气 + 个人纪念日管理)
名人说:路漫漫其修远兮,吾将上下而求索。—— 屈原《离骚》 创作者:Code_流苏(CSDN)(一个喜欢古诗词和编程的Coder😊) 专栏介绍:《编程项目实战》 目录 一、为什么要开发一个日历程序?1. 深入理解时间算法2. 练习面向对象设计3. 学习数据结构应用二、核心算法深度解析…...

【C++进阶篇】智能指针
C内存管理终极指南:智能指针从入门到源码剖析 一. 智能指针1.1 auto_ptr1.2 unique_ptr1.3 shared_ptr1.4 make_shared 二. 原理三. shared_ptr循环引用问题三. 线程安全问题四. 内存泄漏4.1 什么是内存泄漏4.2 危害4.3 避免内存泄漏 五. 最后 一. 智能指针 智能指…...
