sklearn 逻辑回归Demo
逻辑回归案例
假设表示
基于上述情况,要使分类器的输出在[0,1]之间,可以采用假设表示的方法。
设 h θ ( x ) = g ( θ T x ) h_θ (x)=g(θ^T x) hθ(x)=g(θTx),
其中 g ( z ) = 1 ( 1 + e − z ) g(z)=\frac{1}{(1+e^{−z} )} g(z)=(1+e−z)1, 称为逻辑函数(Sigmoid function,又称为激活函数,生物学上的S型曲线)
h θ ( x ) = 1 ( 1 + e − θ T X ) h_θ (x)=\frac{1}{(1+e^{−θ^T X} )} hθ(x)=(1+e−θTX)1
其两条渐近线分别为h(x)=0和h(x)=1
在分类条件下,最终的输出结果是:
h θ ( x ) = P ( y = 1 │ x , θ ) h_θ (x)=P(y=1│x,θ) hθ(x)=P(y=1│x,θ)
其代表在给定x的条件下 其y=1的概率
P ( y = 1 │ x , θ ) + P ( y = 0 │ x , θ ) = 1 P(y=1│x,θ)+P(y=0│x,θ)=1 P(y=1│x,θ)+P(y=0│x,θ)=1
决策边界( Decision boundary)
对假设函数设定阈值 h ( x ) = 0.5 h(x)=0.5 h(x)=0.5,
当 h ( x ) ≥ 0.5 h(x)≥0.5 h(x)≥0.5 时,输出结果y=1.
根据假设函数的性质,当 x ≥ 0 时, x≥0时, x≥0时,h(x)≥0.5
用 θ T x θ^T x θTx替换x,则当 θ T x ≥ 0 θ^T x≥0 θTx≥0时, h ( x ) ≥ 0.5 , y = 1 h(x)≥0.5,y=1 h(x)≥0.5,y=1
解出 θ T x ≥ 0 θ^T x≥0 θTx≥0,其答案将会是一个在每一个 x i x_i xi轴上都有的不等式函数。
这个不等式函数将整个空间分成了y=1 和 y=0的两个部分,称之为决策边界。
激活函数的代价函数
在线性回归中的代价函数:
J ( θ ) = 1 m ∑ i = 1 m 1 2 ( h θ ( x ( i ) ) − y ( i ) ) 2 J(θ)=\frac{1}{m}∑_{i=1}^m \frac{1}{2} (h_θ (x^{(i)} )−y^{(i)} )^2 J(θ)=m1i=1∑m21(hθ(x(i))−y(i))2
令 C o s t ( h θ ( x ) , y ) = 1 2 ( h θ ( x ( i ) ) − y ( i ) ) 2 Cost(hθ (x),y)=\frac{1}{2}(h_θ (x^{(i)} )−y^{(i)} )^2 Cost(hθ(x),y)=21(hθ(x(i))−y(i))2,
Cost是一个非凹函数,有许多的局部最小值,不利于使用梯度下降法。对于分类算法,设置其代价函数为:
J ( θ ) = − 1 m ∑ i = 1 m [ y ( i ) l o g ( h θ ( x ( i ) ) ) − ( 1 − y ( i ) ) ∗ l o g ( 1 − h θ ( x ( i ) ) ) ] J(θ)=-\frac{1}{m}∑_{i=1}^m [y^{(i)}log(h_θ (x^{(i)}) )−(1-y^{(i)})*log(1-h_θ (x^{(i)}))] J(θ)=−m1i=1∑m[y(i)log(hθ(x(i)))−(1−y(i))∗log(1−hθ(x(i)))]
对其化简:
C o s t ( h θ ( x ) , y ) = − y l o g ( h θ ( x ) ) − ( ( 1 − y ) l o g ( 1 − h θ ( x ) ) ) Cost(h_θ (x),y)=−ylog(h_θ (x))−((1−y)log(1−h_θ (x))) Cost(hθ(x),y)=−ylog(hθ(x))−((1−y)log(1−hθ(x)))
检验:
当 y = 1 y=1 y=1时, − l o g ( h θ ( x ) ) −log(h_θ (x)) −log(hθ(x))
当 y = 0 y=0 y=0时, − l o g ( 1 − h θ ( x ) ) −log(1−h_θ (x)) −log(1−hθ(x))
那么代价函数可以写成:
J ( θ ) = − 1 m [ ∑ i = 1 m y ( i ) l o g ( h θ ( x ( i ) ) ) + ( 1 − y ( i ) ) l o g ( 1 − h θ ( x ( i ) ) ) ] J(θ)=-\frac{1}{m}[∑_{i=1}^m y^{(i)} log(h_θ(x^{(i)} ))+(1−y^{(i)}) log(1−h_θ (x^{(i)}))] J(θ)=−m1[i=1∑my(i)log(hθ(x(i)))+(1−y(i))log(1−hθ(x(i)))]
对于代价函数,采用梯度下降算法求θ的最小值:
θ j ≔ θ j − α ∂ J ( θ ) ∂ θ j θ_j≔θ_j−α\frac{∂J(θ)}{∂θ_j} θj:=θj−α∂θj∂J(θ)
代入梯度:
θ j ≔ θ j − α ∑ i = 1 m ( h θ ( x ( i ) ) − y ( i ) ) x j i θ_j≔θ_j−α∑_{i=1}^m(h_θ (x^{(i)} )−y^{(i)} ) x_j^i θj:=θj−αi=1∑m(hθ(x(i))−y(i))xji
sklearn 代码
导入库
## 基础函数库
import numpy as np ## 导入画图库
import matplotlib.pyplot as plt## 导入逻辑回归模型函数
from sklearn.linear_model import LogisticRegression
模型训练
## 构造数据集
x_fearures = np.array([[-1, -2], [-2, -1], [-3, -2], [1, 3], [2, 1], [3, 2]])
y_label = np.array([0, 0, 0, 1, 1, 1])## 调用逻辑回归模型
lr_clf = LogisticRegression()## 用逻辑回归模型拟合构造的数据集
lr_clf = lr_clf.fit(x_fearures, y_label) #其拟合方程为 y=w0+w1*x1+w2*x2
模型参数查看
## 查看其对应模型的w
print('the weight of Logistic Regression:',lr_clf.coef_)## 查看其对应模型的w0
print('the intercept(w0) of Logistic Regression:',lr_clf.intercept_)

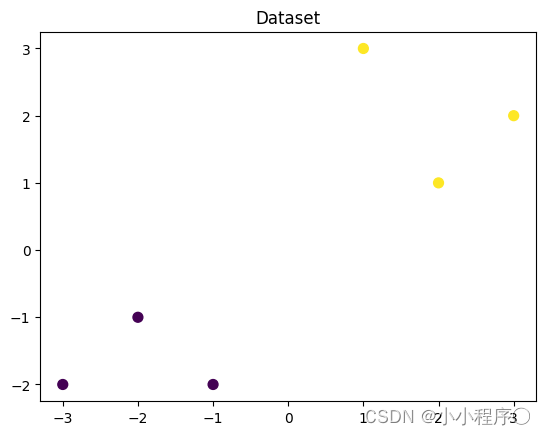
可视化构造的数据样本点
plt.figure()
plt.scatter(x_fearures[:,0],x_fearures[:,1], c=y_label, s=50, cmap='viridis')
plt.title('Dataset')
plt.show()
模型预测
## 在训练集和测试集上分别利用训练好的模型进行预测
y_label_new1_predict = lr_clf.predict(x_fearures_new1)
y_label_new2_predict = lr_clf.predict(x_fearures_new2)print('The New point 1 predict class:\n',y_label_new1_predict)
print('The New point 2 predict class:\n',y_label_new2_predict)## 由于逻辑回归模型是概率预测模型(前文介绍的 p = p(y=1|x,\theta)),所以我们可以利用 predict_proba 函数预测其概率
y_label_new1_predict_proba = lr_clf.predict_proba(x_fearures_new1)
y_label_new2_predict_proba = lr_clf.predict_proba(x_fearures_new2)print('The New point 1 predict Probability of each class:\n',y_label_new1_predict_proba)
print('The New point 2 predict Probability of each class:\n',y_label_new2_predict_proba)

相关文章:

sklearn 逻辑回归Demo
逻辑回归案例 假设表示 基于上述情况,要使分类器的输出在[0,1]之间,可以采用假设表示的方法。 设 h θ ( x ) g ( θ T x ) h_θ (x)g(θ^T x) hθ(x)g(θTx), 其中 g ( z ) 1 ( 1 e − z ) g(z)\frac{1}{(1e^{−z} )} g(z)(1e−z)1…...

什么是众创空间?他有什么特点?
众创空间,是一种为大众创新创业提供专业化服务的创业服务平台,是顺应网络时代创新创业特点和需求,通过市场化机制、专业化服务和资本化途径构建的低成本、便利化、全要素、开放式的新型创业服务平台的统称。众创空间包括创客空间、联合办公空…...

什么是数据分析思维
参考 一文学会如何做电商数据分析(附运营分析指标框架) 电子商务该如何做数据分析?如何数据分析入门(从各项指标表象进入) https://www.processon.com/outline/6589838c3129f1550cc69950 数据分析步骤 什么是数据分析…...
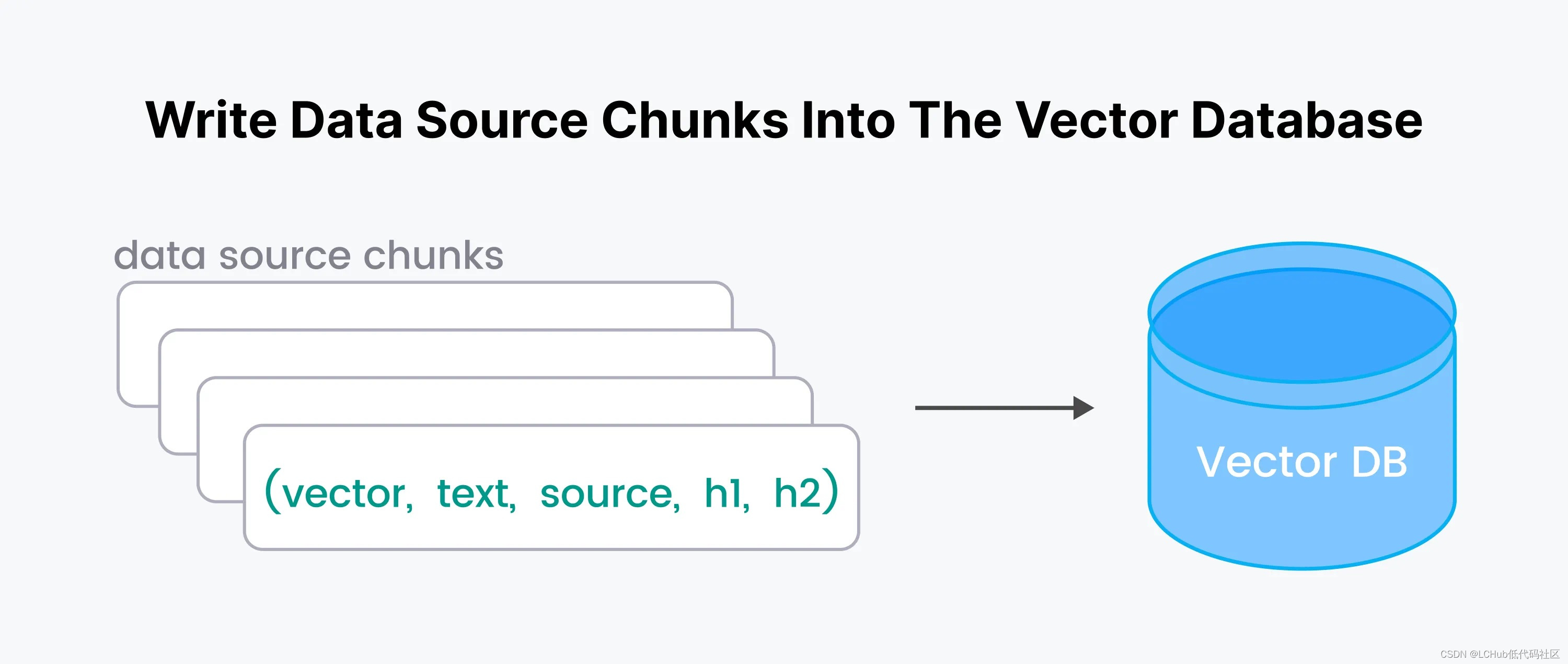
利用Milvus Cloud和LangChain构建机器人:一种引人入胜且通俗易懂的方法
一、引言 机器人已经深入我们的日常生活,从家庭服务到工业生产,再到医疗和运输等领域。然而,这些机器人往往需要复杂的算法和数据处理技术才能有效地执行任务。在这个过程中,人工智能(AI)和机器学习&#…...

数据结构-如何实现一个队列?逐步解析与代码示例(超详细)
文章目录 前言1.队列的基本概念2.链表与数组实现队列的区别2.1数据存储结构2.2性能2.3内存使用 3.为什么选择链表实现队列?4.结构定义函数声明 5.核心操作5.1初始化 (QInit)5.2销毁 (QDestroy)5.3入队 (QPush)5.4出队 (QPop) 6.队列的查询操作6.1队首元素 (QueueFro…...
爬虫工作量由小到大的思维转变---<第二十三章 Scrapy开始很快,越来越慢(医病篇)>
诊断篇https://blog.csdn.net/m0_56758840/article/details/135170994?ops_request_misc%257B%2522request%255Fid%2522%253A%2522170333243316800180644102%2522%252C%2522scm%2522%253A%252220140713.130102334.pc%255Fall.%2522%257D&request_id1703332433168001806441…...
.Net7.0 或更高版本 System.Drawing.Common 上传图片跨平台方案
项目升级.Net7.0以后,System.Drawing.Common开关已经被删除,且System.Drawing.Common仅在 Windows 上支持 ,于是想办法将原来上传图片验证文件名和获取图片扩展名方法替换一下,便开始搜索相关解决方案。 .Net6.0文档:…...

【MySQL】InnoDB和MyISAM区别
文章目录 一、索引不同1 InnoDB聚簇索引,MyISAM非聚簇索引1 InnoDB聚簇索引2 MyISAM非聚簇索引 2 InnoDB必须要有主键,MyISAM允许没有主键3 InnoDB支持外键4 InnoDB不支持全文索引5 索引保存位置不同 二、对事物的支持三、存储结构不同四、存储空间不同五…...

3分钟了解安全数据交换系统有什么用!
企业为了保护核心数据安全,都会采取一些措施,比如做网络隔离划分,分成了不同的安全级别网络,或者安全域,接下来就是需要建设跨网络、跨安全域的安全数据交换系统,将安全保障与数据交换功能有机整合在一起&a…...
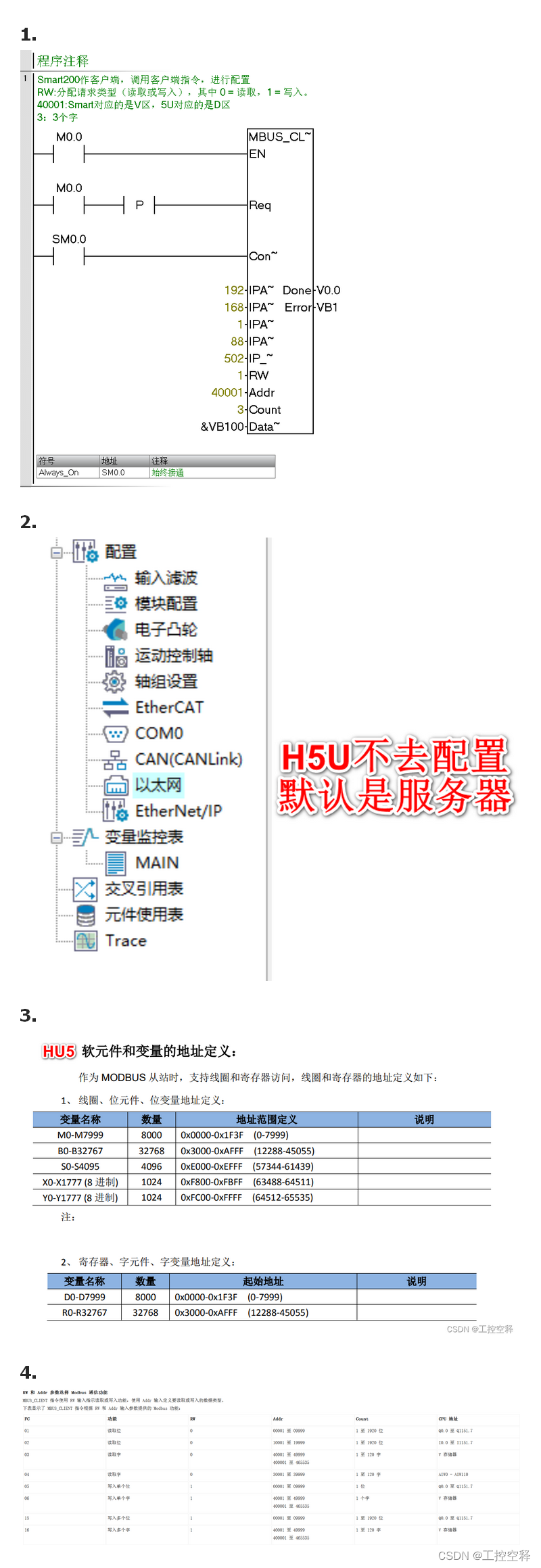
记录汇川:MODBUS TCP-梯形图
H5U的MODBUS通信不需要编写程序,通过组态MODBUS通信配置表,实现数据通信。 Modbus-TCP 主站即Modbus-TCP客户端,通过Modbus-TCP配置,可最多支持同时与31个 Modbus-TCP服务器(从站)进行通讯。 …...

electron + sqlite3 解决打包后无法写入数据库
前言 window环境。 electron28.0.0 sqlite35.1.6 使用 electron-builder 打包。 本文旨在解决打包后无法写入数据库的问题。 但如果你是打包后无法访问sqlite,且有报错弹窗,不妨也看看本文。 也许是同一种原因。 错误原因分析 打包后无法创建db文件&…...

【uniapp小程序-生成二维码+多个图片文字合并一张图】
<!-- 二维码 --><canvas id"qrcode" canvas-id"qrcode" width"120" ></canvas><!-- 生成带小程序码的分享图片 --><canvas canvas-id"shareCanvas" class"share-canvas"></canvas>#qrc…...
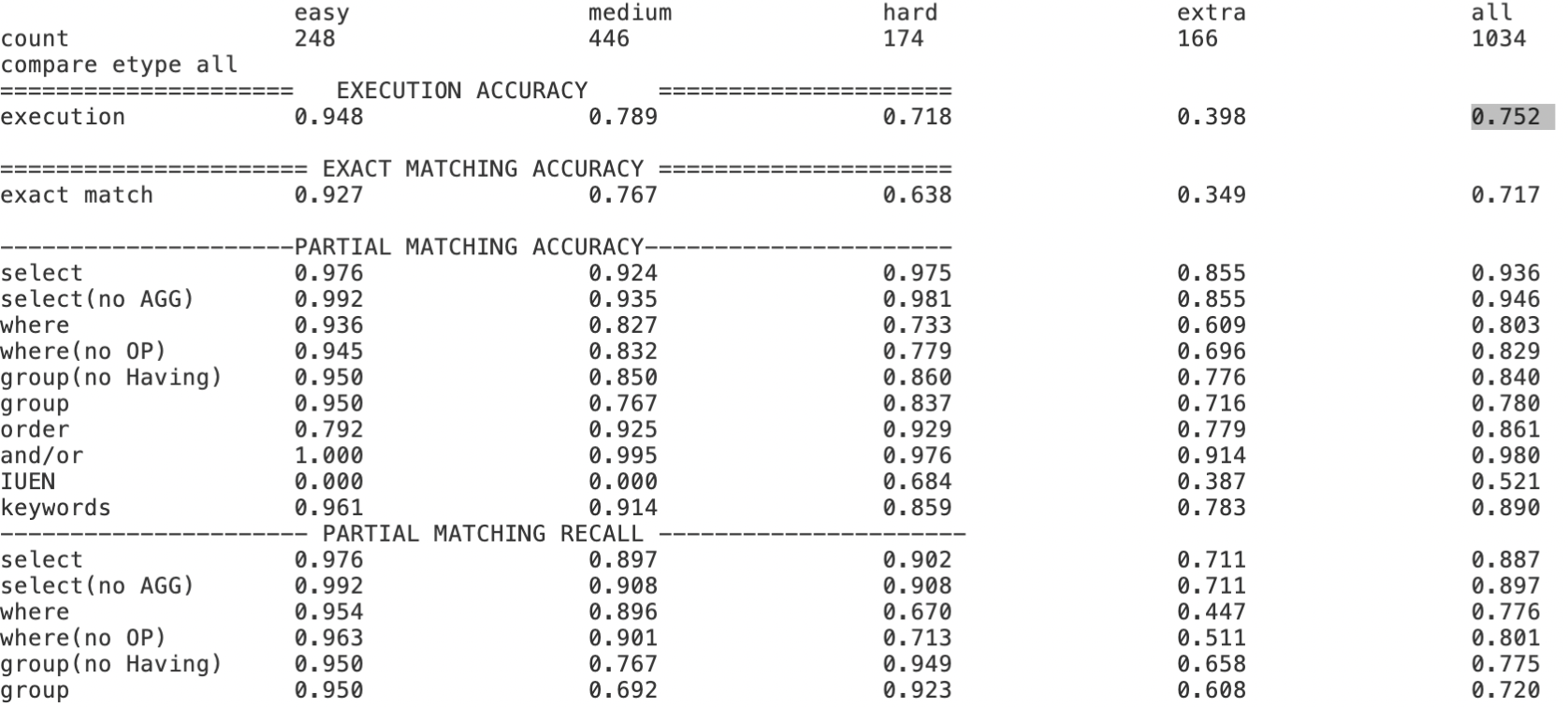
Text-to-SQL小白入门(十)RLHF在Text2SQL领域的探索实践
本文内容主要基于以下开源项目探索实践, Awesome-Text2SQL:GitHub - eosphoros-ai/Awesome-Text2SQL: Curated tutorials and resources for Large Language Models, Text2SQL, Text2DSL、Text2API、Text2Vis and more.DB-GPT-Hub:GitHub - eosphoros-ai…...
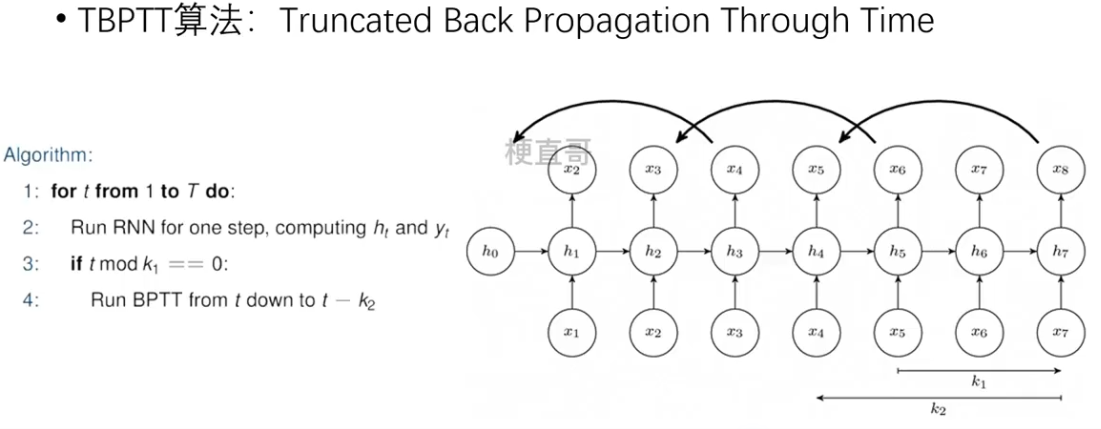
深度学习 | 基本循环神经网络
1、序列建模 1.1、序列数据 序列数据 —— 时间 不同时间上收集到的数据,描述现象随时间变化的情况。 序列数据 —— 文本 由一串有序的文本组成的序列,需要进行分词。 序列数据 —— 图像 有序图像组成的序列,后一帧图像可能会受前一帧的影响…...

VSCode 加Cortex-Debug嵌入式调试方法
简介 当使用ARM Cortex-M微控制器时,Cortex-Debug是一个Visual Studio Code的扩展,以简化调试过程。本文档介绍了如何编写启动配置(launch.json)。 settings.json配置 打开VSCode用户设置文件settings.json: 文件→偏好→设置选择用户设置: 在搜索栏中…...
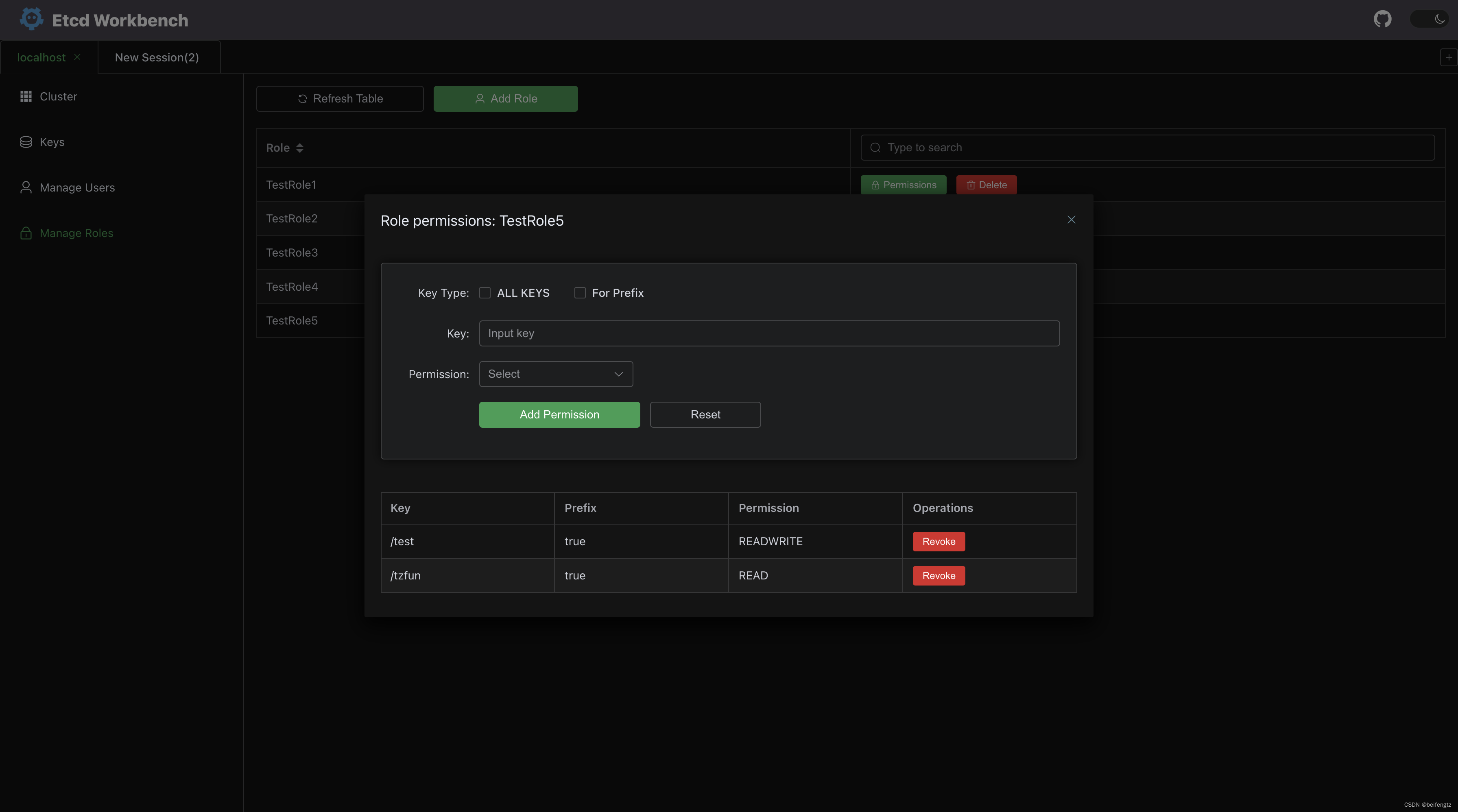
etcd-workbench一款免费好用的ETCD客户端,支持SSHTunnel、版本对比等功能
介绍 今天推荐一款完全免费的ETCD客户端,可以私有化部署: etcd-workbench 开源地址:https://github.com/tzfun/etcd-workbench Gitee地址:https://gitee.com/tzfun/etcd-workbench 下载 本地运行 从 官方Release 下载最新版的 jar 包&am…...

华为ipv6配置之ospf案例
R1 ipv6 ospfv3 1 router-id 1.1.1.1 //必须要手动配置ospf id,它不会自动生成 interface GigabitEthernet0/0/0 ipv6 enable ipv6 address 2000::2/96 ospfv3 1 area 0.0.0.0 interface LoopBack0 ipv6 enable ipv6 address 2001::1/96 ospfv3 1 area 0.0.0.0 R2…...

Design patterns--装饰模式
设计模式之装饰模式 使用装饰模式来封装Nmea0183语句。 代码 #ifndef DATAPARSER_H #define DATAPARSER_H#include <string> #include <vector>class DataParser { public:DataParser();virtual std::string fieldAnalysis(std::vector<std::string> vecSt…...
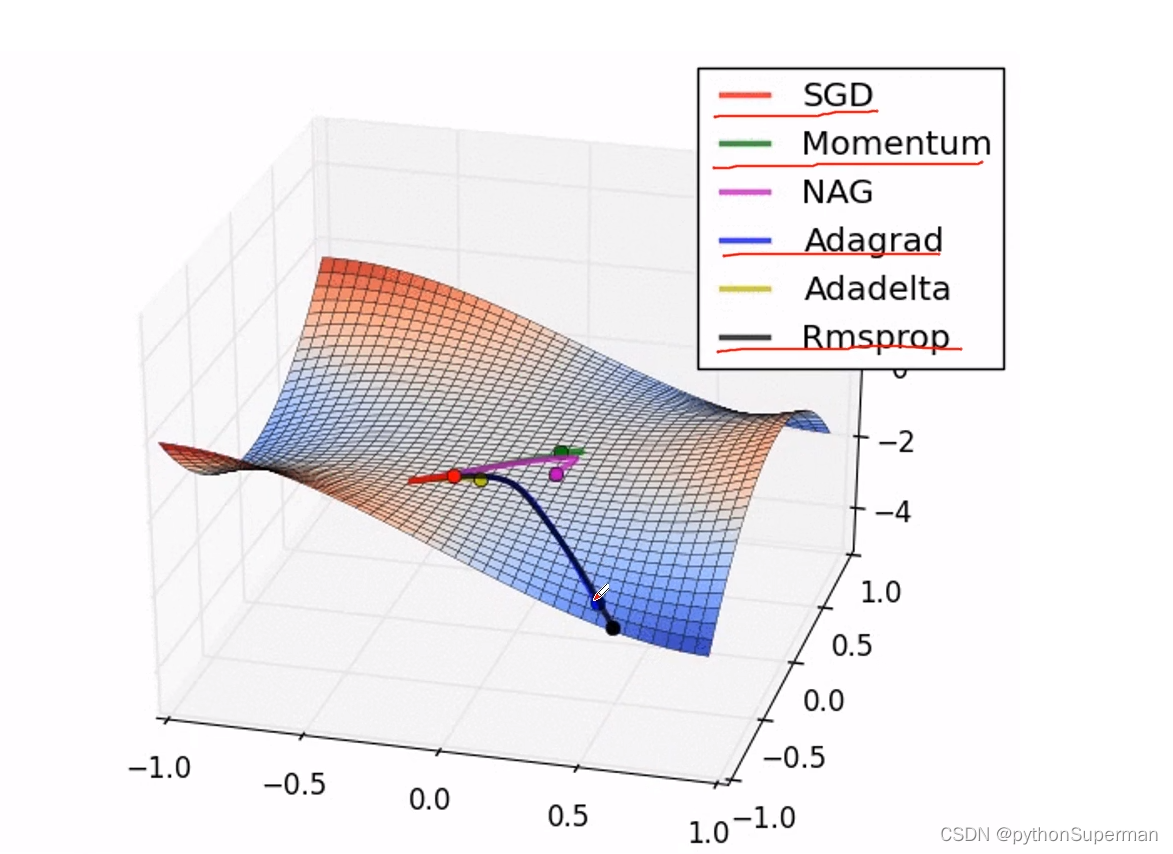
卷积神经网络 反向传播
误差的计算 softmax 经过softmax处理后所有输出节点概率和为1 损失(激活函数) 多分类问题:输出只可能归于某一个类别,不可能同时归于多个类别。 误差的反向传播 求w的误差梯度 权值的更新...

java面试题20
Java中的类加载机制可继续通过自定义类加载器来实现热部署、插件化和动态加载等功能,使得应用程序能够在运行时加载未知的类和资源。 什么是Java中的多线程(Multithreading)?它有什么作用? 答案:多线程是一…...
详解)
后进先出(LIFO)详解
LIFO 是 Last In, First Out 的缩写,中文译为后进先出。这是一种数据结构的工作原则,类似于一摞盘子或一叠书本: 最后放进去的元素最先出来 -想象往筒状容器里放盘子: (1)你放进的最后一个盘子(…...

业务系统对接大模型的基础方案:架构设计与关键步骤
业务系统对接大模型:架构设计与关键步骤 在当今数字化转型的浪潮中,大语言模型(LLM)已成为企业提升业务效率和创新能力的关键技术之一。将大模型集成到业务系统中,不仅可以优化用户体验,还能为业务决策提供…...
: K8s 核心概念白话解读(上):Pod 和 Deployment 究竟是什么?)
云原生核心技术 (7/12): K8s 核心概念白话解读(上):Pod 和 Deployment 究竟是什么?
大家好,欢迎来到《云原生核心技术》系列的第七篇! 在上一篇,我们成功地使用 Minikube 或 kind 在自己的电脑上搭建起了一个迷你但功能完备的 Kubernetes 集群。现在,我们就像一个拥有了一块崭新数字土地的农场主,是时…...

基于FPGA的PID算法学习———实现PID比例控制算法
基于FPGA的PID算法学习 前言一、PID算法分析二、PID仿真分析1. PID代码2.PI代码3.P代码4.顶层5.测试文件6.仿真波形 总结 前言 学习内容:参考网站: PID算法控制 PID即:Proportional(比例)、Integral(积分&…...

【人工智能】神经网络的优化器optimizer(二):Adagrad自适应学习率优化器
一.自适应梯度算法Adagrad概述 Adagrad(Adaptive Gradient Algorithm)是一种自适应学习率的优化算法,由Duchi等人在2011年提出。其核心思想是针对不同参数自动调整学习率,适合处理稀疏数据和不同参数梯度差异较大的场景。Adagrad通…...

深入解析C++中的extern关键字:跨文件共享变量与函数的终极指南
🚀 C extern 关键字深度解析:跨文件编程的终极指南 📅 更新时间:2025年6月5日 🏷️ 标签:C | extern关键字 | 多文件编程 | 链接与声明 | 现代C 文章目录 前言🔥一、extern 是什么?&…...

AI,如何重构理解、匹配与决策?
AI 时代,我们如何理解消费? 作者|王彬 封面|Unplash 人们通过信息理解世界。 曾几何时,PC 与移动互联网重塑了人们的购物路径:信息变得唾手可得,商品决策变得高度依赖内容。 但 AI 时代的来…...

算法:模拟
1.替换所有的问号 1576. 替换所有的问号 - 力扣(LeetCode) 遍历字符串:通过外层循环逐一检查每个字符。遇到 ? 时处理: 内层循环遍历小写字母(a 到 z)。对每个字母检查是否满足: 与…...

vulnyx Blogger writeup
信息收集 arp-scan nmap 获取userFlag 上web看看 一个默认的页面,gobuster扫一下目录 可以看到扫出的目录中得到了一个有价值的目录/wordpress,说明目标所使用的cms是wordpress,访问http://192.168.43.213/wordpress/然后查看源码能看到 这…...

莫兰迪高级灰总结计划简约商务通用PPT模版
莫兰迪高级灰总结计划简约商务通用PPT模版,莫兰迪调色板清新简约工作汇报PPT模版,莫兰迪时尚风极简设计PPT模版,大学生毕业论文答辩PPT模版,莫兰迪配色总结计划简约商务通用PPT模版,莫兰迪商务汇报PPT模版,…...
