复试 || 就业day01(2023.12.27)算法篇
文章目录
- 前言
- 两数之和
- 存在重复元素 II
- 好数对的数目
- 总持续时间可被 60 整除的歌曲
前言
💫你好,我是辰chen,本文旨在准备考研复试或就业
💫文章题目大多来自于 leetcode,当然也可能来自洛谷或其他刷题平台
💫欢迎大家的关注,我的博客主要关注于考研408以及AIoT的内容
🌟 仅给出C++版代码
以下的几个专栏是本人比较满意的专栏(大部分专栏仍在持续更新),欢迎大家的关注:
💥ACM-ICPC算法汇总【基础篇】
💥ACM-ICPC算法汇总【提高篇】
💥AIoT(人工智能+物联网)
💥考研
💥CSP认证考试历年题解
两数之和
题目链接:两数之和
C++版AC代码:
暴力:时间复杂度 O ( n 2 ) O(n^2) O(n2),空间复杂度 O ( 1 ) O(1) O(1)
class Solution {
public:vector<int> twoSum(vector<int>& nums, int target) {int n = nums.size();for (int i = 0; i < n; i ++ )for (int j = i + 1; j < n; j ++ ){if (nums[i] + nums[j] == target){return {i, j};}}return {};}
};
哈希:时间复杂度 O ( n ) O(n) O(n)【 find 的时间复杂度为 O ( 1 ) O(1) O(1)】,空间复杂度 O ( n ) O(n) O(n)【建立了一个空哈希表】
注意因为 find 查的是 first 所以我们在插入的时候,first = nums[i],second = i
class Solution {
public:vector<int> twoSum(vector<int>& nums, int target) {int n = nums.size();unordered_map<int, int> m;for (int i = 0; i < n; i ++ ) {auto it = m.find(target - nums[i]);if (it != m. end()){return {it -> second, i};}m[nums[i]] = i;}return {};}
};
存在重复元素 II
题目链接:存在重复元素 II
C++版AC代码:
同样是使用哈希表,这里需要注意,哈希的插入是直接使用 m[nums[i]] = i; 不可以使用 m.insert(make_pair(nums[i], i)),因为nums中是会有相同的值重复出现的,我们只需要保存距离最近的一个点就可以了,但是 insert 操作只会保存第一个存入的键值对,后续相同的键值不会更新
class Solution {
public:bool containsNearbyDuplicate(vector<int>& nums, int k) {unordered_map<int, int> m;for (int i = 0; i < nums.size(); i ++ ) {auto it = m.find(nums[i]);if (it != m.end() && abs(m[nums[i]] - i) <= k) return true;m[nums[i]] = i;}return false;}
};
好数对的数目
题目链接:好数对的数目
C++版AC代码:
桶的思想
class Solution {
public:int numIdenticalPairs(vector<int>& nums) {int cnt = 0;int t[110] = {0};for (int i = 0; i < nums.size(); i ++ ){cnt += t[nums[i]];t[nums[i]] ++;}return cnt;}
};
C++版AC代码:
哈希也可,本质无区别
class Solution {
public:int numIdenticalPairs(vector<int>& nums) {int cnt = 0;unordered_map<int, int> m;for (int i = 0; i < nums.size(); i ++ ){cnt += m[nums[i]];m[nums[i]] ++;}return cnt;}
};
总持续时间可被 60 整除的歌曲
题目链接:总持续时间可被 60 整除的歌曲
C++版AC代码:
哈希维护出现的次数,依次枚举可能的解,因为元素的大小为 [1, 500],故 j 的上限为 1000,每次 +60
class Solution {
public:int numPairsDivisibleBy60(vector<int>& time) {unordered_map<int, int> m;int cnt = 0;for (int i = 0; i < time.size(); i ++ ){for (int j = 60; j < 1000; j += 60 ){int tmp = j - time[i];auto it = m.find(tmp);if (it != m.end()) cnt += m[tmp];}m[time[i]] ++;}return cnt;}
};
C++版AC代码:
其实是没必要进行枚举的,开一个大小为 60 的数组,找可以被 60 整除的另一个数实际上就是在找 60 - time[i] % 60,特别的对于自身就可以被 60 整除的数,需要将其映射回 0,故对于每一个 time[i],去找 (60 - time[i] % 60) % 60
class Solution {
public:int numPairsDivisibleBy60(vector<int>& time) {int cnt = 0;int nums[65] = {0};for (int i = 0; i < time.size(); i ++ ){cnt += nums[(60 - time[i] % 60) % 60];nums[time[i] % 60] ++;}return cnt;}
};
相关文章:
算法篇)
复试 || 就业day01(2023.12.27)算法篇
文章目录 前言两数之和存在重复元素 II好数对的数目总持续时间可被 60 整除的歌曲 前言 💫你好,我是辰chen,本文旨在准备考研复试或就业 💫文章题目大多来自于 leetcode,当然也可能来自洛谷或其他刷题平台 Ὂ…...
JavaWeb——JQuery
文章目录 JQuery 是什么?jQuery 的原理示意图JQuery 基本开发步骤jQuery 对象和 DOM 对象将dom对象转为JQuery对象jQuery 对象转成 DOM 对象jQuery 选择器基本选择器基础过滤选择器JQuery 是什么? 基本介绍 jQuery 是一个快速的,简洁的 javaScript 库,使用户能更方便地处理…...

Python教程:查询Py模块的版本号,有哪些方法?
1.查看模块内部的版本信息:如果你已经导入了该模块,可以查看模块内部的__version__属性来获取版本信息。例如,对于pandas模块,可以运行import pandas和print(pandas.version)来获取版本信息。 import pandas print(pandas.__vers…...
第一节 初始化项目
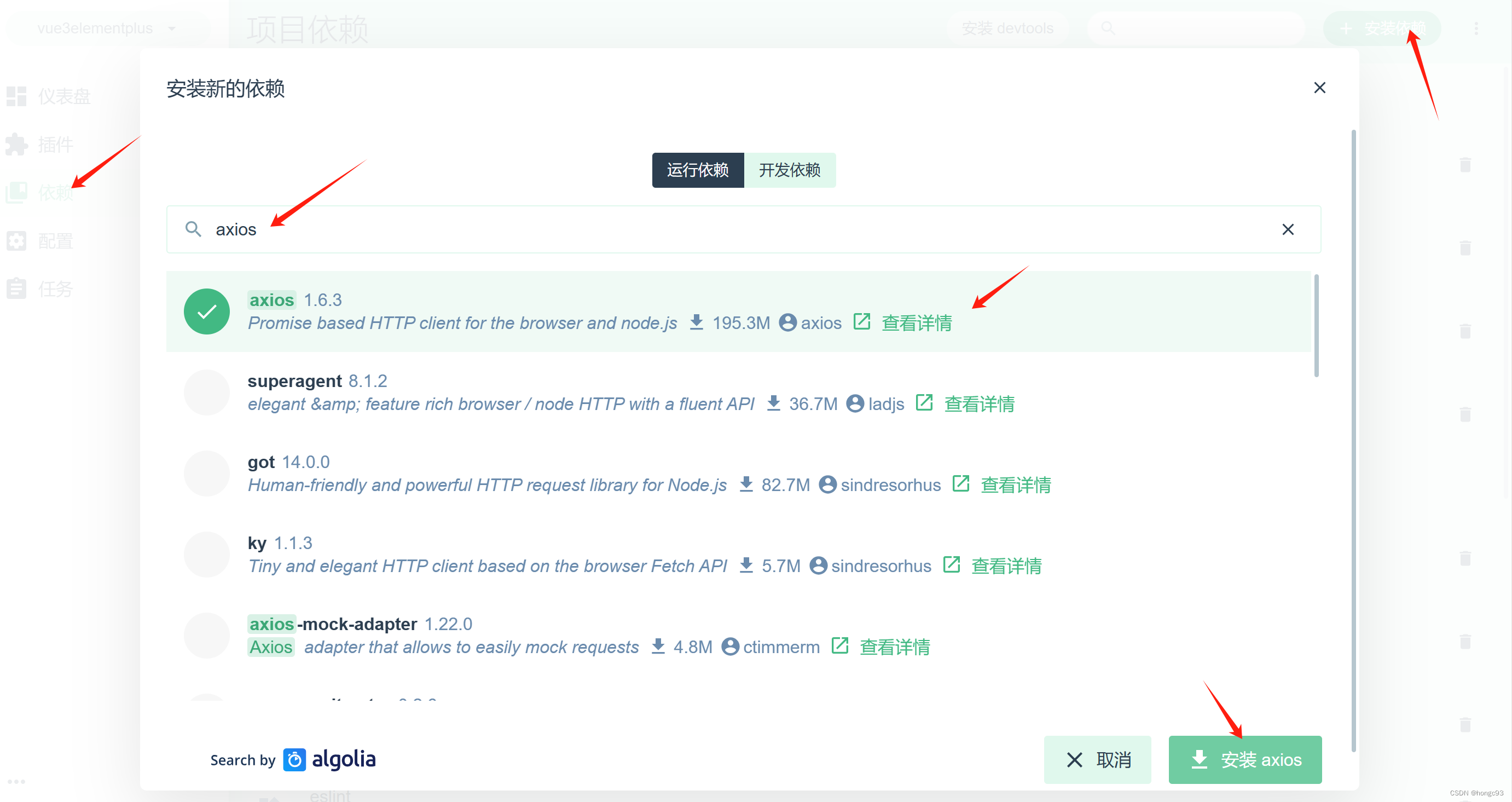
系列文章目录 第一节 初始化项目 文章目录 操作步骤 总结 操作步骤 打开cmd 输入 vue ui 在打开的网页中点击“创建”,复制文件夹路径并粘贴点击“在此创建新项目” 输入项目名称 点击下一步选择手动配置 选择babel、router、vuex、css pre-processors、 linter建…...
idea提示unable to import maven project
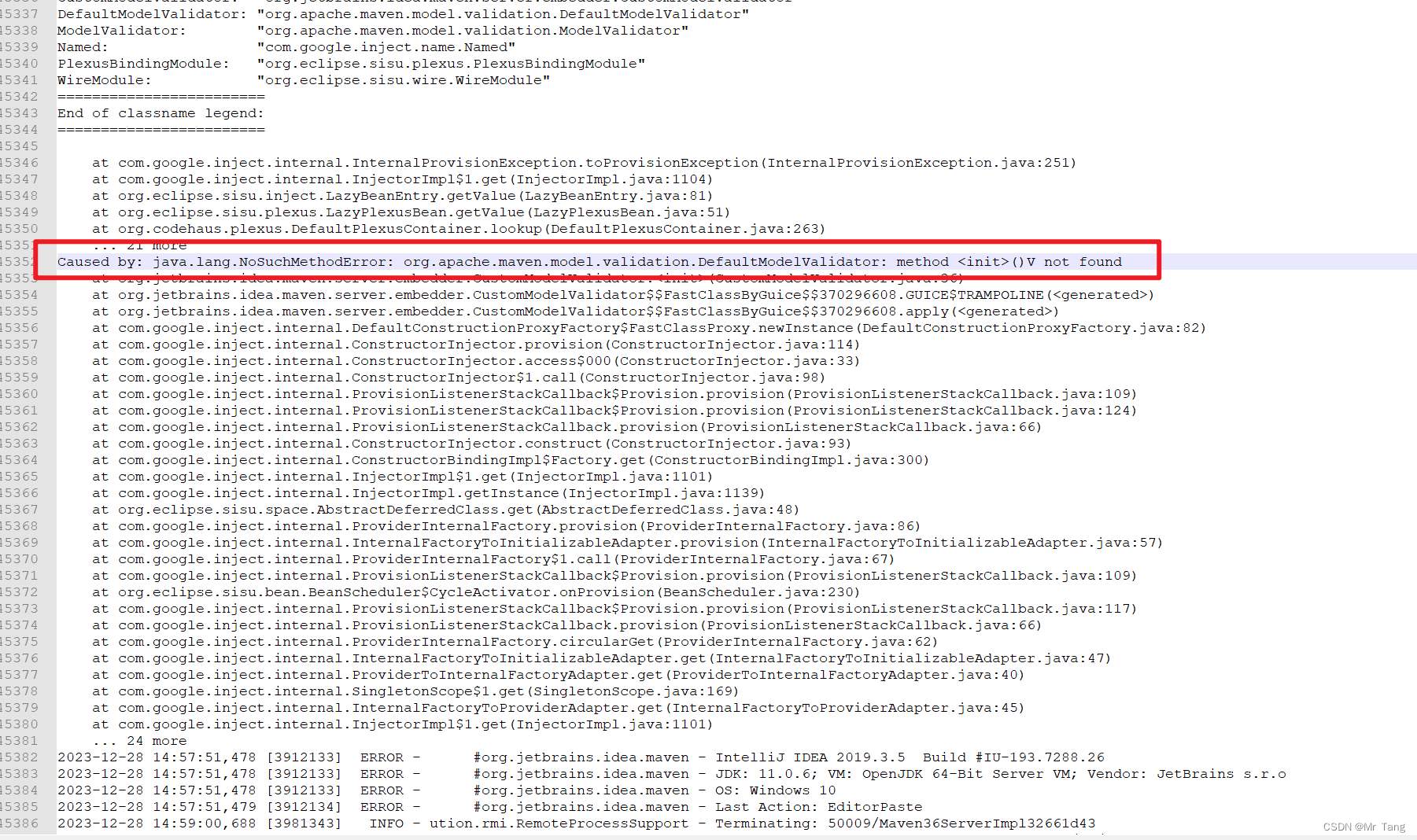
问题描述: idea导入maven依赖时提示unable to import maven project 打开log日志如下: 问题原因以及解决方案: maven版本与idea版本不兼容,切换maven版本即可...

【Spring】SpringBoot日志
文章目录 什么是日志日志的用途日志的使用如何打印日志日志级别日志框架门面模式(外观模式)日志级别的使用配置日志级别日志持久化配置日志的存储目录配置日志文件名配置日志文件分割 更简单的日志输出 什么是日志 在计算机领域,日志是一个记…...

HTML+CSS制作动漫绿巨人
🎀效果展示 🎀代码展示 <!DOCTYPE html> <html lang="en" > <head>...

AGV智能搬运机器人-替代人工工位让物流行业降本增效
在当今快速发展的世界中,物流业面临着巨大的挑战,包括提高效率、降低成本和优化工作流程。为了应对这些挑战,一种新型的自动化设备——智能搬运机器人正在崭露头角。本文将通过一个具体的案例来展示富唯智能转运机器人在实际应用中的价值。 案…...
【办公技巧】怎么批量提取文件名到excel
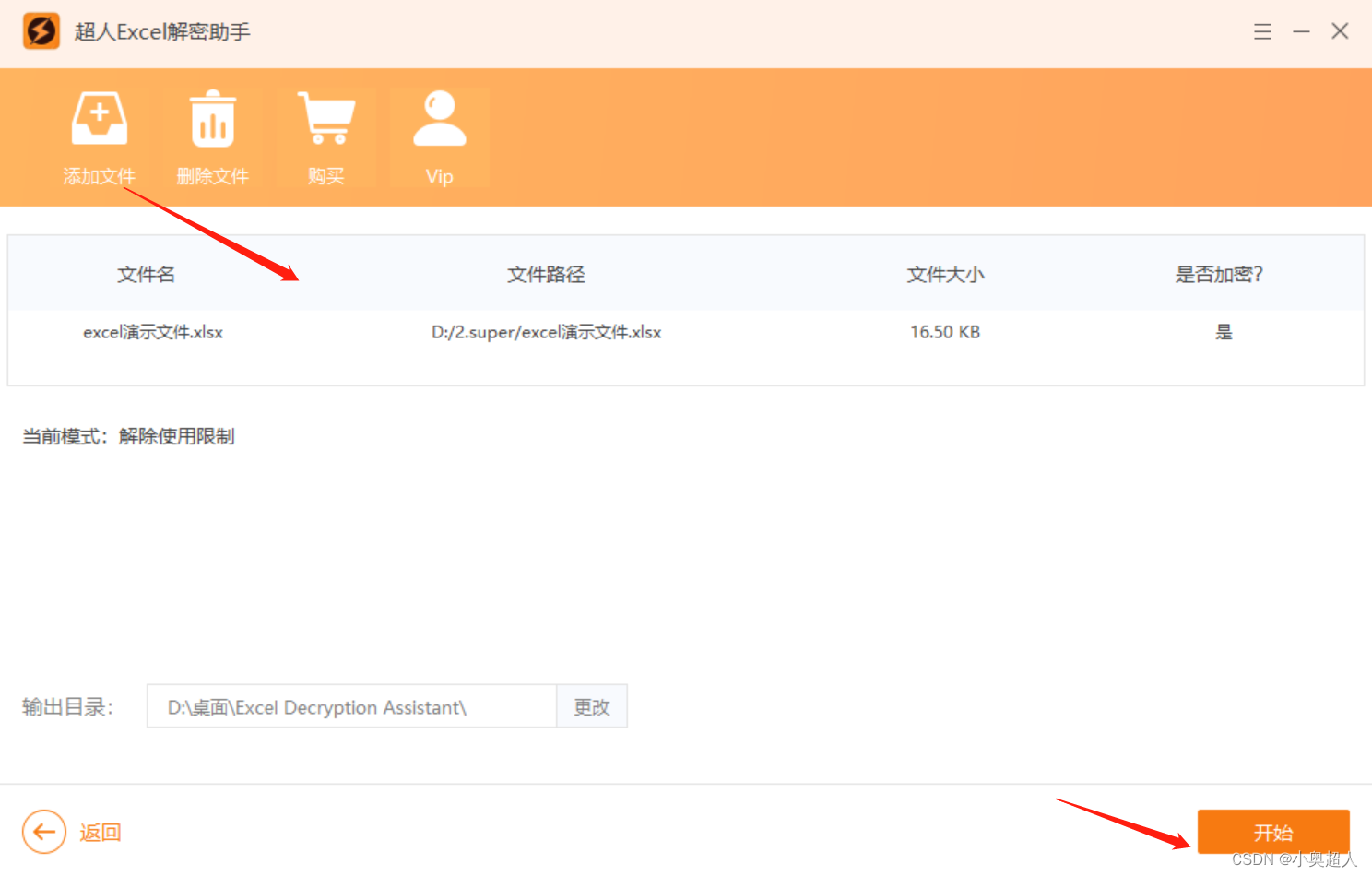
Excel是大家经常用来制作表格的文件,比如输入文件名,如果有大量文件需要输入,用张贴复制或者手动输入的方式还是很费时间的,今天和大家分享如何批量提取文件名。 打开需要提取文件名的文件夹,选中所有文件,…...

uniapp实现前端银行卡隐藏中间的数字,及隐藏姓名后两位
Vue 实现前端银行卡隐藏中间的数字 主要应用了 filters过滤器 来实现效果 实现效果,如图: <template><div><div style"background-color: #f4f4f4;margin:50px 0 0 460px;width:900px;height:300px;"><p>原来&#…...

HPCC:高精度拥塞控制
HPCC:高精度拥塞控制 文章目录 HPCC:高精度拥塞控制摘要1 引言1.1 背景1.2 现有CC的局限性1.3 HPCC的提出 2 研究动机2.1 大型RDMA部署2.2 RDMA目标2.3 当前RDMA CC中的权衡DCQCNTIMELY 2.4 下一代高速CC 3 技术方案3.1 INT3.2 HPCC设计3.3 HPPC的参数 4…...

centos 配置 git 连接 github
centos 配置 git 连接 github 首先安装 git 创建 ssh key ssh-keygen -t rsa复制公钥 cat ~/.ssh/id_rsa.pub # 打印出公钥内容然后复制配置 github 登录网页 github 账号;进入 setting;点击 SSH and GPG keys,点击 New SSH keytitile 随便填…...
SpringBoot发布项目到docker
Dockerfile FROM openjdk:11 # 作者 MAINTAINER chenxiaodong<2774398338qq.com># 安装 vim # RUN yum -y install vim# 环境变量 # 进入容器后的默认工作目录 ENV WORKPATH /usr/local/webapp ENV EXECFILE Docker2Application-0.0.1-SNAPSHOT.jarRUN mkdir -p $WORKPA…...
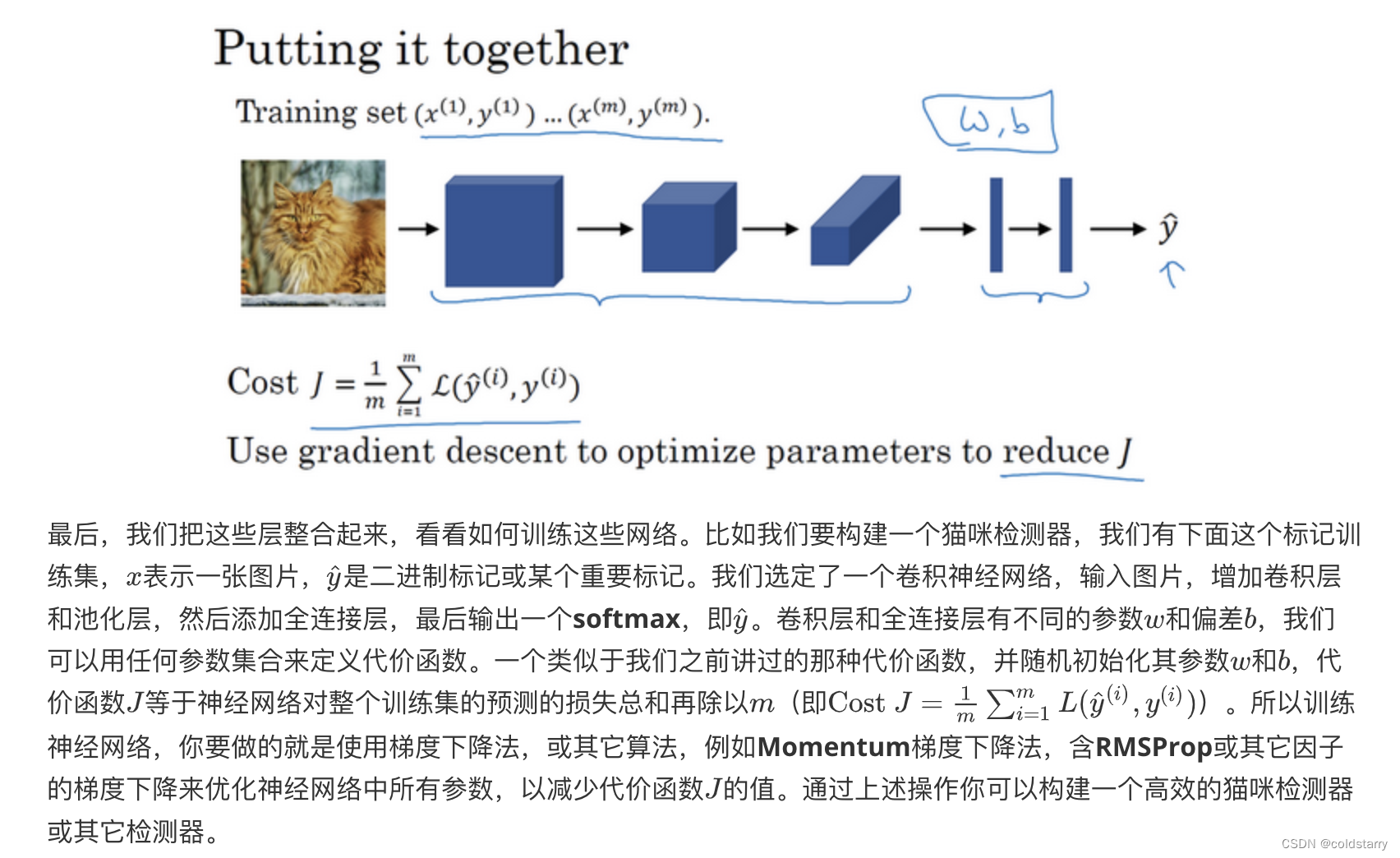
sheng的学习笔记-卷积神经网络
源自吴恩达的深度学习课程,仅用于笔记,便于自行复习 导论 1)什么是卷积神经网络 卷积神经网络,也就是convolutional neural networks (简称CNN),使用卷积算法的神经网络,常用于计…...
)
数据库:园林题库软件(《中国古代园林史》答题卷一 )
《中国古代园林史》答题卷一 填空题 1、中国古代园林曾被誉为“世界园林之母”。国际风景园林师联合会(IFLA)的创始人、著名风景园林师和教育家杰里柯爵士( Sir Geoffrey Alan Jellicoe)把中国古代园林和西亚园林以及古希腊园林列为世界三大园林体系之首。 2、中国古代园林是…...
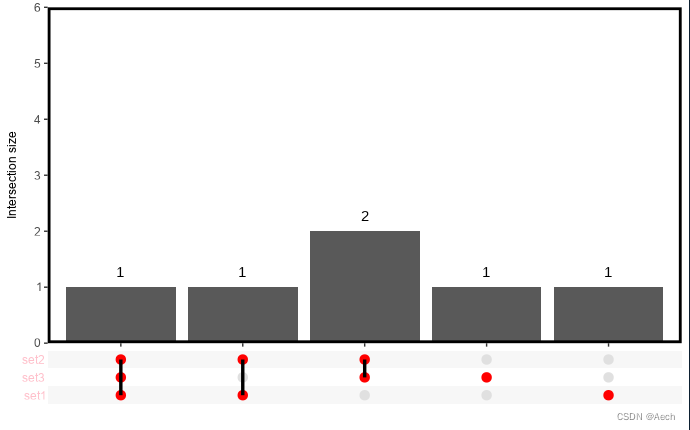
upset 绘制
好久没有更新,今天来一个upset图的绘制 1.1 安装包 #绘制upset的包现在看来有三个 ## UpSet ### 最基本的upsetR包,使用方便,但是扩展不方便 devtools::install_github("hms-dbmi/UpSetR") ## complex-upset ### UpSet的升级款 支持ggplot2 devtools::install_git…...
声明 | 为打击假冒账号、恶意抄袭账号等诈骗活动,提升本账号权威,本博主特此郑重声明
声明 | 为打击假冒账号、恶意抄袭账号诈骗活动,提升本账号权威,本博主特此郑重声明 一、本账号为《机器学习之心》博主CSDN唯一官方账号,唯一联系方式见文章底部。 二、《机器学习之心》博主未授权任何第三方账号进行模型合作、程序设计、源…...

云计算:OpenStack 配置二层物理网卡为三层桥的接口
目录 一、理论 1.OpenStack 二、实验 1. Linux系统修改网卡 2.OpenStack 配置二层物理网卡为三层桥的接口 一、理论 1.OpenStack (1)概念 OpenStack是一个开源的云计算管理平台项目,是一系列软件开源项目的组合。由NASA(美国国家航空…...

Python sanic框架钉钉和第三方打卡机实现
同样还是需要开通钉钉应用这里就不错多说了 第一步:梳理逻辑流程 前提:打卡的机器是使用postgres数据库,由于因为某些原因,钉钉userId 我已经提前获取到了存放到数据库里。 1.用户打卡成功后,我们应该监听数据库进行查询…...

微信小程序性能优化
1. 代码包不包含插件大小超过 1.5 M 建议:小程序代码包单个包大小限制为2M。因此我们建议开发者在开发时,如果遇到单包体积大于1.5M的情况,可以采取分包的方式,把部分代码拆分到分包去,降低单个包的体积,提…...

浅谈 React Hooks
React Hooks 是 React 16.8 引入的一组 API,用于在函数组件中使用 state 和其他 React 特性(例如生命周期方法、context 等)。Hooks 通过简洁的函数接口,解决了状态与 UI 的高度解耦,通过函数式编程范式实现更灵活 Rea…...

web vue 项目 Docker化部署
Web 项目 Docker 化部署详细教程 目录 Web 项目 Docker 化部署概述Dockerfile 详解 构建阶段生产阶段 构建和运行 Docker 镜像 1. Web 项目 Docker 化部署概述 Docker 化部署的主要步骤分为以下几个阶段: 构建阶段(Build Stage):…...

关于nvm与node.js
1 安装nvm 安装过程中手动修改 nvm的安装路径, 以及修改 通过nvm安装node后正在使用的node的存放目录【这句话可能难以理解,但接着往下看你就了然了】 2 修改nvm中settings.txt文件配置 nvm安装成功后,通常在该文件中会出现以下配置&…...

AtCoder 第409场初级竞赛 A~E题解
A Conflict 【题目链接】 原题链接:A - Conflict 【考点】 枚举 【题目大意】 找到是否有两人都想要的物品。 【解析】 遍历两端字符串,只有在同时为 o 时输出 Yes 并结束程序,否则输出 No。 【难度】 GESP三级 【代码参考】 #i…...

Leetcode 3577. Count the Number of Computer Unlocking Permutations
Leetcode 3577. Count the Number of Computer Unlocking Permutations 1. 解题思路2. 代码实现 题目链接:3577. Count the Number of Computer Unlocking Permutations 1. 解题思路 这一题其实就是一个脑筋急转弯,要想要能够将所有的电脑解锁&#x…...

Maven 概述、安装、配置、仓库、私服详解
目录 1、Maven 概述 1.1 Maven 的定义 1.2 Maven 解决的问题 1.3 Maven 的核心特性与优势 2、Maven 安装 2.1 下载 Maven 2.2 安装配置 Maven 2.3 测试安装 2.4 修改 Maven 本地仓库的默认路径 3、Maven 配置 3.1 配置本地仓库 3.2 配置 JDK 3.3 IDEA 配置本地 Ma…...

深度学习习题2
1.如果增加神经网络的宽度,精确度会增加到一个特定阈值后,便开始降低。造成这一现象的可能原因是什么? A、即使增加卷积核的数量,只有少部分的核会被用作预测 B、当卷积核数量增加时,神经网络的预测能力会降低 C、当卷…...

招商蛇口 | 执笔CID,启幕低密生活新境
作为中国城市生长的力量,招商蛇口以“美好生活承载者”为使命,深耕全球111座城市,以央企担当匠造时代理想人居。从深圳湾的开拓基因到西安高新CID的战略落子,招商蛇口始终与城市发展同频共振,以建筑诠释对土地与生活的…...
: 一刀斩断视频片头广告)
快刀集(1): 一刀斩断视频片头广告
一刀流:用一个简单脚本,秒杀视频片头广告,还你清爽观影体验。 1. 引子 作为一个爱生活、爱学习、爱收藏高清资源的老码农,平时写代码之余看看电影、补补片,是再正常不过的事。 电影嘛,要沉浸,…...

libfmt: 现代C++的格式化工具库介绍与酷炫功能
libfmt: 现代C的格式化工具库介绍与酷炫功能 libfmt 是一个开源的C格式化库,提供了高效、安全的文本格式化功能,是C20中引入的std::format的基础实现。它比传统的printf和iostream更安全、更灵活、性能更好。 基本介绍 主要特点 类型安全:…...
