数据挖掘 K-Means聚类
未格式化之前的代码:
import pandas as pd#数据处理
from matplotlib import pyplot as plt#绘图
from sklearn.preprocessing import MinMaxScaler#归一化
from sklearn.cluster import KMeans#聚类
import os#处理文件os.environ["OMP_NUM_THREADS"] = '4'df = pd.read_excel("consumption_data.xls", usecols=["R", "F", "M"])#选取了“R”、“F”和“M”三列数据
df.dropna(inplace=True)#将缺失值删除
df_scale = MinMaxScaler().fit_transform(df)#归一化,使得数据在0到1的范围内
model = KMeans(n_clusters=3, random_state=0)#n_clusters参数设置为3,表示要将数据分成3个簇。random_state参数设置为0,以确保每次运行时都得到相同的结果
model.fit(df_scale)#训练模型
core = model.cluster_centers_#通过cluster_centers_属性获取聚类模型中心点的坐标,即每个簇的中心点
df["class"] = model.labels_#将每个数据点的簇标签保存在原始数据集的“class”列中,使用labels_属性获取每个数据点所属的簇的标签fig = plt.figure(figsize=(9, 9))#创建一个大小为9x9的图形窗口
ax = plt.axes(projection='3d')#创建一个3D坐标轴
center_x = []#创建空列表用于存储各个簇的中心点坐标。
center_y = []
center_z = []
for i, j in df.groupby(by="class"):#对数据集按簇标签进行分组ax.scatter3D(j["F"], j["R"], j["M"], label=i)#将每个簇的数据点在3D空间中绘制为散点图center_x.append(j["F"].mean())#计算每个簇的中心点坐标,并将其添加到相应的列表中。center_y.append(j["R"].mean())center_z.append(j["M"].mean())# ax.scatter3D(j["F"].mean(),j["R"].mean(),j["M"].mean(),marker="X") 使用scatter3D()函数将每个簇的中心点坐标(j["F"].mean(), j["R"].mean(), j["M"].mean())以"X"形状的标记绘制在图中。
ax.scatter3D(center_x, center_y, center_z, label='center', marker="X", alpha=1)#以“X”形状的标记绘制簇的中心点。alpha参数设置为1,表示散点图的透明度为完全不透明
plt.legend()#显示图例
plt.show()#显示图形for i, j in df.groupby(by="class"):#对数据集按簇标签进行分组。j[["R", "F", "M"]].plot(kind="kde", subplots=True, sharex=False)#对每个簇的三个特征绘制核密度图。kind="kde"指定绘制核密度图,subplots=True表示将三个子图绘制在同一画布上,sharex=False表示不共享x轴。plt.subplots_adjust(hspace=0.3) # 调整子图的纵向间隙,hspace=0.3将纵向间隔设置为子图高度的30%。这将使得每个子图之间有一定的空白间隔plt.show()#显示图形
格式化之后的代码:
import pandas as pd # 数据处理
from matplotlib import pyplot as plt # 绘图
from sklearn.preprocessing import MinMaxScaler # 归一化
from sklearn.cluster import KMeans # 聚类
import os # 处理文件os.environ["OMP_NUM_THREADS"] = '4'df = pd.read_excel("consumption_data.xls", usecols=["R", "F", "M"]) # 选取了“R”、“F”和“M”三列数据
df.dropna(inplace=True) # 将缺失值删除
df_scale = MinMaxScaler().fit_transform(df) # 归一化,使得数据在0到1的范围内
model = KMeans(n_clusters=3, random_state=0) # n_clusters参数设置为3,表示要将数据分成3个簇。random_state参数设置为0,以确保每次运行时都得到相同的结果
model.fit(df_scale) # 训练模型
core = model.cluster_centers_ # 通过cluster_centers_属性获取聚类模型中心点的坐标,即每个簇的中心点
df["class"] = model.labels_ # 将每个数据点的簇标签保存在原始数据集的“class”列中,使用labels_属性获取每个数据点所属的簇的标签fig = plt.figure(figsize=(9, 9)) # 创建一个大小为9x9的图形窗口
ax = plt.axes(projection='3d') # 创建一个3D坐标轴
center_x = [] # 创建空列表用于存储各个簇的中心点坐标。
center_y = []
center_z = []
for i, j in df.groupby(by="class"): # 对数据集按簇标签进行分组ax.scatter3D(j["F"], j["R"], j["M"], label=i) # 将每个簇的数据点在3D空间中绘制为散点图center_x.append(j["F"].mean()) # 计算每个簇的中心点坐标,并将其添加到相应的列表中。center_y.append(j["R"].mean())center_z.append(j["M"].mean())# ax.scatter3D(j["F"].mean(),j["R"].mean(),j["M"].mean(),marker="X") 使用scatter3D()函数将每个簇的中心点坐标(j["F"].mean(), j["R"].mean(), j["M"].mean())以"X"形状的标记绘制在图中。
ax.scatter3D(center_x, center_y, center_z, label='center', marker="X",alpha=1) # 以“X”形状的标记绘制簇的中心点。alpha参数设置为1,表示散点图的透明度为完全不透明
plt.legend() # 显示图例
plt.show() # 显示图形for i, j in df.groupby(by="class"): # 对数据集按簇标签进行分组。j[["R", "F", "M"]].plot(kind="kde", subplots=True,sharex=False) # 对每个簇的三个特征绘制核密度图。kind="kde"指定绘制核密度图,subplots=True表示将三个子图绘制在同一画布上,sharex=False表示不共享x轴。plt.subplots_adjust(hspace=0.3) # 调整子图的纵向间隙,hspace=0.3将纵向间隔设置为子图高度的30%。这将使得每个子图之间有一定的空白间隔plt.show() # 显示图形
相关文章:

数据挖掘 K-Means聚类
未格式化之前的代码: import pandas as pd#数据处理 from matplotlib import pyplot as plt#绘图 from sklearn.preprocessing import MinMaxScaler#归一化 from sklearn.cluster import KMeans#聚类 import os#处理文件os.environ["OMP_NUM_THREADS"] …...

医疗卫生行业网络安全需求发展
文章目录 一、行业安全建设需求分析1、等级保护2.0合规建设云计算技术大数据技术物联网技术移动互联网技术2、加强医疗数据安全保护加密存储与传输数据加强数据备份与恢复注重数据脱敏与分级保护3、强化网络安全制度管理完善应急预案与响应机制加强网络安全人员管理二、行业新技…...

【Unity热更新】学会AssetsBundle打包、加载、卸载
本教程详细讲解什么是AssetBundle压缩包机制!然后构建 AssetBundle、加载 AssetBundle 以及卸载 AssetBundle 的简要教程。这一个流程就是热更新! AssetBundles 简介 1.什么是AssetBundles? AssetBundles是Unity中一种用于打包和存储资源(如模型、纹理、声音等)的文件格…...

智能优化算法应用:基于指数分布算法3D无线传感器网络(WSN)覆盖优化 - 附代码
智能优化算法应用:基于指数分布算法3D无线传感器网络(WSN)覆盖优化 - 附代码 文章目录 智能优化算法应用:基于指数分布算法3D无线传感器网络(WSN)覆盖优化 - 附代码1.无线传感网络节点模型2.覆盖数学模型及分析3.指数分布算法4.实验参数设定5.算法结果6.…...

vue 监听浏览器关闭或刷新事件
vue 监听浏览器关闭或刷新事件 需求 web项目中使用socket时,涉及到关闭刷新浏览器多次连接问题,其中一个解决方法是在关闭或刷新浏览器时,将连接断开。 代码 <script> export default {// 可以在created、beforeMount或mounted生命…...

VuePress-theme-hope 搭建个人博客 2【快速上手】 —— 安装、部署 防止踩坑篇
续👆VuePress、VuePress-theme-hope 搭建个人博客 1【快速上手】 项目常用命令 vuepress dev [dir] 会启动一个开发服务器,以便让你在本地开发你的 VuePress 站点。vuepress build [dir] 会将你的 VuePress 站点构建成静态文件,以便你进行后…...
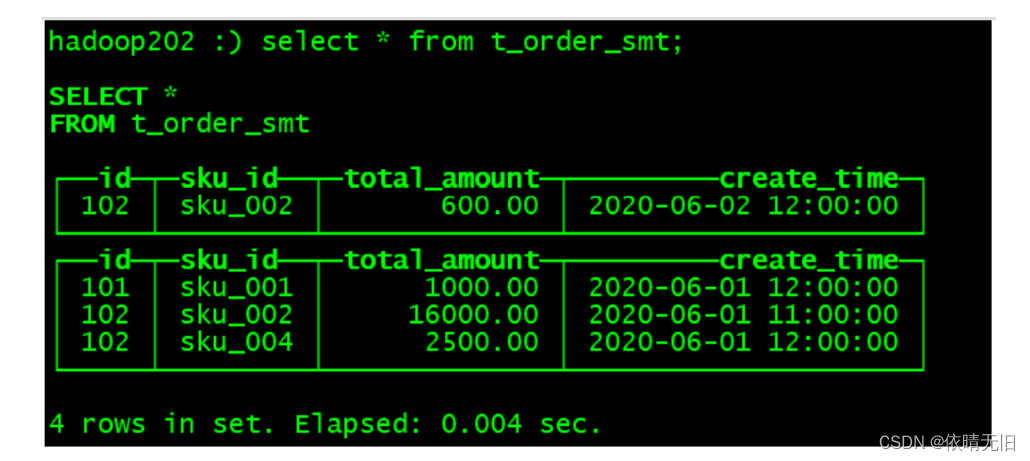
ClickHouse基础知识(四):ClickHouse 引擎详解
1. 表引擎的使用 表引擎是 ClickHouse 的一大特色。可以说, 表引擎决定了如何存储表的数据。包括: ➢ 数据的存储方式和位置,写到哪里以及从哪里读取数据。 默认存放在/var/lib/clickhouse/data ➢ 支持哪些查询以及如何支持。 ➢ 并发数…...
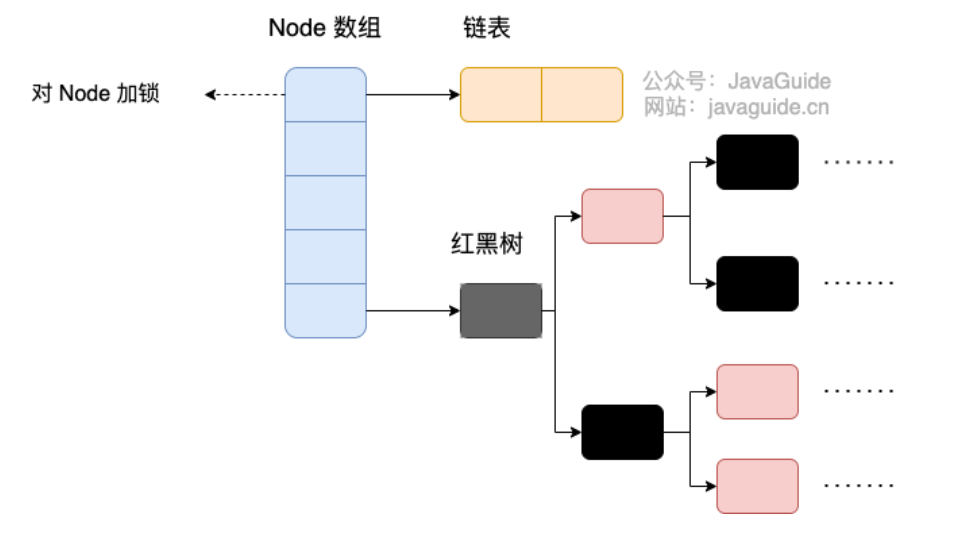
关于设计模式、Java基础面试题
前言 之前为了准备面试,收集整理了一些面试题。 本篇文章更新时间2023年12月27日。 最新的内容可以看我的原文:https://www.yuque.com/wfzx/ninzck/cbf0cxkrr6s1kniv 设计模式 单例共有几种写法? 细分起来就有9种:懒汉&#x…...

Python爱心光波完整代码
文章目录 环境需求完整代码详细分析环境需求 python3.11.4PyCharm Community Edition 2023.2.5pyinstaller6.2.0(可选,这个库用于打包,使程序没有python环境也可以运行,如果想发给好朋友的话需要这个库哦~)【注】 python环境搭建请见:https://want595.blog.csdn.net/arti…...

PowerShell Instal 一键部署gitea
gitea 前言 Gitea 是一个轻量级的 DevOps 平台软件。从开发计划到产品成型的整个软件生命周期,他都能够高效而轻松的帮助团队和开发者。包括 Git 托管、代码审查、团队协作、软件包注册和 CI/CD。它与 GitHub、Bitbucket 和 GitLab 等比较类似。 Gitea 最初是从 Gogs 分支而来…...
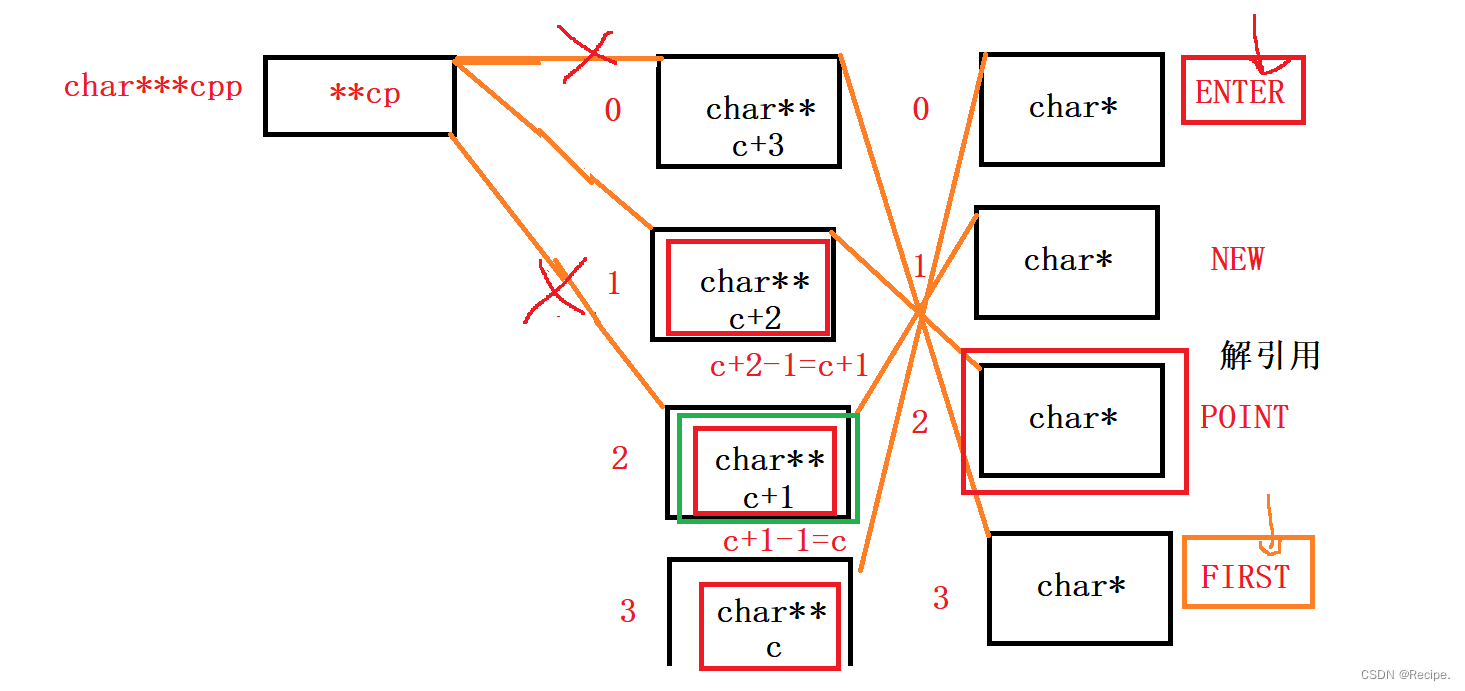
C语言——指针题目“指针探测器“
如果你觉得你指针学的自我感觉良好,甚至已经到达了炉火纯青的地步,不妨来试试这道题目? #include<stdio.h> int main() {char* c[] { "ENTER","NEW","POINT","FIRST" };char** cp[] { c 3…...
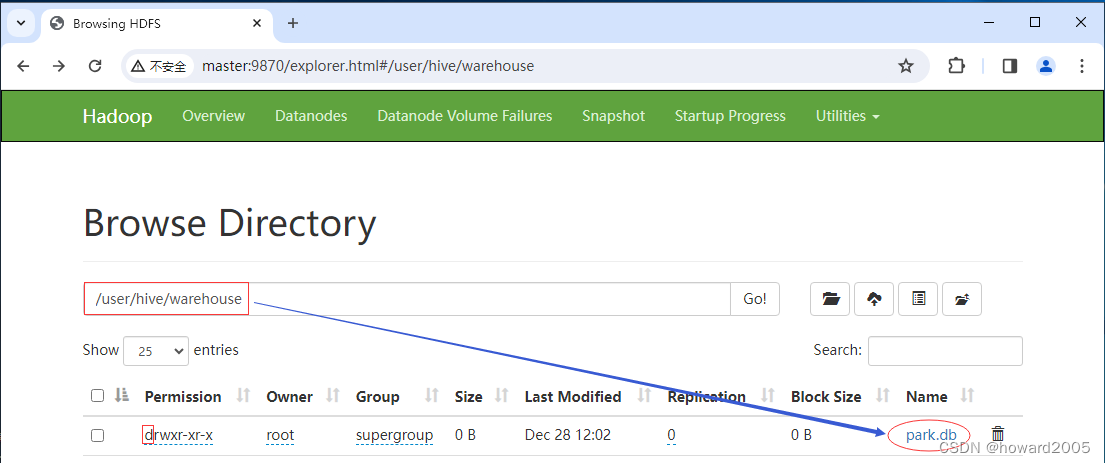
Hive讲课笔记:内部表与外部表
文章目录 一、导言二、内部表1.1 什么是内部表1.1.1 内部表的定义1.1.2 内部表的关键特性 1.2 创建与操作内部表1.2.1 创建并查看数据库1.2.2 在park数据库里创建student表1.2.3 在student表插入一条记录1.2.4 通过HDFS WebUI查看数据库与表 三、外部表2.1 什么是外部表2.2 创建…...

Docker本地部署开源浏览器Firefox并远程访问进行测试
文章目录 1. 部署Firefox2. 本地访问Firefox3. Linux安装Cpolar4. 配置Firefox公网地址5. 远程访问Firefox6. 固定Firefox公网地址7. 固定地址访问Firefox Firefox是一款免费开源的网页浏览器,由Mozilla基金会开发和维护。它是第一个成功挑战微软Internet Explorer浏…...

PHP:服务器端脚本语言的瑰宝
PHP(Hypertext Preprocessor)是一种广泛应用于服务器端编程的开源脚本语言,它以其简单易学、灵活性和强大的功能而成为Web开发的瑰宝。本文将深入介绍PHP的历史、特性、用途以及与生态系统的关系,为读者提供对这门语言全面的了解。…...

【MySQL】数据库并发控制:悲观锁与乐观锁的深入解析
🍎个人博客:个人主页 🏆个人专栏: 数 据 库 ⛳️ 功不唐捐,玉汝于成 目录 前言 正文 悲观锁(Pessimistic Locking): 乐观锁(Optimistic Locking): 总结&#x…...

作业--day38
1.定义一个Person类,包含私有成员,int *age,string &name,一个Stu类,包含私有成员double *score,Person p1,写出Person类和Stu类的特殊成员函数,并写一个Stu的show函数ÿ…...

pytest 的 fixture 固件机制
一、前置说明 固件(fixture)是一些函数,pytest 会在执行测试函数之前(或之后)加载运行它们。pytest 使用 fixture 固件机制来实现测试的前置和后置操作,可以方便地设置和共享测试环境。 二、操作步骤 1. 编写测试代码 atme/demos/demo_pytest_tutorials/test_pytest_…...

分布式技术之分布式计算Stream模式
文章目录 什么是 Stream?Stream 工作原理Storm 的工作原理 实时性任务主要是针对流数据的处理,对处理时延要求很高,通常需要有常驻服务进程,等待数据的随时到来随时处理,以保证低时延。处理流数据任务的计算模式&#…...

2023年12月GESP Python五级编程题真题解析
【五级编程题1】 【试题名称】:小杨的幸运数 【问题描述】 小杨认为,所有大于等于a的完全平方数都是他的超级幸运数。 小杨还认为,所有超级幸运数的倍数都是他的幸运数。自然地,小杨的所有超级幸运数也都是幸运数。 对于一个…...
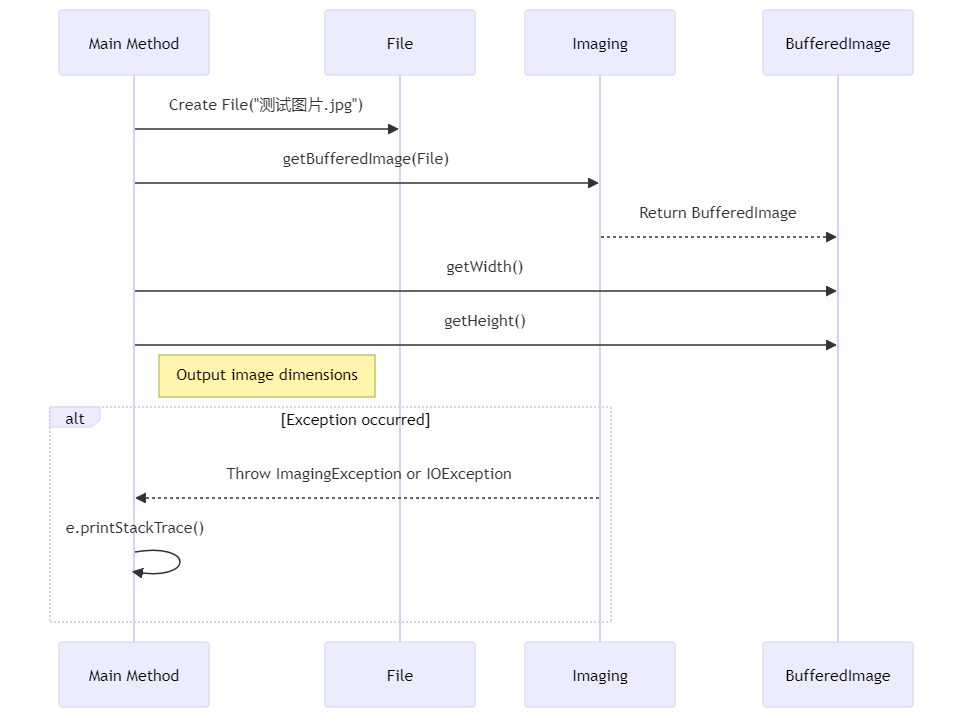
探索Apache Commons Imaging处理图像
第1章:引言 大家好,我是小黑,咱们今天来聊聊图像处理。在这个数字化日益增长的时代,图像处理已经成为了一个不可或缺的技能。不论是社交媒体上的照片编辑,还是专业领域的图像分析,图像处理无处不在。而作为…...

ES6从入门到精通:前言
ES6简介 ES6(ECMAScript 2015)是JavaScript语言的重大更新,引入了许多新特性,包括语法糖、新数据类型、模块化支持等,显著提升了开发效率和代码可维护性。 核心知识点概览 变量声明 let 和 const 取代 var…...
)
【位运算】消失的两个数字(hard)
消失的两个数字(hard) 题⽬描述:解法(位运算):Java 算法代码:更简便代码 题⽬链接:⾯试题 17.19. 消失的两个数字 题⽬描述: 给定⼀个数组,包含从 1 到 N 所有…...

Vue2 第一节_Vue2上手_插值表达式{{}}_访问数据和修改数据_Vue开发者工具
文章目录 1.Vue2上手-如何创建一个Vue实例,进行初始化渲染2. 插值表达式{{}}3. 访问数据和修改数据4. vue响应式5. Vue开发者工具--方便调试 1.Vue2上手-如何创建一个Vue实例,进行初始化渲染 准备容器引包创建Vue实例 new Vue()指定配置项 ->渲染数据 准备一个容器,例如: …...

使用 SymPy 进行向量和矩阵的高级操作
在科学计算和工程领域,向量和矩阵操作是解决问题的核心技能之一。Python 的 SymPy 库提供了强大的符号计算功能,能够高效地处理向量和矩阵的各种操作。本文将深入探讨如何使用 SymPy 进行向量和矩阵的创建、合并以及维度拓展等操作,并通过具体…...

【电力电子】基于STM32F103C8T6单片机双极性SPWM逆变(硬件篇)
本项目是基于 STM32F103C8T6 微控制器的 SPWM(正弦脉宽调制)电源模块,能够生成可调频率和幅值的正弦波交流电源输出。该项目适用于逆变器、UPS电源、变频器等应用场景。 供电电源 输入电压采集 上图为本设计的电源电路,图中 D1 为二极管, 其目的是防止正负极电源反接, …...

【SSH疑难排查】轻松解决新版OpenSSH连接旧服务器的“no matching...“系列算法协商失败问题
【SSH疑难排查】轻松解决新版OpenSSH连接旧服务器的"no matching..."系列算法协商失败问题 摘要: 近期,在使用较新版本的OpenSSH客户端连接老旧SSH服务器时,会遇到 "no matching key exchange method found", "n…...
提供了哪些便利?)
现有的 Redis 分布式锁库(如 Redisson)提供了哪些便利?
现有的 Redis 分布式锁库(如 Redisson)相比于开发者自己基于 Redis 命令(如 SETNX, EXPIRE, DEL)手动实现分布式锁,提供了巨大的便利性和健壮性。主要体现在以下几个方面: 原子性保证 (Atomicity)ÿ…...
)
GitHub 趋势日报 (2025年06月06日)
📊 由 TrendForge 系统生成 | 🌐 https://trendforge.devlive.org/ 🌐 本日报中的项目描述已自动翻译为中文 📈 今日获星趋势图 今日获星趋势图 590 cognee 551 onlook 399 project-based-learning 348 build-your-own-x 320 ne…...

高考志愿填报管理系统---开发介绍
高考志愿填报管理系统是一款专为教育机构、学校和教师设计的学生信息管理和志愿填报辅助平台。系统基于Django框架开发,采用现代化的Web技术,为教育工作者提供高效、安全、便捷的学生管理解决方案。 ## 📋 系统概述 ### 🎯 系统定…...

解析两阶段提交与三阶段提交的核心差异及MySQL实现方案
引言 在分布式系统的事务处理中,如何保障跨节点数据操作的一致性始终是核心挑战。经典的两阶段提交协议(2PC)通过准备阶段与提交阶段的协调机制,以同步决策模式确保事务原子性。其改进版本三阶段提交协议(3PC…...
