MIT线性代数笔记-第27讲-复数矩阵,快速傅里叶变换
目录
- 27.复数矩阵,快速傅里叶变换
- 打赏
27.复数矩阵,快速傅里叶变换
对于实矩阵而言,特征值为复数时,特征向量一定为复向量,由此引入对复向量的学习
-
求模长及内积
假定一个复向量 z ⃗ = [ z 1 z 2 ⋮ z n ] \vec{z} = \begin{bmatrix} z_1 \\ z_2 \\ \vdots\\ z_n \end{bmatrix} z= z1z2⋮zn ,其中 z 1 , z 2 , ⋯ , z n z_1 , z_2 , \cdots , z_n z1,z2,⋯,zn为复数,所以该向量不再属于 R n R^n Rn,而是属于 n n n维复空间 C n C^n Cn
显然再使用 z ⃗ T z ⃗ \sqrt{\vec{z}^T \vec{z}} zTz无法求出模长,比如对于 z ⃗ = [ 1 i ] \vec{z} = \begin{bmatrix} 1 \\ i \end{bmatrix} z=[1i]有 z ⃗ T z ⃗ = [ 1 i ] [ 1 i ] = 0 ≠ 2 \sqrt{\vec{z}^T \vec{z}} = \begin{bmatrix} 1 & i \end{bmatrix} \begin{bmatrix} 1 \\ i \end{bmatrix} = 0 \ne \sqrt{2} zTz=[1i][1i]=0=2
由上一讲的内容可以得到 ∣ z ⃗ ∣ = z ⃗ ‾ T z ⃗ |\vec{z}| = \sqrt{\overline{\vec{z}}^T \vec{z}} ∣z∣=zTz,我们把求共轭和转置两步操作一起记作 H H H(来自 H e r m i t e Hermite Hermite),即 z ⃗ H = z ⃗ ‾ T \vec{z}^H = \overline{\vec{z}}^T zH=zT
同理,求内积时也使用 H H H,即对于两个复向量 x ⃗ , y ⃗ \vec{x} , \vec{y} x,y,有 x ⃗ ⋅ y ⃗ = x ⃗ H y ⃗ \vec{x} \cdot \vec{y} = \vec{x}^H \vec{y} x⋅y=xHy,此时内积为 0 0 0仍然可以说明向量正交,对于矩阵也类似
-
对称矩阵的推广
对于实矩阵,对称矩阵即满足 A T = A A^T = A AT=A的矩阵,推广到复矩阵,我们把满足 A H = A A^H = A AH=A的矩阵称作厄米特矩阵
可以发现厄米特矩阵的对角线元素均为实数,因为它们在转置时不变,所以在求共轭时也不变,其它元素与转置后的对应元素互为共轭
由上一讲可知厄米特矩阵的特征值一定为实数
-
正交矩阵的推广
对于实矩阵,正交矩阵即满足 Q T Q = I Q^T Q = I QTQ=I的方阵,推广到复矩阵,我们把满足 Q H Q = I Q^H Q= I QHQ=I的方阵称作酉矩阵
可以发现酉矩阵的列向量组成复空间下的一组标准正交基,其转置与正交一致且均为酉矩阵
-
傅里叶矩阵
傅里叶变换是一种分析信号的方法,它可分析信号的成分,也可用这些成分合成信号。许多波形可作为信号的成分,比如正弦波、方波、锯齿波等,傅里叶变换用正弦波作为信号的成分。由于傅里叶变换经常用在计算机上,而在电子工程或计算机中,方阵的行和列都是从 0 0 0开始到 n − 1 n - 1 n−1结束的,所以在讨论傅里叶矩阵时遵从这种下标规则。
傅里叶矩阵是一种酉矩阵,它满足 ( F n ) i , j = 1 n w i ∗ j , i , j = 0 , ⋯ , n − 1 (F_n)_{i , j} = \dfrac{1}{n} w^{i * j} , i , j = 0 , \cdots , n - 1 (Fn)i,j=n1wi∗j,i,j=0,⋯,n−1( w = e 2 π i / n w = e^{2 \pi i / n} w=e2πi/n),即:
F n = 1 n [ 1 1 1 ⋯ 1 1 w w 2 ⋯ w n − 1 1 w 2 w 4 ⋯ w 2 ( n − 1 ) ⋮ ⋮ ⋮ ⋱ ⋮ 1 w n − 1 w 2 ( n − 1 ) ⋯ w ( n − 1 ) 2 ] F_n = \dfrac{1}{n} \begin{bmatrix} 1 & 1 & 1 & \cdots & 1 \\ 1 & w & w^2 & \cdots & w^{n - 1} \\ 1 & w^2 & w^4 & \cdots & w^{2(n - 1)} \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ 1 & w^{n - 1} & w^{2(n - 1)} & \cdots & w^{(n - 1)^2} \end{bmatrix} Fn=n1 111⋮11ww2⋮wn−11w2w4⋮w2(n−1)⋯⋯⋯⋱⋯1wn−1w2(n−1)⋮w(n−1)2
可以发现 w = e 2 π i / n = c o s 2 π n + i s i n 2 π n w = e^{2 \pi i / n} = cos\ \dfrac{2 \pi}{n} + i sin\ \dfrac{2 \pi}{n} w=e2πi/n=cos n2π+isin n2π,落在复平面原点为圆心的单位圆上,且对应的角度为一圈的 1 n \dfrac{1}{n} n1,所以 w w w乘上自己相当于增加角度 2 π n \dfrac{2 \pi}{n} n2π,因此 w k n = ( w n ) k = 1 , k ∈ Z w^{kn} = (w^n)^k = 1 , k \in Z wkn=(wn)k=1,k∈Z
证明傅里叶矩阵是酉矩阵:
设 F n F_n Fn的列向量分别为 f ⃗ 0 , f ⃗ 2 , ⋯ , f ⃗ n − 1 \vec{f}_0 , \vec{f}_2 , \cdots , \vec{f}_{n - 1} f0,f2,⋯,fn−1,即证 f ⃗ a H f ⃗ b = { 0 , a ≠ b 1 , a = b \vec{f}_a^H \vec{f}_b = \left\{\begin{matrix} 0 , a \ne b \\ 1,a = b \end{matrix}\right. faHfb={0,a=b1,a=b
f ⃗ a H f ⃗ b = ( F n ) 0 , a ‾ ∗ ( F n ) 0 , b + ( F n ) 1 , a ‾ ∗ ( F n ) 1 , b + ⋯ + ( F n ) n − 1 , a ‾ ∗ ( F n ) n − 1 , b = w 0 ( a + b ) + w a + b + ⋯ + w ( n − 1 ) ( a + b ) \begin{aligned} \vec{f}_a^H \vec{f}_b & = \overline{(F_n)_{0 , a}} * (F_n)_{0 , b} + \overline{(F_n)_{1 , a}} * (F_n)_{1 , b} + \cdots + \overline{(F_n)_{n - 1 , a}} * (F_n)_{n - 1 , b} \\ & = w^{0(a + b)} + w^{a + b} + \cdots + w^{(n - 1)(a + b)} \end{aligned} faHfb=(Fn)0,a∗(Fn)0,b+(Fn)1,a∗(Fn)1,b+⋯+(Fn)n−1,a∗(Fn)n−1,b=w0(a+b)+wa+b+⋯+w(n−1)(a+b)
暂时不会证明 \color{OrangeRed}暂时不会证明 暂时不会证明
-
傅里叶变换
当 n = 4 n = 4 n=4时, 2 π n = π 2 \dfrac{2 \pi}{n} = \dfrac{\pi}{2} n2π=2π,所以 w w w的乘方落在实轴和虚轴上2,由此得到四阶傅里叶矩阵 F 4 = 1 4 [ 1 1 1 1 1 i − 1 − i 1 − 1 1 − 1 1 − i − 1 i ] F_4 = \dfrac{1}{4} \begin{bmatrix} 1 & 1 & 1 & 1 \\ 1 & i & -1 & -i \\ 1 & -1 & 1 & -1 \\ 1 & -i & -1 & i \end{bmatrix} F4=41 11111i−1−i1−11−11−i−1i
用 F 4 F_4 F4左乘四维向量即为四点离散傅里叶变换( D F T DFT DFT),用 F 4 − 1 F_4^{-1} F4−1左乘四维向量即为傅里叶逆变换
-
快速傅里叶变换
实际上可以将傅里叶矩阵分解为一系列“稀疏矩阵”,这些矩阵具有大量零元素,可以很方便地求逆及用于相乘
现在考虑 F 64 F_{64} F64与 F 32 F_{32} F32之间的联系,假设 F 32 , F 64 F_{32} , F_{64} F32,F64中的 w w w分别为 w 32 , w 64 w_{32} , w_{64} w32,w64,则 w 64 2 = w 32 w_{64}^2 = w_{32} w642=w32
先说结论: F 64 = 1 2 [ I D I − D ] [ F 32 O O F 32 ] [ 1 0 0 0 ⋯ 0 0 1 0 ⋯ ⋮ ⋮ ⋮ ⋮ ⋮ 0 1 0 0 ⋯ 0 0 0 1 ⋯ ⋮ ⋮ ⋮ ⋮ ⋮ ] F_{64} = \dfrac{1}{2} \begin{bmatrix} I & D \\ I & -D\end{bmatrix} \begin{bmatrix} F_{32} & O \\ O & F_{32}\end{bmatrix} \begin{bmatrix} 1 & 0 & 0 & 0 & \cdots \\ 0 & 0 & 1 & 0 & \cdots \\ \vdots & \vdots & \vdots & \vdots & \vdots \\ 0 & 1 & 0 & 0 & \cdots \\ 0 & 0 & 0 & 1 & \cdots \\ \vdots & \vdots & \vdots & \vdots & \vdots \end{bmatrix} F64=21[IID−D][F32OOF32] 10⋮00⋮00⋮10⋮01⋮00⋮00⋮01⋮⋯⋯⋮⋯⋯⋮ ,其中 D = [ 1 0 0 ⋯ 0 0 w 0 ⋯ 0 0 0 w 64 2 ⋯ 0 ⋮ ⋮ ⋮ ⋱ ⋮ 0 0 0 ⋯ w 64 31 ] D = \begin{bmatrix} 1 & 0 & 0 & \cdots & 0 \\ 0 & w_{} & 0 & \cdots & 0 \\ 0 & 0 & w_{64}^2 & \cdots & 0 \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & 0 & \cdots & w_{64}^{31} \end{bmatrix} D= 100⋮00w0⋮000w642⋮0⋯⋯⋯⋱⋯000⋮w6431
证明: 可以发现 F 64 F_{64} F64拆分出的第三个矩阵将用于进行傅里叶变换的向量的偶数位元素提到了前面而将奇数位元素放到了后面,然后拆分出的第二个矩阵对刚才得到的新向量中的前后两部分分别做一次 32 32 32阶傅里叶变换
对于新向量前半部分,第 i i i个元素在求 32 32 32阶傅里叶变换后的第 j j j行时乘上了 w 32 j i w_{32}^{ji} w32ji,而新向量前半部分的第 i i i个元素是原向量的第 2 ∗ i 2*i 2∗i个元素,这说明它在求 64 64 64阶傅里叶变换后的第 j j j行时应该乘上 w 64 2 j i w_{64}^{2ji} w642ji,刚好 w 32 j i = w 64 2 j i w_{32}^{ji} = w_{64}^{2ji} w32ji=w642ji,所以 F 64 F_{64} F64拆分出的第一个矩阵左半部分上方是单位向量,对于下方,新向量前半部分的第 i i i个元素在求 64 64 64阶傅里叶变换后的第 32 + j 32 + j 32+j行时应乘上 w 64 2 ( 32 + j ) i = w 32 ( 32 + j ) i = w 32 j i w 32 32 i = w 32 j i ( − 1 ) i = w 32 j i w_{64}^{2(32 + j)i} = w_{32}^{(32 + j)i} = w_{32}^{ji} w_{32}^{32i} = w_{32}^{ji} (-1)^i = w_{32}^{ji} w642(32+j)i=w32(32+j)i=w32jiw3232i=w32ji(−1)i=w32ji,所以左半部分下方也是单位矩阵
对于新向量后半部分,第 i i i个元素在求 32 32 32阶傅里叶变换后的第 j j j行时乘上了 w 32 j i w_{32}^{ji} w32ji,而在求 64 64 64阶傅里叶变换后的第 j j j行时应该乘上 w 64 j ( 2 i + 1 ) w_{64}^{j(2i + 1)} w64j(2i+1),即 w 32 j i ∗ w 64 j w_{32}^{ji} * w_{64}^j w32ji∗w64j,由此得到 D D D,对于拆分出的第一个矩阵右半部分下方,新向量后半部分的第 i i i个元素在求 64 64 64阶傅里叶变换后的第 32 + j 32 + j 32+j行时应乘上 w 64 2 ( 32 + j ) i = w 32 j i ( − 1 ) i = − w 32 j i w_{64}^{2(32 + j)i} = w_{32}^{ji} (-1)^i = -w_{32}^{ji} w642(32+j)i=w32ji(−1)i=−w32ji,所以右半部分下方是 − D -D −D
最后说明 1 2 \dfrac{1}{2} 21,因为前面进行 32 32 32阶傅里叶变换时只除以了 32 32 32,所以最后还要再除以 2 2 2才能达到除以 64 64 64
为了直观地说明,此处只证明了 F 64 F_{64} F64到 F 32 F_{32} F32的拆分,对于 F 2 n F_{2n} F2n到 F n F_n Fn的拆分,将具体的数字换为字母后也可得证
直接进行 64 64 64阶傅里叶变换的时间复杂度是 O ( n 2 ) O(n^2) O(n2),而拆分为三个矩阵后,第三个矩阵和原向量相乘时间复杂度为 O ( n ) O(n) O(n),第二个矩阵和新向量相乘时间复杂度为 O ( n 2 2 ) O(\dfrac{n^2}{2}) O(2n2),此时得到的向量和第一个矩阵相乘时间复杂度为 O ( n ) O(n) O(n),总时间复杂度为 O ( 2 ( n 2 ) 2 + n ) O(2 (\dfrac{n}{2})^2 + n) O(2(2n)2+n),当然这还没有结束,因为第二个矩阵的 F 32 F_{32} F32可以进行类似的拆分得到含有 F 16 F_{16} F16的三个矩阵,这样刚才求得的总时间复杂度进一步简化得到 O ( 2 ( 2 ( n 4 ) 2 + n 2 ) + n ) = O ( 2 2 ( n 4 ) 2 + 2 n ) O(2(2 (\dfrac{n}{4})^2 + \dfrac{n}{2}) + n) = O(2^2 (\dfrac{n}{4})^2 + 2n) O(2(2(4n)2+2n)+n)=O(22(4n)2+2n),以此类推,一层层拆分下去,时间复杂度就会降为 O ( n + n l o g n ) O(n + n\ log\ n) O(n+n log n),即 O ( n l o g n ) O(n\ log\ n) O(n log n)
打赏
制作不易,若有帮助,欢迎打赏!


相关文章:

MIT线性代数笔记-第27讲-复数矩阵,快速傅里叶变换
目录 27.复数矩阵,快速傅里叶变换打赏 27.复数矩阵,快速傅里叶变换 对于实矩阵而言,特征值为复数时,特征向量一定为复向量,由此引入对复向量的学习 求模长及内积 假定一个复向量 z ⃗ [ z 1 z 2 ⋮ z n ] \vec{z} \…...

三维点通用排序
前言 NWAFU 2021阶段二 C 一、题目描述 题目描述 在三维笛卡尔坐标系中,可以用X,Y,Z三个坐标分量表示三维空间中的一个点。现有一系列用X,Y,Z表示的三维点,需要对其按指定的X、Y或Z分量进行升序或降序排序。请用C语言实现这一排序过程,程序…...

[架构之路-265]:目标系统 - 设计方法 - 软件工程 - 软件设计 - 如何做好详细设计
目录 一、详细设计概述 1.1 什么是详细设计 1.2 软件概要设计、软件架构、软件详细设计比较 二、软件详细设计说明书 2.1 概述 2.2 撰写步骤 2.3 主要内容 三、详细设计详解 3.1 引言 3.2 系统架构设计 3.3 模块设计 3.3.1 模块描述 3.3.2 模块间接口设计与UML图 …...
java设计模式学习之【模板方法模式】
文章目录 引言模板方法模式简介定义与用途实现方式 使用场景优势与劣势在Spring框架中的应用游戏设计示例代码地址 引言 设想你正在准备一顿晚餐,无论你想做意大利面、披萨还是沙拉,制作过程中都有一些共同的步骤:准备原料、加工食物、摆盘。…...

篇章二 | Python 入门指南:深入理解基础数据类型
Python 是一门强大而易学的编程语言,而深刻理解其基础数据类型是掌握 Python 编程的重要一步。本入门指南将详细介绍 Python 中的基础数据类型,包括整数、浮点数、字符串、布尔值、列表、元组、字典和集合等,同时提供注意事项和与 C 语言的区…...

循环冗余效验码的计算方法
循环冗余效验码的计算方法 G(x): 在了解计算方法之前我们首先要明白G(x)表明的意思,这一步非常重要! 例如,G(x) x^3 x^2 1 ,该式子表明的编…...
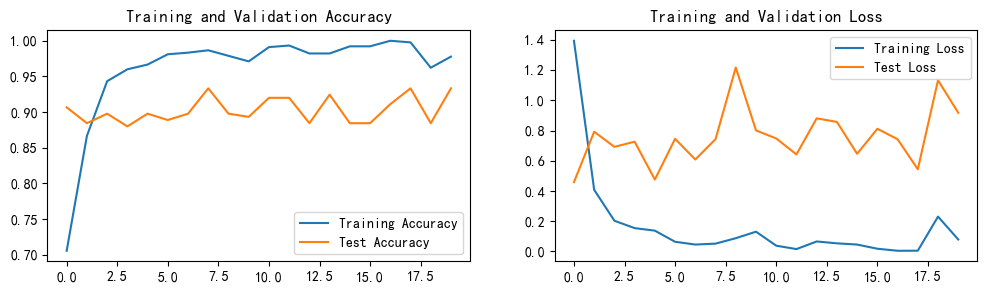
第P8周:YOLOv5-C3模块实现
>- **🍨 本文为[🔗365天深度学习训练营](https://mp.weixin.qq.com/s/rbOOmire8OocQ90QM78DRA) 中的学习记录博客** >- **🍖 原作者:[K同学啊 | 接辅导、项目定制](https://mtyjkh.blog.csdn.net/)** 一、 前期准备 1. 设…...
)
Java中常见的日志包分析(Log4j、Logback、SLF4J等)
Java中常见的日志jar包包括Log4j、Logback、SLF4J、java.util.logging等。它们各自的作用和应用场景如下: 1. Log4j 作用:Log4j是Apache的一个开源项目,提供日志记录的功能,支持多种输出目的地,如控制台、文件、GUI组…...

C++系列-第1章顺序结构-3-输出类cout
C系列-第1章顺序结构-3-输出类cout 在线练习: http://noi.openjudge.cn/ https://www.luogu.com.cn/ 总结 本文是C系列博客,主要讲述输出类cout的用法 cout介绍与基本用法 在C中,cout 是用于输出(打印)数据的工具&…...

对于智能设备的一些设想1
最近发现脑子里经常会出现一些能够偷懒的想法,希望这些点子能一点点保存下来,希望有需要的人拿走点子,不用谢 1.泡脚桶 2023年12月28日 近两年泡脚桶的风着实很大,我差点也就入坑了,于是有了一种设想,为什么…...

Large-Precision Sign using PBS
参考文献: [CLOT21] Chillotti I, Ligier D, Orfila J B, et al. Improved programmable bootstrapping with larger precision and efficient arithmetic circuits for TFHE[C]//Advances in Cryptology–ASIACRYPT 2021: 27th International Conference on the T…...

【电商项目实战】MD5登录加密及JSR303自定义注解
🎉🎉欢迎来到我的CSDN主页!🎉🎉 🏅我是Java方文山,一个在CSDN分享笔记的博主。📚📚 🌟推荐给大家我的专栏《电商项目实战》。🎯🎯 &am…...

2014,TEVC,A competitive swarm optimizer for large scale optimization(CSO)
PSO 分析(从而引入 CSO) CSO (competitive swarm optimizer) 算法是在PSO (particle swarm optimization) 算法的基础上改进而来的。PSO算法是一种功能强大、应用广泛的群体智能算法,主要用来解决优化问题。PSO算法包含一个粒子群࿰…...

【机器学习】【线性回归】梯度下降
文章目录 [toc]数据集实际值估计值估计误差代价函数学习率参数更新Python实现导包数据预处理迭代过程数据可视化完整代码 线性拟合结果代价结果 个人主页:丷从心 系列专栏:机器学习 数据集 ( x ( i ) , y ( i ) ) , i 1 , 2 , ⋯ , m \left(x^{(i)} , …...
JMeter逻辑控制器之While控制器
JMeter逻辑控制器之While控制器 1. 背景2.目的3. 介绍4.While示例4.1 添加While控制器4.2 While控制器面板4.3 While控制器添加请求4.3 While控制器应用场景 1. 背景 存在一些使用场景,比如:某个请求必须等待上一个请求正确响应后才能开始执行。或者&…...

记录 Docker 外部访问的基本操作
目录 1. 启动 docker 时挂载本地目录2. 外部访问 docker 容器 (-p/-P)3. 无法连接 docker 内 SSH 解决方案 1. 启动 docker 时挂载本地目录 # 将本地 D:/SDK 目录 挂载到 容器里的 /mnt/host 目录中 # 注意:-v /d/SDK:/mnt/host/ 必须放到 IMAGE_ID 前面才行 # …...
:BannerMessagePreference)
【Android 13】使用Android Studio调试系统应用之Settings移植(六):BannerMessagePreference
文章目录 一、篇头二、系列文章2.1 Android 13 系列文章2.2 Android 9 系列文章2.3 Android 11 系列文章三、BannerMessagePreference的移植3.1 新的问题:找不到 R.dimen.settingslib_preferred_minimum_touch_target3.2 问题分析(一)3.2.1 资源定义的位置3.2.2 检查依赖3.2…...

Python 变量
打印输出内容 print(‘rumenle’) print(‘haode’) 缩进需要tab 注释将需要注释的部分开头用# 多行注释 1、用你也可以左键选中我们需要注释的代码,松开,按:Ctrl/,就完成相同效果注释 2、把要注释的内容放到三个引号对里面 …...

ComfyUI如何中文汉化
comfyui中文地址如下: https://github.com/AIGODLIKE/AIGODLIKE-ComfyUI-Translationhttps://github.com/AIGODLIKE/AIGODLIKE-ComfyUI-Translation如何安装? 1. git安装 进入项目目录下的custom_nodes目录下,然后进入控制台,运…...
Glary Utilities Pro - 电脑系统优化全面指南:详尽使用教程
软件简介: Glary Utilities Pro 是一款全面的电脑优化工具,它旨在帮助用户提升计算机的性能和稳定性。这款软件提供了多种功能,包括系统清理、优化、修复以及保护。通过一键扫描,它可以识别并清除无用文件、临时数据、注册表错误等…...

【WiFi帧结构】
文章目录 帧结构MAC头部管理帧 帧结构 Wi-Fi的帧分为三部分组成:MAC头部frame bodyFCS,其中MAC是固定格式的,frame body是可变长度。 MAC头部有frame control,duration,address1,address2,addre…...

从零实现富文本编辑器#5-编辑器选区模型的状态结构表达
先前我们总结了浏览器选区模型的交互策略,并且实现了基本的选区操作,还调研了自绘选区的实现。那么相对的,我们还需要设计编辑器的选区表达,也可以称为模型选区。编辑器中应用变更时的操作范围,就是以模型选区为基准来…...

Redis相关知识总结(缓存雪崩,缓存穿透,缓存击穿,Redis实现分布式锁,如何保持数据库和缓存一致)
文章目录 1.什么是Redis?2.为什么要使用redis作为mysql的缓存?3.什么是缓存雪崩、缓存穿透、缓存击穿?3.1缓存雪崩3.1.1 大量缓存同时过期3.1.2 Redis宕机 3.2 缓存击穿3.3 缓存穿透3.4 总结 4. 数据库和缓存如何保持一致性5. Redis实现分布式…...

2021-03-15 iview一些问题
1.iview 在使用tree组件时,发现没有set类的方法,只有get,那么要改变tree值,只能遍历treeData,递归修改treeData的checked,发现无法更改,原因在于check模式下,子元素的勾选状态跟父节…...

ArcGIS Pro制作水平横向图例+多级标注
今天介绍下载ArcGIS Pro中如何设置水平横向图例。 之前我们介绍了ArcGIS的横向图例制作:ArcGIS横向、多列图例、顺序重排、符号居中、批量更改图例符号等等(ArcGIS出图图例8大技巧),那这次我们看看ArcGIS Pro如何更加快捷的操作。…...

高效线程安全的单例模式:Python 中的懒加载与自定义初始化参数
高效线程安全的单例模式:Python 中的懒加载与自定义初始化参数 在软件开发中,单例模式(Singleton Pattern)是一种常见的设计模式,确保一个类仅有一个实例,并提供一个全局访问点。在多线程环境下,实现单例模式时需要注意线程安全问题,以防止多个线程同时创建实例,导致…...

佰力博科技与您探讨热释电测量的几种方法
热释电的测量主要涉及热释电系数的测定,这是表征热释电材料性能的重要参数。热释电系数的测量方法主要包括静态法、动态法和积分电荷法。其中,积分电荷法最为常用,其原理是通过测量在电容器上积累的热释电电荷,从而确定热释电系数…...

并发编程 - go版
1.并发编程基础概念 进程和线程 A. 进程是程序在操作系统中的一次执行过程,系统进行资源分配和调度的一个独立单位。B. 线程是进程的一个执行实体,是CPU调度和分派的基本单位,它是比进程更小的能独立运行的基本单位。C.一个进程可以创建和撤销多个线程;同一个进程中…...
的打车小程序)
基于鸿蒙(HarmonyOS5)的打车小程序
1. 开发环境准备 安装DevEco Studio (鸿蒙官方IDE)配置HarmonyOS SDK申请开发者账号和必要的API密钥 2. 项目结构设计 ├── entry │ ├── src │ │ ├── main │ │ │ ├── ets │ │ │ │ ├── pages │ │ │ │ │ ├── H…...

加密通信 + 行为分析:运营商行业安全防御体系重构
在数字经济蓬勃发展的时代,运营商作为信息通信网络的核心枢纽,承载着海量用户数据与关键业务传输,其安全防御体系的可靠性直接关乎国家安全、社会稳定与企业发展。随着网络攻击手段的不断升级,传统安全防护体系逐渐暴露出局限性&a…...
