【C语言】数据结构——排序二(快排)
💗个人主页💗
⭐个人专栏——数据结构学习⭐
💫点击关注🤩一起学习C语言💯💫
目录
- 导读:
- 数组打印与交换
- 1. 交换排序
- 1.1 基本思想:
- 1.2 冒泡与快排的异同
- 2. 冒泡排序
- 2.1 基本思想
- 2.2 实现代码
- 3. 快速排序
- 3.1 基本思想
- 3.2 hoare版本
- 3.2.1 动图讲解
- 3.2.2 实现代码
- 3.2.3 代码优化
- 3.3 挖坑法
- 3.3.1 动图详解
- 3.3.2实现代码
- 3.4 双指针
- 3.4.1 动图详解
- 3.4.2 实现代码
- 4. 无递归实现快排
- 4.1 基本思想
- 4.2 实现代码
导读:
我们在前面学习了排序,包括直接插入排序,希尔排序,选择排序,堆排序。
今天我们来学习交换排序,也就是冒泡排序和快排。
下期我们来讲一讲归并排序。
关注博主或是订阅专栏,掌握第一消息。
数组打印与交换
为了方便我们来测试每个排序是否完成,我们来写个打印数组和交换两数的函数,方便我们后续的打印与交换。
void PrintArray(int* a, int n)
{for (int i = 0; i < n; i++){printf("%d ", a[i]);}printf("\n");
}void Swap(int* p1, int* p2)
{int tmp = *p1;*p1 = *p2;*p2 = tmp;
}
1. 交换排序
1.1 基本思想:
所谓交换,就是根据序列中两个记录键值的比较结果来对换这两个记录在序列中的位置。将键值较大的记录向序列的尾部移动,键值较小的记录向序列的前部移动。
交换排序包括冒泡排序与快速排序。
1.2 冒泡与快排的异同
相似之处:
都是基于比较的排序算法,通过比较元素的大小来确定它们的顺序。
不同之处:
思想不同:冒泡排序是通过相邻元素的比较和交换来将较大的元素“浮”到序列的末尾,而快速排序是通过在序列中选择一个基准元素,将序列分割成两个子序列,并递归地对子序列进行排序。
时间复杂度不同:冒泡排序的平均时间复杂度为O(n2),最好情况下为O(n),最坏情况下为O(n2)。快速排序的平均时间复杂度为O(nlogn),最坏情况下为O(n^2)。
空间复杂度不同:冒泡排序的空间复杂度为O(1),原地排序。快速排序的空间复杂度为O(logn),需要使用递归栈空间。
稳定性不同:冒泡排序是稳定的排序算法,相等元素的相对顺序不会改变。快速排序是不稳定的排序算法,相等元素的相对顺序可能会改变。
总结:冒泡排序和快速排序都是基于比较的排序算法,它们的主要区别在于思想、时间复杂度、空间复杂度和稳定性等方面。快速排序通常比冒泡排序更高效,但在某些情况下冒泡排序可能更适合,例如对较小规模的数据进行排序。
2. 冒泡排序
2.1 基本思想
冒泡排序算法的基本思想是要将待排序序列中的元素逐个比较并交换位置,使得较大的元素逐渐“浮”到序列的末尾。
从待排序序列的第一个元素开始,逐个比较相邻的两个元素。
如果前一个元素比后一个元素大,则交换它们的位置。这样就使得较大的元素逐渐“浮”到序列的末尾。
继续对剩下的元素重复上述比较和交换的过程,直到整个序列有序为止。
重复上述步骤,每次将待排序序列的长度减1,直到待排序序列的长度为1。
冒泡排序算法的思想类似于水中冒泡,较大的元素会逐渐向上浮动,而较小的元素会逐渐沉淀到底部。因此,最终结果是将待排序序列从小到大排序。
冒泡排序算法的时间复杂度为O(n^2),其中n为待排序序列的长度。尽管冒泡排序算法的效率相对较低,但由于其实现简单,适用于数据量较小的情况。
2.2 实现代码
// 冒泡排序
void BubbleSort(int* a, int n)
{int i = 0;int j = 0;for (i = 0; i < n; i++){for (j = 0; j < n - i -1; j++){if (a[j + 1] < a[j]){Swap(&a[j + 1], &a[j]);}}}
}
void TestBubbleSort()
{int arr[10] = { 5, 1, 8, 7, 3, 9, 2, 0, 4, 6 };int sz = sizeof(arr) / sizeof(arr[0]);BubbleSort(arr, 10);PrintArray(arr, 10);
}
int main()
{TestBubbleSort();return 0;
}
3. 快速排序
快速排序有三种实现方法:
- hoare版本
- 挖坑法
- 双指针
3.1 基本思想
快速排序是一种基于分治思想的排序算法,其基本思想可以概括为以下步骤:
选择一个基准元素:从待排序序列中选择一个元素作为基准元素。
分割操作:以基准元素为准,将序列分割成两个子序列,使得左边的子序列中的所有元素都小于等于基准元素,右边的子序列中的所有元素都大于基准元素。这个分割操作可以采用多种方式实现,常见的有挖坑法、交换法和指针交替法等。
递归排序:对分割后的两个子序列分别递归地进行快速排序,直到子序列的长度为1或0,即递归的终止条件。
合并操作:将分割后的子序列进行合并,即将左边子序列、基准元素和右边子序列按照顺序拼接起来,得到完整的排序序列。
整个过程可以通过递归来实现,每次递归中选取一个基准元素,将序列分割成两部分,然后递归地对两部分进行排序,最后将结果合并起来得到有序序列。
快速排序的时间复杂度为O(nlogn),其中n为待排序序列的长度。在最坏情况下,快速排序的时间复杂度为O(n^2),但通常情况下快速排序是一种高效的排序算法。快速排序是原地排序的算法,不需要额外的空间。然而,由于快速排序是递归实现的,所以需要使用递归栈空间。
3.2 hoare版本
3.2.1 动图讲解
我们需要定义一个key来指向第一个数,也就是基准元素。
同时定义left和right来指向数组的两端。
我们让right先走,来找比key小的值,找到后left开始走,去找比key大的值,找到之后交换left和right的值,之后继续right找小,left找大,直到两者相遇,循环结束。
这时再把key处的值和left处的值交换,让key走到left位置。
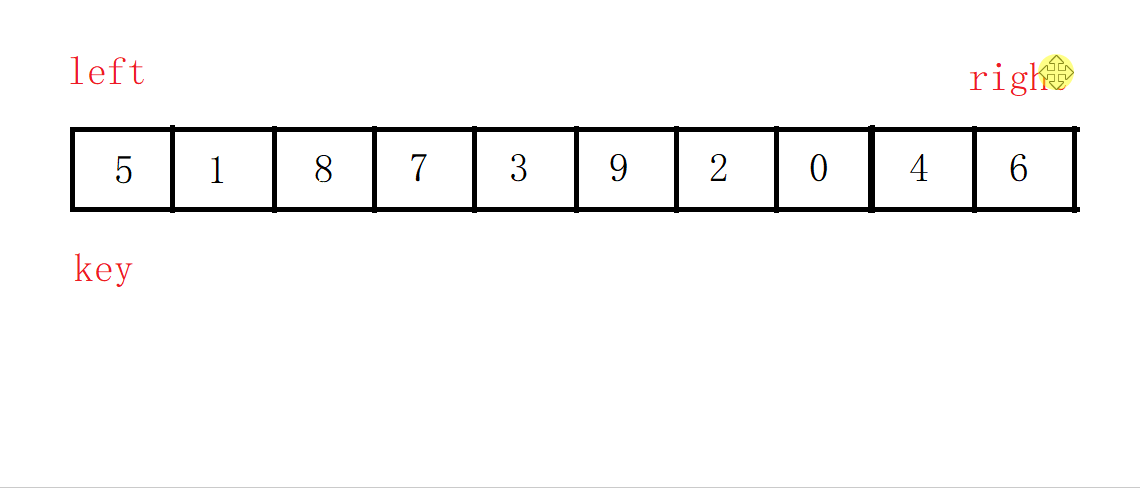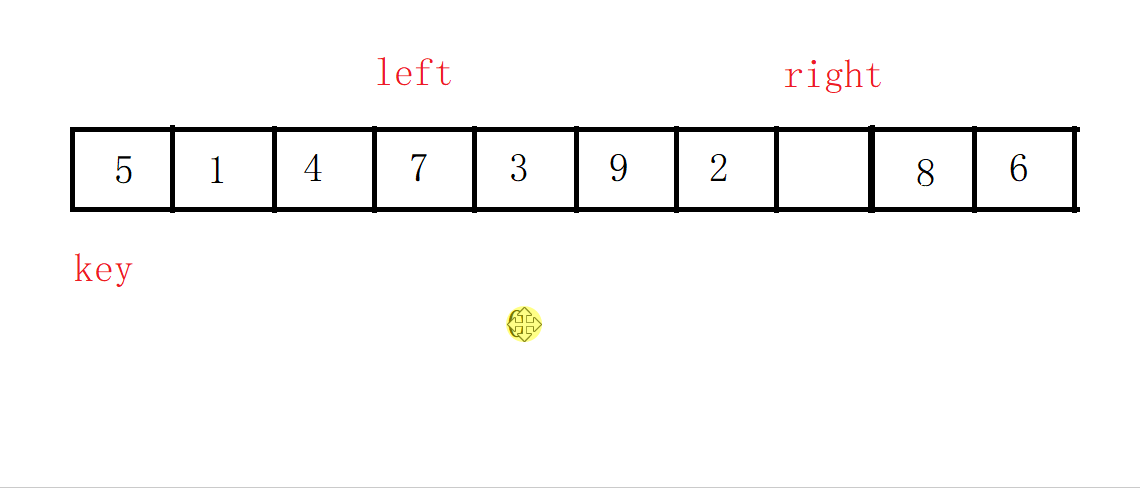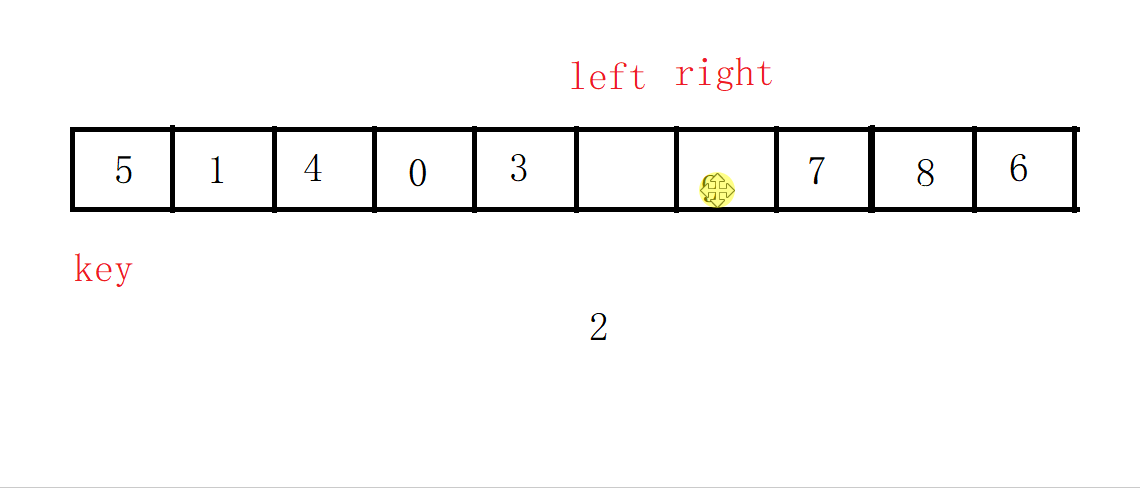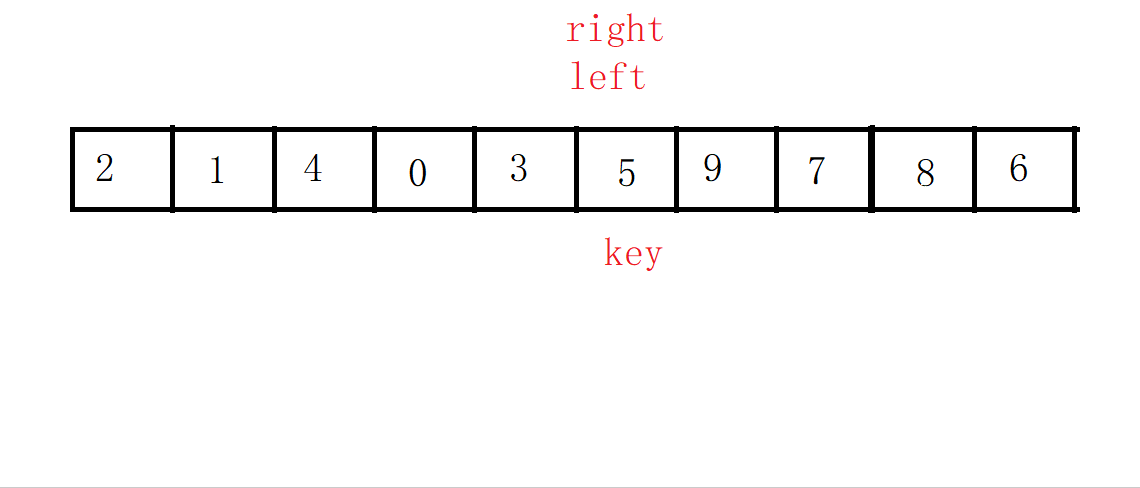
第一次循环结束后如图:
左边的值都比key处的值小,而右边的值都比key处的值大。
这时key所指向的值就是我们上面所说的基准元素。
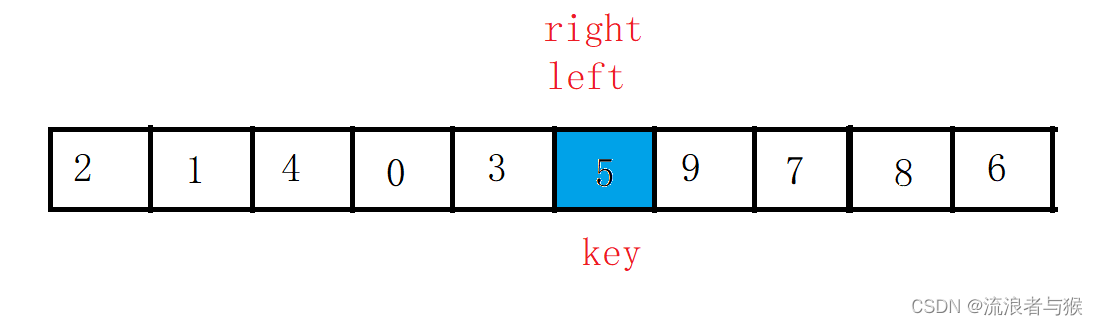
下面我们就需要以key为中点,分为左右两个序列。
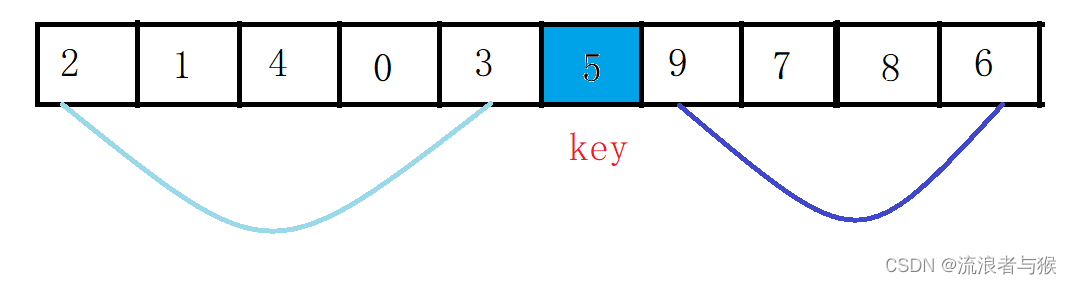
然后我们可以用递归继续调用这个函数,分别把左子序列和右子序列继续排序划分为若干左右子序列,这样就能实现排序。
3.2.2 实现代码
递归结束条件就是当第n个子序列长度为1或者0时结束,也就是子序列起点和尾点重合。
void QuickSort1(int* a, int begin, int end)
{if (begin >= end){return;}int key = begin;int left = begin;int right = end;while (left < right){// 右边先走,找比key值小的while (right > left && a[right] >= a[key]){right--;}// 左边后走,找比key值大的while (right > left && a[left] <= a[key]){left++;}Swap(&a[left], &a[right]);}Swap(&a[key], &a[left]);key = left;//分左右两边//左边QuickSort1(a, begin, key - 1);//右边QuickSort1(a, key + 1, end);
}
void TestQuickSort1()
{int arr[10] = { 5, 1, 8, 7, 3, 9, 2, 0, 4, 6 };int sz = sizeof(arr) / sizeof(arr[0]);QuickSort1(arr, 0, sz - 1);PrintArray(arr, 10);
}
int main()
{TestQuickSort1();return 0;
}
3.2.3 代码优化
如果我们遇到一些极端的情况,比如数组是以排序好或者逆序,这可能就会使我们的时间复杂度大大增加,以及递归调用的太多,可能会导致Stack Overflow的情况。
我们就可以在key,left和right三者中选择一个中位数来当key值。
还有比如数据较少的情况下,选择快排是不大理想的,这时我们用直接插入排序效果会更好。
//优化
int GetMidi(int* a, int begin, int end)
{int midi = (begin + end) / 2;// begin midi end 三个数选中位数if (a[begin] < a[midi]){if (a[midi] < a[end])return midi;else if (a[begin] > a[end])return begin;elsereturn end;}else // a[begin] > a[midi]{if (a[midi] > a[end])return midi;else if (a[begin] < a[end])return begin;elsereturn end;}
}// hoare
void QuickSort1(int* a, int begin, int end)
{if (begin >= end){return;}if (end - begin + 1 <= 10){InsertSort(a + begin, end - begin + 1);}else{int midi = GetMidi(a, begin, end);Swap(&a[midi], &a[begin]);int key = begin;int left = begin;int right = end;while (left < right){// 右边先走,找比key值小的while (right > left && a[right] >= a[key]){right--;}// 左边后走,找比key值大的while (right > left && a[left] <= a[key]){left++;}Swap(&a[left], &a[right]);}Swap(&a[key], &a[left]);key = left;//分左右两边//左边QuickSort1(a, begin, key - 1);//右边QuickSort1(a, key + 1, end);}}
void TestQuickSort1()
{int arr[10] = { 5, 1, 8, 7, 3, 9, 2, 0, 4, 6 };int sz = sizeof(arr) / sizeof(arr[0]);QuickSort1(arr, 0, sz - 1);PrintArray(arr, 10);
}
int main()
{TestQuickSort1();return 0;
}
3.3 挖坑法
3.3.1 动图详解
挖坑法与hoare版本的快排并无太大差别。
我们另定义一个hole变量,left和right不变,这时的key不再是下标,而是一个具体的数值,key是首元素的值。
我们仍旧是右边先找小,找到之后并不是直接让左边去找大,而是让这个小的值赋值给hole的位置,注意不是交换,key的值记录着最开始的hole位置的值,不必担心丢失。
接着让hole移动到right位置,左边开始找大,找到后也是把left指向的值赋值给hole位置,hole移动到left位置。
仍旧是left和right相遇之后,把key记录的值赋值给hole位置。

3.3.2实现代码
//挖坑法
void QuickSort2(int* a, int begin, int end)
{if (begin >= end){return;}int midi = GetMidi(a, begin, end);Swap(&a[midi], &a[begin]);int left = begin;int right = end;int hole = left;int key = a[hole];while (left < right){while (a[right] >= key && right > left){right--;}a[hole] = a[right];hole = right;while (a[left] <= key && right > left){left++;}a[hole] = a[left];hole = left;}a[hole] = key;QuickSort2(a, begin, hole - 1);QuickSort2(a, hole + 1, end);
}void TestQuickSort2()
{int arr[10] = { 5, 1, 8, 7, 3, 9, 2, 0, 4, 6 };int sz = sizeof(arr) / sizeof(arr[0]);QuickSort2(arr, 0, sz - 1);PrintArray(arr, 10);
}
int main()
{TestQuickSort2();return 0;
}
3.4 双指针
3.4.1 动图详解
双指针相对于上面两个代码是相较少的,不必再去三位取中。
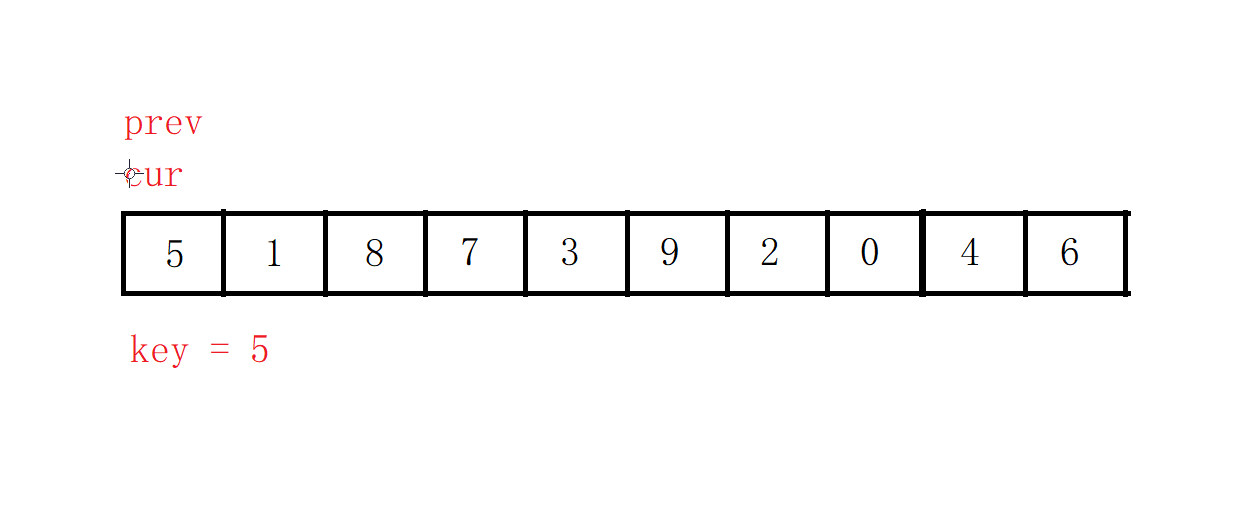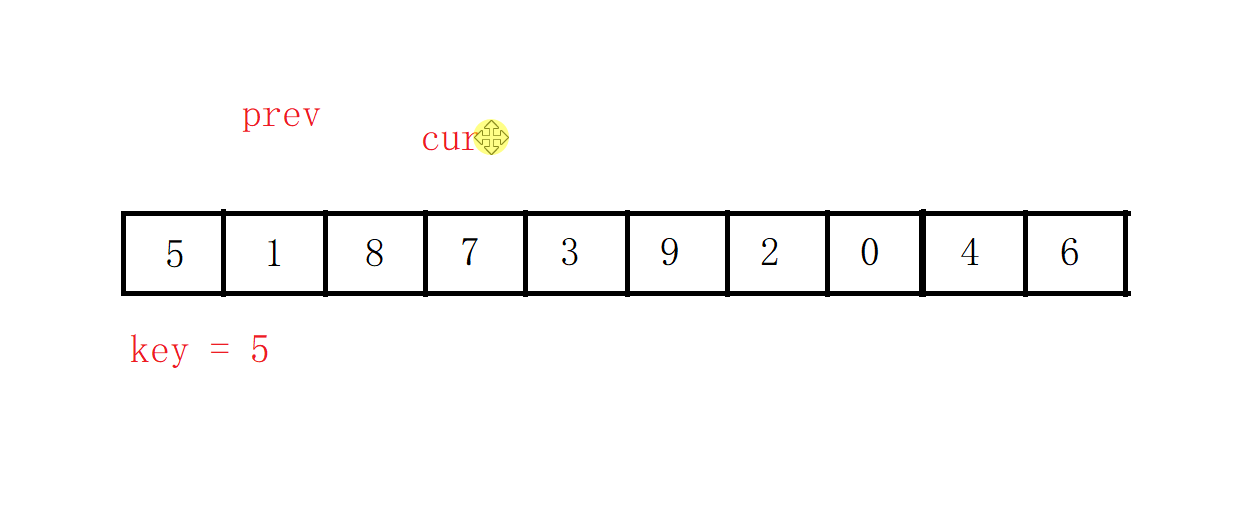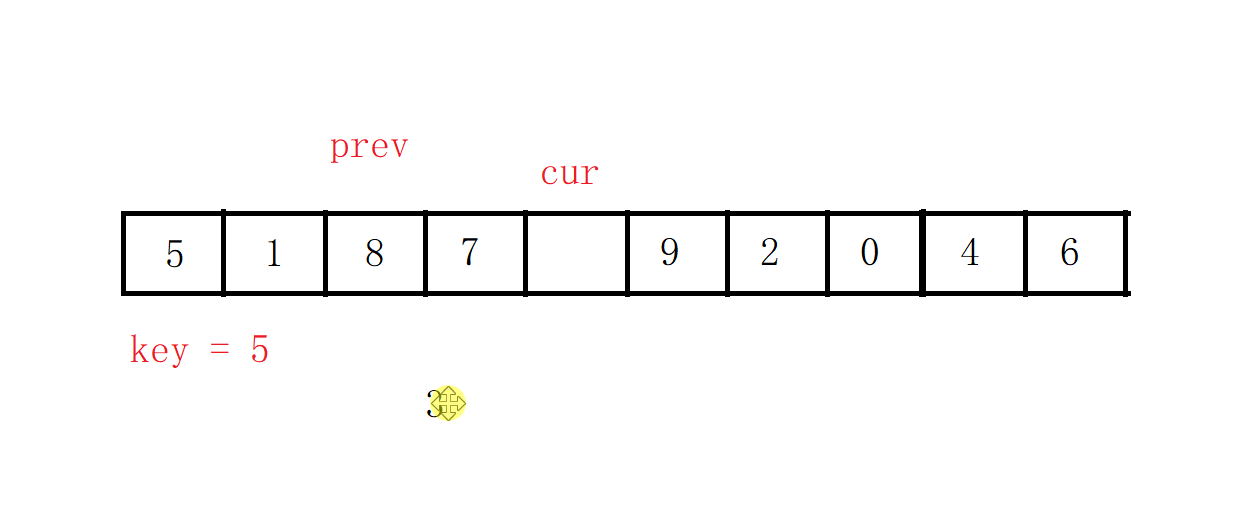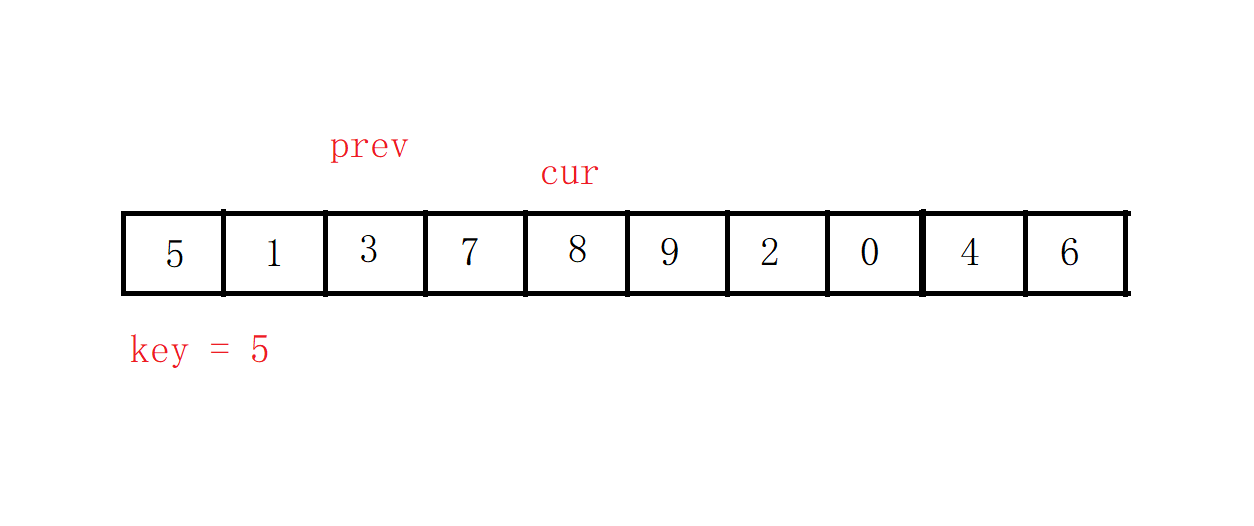
定义两个指针cur,prev,而key仍然是值。
开始的时候两个指针都指向第一个元素
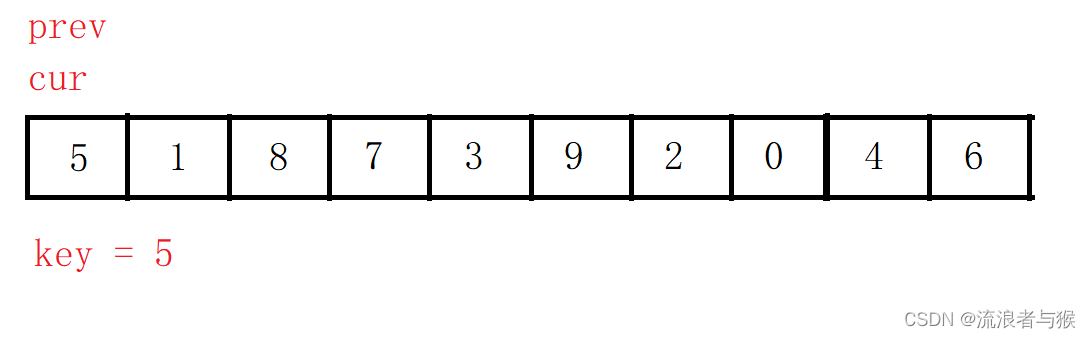
之后cur先走,找比key值小的数,找到之后,prev向前走一步,如果这时prev和cur的指向的不是同一个元素,就交换两者指向的值。
反之,如果两者重叠,cur则继续往前走一步。
直到cur出了数组,循环结束,这时再交换key值和prev。
再以prev为中心,分为左右子序列。
3.4.2 实现代码
// 双指针
void QuickSort3(int* a, int begin, int end)
{if (begin >= end){return;}int key = begin;int prev = begin;int cur = prev + 1;while (cur <= end){if (a[cur] < a[key] && ++prev != cur){Swap(&a[cur], &a[prev]);}cur++;}Swap(&a[key], &a[prev]);QuickSort3(a, begin, prev - 1);QuickSort3(a, prev + 1, end);
}
void TestQuickSort3()
{int arr[10] = { 5, 1, 8, 7, 3, 9, 2, 0, 4, 6 };int sz = sizeof(arr) / sizeof(arr[0]);QuickSort3(arr, 0, sz - 1);PrintArray(arr, 10);
}
int main()
{TestQuickSort3();return 0;
}
4. 无递归实现快排
4.1 基本思想
非递归实现快速排序算法的关键是使用栈来模拟递归过程。具体步骤如下:
- 创建一个栈,并将待排序数组的起始索引和结束索引入栈。
- 循环直到栈为空:
- 弹出栈顶的起始索引和结束索引,作为当前子数组的范围。
- 选择一个基准元素,将数组按照基准元素进行划分,得到基准元素的索引。
- 如果基准元素左侧的子数组长度大于1,则将左侧子数组的起始索引和结束索引入栈。
- 如果基准元素右侧的子数组长度大于1,则将右侧子数组的起始索引和结束索引入栈。
- 返回排序后的数组。
4.2 实现代码
前面我们都是用递归的方法来实现快排的,思考一下不用递归该怎么写。
这里我们可以用栈来实现,我们每次把需要排列的左右子序列的开始和结束的下标入栈,记录范围,之后再出栈赋给left和right,又或者其它变量,最后调用上面的函数来实现排序。
我们先来看代码,后面来具体分析。
在这里的栈,我还是调用之前写的栈代码,感兴趣的小伙伴可以看数据结构的专栏。
// hoare
int PartSort1(int* a, int begin, int end)
{int midi = GetMidi(a, begin, end);Swap(&a[midi], &a[begin]);int left = begin, right = end;int keyi = begin;while (left < right){// 右边找小while (left < right && a[right] >= a[keyi]){--right;}// 左边找大while (left < right && a[left] <= a[keyi]){++left;}Swap(&a[left], &a[right]);}Swap(&a[left], &a[keyi]);return left;
}
//挖坑法
int PartSort2(int* a, int begin, int end)
{int midi = GetMidi(a, begin, end);Swap(&a[midi], &a[begin]);int left = begin;int right = end;int hole = left;int key = a[hole];while (left < right){while (a[right] >= key && right > left){right--;}a[hole] = a[right];hole = right;while (a[left] <= key && right > left){left++;}a[hole] = a[left];hole = left;}a[hole] = key;return hole;
}
//双指针
int PartSort3(int* a, int begin, int end)
{int midi = GetMidi(a, begin, end);Swap(&a[midi], &a[begin]);int key = begin;int prev = begin;int cur = prev + 1;while (cur <= end){if (a[cur] < a[key] && ++prev != cur){Swap(&a[cur], &a[prev]);}cur++;}Swap(&a[key], &a[prev]);key = prev;return key;
}
//无递归方法实现
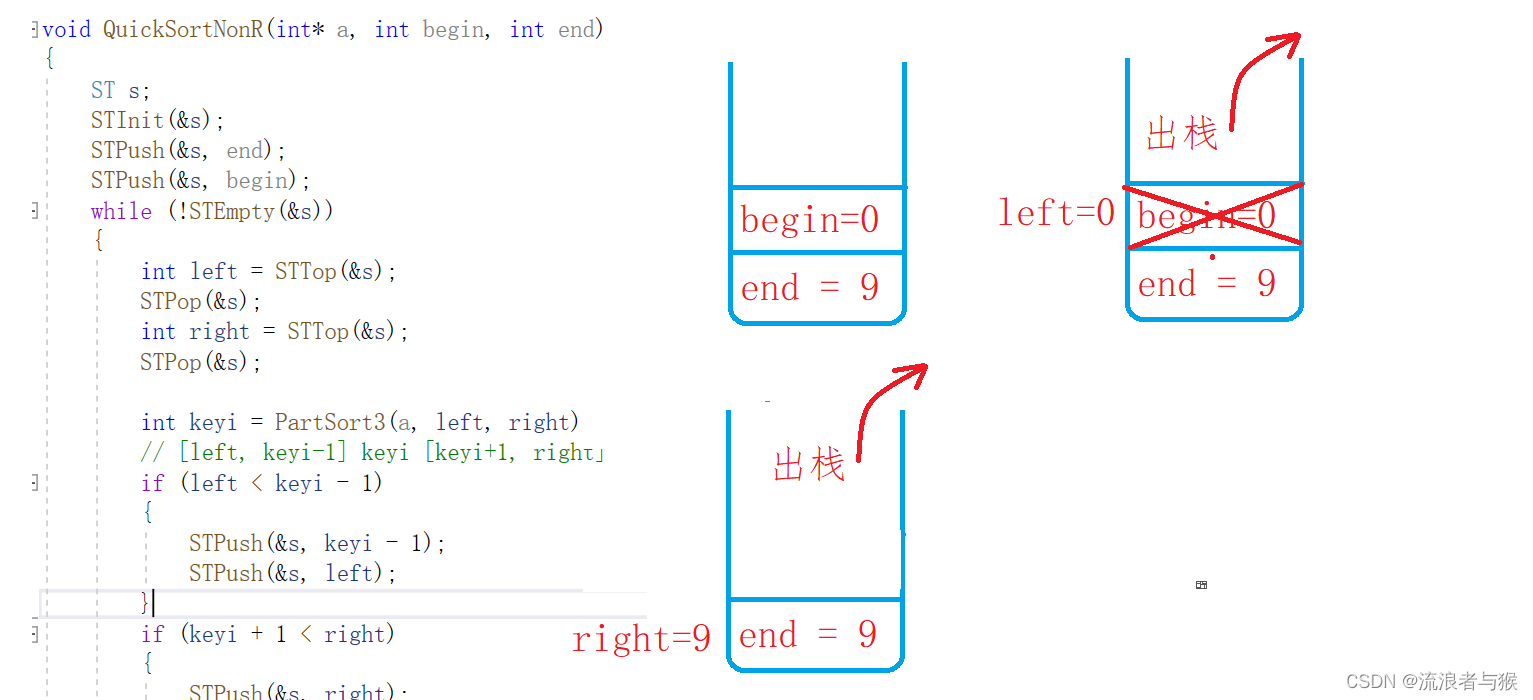
void QuickSortNonR(int* a, int begin, int end)
{ST s;STInit(&s);STPush(&s, end);STPush(&s, begin);while (!STEmpty(&s)){int left = STTop(&s);STPop(&s);int right = STTop(&s);STPop(&s);int keyi = PartSort3(a, left, right);// [left, keyi-1] keyi [keyi+1, right]if (left < keyi - 1){STPush(&s, keyi - 1);STPush(&s, left);}if (keyi + 1 < right){STPush(&s, right);STPush(&s, keyi + 1);}}STDestroy(&s);
}
相关文章:

【C语言】数据结构——排序二(快排)
💗个人主页💗 ⭐个人专栏——数据结构学习⭐ 💫点击关注🤩一起学习C语言💯💫 目录 导读:数组打印与交换1. 交换排序1.1 基本思想:1.2 冒泡与快排的异同 2. 冒泡排序2.1 基本思想2.2 …...
企业私有云容器化架构
什么是虚拟化: 虚拟化(Virtualization)技术最早出现在 20 世纪 60 年代的 IBM 大型机系统,在70年代的 System 370 系列中逐渐流行起来,这些机器通过一种叫虚拟机监控器(Virtual Machine Monitor,VMM&#x…...
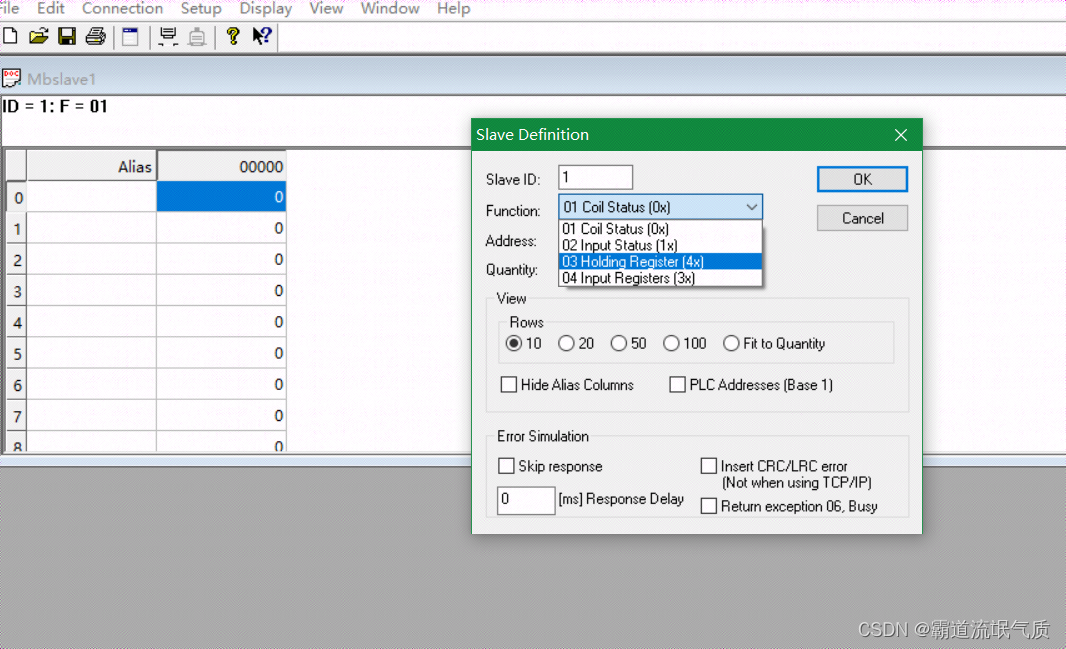
SpringBoot+modbus4j实现ModebusTCP通讯读取数据
场景 Windows上ModbusTCP模拟Master与Slave工具的使用: Windows上ModbusTCP模拟Master与Slave工具的使用-CSDN博客 Modebus TCP Modbus由MODICON公司于1979年开发,是一种工业现场总线协议标准。 1996年施耐德公司推出基于以太网TCP/IP的Modbus协议&…...

Linux性能优化全景指南
Part1 Linux性能优化 1、性能优化性能指标 高并发和响应快对应着性能优化的两个核心指标:吞吐和延时 应用负载角度:直接影响了产品终端的用户体验系统资源角度:资源使用率、饱和度等 性能问题的本质就是系统资源已经到达瓶颈,但…...
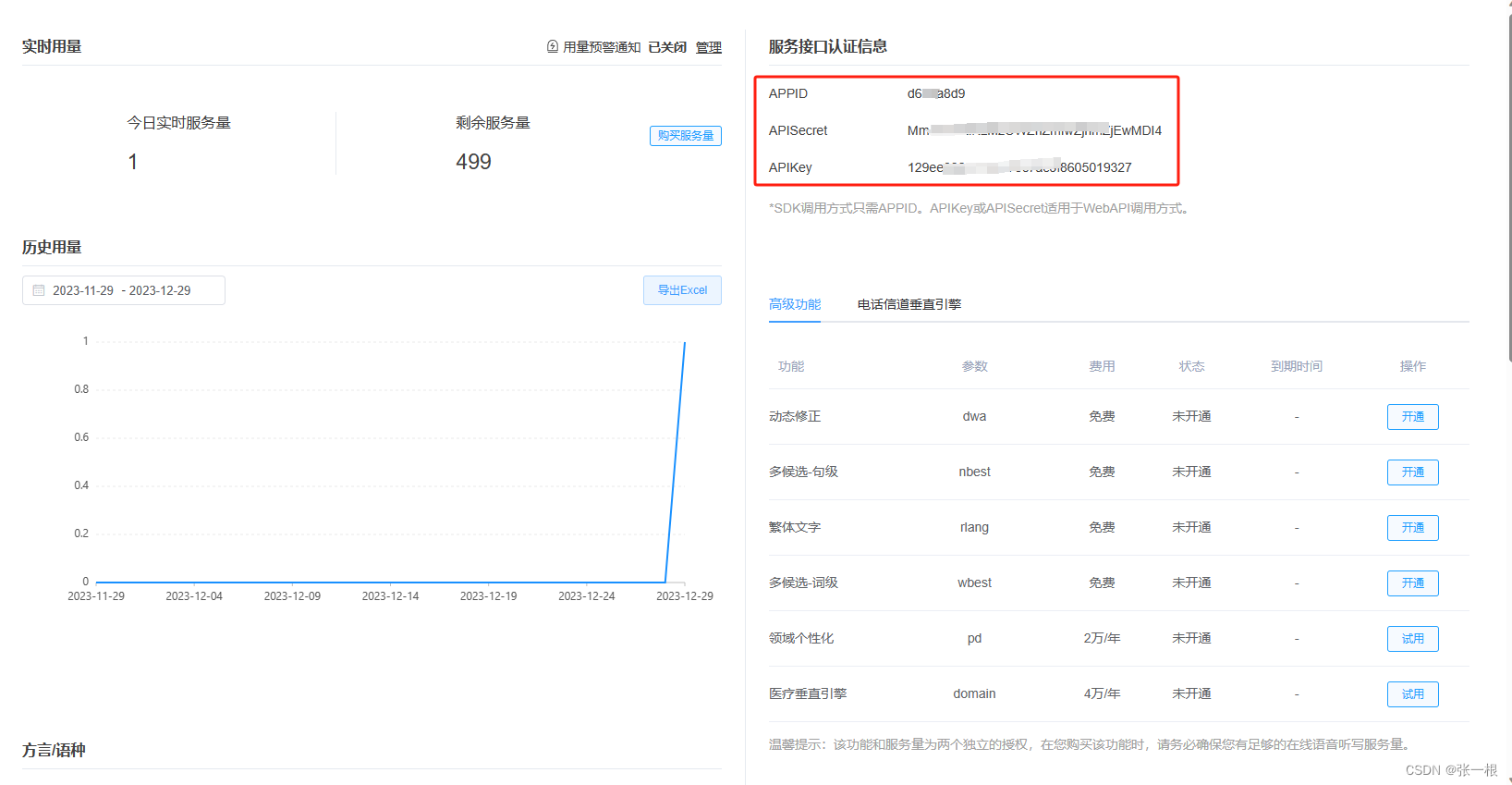
树莓派 ubuntu20.04下 python调讯飞的语音API,语音识别和语音合成
目录 1.环境搭建2.去讯飞官网申请密钥3.语音识别(sst)4.语音合成(tts)5.USB声卡可能报错 1.环境搭建 #环境说明:(尽量在ubuntu下使用, 本次代码均在该环境下实现) sudo apt-get install sox # 安装语音播放软件 pip …...
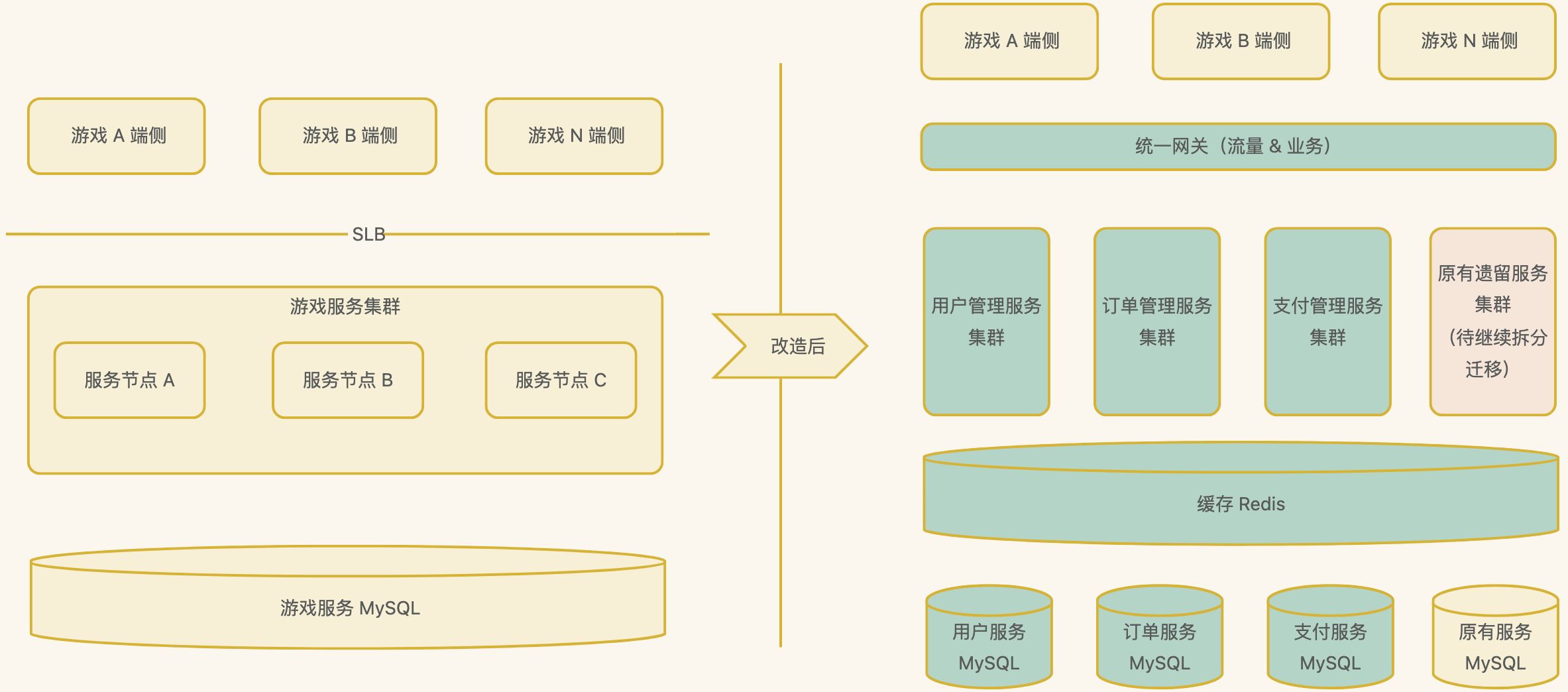
分布式系统架构设计之分布式系统实践案例和未来展望
分布式系统在过去的几十年里经历了长足的发展,从最初的简单分布式架构到今天的微服务、云原生等先进架构,取得了丰硕的成果。本文将通过实际案例分享分布式系统的架构实践,并展望未来可能的发展方向。 一、实践案例 1、微服务化实践 背景 …...
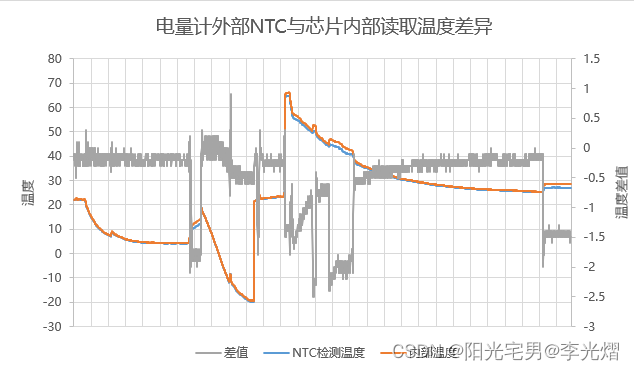
【办公软件】Excel双坐标轴图表
在工作中整理测试数据,往往需要一个图表展示两个差异较大的指标。比如共有三个数据,其中两个是要进行对比的温度值,另一个指标是两个温度的差值,这个差值可能很小。 举个实际的例子:数据如下所示,NTC检测温…...

彻底理解前端安全面试题(1)—— XSS 攻击,3种XSS攻击详解,建议收藏(含源码)
前言 前端关于网络安全看似高深莫测,其实来来回回就那么点东西,我总结一下就是 3 1 4,3个用字母描述的【分别是 XSS、CSRF、CORS】 一个中间人攻击。当然 CORS 同源策略是为了防止攻击的安全策略,其他的都是网络攻击。除了这…...

UE5.1_AI随机漫游
UE5.1_AI随机漫游 目录 UE5.1_AI随机漫游 AI随机漫游方法 方法1:AI角色蓝图直接写方法...
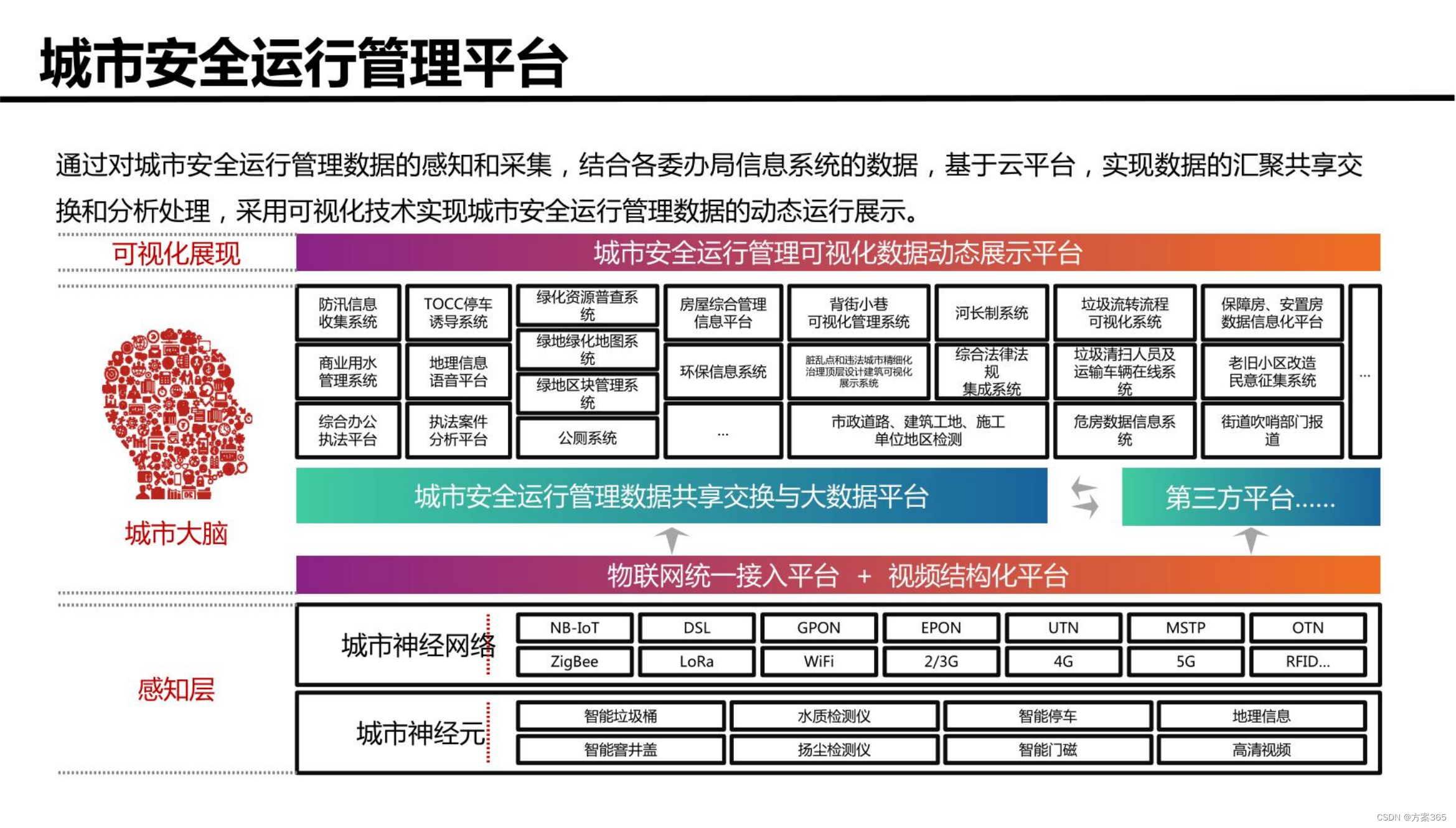
智慧城市新型基础设施建设综合方案:文件全文52页,附下载
关键词:智慧城市建设方案,智慧城市发展的前景和趋势,智慧城市项目方案,智慧城市管理平台,数字化城市,城市数字化转型 一、智慧城市新基建建设背景 1、城市化进程加速:随着城市化进程的加速&am…...
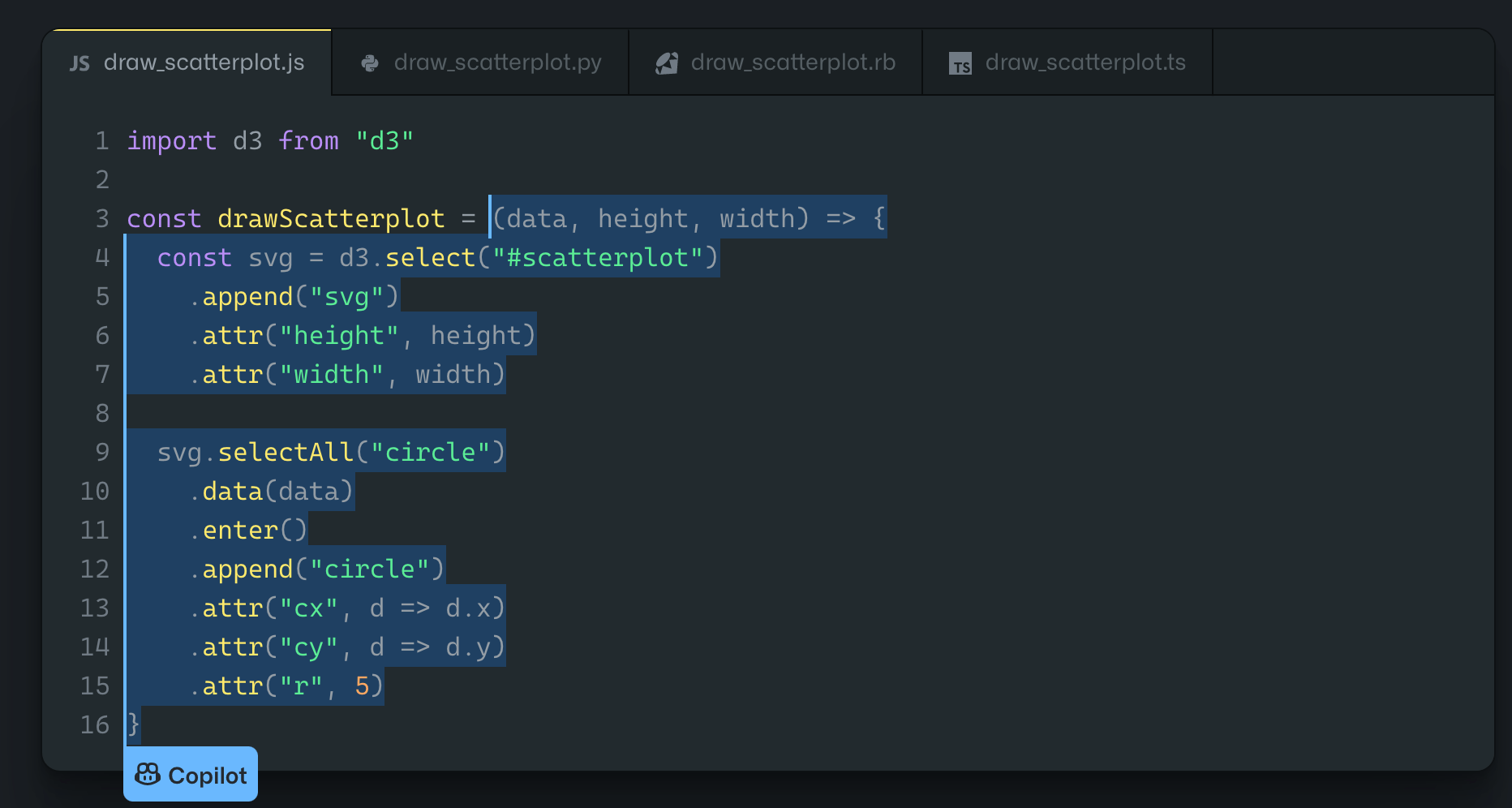
GitHub Copilot 终极详细介绍
编写代码通常是一项乏味且耗时的任务。现代开发人员一直在寻找新的方法来提高编程的生产力、准确性和效率。 像 GitHub Copilot 这样的自动代码生成工具可以使这成为可能。 GitHub Copilot 到底是什么? GitHub Copilot 于 2021 年 10 月推出,是 GitHub 的…...

LeetCode第63题 - 不同路径 II
题目 解答 class Solution {public int uniquePathsWithObstacles(int[][] obstacleGrid) {int m obstacleGrid.length;int n obstacleGrid[0].length;if (obstacleGrid[0][0] 1) {return 0;}if (obstacleGrid[m - 1][n - 1] 1) {return 0;}int[][] dp new int[m][n];dp…...
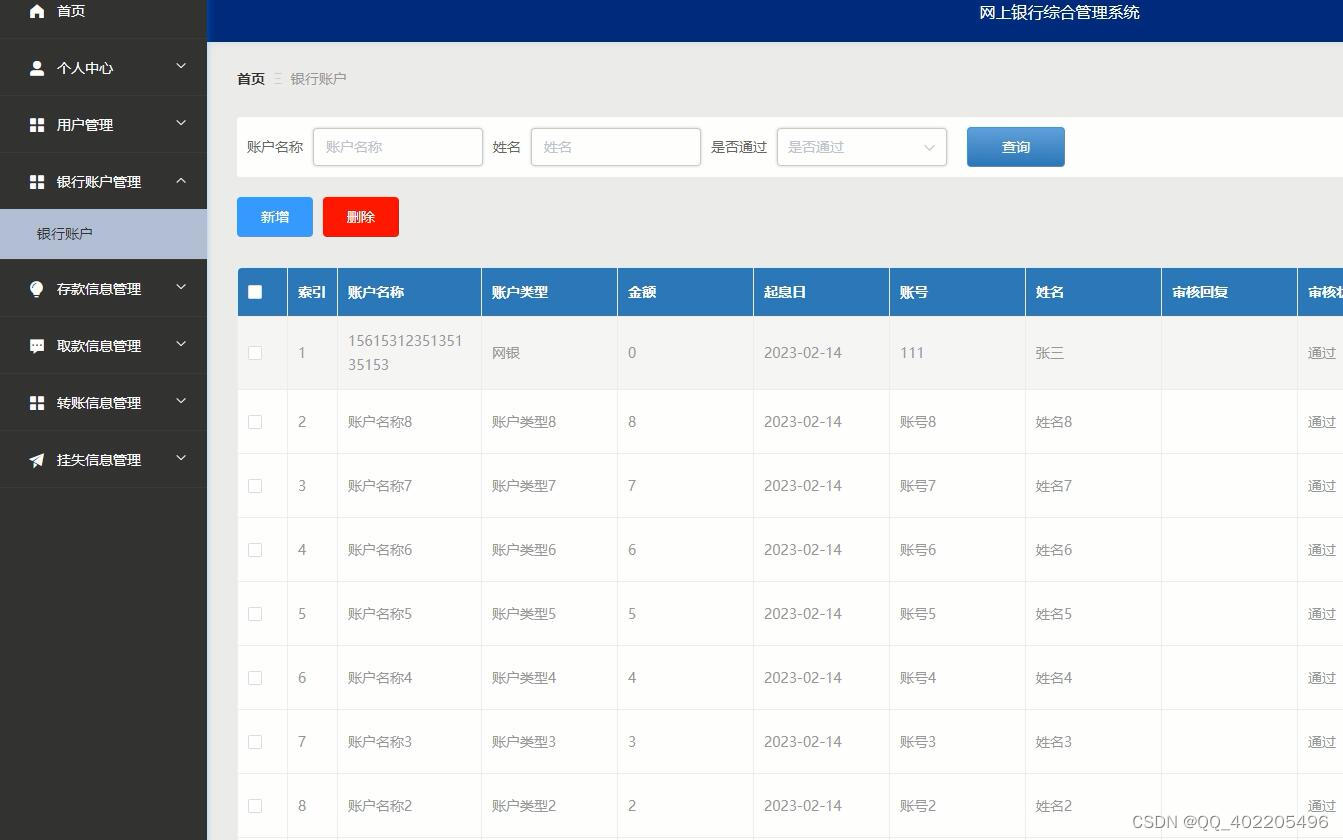
python+django网上银行业务综合管理系统vue_bvj8b
本课题主要研究如何用信息化技术改善传统网上银行综合管理行业的经营和管理模式,简化网上银行综合管理的难度,根据管理实际业务需求,调研、分析和编写系统需求文档,设计编写符合银行需要的系统说明书,绘制数据库结构模…...

【软件工程】走进瀑布模型:传统软件开发的经典之路
🍎个人博客:个人主页 🏆个人专栏: 软件工程 ⛳️ 功不唐捐,玉汝于成 目录 前言: 正文 主要阶段: 优点: 缺点: 应用范围: 结语 我的其他博客 前言&am…...
C卷 (JavaPythonNode.jsC语言C++))
两个字符串间的最短路径问题 (100%用例)C卷 (JavaPythonNode.jsC语言C++)
给定两个字符串,分别为字符串A与字符串B。例如A字符串为ABCABBA,B字符串为CBABAC可以得到下图m*n的二维数组,定义原点为(0,0),终点为(m,n),水平与垂直的每一条边距离为1,映射成坐标系如下图 从原点(0,0)到(0,A)为水平边,距离为1,从(0,A)到(A,C)为垂直边,距离为1;假设两…...

通过ADB来实现脚本来控制手机
ADB 简介 adb的全称为Android Debug Bridge,安卓调试桥,可以通过调试命令来控制手机,诸如开机,关机等按键控制;或者启动,关闭应用;异或进行触摸模拟. 通过学习adb,可以实现简单的脚本控制,最大的特点是不需要root,对于普通手机都可以进行,帮助我们完成一些简单的重复性事件,…...
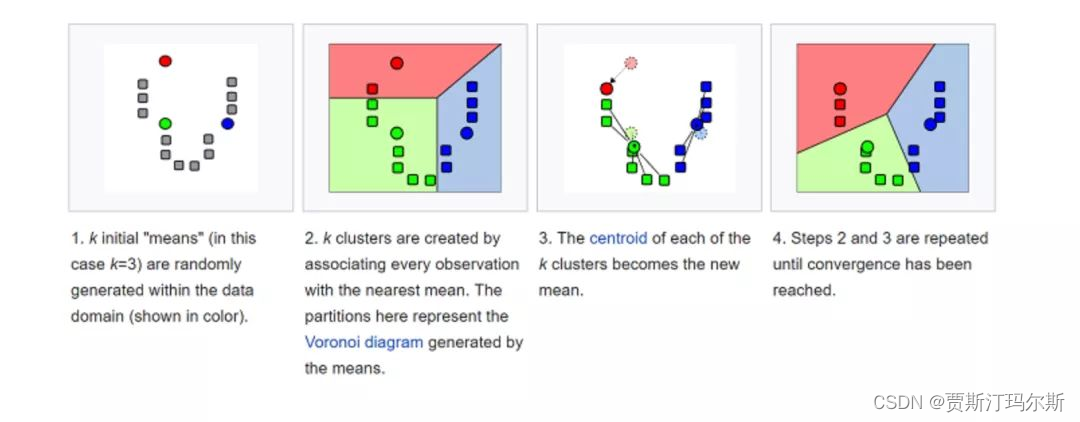
机器学习之K-means聚类
概念 K-means是一种常用的机器学习算法,用于聚类分析。聚类是一种无监督学习方法,它试图将数据集中的样本划分为具有相似特征的组(簇)。K-means算法的目标是将数据集划分为K个簇,其中每个样本属于与其最近的簇中心。 以下是K-means算法的基本步骤: 选择簇的数量(K值)…...

SSH 端口转发:如何将服务绑定到本地 IP 地址
在日常工作中,我们经常需要访问位于远程服务器上的服务,如数据库、Web 应用程序或其他类型的服务器。直接访问这些服务可能会因为安全限制或网络配置而变得复杂或不可能。这时,SSH 端口转发就成了我们的得力助手。在本篇博客中,我…...
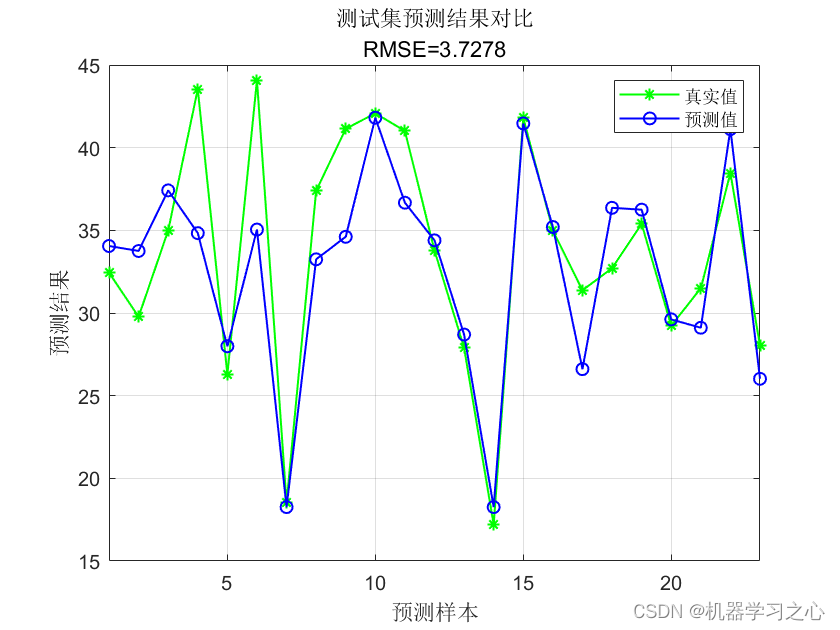
回归预测 | MATLAB实ZOA-LSTM基于斑马优化算法优化长短期记忆神经网络的多输入单输出数据回归预测模型 (多指标,多图)
回归预测 | MATLAB实ZOA-LSTM基于斑马优化算法优化长短期记忆神经网络的多输入单输出数据回归预测模型 (多指标,多图) 目录 回归预测 | MATLAB实ZOA-LSTM基于斑马优化算法优化长短期记忆神经网络的多输入单输出数据回归预测模型 (…...
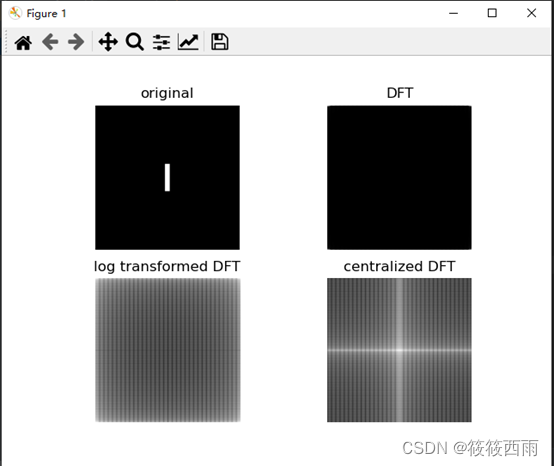
python实现图像的二维傅里叶变换——冈萨雷斯数字图像处理
原理 二维傅里叶变换是一种在图像处理中常用的数学工具,它将图像从空间域(我们通常看到的像素排列)转换到频率域。这种变换揭示了图像的频率成分,有助于进行各种图像分析和处理,如滤波、图像增强、边缘检测等。 在数学…...

铭豹扩展坞 USB转网口 突然无法识别解决方法
当 USB 转网口扩展坞在一台笔记本上无法识别,但在其他电脑上正常工作时,问题通常出在笔记本自身或其与扩展坞的兼容性上。以下是系统化的定位思路和排查步骤,帮助你快速找到故障原因: 背景: 一个M-pard(铭豹)扩展坞的网卡突然无法识别了,扩展出来的三个USB接口正常。…...

挑战杯推荐项目
“人工智能”创意赛 - 智能艺术创作助手:借助大模型技术,开发能根据用户输入的主题、风格等要求,生成绘画、音乐、文学作品等多种形式艺术创作灵感或初稿的应用,帮助艺术家和创意爱好者激发创意、提高创作效率。 - 个性化梦境…...

19c补丁后oracle属主变化,导致不能识别磁盘组
补丁后服务器重启,数据库再次无法启动 ORA01017: invalid username/password; logon denied Oracle 19c 在打上 19.23 或以上补丁版本后,存在与用户组权限相关的问题。具体表现为,Oracle 实例的运行用户(oracle)和集…...
: K8s 核心概念白话解读(上):Pod 和 Deployment 究竟是什么?)
云原生核心技术 (7/12): K8s 核心概念白话解读(上):Pod 和 Deployment 究竟是什么?
大家好,欢迎来到《云原生核心技术》系列的第七篇! 在上一篇,我们成功地使用 Minikube 或 kind 在自己的电脑上搭建起了一个迷你但功能完备的 Kubernetes 集群。现在,我们就像一个拥有了一块崭新数字土地的农场主,是时…...

RocketMQ延迟消息机制
两种延迟消息 RocketMQ中提供了两种延迟消息机制 指定固定的延迟级别 通过在Message中设定一个MessageDelayLevel参数,对应18个预设的延迟级别指定时间点的延迟级别 通过在Message中设定一个DeliverTimeMS指定一个Long类型表示的具体时间点。到了时间点后…...

【入坑系列】TiDB 强制索引在不同库下不生效问题
文章目录 背景SQL 优化情况线上SQL运行情况分析怀疑1:执行计划绑定问题?尝试:SHOW WARNINGS 查看警告探索 TiDB 的 USE_INDEX 写法Hint 不生效问题排查解决参考背景 项目中使用 TiDB 数据库,并对 SQL 进行优化了,添加了强制索引。 UAT 环境已经生效,但 PROD 环境强制索…...

无法与IP建立连接,未能下载VSCode服务器
如题,在远程连接服务器的时候突然遇到了这个提示。 查阅了一圈,发现是VSCode版本自动更新惹的祸!!! 在VSCode的帮助->关于这里发现前几天VSCode自动更新了,我的版本号变成了1.100.3 才导致了远程连接出…...

电脑插入多块移动硬盘后经常出现卡顿和蓝屏
当电脑在插入多块移动硬盘后频繁出现卡顿和蓝屏问题时,可能涉及硬件资源冲突、驱动兼容性、供电不足或系统设置等多方面原因。以下是逐步排查和解决方案: 1. 检查电源供电问题 问题原因:多块移动硬盘同时运行可能导致USB接口供电不足&#x…...

WordPress插件:AI多语言写作与智能配图、免费AI模型、SEO文章生成
厌倦手动写WordPress文章?AI自动生成,效率提升10倍! 支持多语言、自动配图、定时发布,让内容创作更轻松! AI内容生成 → 不想每天写文章?AI一键生成高质量内容!多语言支持 → 跨境电商必备&am…...

前端开发面试题总结-JavaScript篇(一)
文章目录 JavaScript高频问答一、作用域与闭包1.什么是闭包(Closure)?闭包有什么应用场景和潜在问题?2.解释 JavaScript 的作用域链(Scope Chain) 二、原型与继承3.原型链是什么?如何实现继承&a…...
