当前位置： 首页 > news >正文

证明：切线垂直于半径

news 2026/2/10 14:03:17

证明：

切线垂直于过切点的半径。

下面是网上最简单的证明方法。

证明：
利用反证法。
如下图所示，直线AB和圆O切于点A，假设OA 不垂直于 AB，而 O B ⊥ A B OB \perp AB OB⊥AB，则 ∠ O B A = 90 ° \angle OBA = 90 \degree ∠OBA=90°，根据勾股定理可得斜边最长，即边OA>边OB ，但是实际上直线和圆的交点只有一个交点A，OA是半径而OB应该比半径长，因而假设不成立。

在这里插入图片描述

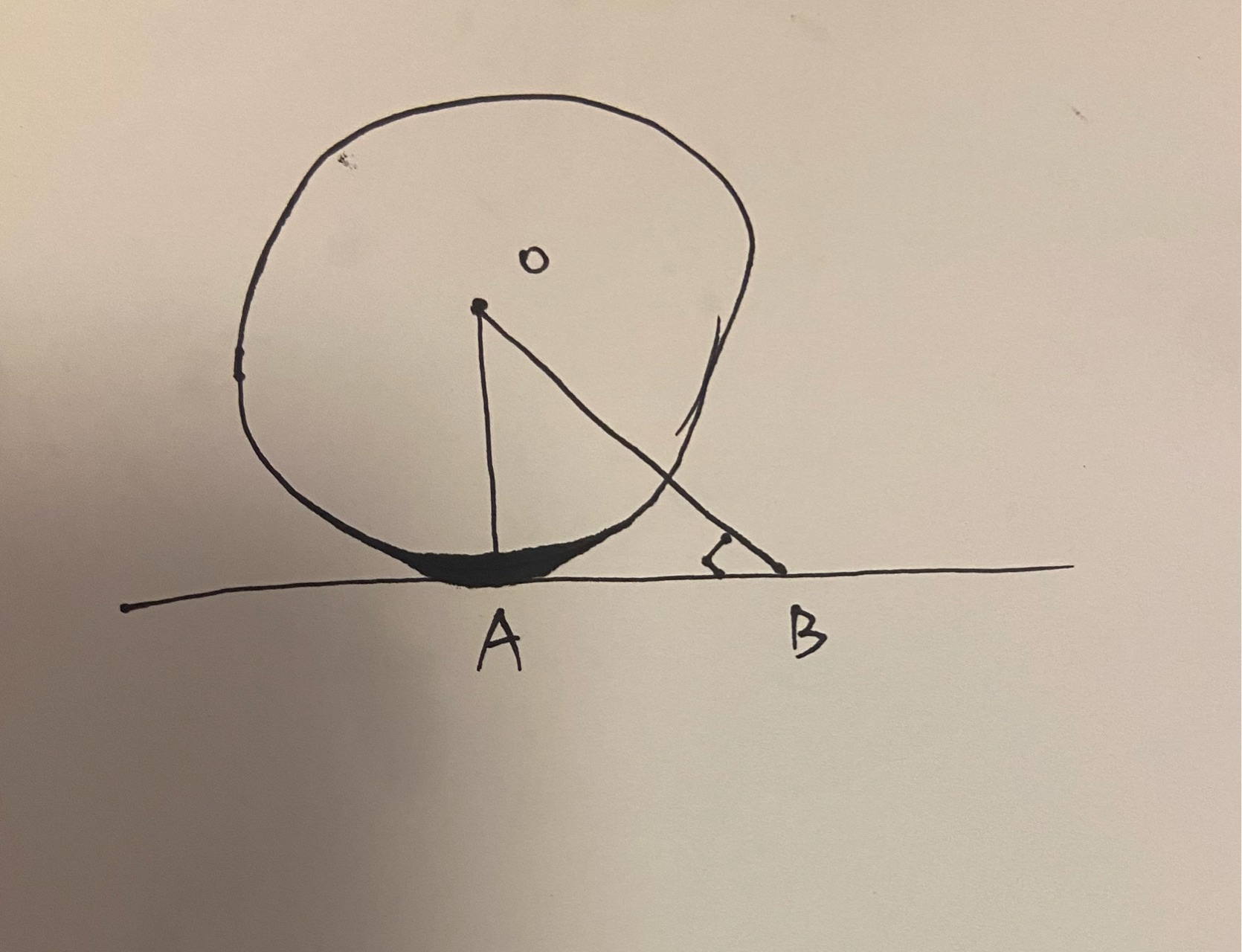
相关文章：

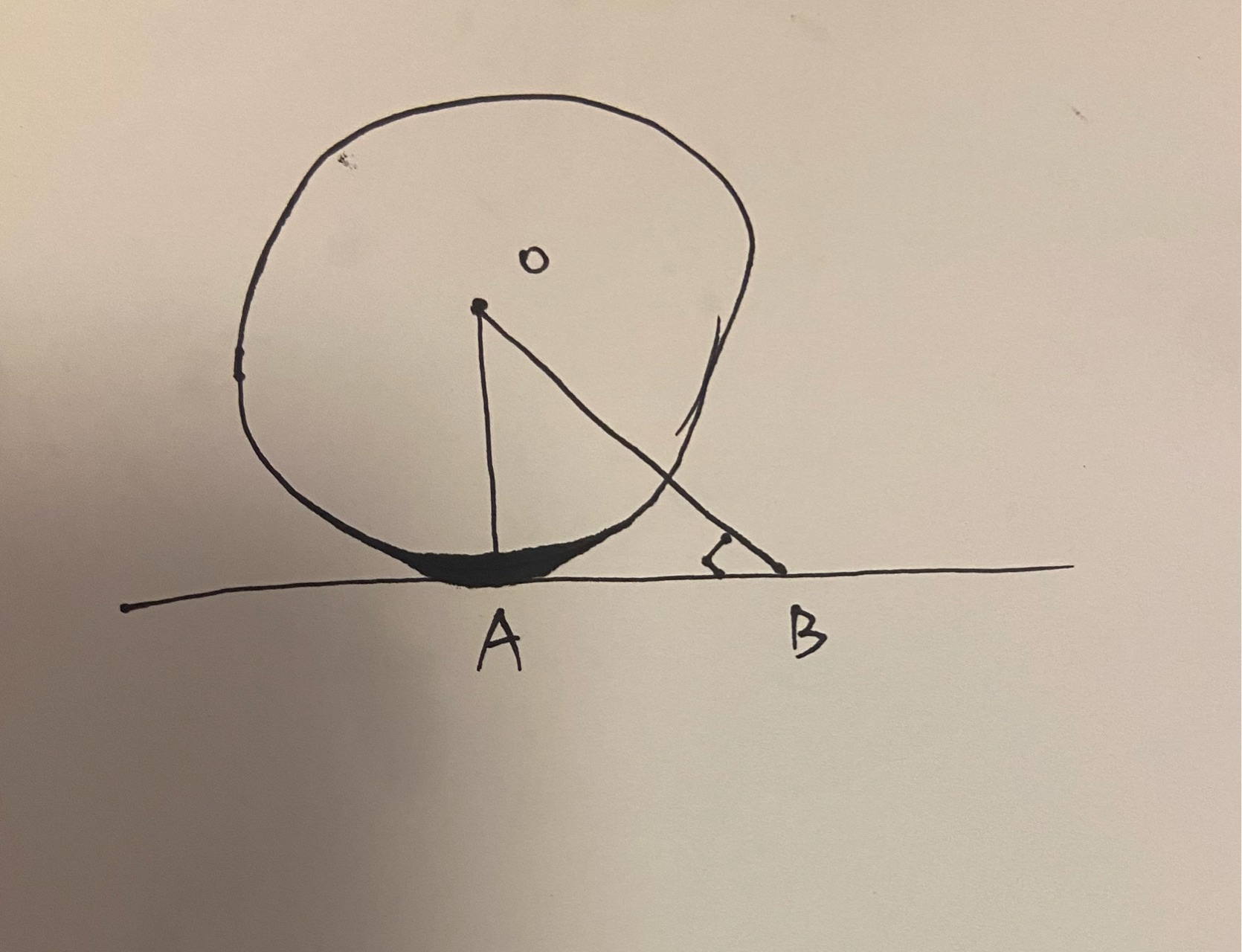
证明：切线垂直于半径

证明： 切线垂直于过切点的半径。 下面是网上最简单的证明方法。 证明： 利用反证法。 如下图所示，直线AB和圆O切于点A，假设OA 不垂直于 AB，而 O B ⊥ A B OB \perp AB OB⊥AB，则 ∠ O B A 90 \angle OB…...

编程日记 2023/12/31 15:02:46

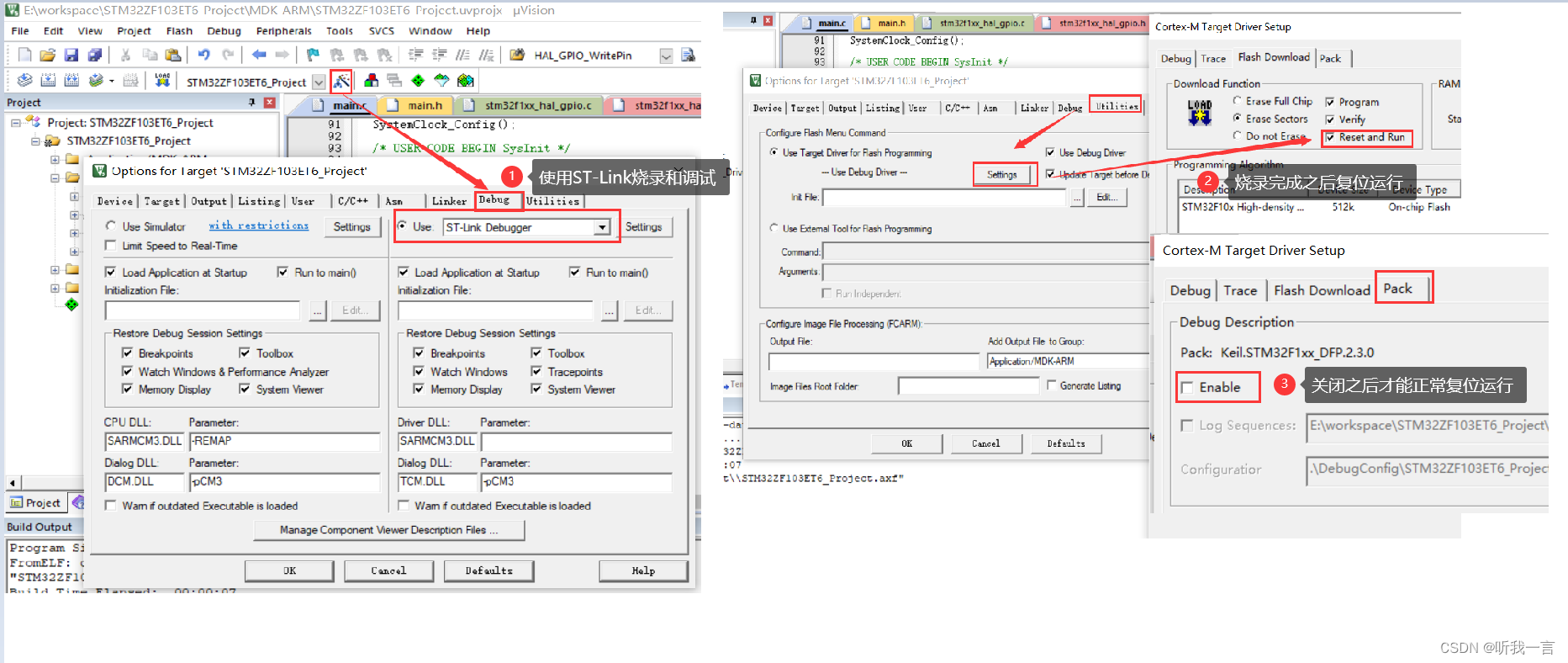
普中STM32-PZ6806L开发板(STM32CubeMX创建项目并点亮LED灯)

简介 搭建一个用于驱动 STM32F103ZET6 GPIO点亮LED灯的任务;电路原理图 LED电路原理图 芯片引脚连接LED驱动引脚原理图 创建一个点亮LED灯的Keil 5项目 创建STM32CubeMX项目 New Project -> 单击 -> 芯片搜索STM32F103ZET6->双击创建 初始化时钟 调试设置 一…...

编程日记 2023/12/31 15:00:44

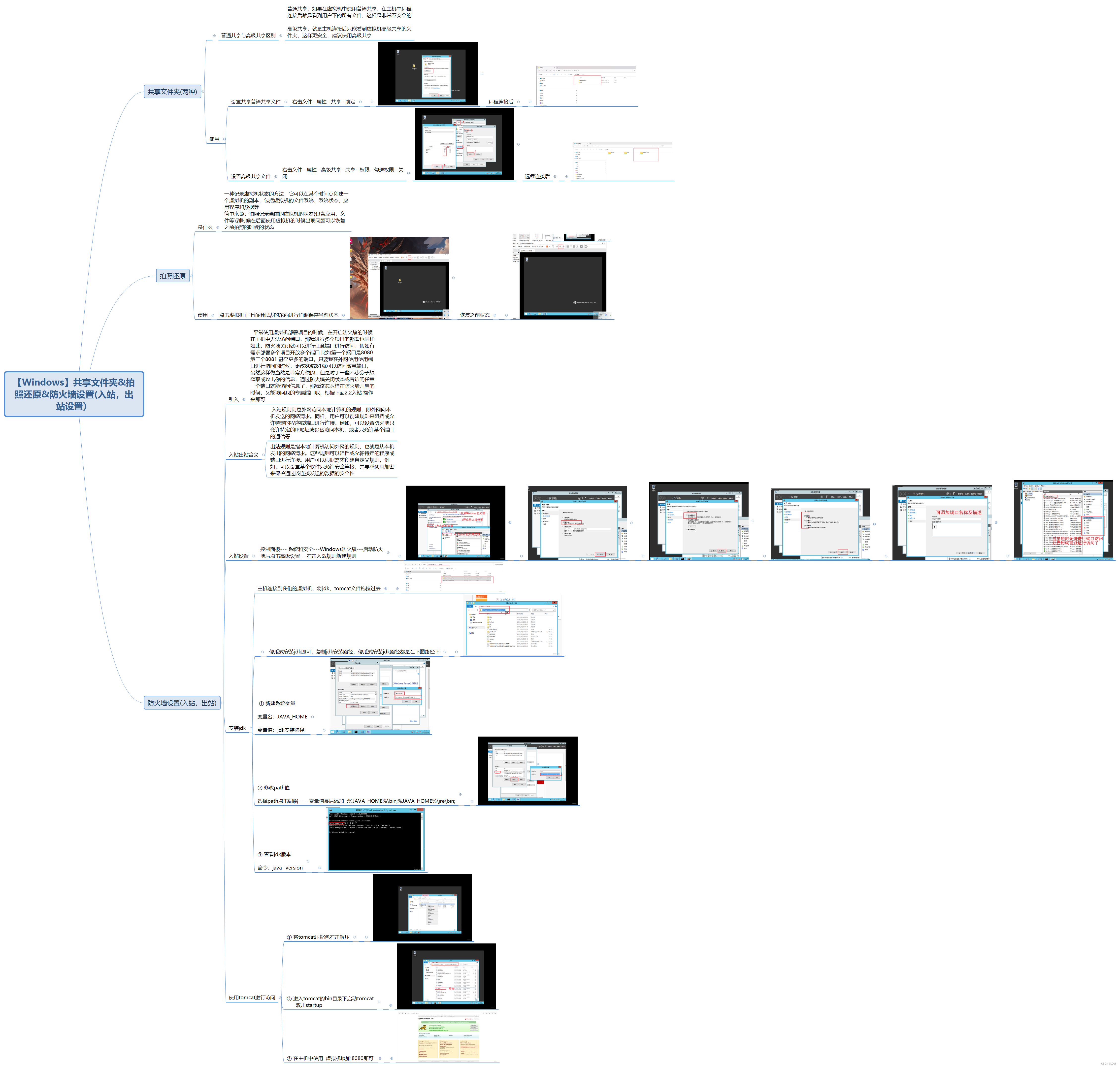
【Windows】共享文件夹拍照还原防火墙设置(入站，出站设置）---图文并茂详细讲解

目录 一 共享文件夹(两种形式) 1.1 普通共享与高级共享区别 1.2 使用 二 拍照还原 2.1 是什么 2.2 使用 三 防火墙设置（入栈，出站设置） 3.1 引入 3.2 入站出站设置 3.2.1入站出站含义 3.3入站设置 3.4安装jdk 3.5使用tomcat进行访…...

编程日记 2023/12/31 14:58:42

1.决策树

目录 1. 什么是决策树? 2. 决策树的原理 2.1 如何构建决策树？ 2.2 构建决策树的数据算法 2.2.1 信息熵 2.2.2 ID3算法 2.2.2.1 信息的定义 2.2.2.2 信息增益 2.2.2.3 ID3算法举例 2.2.2.4 ID3算法优缺点 2.2.3 C4.5算法 2.2.3.1 C4.5算法举例 2.2.4 CART算法 2.2.4…...

编程日记 2023/12/31 14:56:41

基于微信小程序的停车预约系统设计与实现

基于微信小程序的停车预约系统设计与实现 项目概述 本项目旨在结合微信小程序、后台Spring Boot和MySQL数据库，打造一套高效便捷的停车预约系统。用户通过微信小程序进行注册、登录、预约停车位等操作，而管理员和超级管理员则可通过后台管理系统对停车…...

编程日记 2023/12/31 14:55:40

再见2023，你好2024

再见2023，你好2024 生活1月 悲伤与治愈2~4月 运动与偏爱5月 体验与美食6月 婚礼与热爱7~8月 就医与别离9~11月 陪伴与暖房12月 体验&新生 运动追剧读书总结 生活 生活是一个修罗场，来世间一场，要经历丰腴有趣的人生。去体验各种滋味&…...

编程日记 2023/12/31 14:54:39

年度总结｜存储随笔2023年度最受欢迎文章榜单TOP15-part1

原创 古猫先生 存储随笔 2023-12-31 08:31 发表于上海 回首2023 2-8月份有近半年时间基本处于断更状态 好在8月份后小编没有松懈 （虽然2023年度总结，更像是近4个月总结） 本年度顺利加V啦！ 感谢各位粉丝朋友的一路支持与陪伴 …...

编程日记 2023/12/31 14:52:37

微信小程序 手机号授权登录 偶尔后端解密失败

微信小程序wx.login获取code要在手机号授权前触发 <button:id"code":open-type"hasGetPrivacySetting ? getPhoneNumber|agreePrivacyAuthorization : getPhoneNumber"getphonenumber"onGetPhoneNumber"class"btn"click"cli…...

编程日记 2023/12/31 14:49:34

Mysql 容易忘的 sql 指令总结

目录 一、操作数据库的基本指令 二、查询语句的指令 1、基本查询语句 2、模糊查询 3、分支查询 4、 分组查询 5、分组查询 6、基本查询总结&#xff1a; 7、子查询 8、连接查询 三、MySQL中的常用函数 1、时间函数 2、字符串函数 3、聚合函数 4、运算函数 四、表…...

编程日记 2023/12/31 14:47:33

【SD】tile 模型 - 固定衣服 生成人物 ☑

原理1&#xff1a;tile re 生成固定衣服的人物 tile1-1 re1-1 原理2&#xff1a;tile re 生成随机衣服的人物 tile0.5-1 re0.5-1 原理3&#xff1a;更改动作 必须使用衣服LORA 才可以进行穿衣服 测试大模型&#xff1a;###最爱的模型\meinamix_meinaV11.safe…...

编程日记 2023/12/31 14:42:28

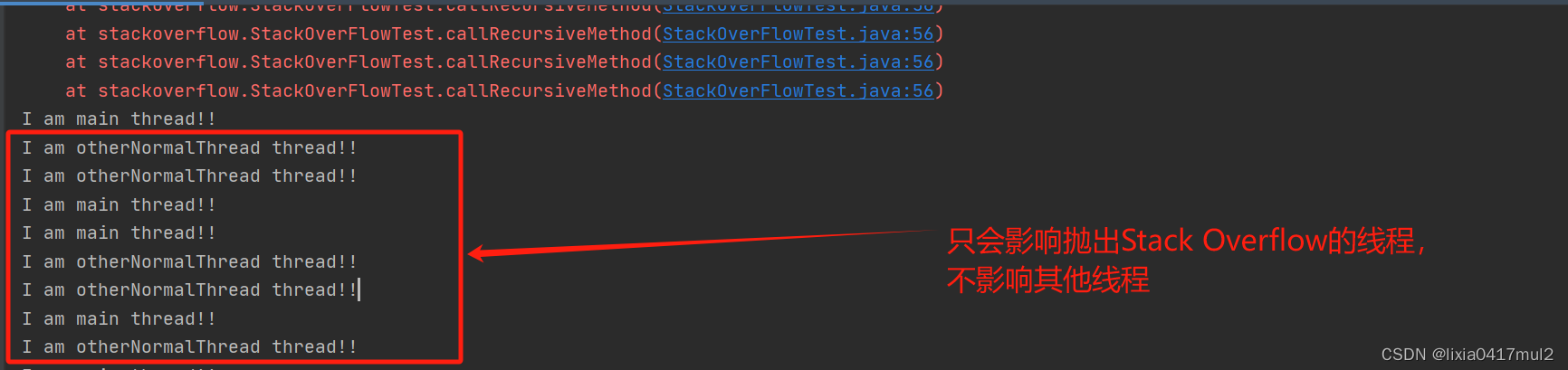
StackOverflowError的JVM处理方式

背景&#xff1a; 事情来源于生产的一个异常日志 Caused by: java.lang.StackOverflowError: null at java.util.stream.Collectors.lambda$groupingBy$45(Collectors.java:908) at java.util.stream.ReduceOps$3ReducingSink.accept(ReduceOps.java:169) at java.util.ArrayL…...

编程日记 2023/12/31 14:40:25

基于DFA算法实现敏感词过滤

何为DFA DFA&#xff0c;全称为Deterministic Finite Automaton&#xff0c;即确定有穷自动机、确定有限状态自动机或确定有限自动机 对于一个给定的属于该自动机的状态和一个属于该自动机字母表Σ的字符&#xff0c;它都能根据事先给定的转移函数转移到下一个状态&#xff0…...

编程日记 2023/12/31 14:36:21

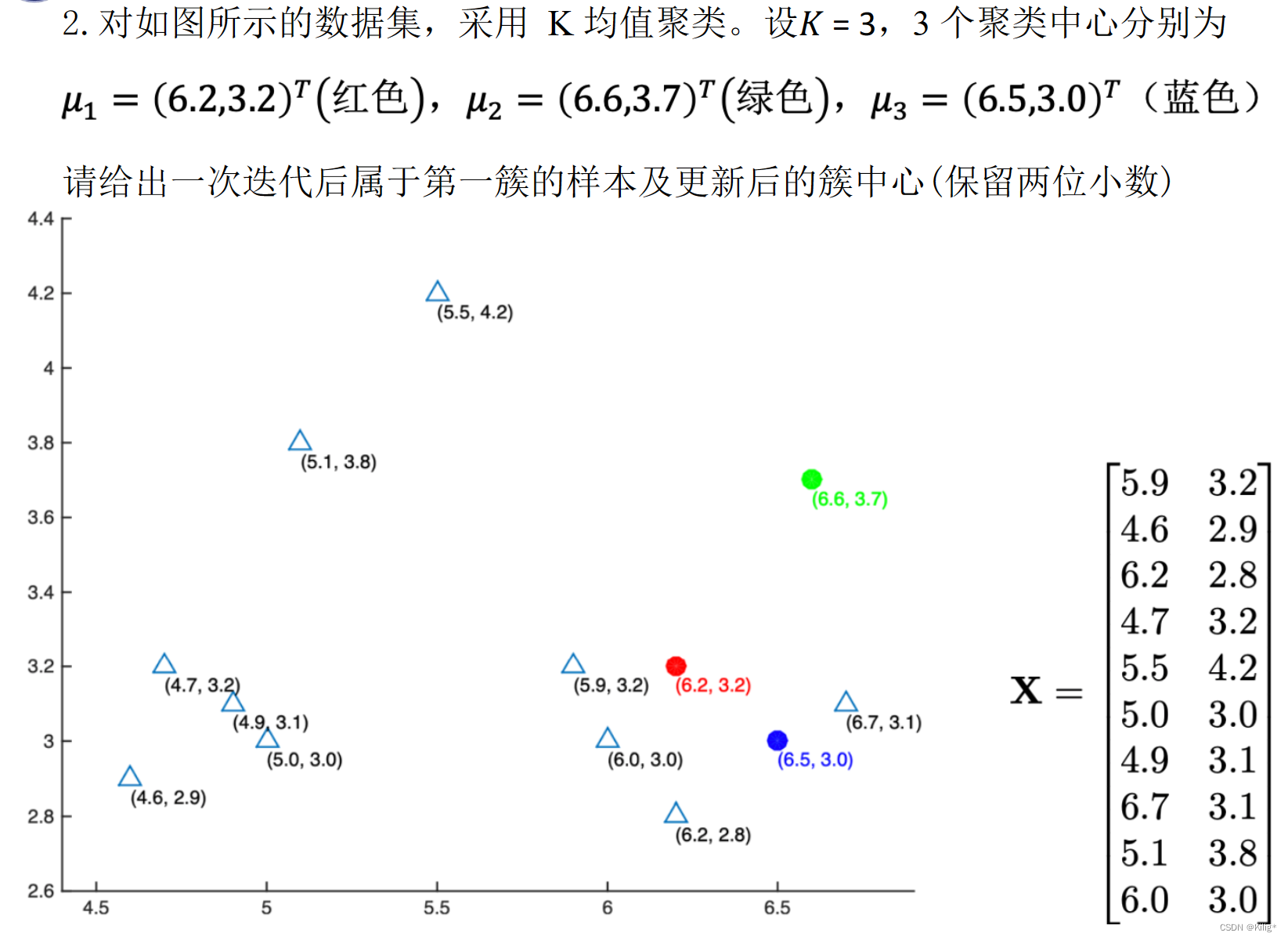
模式识别与机器学习-无监督学习-聚类

无监督学习-聚类 监督学习&无监督学习K-meansK-means聚类的优点&#xff1a;K-means的局限性&#xff1a;解决方案&#xff1a; 高斯混合模型&#xff08;Gaussian Mixture Models&#xff0c;GMM&#xff09;多维高斯分布的概率密度函数&#xff1a;高斯混合模型&#xff…...

编程日记 2023/12/31 14:35:20

Python中property特性属性是什么

在Java中&#xff0c;通常在类中定义的成员变量为私有变量&#xff0c;在类的实例中不能直接通过对象.属性直接操作&#xff0c;而是要通过getter和setter来操作私有变量。 而在Python中&#xff0c;因为有property这个概念&#xff0c;所以不需要写getter和setter一堆重复的代…...

编程日记 2023/12/31 14:32:17

vue3 全局配置Axios实例

目录 前言 配置Axios实例 页面使用 总结 前言 Axios 是一个基于 Promise 的 HTTP 客户端&#xff0c;用于浏览器和 Node.js 环境。它提供了一种简单、一致的 API 来处理HTTP请求&#xff0c;支持请求和响应的拦截、转换、取消请求等功能。关于它的作用&#xff1a; 发起 HTTP …...

编程日记 2023/12/31 14:31:16

EI级 | Matlab实现TCN-BiGRU-Multihead-Attention多头注意力机制多变量时间序列预测

EI级 | Matlab实现TCN-BiGRU-Multihead-Attention多头注意力机制多变量时间序列预测 目录 EI级 | Matlab实现TCN-BiGRU-Multihead-Attention多头注意力机制多变量时间序列预测预测效果基本介绍模型描述程序设计参考资料 预测效果 基本介绍 1.【EI级】 Matlab实现TCN-BiGRU-Mult…...

编程日记 2023/12/31 14:28:14

WeNet语音识别分词制作词云图

在线体验 ,点击识别语音需要等待一会&#xff0c;文件太大缓存会报错 介绍 本篇博客将介绍如何使用 Streamlit、jieba、wenet 和其他 Python 库&#xff0c;结合语音识别&#xff08;WeNet&#xff09;和词云生成&#xff0c;构建一个功能丰富的应用程序。我们将深入了解代码…...

编程日记 2023/12/31 14:26:12

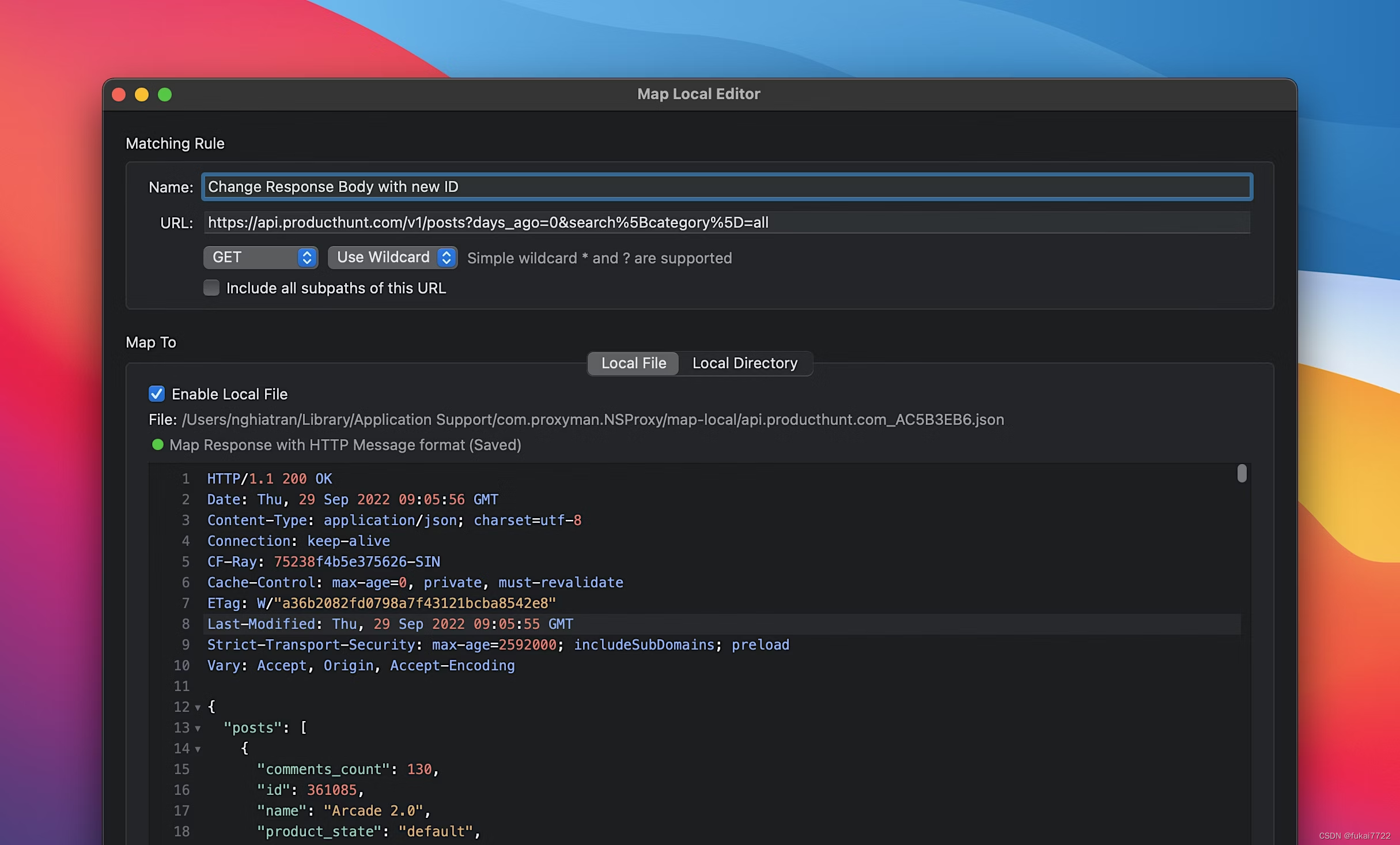
Proxyman：现代本地Web调试代理工具

1. 简介 1.1 什么是Proxyman&#xff1f; Proxyman是一款专为macOS设计的现代本地Web调试代理工具&#xff0c;它不仅支持macOS平台&#xff0c;还能无缝地与iOS和Android设备进行集成。作为一个网络调试工具&#xff0c;Proxyman的设计旨在提供高性能、直观且功能丰富的解决…...

编程日记 2023/12/31 14:23:09

k8s中DaemonSet实战详解

一、DaemonSet介绍 DaemonSet 的主要作用&#xff0c;是在 Kubernetes 集群里&#xff0c;运行一个 Daemon Pod。DaemonSet 只管理 Pod 对象&#xff0c;然后通过 nodeAffinity 和 Toleration 这两个调度器参数的功能&#xff0c;保证了每个节点上有且只有一个 Pod。 二、Daem…...

编程日记 2023/12/31 14:19:05

信号处理设计模式

问题 如何编写信号安全的应用程序&#xff1f; Linux 应用程序安全性讨论 场景一&#xff1a;不需要处理信号 应用程序实现单一功能&#xff0c;不需要关注信号 如&#xff1a;数据处理程序&#xff0c;文件加密程序&#xff0c;科学计算程序 场景二&#xff1a;需要处理信…...

编程日记 2023/12/31 14:17:03

五年级数学知识边界总结思考-下册

目录 一、背景二、过程1.观察物体小学五年级下册“观察物体”知识点详解&#xff1a;由来、作用与意义**一、知识点核心内容****二、知识点的由来&#xff1a;从生活实践到数学抽象****三、知识的作用&#xff1a;解决实际问题的工具****四、学习的意义&#xff1a;培养核心素养…...

编程新知 2025/10/7 4:57:55

Java面试专项一-准备篇

一、企业简历筛选规则 一般企业的简历筛选流程&#xff1a;首先由HR先筛选一部分简历后&#xff0c;在将简历给到对应的项目负责人后再进行下一步的操作。 HR如何筛选简历 例如&#xff1a;Boss直聘&#xff08;招聘方平台&#xff09; 直接按照条件进行筛选 例如&#xff1a…...

编程新知 2026/1/26 19:10:48

Android 之 kotlin 语言学习笔记三（Kotlin-Java 互操作）

参考官方文档&#xff1a;https://developer.android.google.cn/kotlin/interop?hlzh-cn 一、Java&#xff08;供 Kotlin 使用&#xff09; 1、不得使用硬关键字 不要使用 Kotlin 的任何硬关键字作为方法的名称 或字段。允许使用 Kotlin 的软关键字、修饰符关键字和特殊标识…...

编程新知 2026/2/8 0:33:04

Pinocchio 库详解及其在足式机器人上的应用

Pinocchio 库详解及其在足式机器人上的应用 Pinocchio (Pinocchio is not only a nose) 是一个开源的 C 库&#xff0c;专门用于快速计算机器人模型的正向运动学、逆向运动学、雅可比矩阵、动力学和动力学导数。它主要关注效率和准确性&#xff0c;并提供了一个通用的框架&…...

编程新知 2025/11/28 5:32:31

Linux C语言网络编程详细入门教程：如何一步步实现TCP服务端与客户端通信

文章目录 Linux C语言网络编程详细入门教程&#xff1a;如何一步步实现TCP服务端与客户端通信前言一、网络通信基础概念二、服务端与客户端的完整流程图解三、每一步的详细讲解和代码示例1. 创建Socket&#xff08;服务端和客户端都要&#xff09;2. 绑定本地地址和端口&#x…...

编程新知 2025/10/31 21:54:15

浪潮交换机配置track检测实现高速公路收费网络主备切换NQA

浪潮交换机track配置 项目背景高速网络拓扑网络情况分析通信线路收费网络路由 收费汇聚交换机相应配置收费汇聚track配置 项目背景 在实施省内一条高速公路时遇到的需求&#xff0c;本次涉及的主要是收费汇聚交换机的配置&#xff0c;浪潮网络设备在高速项目很少&#xff0c;通…...

编程新知 2026/2/6 13:10:51

springboot整合VUE之在线教育管理系统简介

可以学习到的技能 学会常用技术栈的使用 独立开发项目 学会前端的开发流程 学会后端的开发流程 学会数据库的设计 学会前后端接口调用方式 学会多模块之间的关联 学会数据的处理 适用人群 在校学生&#xff0c;小白用户&#xff0c;想学习知识的 有点基础&#xff0c;想要通过项…...

编程新知 2026/2/10 6:39:48

苹果AI眼镜：从“工具”到“社交姿态”的范式革命——重新定义AI交互入口的未来机会

在2025年的AI硬件浪潮中，苹果AI眼镜（Apple Glasses）正在引发一场关于“人机交互形态”的深度思考。它并非简单地替代AirPods或Apple Watch，而是开辟了一个全新的、日常可接受的AI入口。其核心价值不在于功能的堆叠，而在于如何通过形态设计打破社交壁垒，成为用户“全天佩戴…...

编程新知 2025/12/22 12:09:15

手机平板能效生态设计指令EU 2023/1670标准解读

手机平板能效生态设计指令EU 2023/1670标准解读 以下是针对欧盟《手机和平板电脑生态设计法规》(EU) 2023/1670 的核心解读&#xff0c;综合法规核心要求、最新修正及企业合规要点&#xff1a; 一、法规背景与目标 生效与强制时间 发布于2023年8月31日&#xff08;OJ公报&…...

编程新知 2026/2/2 11:58:16

【堆垛策略】设计方法

堆垛策略的设计是积木堆叠系统的核心&#xff0c;直接影响堆叠的稳定性、效率和容错能力。以下是分层次的堆垛策略设计方法&#xff0c;涵盖基础规则、优化算法和容错机制&#xff1a; 1. 基础堆垛规则 (1) 物理稳定性优先 重心原则&#xff1a; 大尺寸/重量积木在下&#xf…...

编程新知 2026/2/8 13:33:28