什么是SLAM中的回环检测,如果没有回环检测会怎样
目录
什么是回环检测
如果没有回环检测
SLAM(Simultaneous Localization and Mapping,即同时定位与地图构建)是一种使机器人或自动驾驶汽车能够在未知环境中建立地图的同时定位自身位置的技术。回环检测(Loop Closure Detection)是SLAM中的一个关键概念。
什么是回环检测
-
定义:回环检测是指在SLAM过程中识别机器人返回到之前访问过的位置的过程。简单来说,当机器人在探索过程中回到一个它之前已经访问过的地点时,回环检测会告诉系统,“你现在回到了一个已知位置”。
-
目的:回环检测的主要目的是纠正累积的导航误差。随着机器人的移动,其对自身位置的估计往往会逐渐偏离实际位置。通过识别已知的地点,系统可以调整地图和机器人位置的估计,提高整个系统的准确性。
-
实现方法:这通常通过比较当前的传感器读数(如摄像头图像或激光雷达扫描)与存储的地图数据来实现。如果发现匹配,就认为发生了回环。
如果没有回环检测
如果在SLAM(Simultaneous Localization and Mapping)系统中没有检测到回环,会出现几个问题,尤其是在长时间运行或机器人在较大区域内移动时,以下问题可能会发生:
-
累积误差:随着时间的推移,定位误差可能会累积,导致越来越大的定位偏差。这是因为每一步的小误差都可能在没有校正的情况下逐渐累加起来。
-
地图质量下降:由于定位误差的累积,构建的地图可能会出现扭曲或不一致,这会影响机器人的导航和任务执行能力。
-
导航效率降低:在没有准确地图的情况下,机器人的路径规划和导航效率可能会降低,可能无法找到最优或安全的路径。
-
环境变化的适应性差:在动态变化的环境中,缺乏回环检测可能导致机器人无法识别之前访问过的区域,从而无法有效适应环境变化。
-
无法识别已访问区域:回环检测的一个重要功能是让系统识别出机器人已经访问过的区域。如果没有回环检测,机器人可能无法意识到它已经返回到了一个已知位置,从而错过优化地图和定位的机会。
-
性能问题:在长时间的运行中,没有回环检测的累积误差可能导致性能问题,如机器人可能需要更频繁地重新定位或调整其路径。
总之,没有回环检测的SLAM系统可能会遇到准确度和性能问题,尤其是在长期运行或覆盖广阔区域时。回环检测是提高SLAM系统准确性和可靠性的关键组件。因此,回环检测在SLAM系统中非常重要,它有助于提高地图的准确性和机器人定位的可靠性,特别是在长时间运行或覆盖大区域时。
相关文章:

什么是SLAM中的回环检测,如果没有回环检测会怎样
目录 什么是回环检测 如果没有回环检测 SLAM(Simultaneous Localization and Mapping,即同时定位与地图构建)是一种使机器人或自动驾驶汽车能够在未知环境中建立地图的同时定位自身位置的技术。回环检测(Loop Closure Detectio…...

ubuntu 通过文件设置静态IP、DNS、网关
1. 确定网络接口名称 首先,使用 ip a 命令确定您要配置的网络接口名称。 2. 编辑 Netplan 配置文件 使用文本编辑器(如 nano)打开或创建 Netplan 配置文件: sudo nano /etc/netplan/01-netcfg.yaml3. 输入 Netplan 配置 在编…...
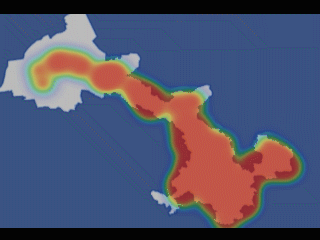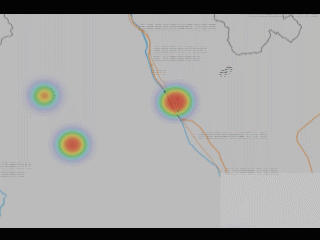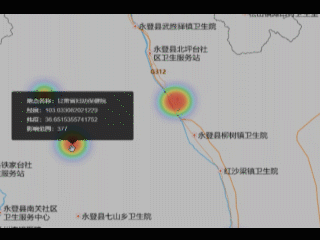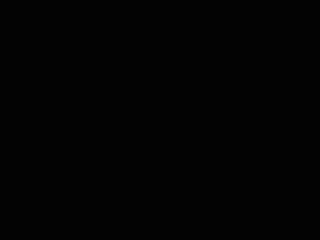
mapboxgl 中热力图的实现以及给热力图点增加鼠标移上 popup 效果
文章目录 概要效果预览技术思路技术细节小结 概要 本篇文章还是关于最近做到的 mapboxgl 地图展开的。 借鉴官方示例:https://iclient.supermap.io/examples/mapboxgl/editor.html#heatMapLayer 效果预览 技术思路 将接口数据渲染到地图中形成热力图。还需要将热…...
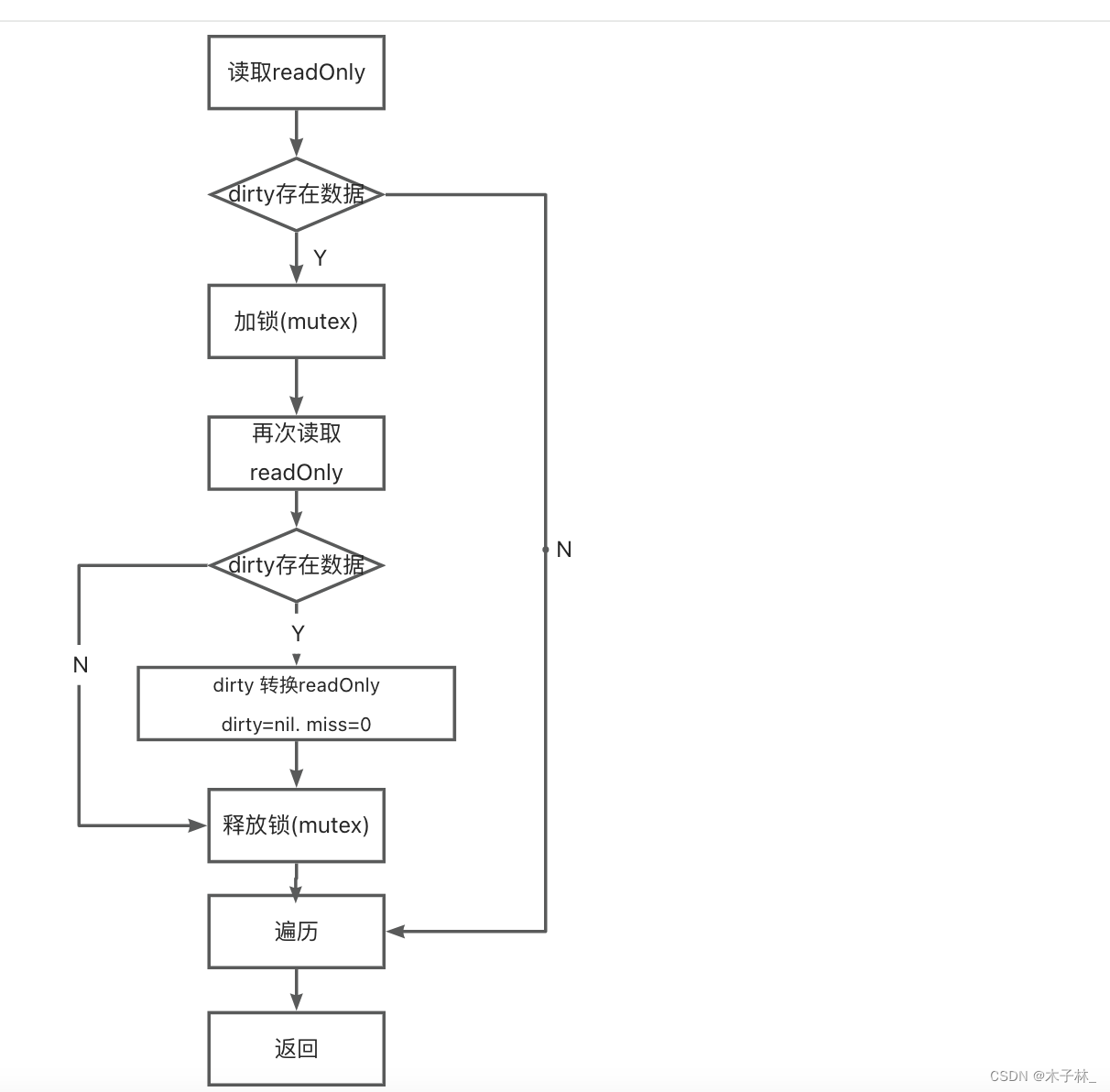
golang并发安全-sync.map
sync.map解决的问题 golang 原生map是存在并发读写的问题,在并发读写时候会抛出异常 func main() {mT : make(map[int]int)g1 : []int{1, 2, 3, 4, 5, 6}g2 : []int{4, 5, 6, 7, 8, 9}go func() {for i : range g1 {mT[i] i}}()go func() {for i : range g2 {mT[…...

开发第一个SpringBoot程序
使用命令创建Maven工程 mvn archetype:generate -DgroupIdorg.sang -DartifactIdchapter01 -DarchetypeArtifactIdmaven-archetype-quickstart -DinteractiveModefalse 参数说明: -DgroupId 组织Id(项目包名) -DartifactId 项目名称或模块…...

2023年度总结—你是你的年度MVP吗?
这段年度总结其实我之前就想写了,大概就是市赛比完之后18号的样子把,但是因为太懒了就一直拖到了现在哈哈,我思来想去,翻来覆去,彻夜难眠,想了想,还是决定把它写了吧!毕竟࿰…...

Linux基础知识学习3
vim编辑器 其分为四种模式 1.普通(命令)模式 2.编辑模式 3.底栏模式 4.可视化模式 vim编辑器被称为编辑器之神,而Emacs更是神之编辑器 普通模式: 1.光标移动 ^ 移动到行首 w 跳到下一个单词的开头…...
)
Leetcode5-在长度2N的数组中找出重复N次的元素(961)
1、题目 给你一个整数数组 nums ,该数组具有以下属性: nums.length 2 * n. nums 包含 n 1 个 不同的 元素 nums 中恰有一个元素重复 n 次 找出并返回重复了 n 次的那个元素。 示例 1: 输入:nums [1,2,3,3] 输出:…...

openssl的 openssl.cnf配置文件详解
背景:在上一篇文中,提到要写一篇openssl 配置文件详解的,这就来了~~~ find / -name openssl.cnf /etc/pki/tls/openssl.cnf /etc/pki/tls/openssl.cnf,该文件主要设置了证书请求、签名、crl相关的配置。主要相关的伪命令为ca和req…...
SpringBoot集成支付宝,看这一篇就够了。
前 言 在开始集成支付宝支付之前,我们需要准备一个支付宝商家账户,如果是个人开发者,可以通过注册公司或者让有公司资质的单位进行授权,后续在集成相关API的时候需要提供这些信息。 下面我以电脑网页端在线支付为例,介…...
数据结构程序设计——哈希表的应用(2)->哈希表解决冲突的方法
目录 实验须知 代码实现 实验报告 一:问题分析 二、数据结构 1.逻辑结构 2.物理结构 三、算法 (一)主要算法描述 1.用除留余数法构造哈希函数 2.线性探测再散列法 (一)主要算法实现代码 四、上机调试 实…...
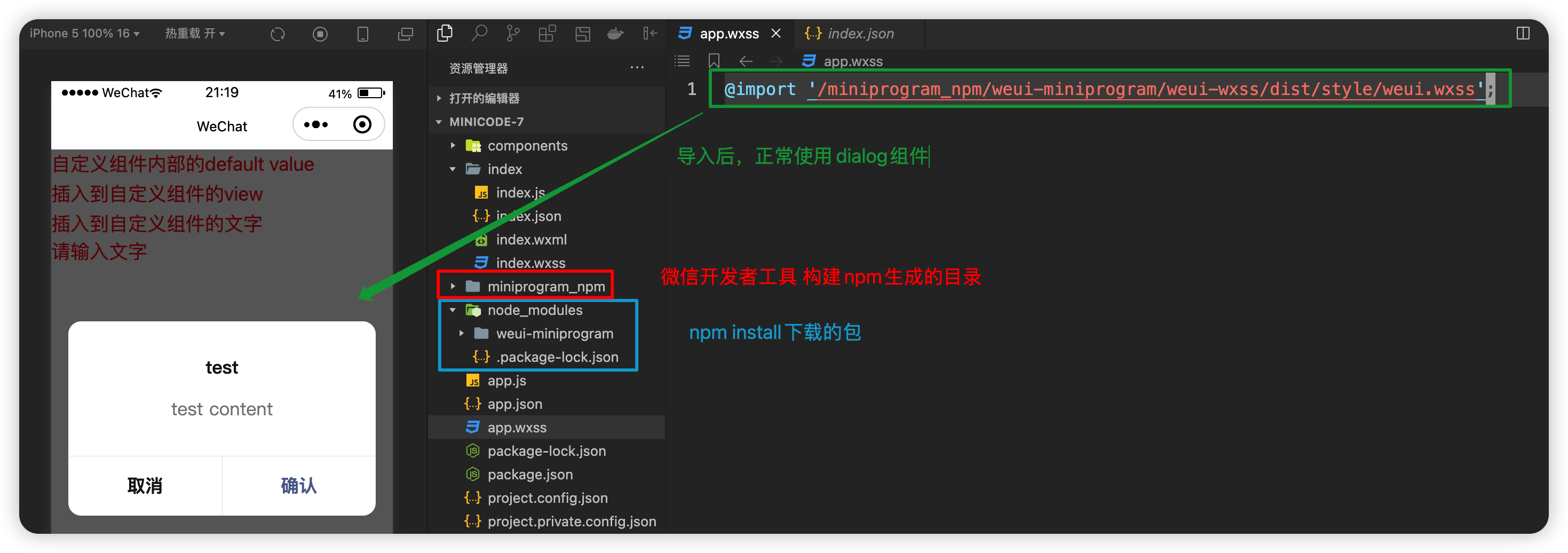
微信小程序开发系列-07组件
微信小程序开发系列目录 《微信小程序开发系列-01创建一个最小的小程序项目》《微信小程序开发系列-02注册小程序》《微信小程序开发系列-03全局配置中的“window”和“tabBar”》《微信小程序开发系列-04获取用户图像和昵称》《微信小程序开发系列-05登录小程序》《微信小程序…...

JavaScript 中 Set 和 Map 的区别
JavaScript 中的 Set 和 Map 都是用来存储数据的数据结构,它们之间的区别如下: Set 是一组唯一值的集合,而 Map 是一组键值对的集合。Set 中的值是唯一的,不允许重复;Map 中的键是唯一的,值可以重复。Set …...

web前端之JavaScript
MENU JavaScript之设计模式、单例、代理、装饰者、中介者、观察者、发布订阅、策略JavaScript之数组静态方法的实现、reduce、forEach、map、push、every JavaScript之设计模式、单例、代理、装饰者、中介者、观察者、发布订阅、策略 单例模式 概念 保证一个类仅有一个实例&am…...
C# 图标标注小工具-查看重复文件
目录 效果 项目 代码 下载 效果 项目 代码 using System; using System.Collections.Generic; using System.Data; using System.IO; using System.Linq; using System.Security.Cryptography; using System.Windows.Forms;namespace ImageDuplicate {public partial clas…...

浅谈冯诺依曼体系和操作系统
🌎冯诺依曼体系结构 文章目录 冯诺依曼体系结构 认识冯诺依曼体系结构 硬件分类 各个硬件的简单认识 输入输出设备 中央处理器 存储器 关于内存 对冯诺依曼体系的理解 操作系统 操作系统…...

Good Bye 2023
Good Bye 2023 Good Bye 2023 A. 2023 题意:序列a中所有数的乘积应为2023,现在给出序列中的n个数,找到剩下的k个数并输出,报告不可能。 思路:把所有已知的数字乘起来,判断是否整除2023,不够…...

多开工具对手机应用响应速度的优化与改进
多开工具对手机应用响应速度的优化与改进 摘要: 如今,手机应用的多样化和个性化需求不断增长,用户对应用的响应速度要求也越来越高。为了满足用户的需求,开发者们使用了多种技术手段进行应用的优化和改进。其中,多开工…...
文件批量整理,文件归类整理,文件批量归类
我们每天都要面对无数的文件,从工作报告、个人照片到电影和音乐。如何有效地管理和归类这些文件,成为了我们日常生活和工作中所要处理的。今天,小编就给大家介绍一款简单易用的工具——文件批量改名高手,助你轻松实现文件批量归类…...
Python+Django+Mysql+SimpleUI搭建后端用户管理系统(非常详细,每一步都清晰,列举了里面所有使用的方法属性)
一、在Anaconda环境下创建虚拟环境 (1)打开Anaconda Prompt(install),创建虚拟环境,如下图所示: 方法一:默认情况下虚拟环境创建在Anaconda安装目录下的envs文件夹中 conda create --name usermanage …...

【OSG学习笔记】Day 18: 碰撞检测与物理交互
物理引擎(Physics Engine) 物理引擎 是一种通过计算机模拟物理规律(如力学、碰撞、重力、流体动力学等)的软件工具或库。 它的核心目标是在虚拟环境中逼真地模拟物体的运动和交互,广泛应用于 游戏开发、动画制作、虚…...

【JavaEE】-- HTTP
1. HTTP是什么? HTTP(全称为"超文本传输协议")是一种应用非常广泛的应用层协议,HTTP是基于TCP协议的一种应用层协议。 应用层协议:是计算机网络协议栈中最高层的协议,它定义了运行在不同主机上…...

最新SpringBoot+SpringCloud+Nacos微服务框架分享
文章目录 前言一、服务规划二、架构核心1.cloud的pom2.gateway的异常handler3.gateway的filter4、admin的pom5、admin的登录核心 三、code-helper分享总结 前言 最近有个活蛮赶的,根据Excel列的需求预估的工时直接打骨折,不要问我为什么,主要…...

剑指offer20_链表中环的入口节点
链表中环的入口节点 给定一个链表,若其中包含环,则输出环的入口节点。 若其中不包含环,则输出null。 数据范围 节点 val 值取值范围 [ 1 , 1000 ] [1,1000] [1,1000]。 节点 val 值各不相同。 链表长度 [ 0 , 500 ] [0,500] [0,500]。 …...

【2025年】解决Burpsuite抓不到https包的问题
环境:windows11 burpsuite:2025.5 在抓取https网站时,burpsuite抓取不到https数据包,只显示: 解决该问题只需如下三个步骤: 1、浏览器中访问 http://burp 2、下载 CA certificate 证书 3、在设置--隐私与安全--…...

Python爬虫(一):爬虫伪装
一、网站防爬机制概述 在当今互联网环境中,具有一定规模或盈利性质的网站几乎都实施了各种防爬措施。这些措施主要分为两大类: 身份验证机制:直接将未经授权的爬虫阻挡在外反爬技术体系:通过各种技术手段增加爬虫获取数据的难度…...
详解:相对定位 绝对定位 固定定位)
css的定位(position)详解:相对定位 绝对定位 固定定位
在 CSS 中,元素的定位通过 position 属性控制,共有 5 种定位模式:static(静态定位)、relative(相对定位)、absolute(绝对定位)、fixed(固定定位)和…...

AI编程--插件对比分析:CodeRider、GitHub Copilot及其他
AI编程插件对比分析:CodeRider、GitHub Copilot及其他 随着人工智能技术的快速发展,AI编程插件已成为提升开发者生产力的重要工具。CodeRider和GitHub Copilot作为市场上的领先者,分别以其独特的特性和生态系统吸引了大量开发者。本文将从功…...

Caliper 配置文件解析:config.yaml
Caliper 是一个区块链性能基准测试工具,用于评估不同区块链平台的性能。下面我将详细解释你提供的 fisco-bcos.json 文件结构,并说明它与 config.yaml 文件的关系。 fisco-bcos.json 文件解析 这个文件是针对 FISCO-BCOS 区块链网络的 Caliper 配置文件,主要包含以下几个部…...

让回归模型不再被异常值“带跑偏“,MSE和Cauchy损失函数在噪声数据环境下的实战对比
在机器学习的回归分析中,损失函数的选择对模型性能具有决定性影响。均方误差(MSE)作为经典的损失函数,在处理干净数据时表现优异,但在面对包含异常值的噪声数据时,其对大误差的二次惩罚机制往往导致模型参数…...
