关于正态分布
目录
- 1.正态分布是什么
- 2.正态分布有什么用途
- 3.如何确定数据服从正态分布
本文简单介绍正态分布的基本概念和用途。
1.正态分布是什么
正态分布,也称为高斯分布,是由德国数学家卡尔·弗里德里希·高斯在研究测量误差时提出的。他发现许多自然现象和统计数据,如人的身高、考试成绩等,其分布形状都呈现出一种特定的钟形曲线,这就是正态分布。
正态分布的数学表达式是:
f(x) = 1 / (σ√2π) * e^(-(x-μ)^2 / 2σ^2)
其中,μ是均值,σ是标准差,e是自然对数的底数(约等于2.71828),π是圆周率(约等于3.14159)。
这个公式描述了正态分布的概率密度函数,即对于给定的x值,其对应的概率密度是多少。这个函数的图形是一个关于均值对称的钟形曲线,曲线在均值处达到峰值,然后两边逐渐下降,接近水平轴。
正态分布的得出是基于大量的观察和实验数据,以及数学推导。它是统计学和自然科学中的一个重要工具,被广泛应用于数据分析、质量控制、风险管理等领域。
在统计学的许多方面有着重大的影响,特别是在参数估计和假设检验上。
正态分布的特点:
- 形状:正态分布的图形是关于平均值对称的钟形曲线。曲线在平均值处达到峰值,然后两边逐渐下降,接近水平轴。
- 均值、中位数和众数:在正态分布中,均值、中位数和众数是相等的,都等于分布的峰值。
- 标准差:标准差决定了分布的宽度。标准差越大,分布越宽;标准差越小,分布越窄。
- 曲线下的面积:正态分布曲线下的面积(即概率)总和为1。
- 68-95-99.7规则:在正态分布中,约68%的数据值位于均值的一个标准差范围内,约95%的数据值位于均值的两个标准差范围内,约99.7%的数据值位于均值的三个标准差范围内。
2.正态分布有什么用途
正态分布在统计学和自然科学中有广泛的应用,以下是一些主要的用途:
- 数据分析:正态分布是许多统计分析方法的基础,例如假设检验、置信区间、线性回归等。如果数据服从正态分布,那么我们可以使用这些方法进行分析。
- 质量控制:在工业生产中,正态分布常用于质量控制。例如,产品的尺寸、重量等通常会围绕一个目标值上下波动,这种波动通常可以用正态分布来描述。
- 风险管理:在金融和保险领域,正态分布常用于风险管理。例如,投资组合的收益率、保险索赔的金额等通常假设为正态分布,以便进行风险评估和决策。
- 自然科学:在自然科学中,许多现象的观测值都服从正态分布,例如人的身高、血压等。因此,正态分布常用于这些领域的研究。
- 中心极限定理:中心极限定理是统计学中的一个重要定理,它表明,如果我们从任何形状的分布中抽取足够大的样本,那么样本均值的分布将接近正态分布。这使得正态分布在大样本统计推断中有广泛的应用。
3.如何确定数据服从正态分布
确定数据是否服从正态分布,通常可以通过以下几种方法:
- 直方图:将数据绘制成直方图,观察其形状是否接近正态分布的钟形曲线。这是一种直观的方法,但可能受到数据量和分组方式的影响。
- QQ图:QQ图是一种图形化的方法,可以用来检验数据是否服从某种分布。如果数据点在QQ图上接近一条直线,那么可以认为数据服从正态分布。
- 偏度和峰度:偏度是衡量数据分布偏斜程度的统计量,峰度是衡量数据分布峰态的统计量。如果数据服从正态分布,那么其偏度应接近0,峰度应接近3。
- 统计检验:有一些统计检验可以用来检验数据是否服从正态分布,例如Shapiro-Wilk检验、Kolmogorov-Smirnov检验、Anderson-Darling检验等。这些检验会给出一个p值,如果p值大于某个显著性水平(例如0.05),那么我们不能拒绝数据服从正态分布的假设。
以上方法都有各自的优点和局限性,通常需要结合使用。并且,即使数据不完全服从正态分布,也可能可以通过一些变换(例如对数变换、平方根变换等)使其接近正态分布。
相关文章:

关于正态分布
目录 1.正态分布是什么2.正态分布有什么用途3.如何确定数据服从正态分布 本文简单介绍正态分布的基本概念和用途。 1.正态分布是什么 正态分布,也称为高斯分布,是由德国数学家卡尔弗里德里希高斯在研究测量误差时提出的。他发现许多自然现象和统计数据…...

每日一练(编程题-C/C++)
目录 CSDN每日一练1. 2023/2/27- 一维数组的最大子数组和(类型:数组 难度:中等)2. 2023/4/7 - 小艺照镜子(类型:字符串 难度:困难)3. 2023/4/14 - 最近的回文数(难度:中等)4. 2023/2/1-蛇形矩阵(难度:困难)…...

Unity UnityWebRequest 在Mac上使用报CommectionError
今天是想把前两天写的Demo拿到Mac上打个IPA的完事我发现 在运行时释放游戏资源的时候UnityWebRequest返回的结果不是Success 查看Log发现是 req.result 是CommectionError error是 Cannot connect to destination host 代码如下: UnityWebRequest req UnityWebRequ…...

WorkPlus为企业打造私有化部署IM解决方案
在移动数字化时代,企业面临着如何全面掌控业务和生态的挑战。企业微信、钉钉、飞书、Teams等应用虽然提供了部分解决方案,但无法满足企业的私有化部署需求。此时,WorkPlus作为安全专属的移动数字化平台,被誉为移动应用的“航空母舰…...
QT上位机开发(抽奖软件)
【 声明:版权所有,欢迎转载,请勿用于商业用途。 联系信箱:feixiaoxing 163.com】 用抽奖软件抽奖,是一种很常见的抽奖方式。特别是写这篇文章的时候,正好处于2023年12月31日,也是一年中最后一天…...

雨课堂作业整理
第一次作业 1.下列序列是图序列的是( ) A.1,2,2,3,4,4,5 B.1,1,2,2,4,6,6 C.0,0,2&am…...

C#/WPF 只允许一个实例程序运行并将已运行程序置顶
使用用互斥量(System.Threading.Mutex): 同步基元,它只向一个线程授予对共享资源的独占访问权。在程序启动时候,请求一个互斥体,如果能获取对指定互斥的访问权,就职运行一个实例。 实例代码: /// <…...
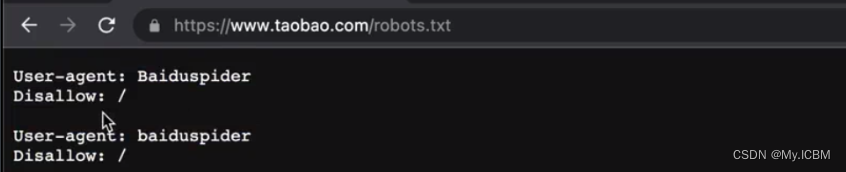
【基础】【Python网络爬虫】【1.认识爬虫】什么是爬虫,爬虫分类,爬虫可以做什么
Python网络爬虫基础 认识爬虫1.什么是爬虫2.爬虫可以做什么3.为什么用 Ptyhon 爬虫4.爬虫的分类通用爬虫聚焦爬虫功能爬虫增量式爬虫分布式爬虫 5.爬虫的矛与盾(重点)6.盗亦有道的君子协议robots7.爬虫合法性探究 认识爬虫 1.什么是爬虫 网络爬虫&…...
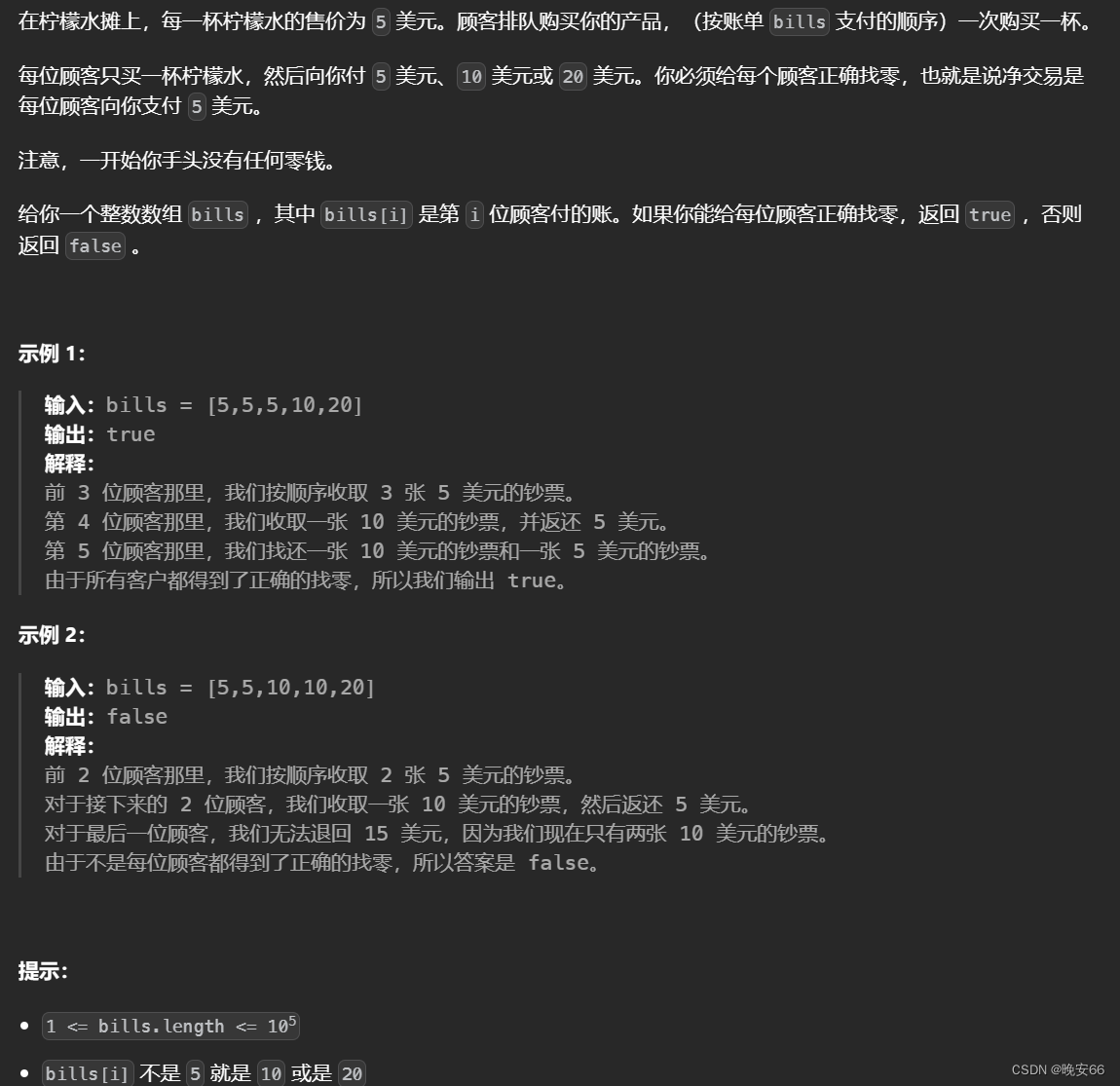
【算法与数据结构】860、LeetCode柠檬水找零
文章目录 一、题目二、解法三、完整代码 所有的LeetCode题解索引,可以看这篇文章——【算法和数据结构】LeetCode题解。 一、题目 二、解法 思路分析:本题的思路比较简单,首先要保存收到的零钱,其次计算找零,最后分解找…...

「Verilog学习笔记」乘法与位运算
专栏前言 本专栏的内容主要是记录本人学习Verilog过程中的一些知识点,刷题网站用的是牛客网 观察乘数的特点: 1111_1011 1_0000_0000 - 1 - 100 timescale 1ns/1nsmodule dajiang13(input [7:0] A,output [15:0] B);//*************code*********…...

CSS与JavaScript的简单认识
CSS:是一门语言,用于控制网页表现,让页面更好看的。 CSS(Cascading Style Sheet):层叠样式表 CSS与html结合的三种方式: 1、内部样式:用style标签,在标签内部定义CSS样式…...
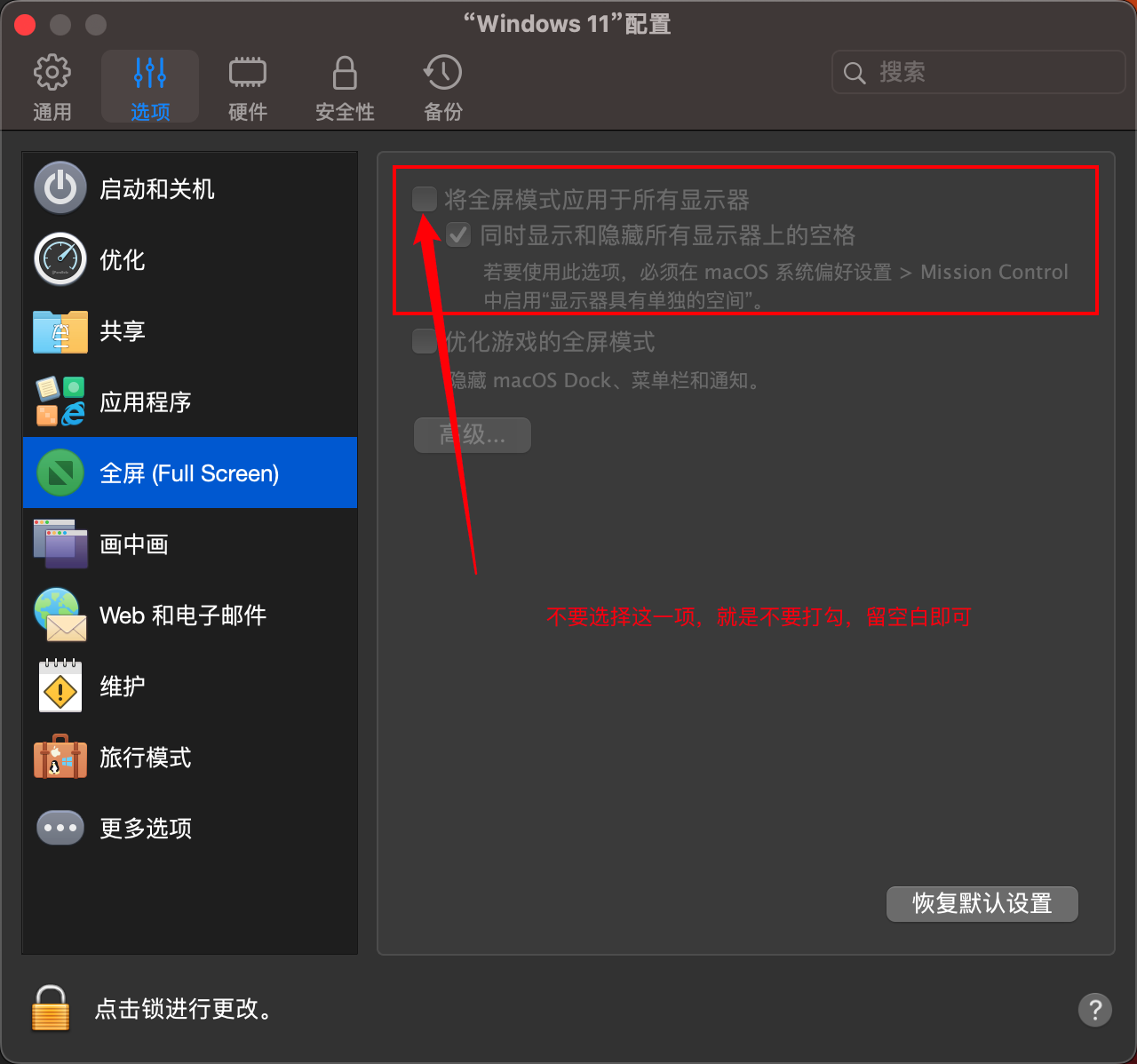
MAC 中多显示器的设置(Parallels Desktop)
目录 一、硬件列表: 二、线路连接: 三、软件设置: 1. 设置显示器排列位置及显示参数 2. 分别设置外接显示器为:扩展显示器,内建显示器为主显示器 3. 设置Parallels Desktop屏幕参数 四、结果 一、硬件列表&a…...

迁移到云原生:如何使用微服务迁移应用程序
企业遇到大规模部署和监督生产中的应用程序的任务。幸运的是,我们可以使用大量技术和工具。然而,从传统的,整体的结构转变为云态一个人提出了自己的障碍。在这里,您会发现将应用程序从整体设置转移到基于微服务的体系结构时要进行…...
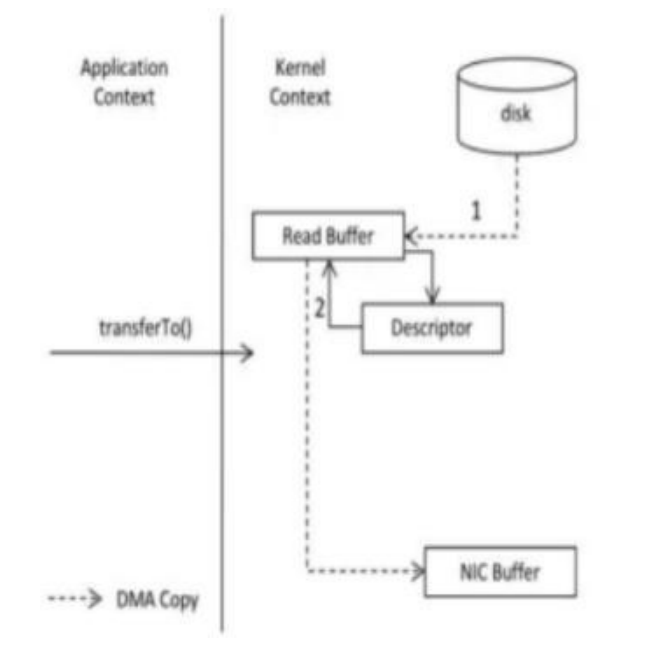
kafka 的零拷贝原理
文章目录 kafka 的零拷贝原理 今天来跟大家聊聊kafka的零拷贝原理是什么? kafka 的零拷贝原理 零拷贝是一种减少数据拷贝的机制,能够有效提升数据的效率; 在实际应用中,如果我们需要把磁盘中的某个文件内容发送到远程服务器上…...
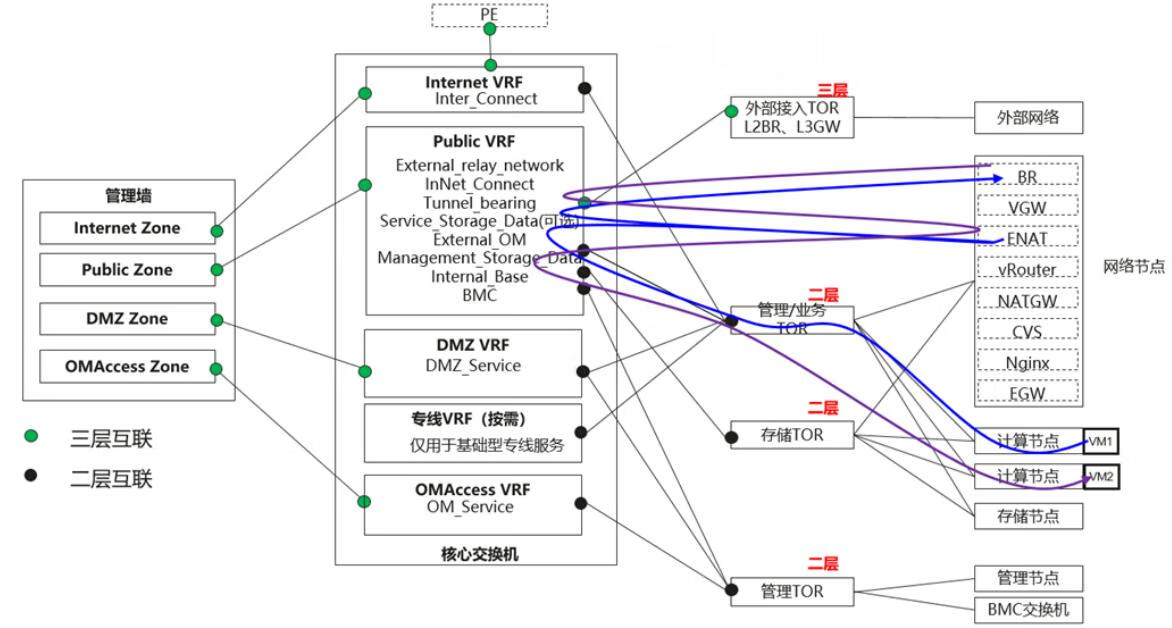
华为云Stack 8.X流量模型分析(五)
六、EIP流量模型分析 弹性公网IP(Elastic IP,简称EIP)提供独立的公网IP资源,包括公网IP地址与公网出口带宽服务。如果资源只配置了私网IP,则无法直接访问Internet,为资源配置弹性公网IP后,可…...

学习动态规划解决不同路径、最小路径和、打家劫舍、打家劫舍iii
学习动态规划|不同路径、最小路径和、打家劫舍、打家劫舍iii 62 不同路径 动态规划,dp[i][j]表示从左上角到(i,j)的路径数量dp[i][j] dp[i-1][j] dp[i][j-1] import java.util.Arrays;/*** 路径数量* 动态规划,dp[i][j]表示从左上角到(i,j)的路径数量…...

nodejs微信小程序+python+PHP特困救助供养信息管理系统-计算机毕业设计推荐
目 录 摘 要 I ABSTRACT II 目 录 II 第1章 绪论 1 1.1背景及意义 1 1.2 国内外研究概况 1 1.3 研究的内容 1 第2章 相关技术 3 2.1 nodejs简介 4 2.2 express框架介绍 6 2.4 MySQL数据库 4 第3章 系统分析 5 3.1 需求分析 5 3.2 系统可行性分析 5 3.2.1技术可行性:…...

Vue(二):计算属性与 watch 监听器
03. Vue 指令拓展 3.1 指令修饰符 可以通过 . 来指明一些指令的后缀,不同的后缀中封装了不同的操作,可以帮助我们简化代码,比如之前使用过的监听 enter 键的弹起,我们需要操作事件对象,来检测用户使用了哪个键&#…...

25、WEB攻防——通用漏洞SQL读写注入MYSQLMSSQLPostgreSQL
文章目录 Mysql-root高权限读写注入PostgreSQL——dba高权限读写注入Mssql-sa高权限读写注入 Access无高权限注入点——只能猜解,而且是暴力猜解; MYSQL,PostgreSQL,MSSQL(SQL server)高权限注入点——可升级读写(文件…...

【第5期】前端Vue使用Proxy+Vuex(store、mutations、actions)跨域调通本地后端接口
本期简介 本期要点 本地开发前后端如何跨域调用全局请求、响应处理拦截器处理封装HTTP请求模块编写API请求映射到后端API数据的状态管理 一、 本地开发前后端如何跨域调用 众所周知,只要前端和后端的域名或端口不一样,就存在跨域访问,例如&…...

【大模型RAG】拍照搜题技术架构速览:三层管道、两级检索、兜底大模型
摘要 拍照搜题系统采用“三层管道(多模态 OCR → 语义检索 → 答案渲染)、两级检索(倒排 BM25 向量 HNSW)并以大语言模型兜底”的整体框架: 多模态 OCR 层 将题目图片经过超分、去噪、倾斜校正后,分别用…...

Android Wi-Fi 连接失败日志分析
1. Android wifi 关键日志总结 (1) Wi-Fi 断开 (CTRL-EVENT-DISCONNECTED reason3) 日志相关部分: 06-05 10:48:40.987 943 943 I wpa_supplicant: wlan0: CTRL-EVENT-DISCONNECTED bssid44:9b:c1:57:a8:90 reason3 locally_generated1解析: CTR…...

深入剖析AI大模型:大模型时代的 Prompt 工程全解析
今天聊的内容,我认为是AI开发里面非常重要的内容。它在AI开发里无处不在,当你对 AI 助手说 "用李白的风格写一首关于人工智能的诗",或者让翻译模型 "将这段合同翻译成商务日语" 时,输入的这句话就是 Prompt。…...
)
进程地址空间(比特课总结)
一、进程地址空间 1. 环境变量 1 )⽤户级环境变量与系统级环境变量 全局属性:环境变量具有全局属性,会被⼦进程继承。例如当bash启动⼦进程时,环 境变量会⾃动传递给⼦进程。 本地变量限制:本地变量只在当前进程(ba…...

Golang 面试经典题:map 的 key 可以是什么类型?哪些不可以?
Golang 面试经典题:map 的 key 可以是什么类型?哪些不可以? 在 Golang 的面试中,map 类型的使用是一个常见的考点,其中对 key 类型的合法性 是一道常被提及的基础却很容易被忽视的问题。本文将带你深入理解 Golang 中…...

聊聊 Pulsar:Producer 源码解析
一、前言 Apache Pulsar 是一个企业级的开源分布式消息传递平台,以其高性能、可扩展性和存储计算分离架构在消息队列和流处理领域独树一帜。在 Pulsar 的核心架构中,Producer(生产者) 是连接客户端应用与消息队列的第一步。生产者…...

【C语言练习】080. 使用C语言实现简单的数据库操作
080. 使用C语言实现简单的数据库操作 080. 使用C语言实现简单的数据库操作使用原生APIODBC接口第三方库ORM框架文件模拟1. 安装SQLite2. 示例代码:使用SQLite创建数据库、表和插入数据3. 编译和运行4. 示例运行输出:5. 注意事项6. 总结080. 使用C语言实现简单的数据库操作 在…...

uniapp 开发ios, xcode 提交app store connect 和 testflight内测
uniapp 中配置 配置manifest 文档:manifest.json 应用配置 | uni-app官网 hbuilderx中本地打包 下载IOS最新SDK 开发环境 | uni小程序SDK hbulderx 版本号:4.66 对应的sdk版本 4.66 两者必须一致 本地打包的资源导入到SDK 导入资源 | uni小程序SDK …...

c++第七天 继承与派生2
这一篇文章主要内容是 派生类构造函数与析构函数 在派生类中重写基类成员 以及多继承 第一部分:派生类构造函数与析构函数 当创建一个派生类对象时,基类成员是如何初始化的? 1.当派生类对象创建的时候,基类成员的初始化顺序 …...

Proxmox Mail Gateway安装指南:从零开始配置高效邮件过滤系统
💝💝💝欢迎莅临我的博客,很高兴能够在这里和您见面!希望您在这里可以感受到一份轻松愉快的氛围,不仅可以获得有趣的内容和知识,也可以畅所欲言、分享您的想法和见解。 推荐:「storms…...
