QT上位机开发(抽奖软件)
【 声明:版权所有,欢迎转载,请勿用于商业用途。 联系信箱:feixiaoxing @163.com】
用抽奖软件抽奖,是一种很常见的抽奖方式。特别是写这篇文章的时候,正好处于2023年12月31日,也是一年中最后一天。虽然今年过年晚一点,但是2到3个星期之后,基本上各家公司都会准备年终尾牙的活动了。年会上吃饭、表演节目这是标配,不过重头戏还是抽奖,因为它会极大地调动员工的情绪,也会让员工更有归属感。
最近我们学习了QT程序,正好可以用QT设计一个简单的抽奖程序。
1、利用qt designer进行界面设计
界面设计比较简单,主要就是3个label和2个按钮。label的作用,就是显示最终的中奖号码。2个按钮,一个是启动,一个是结束。启动按钮按下去的时候,3个数字开始跳动;结束按钮按下去的时候,数字停止跳动。最终留下来的数字,提示我们幸运儿就是这位朋友。
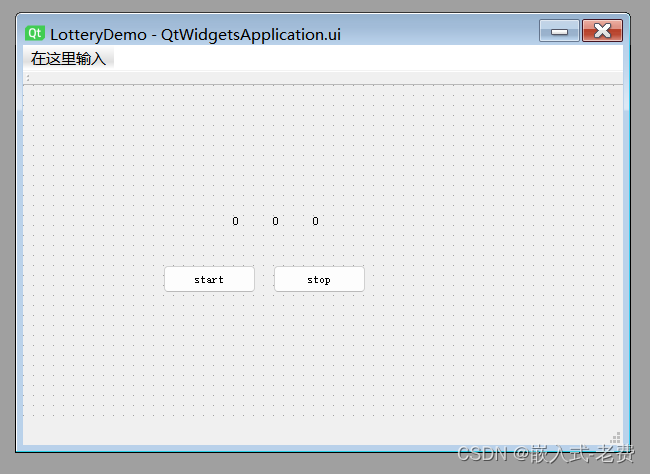
2、QtWidgetsApplication.h头文件
代码实现部分呢,有点类似于前面两篇文章的结合,同时增加一个随机数生成的功能。首先,两个按钮肯定需要绑定必要的按钮回调函数。其次,按钮按下去的时候,会触发定时器操作,这又相当于之前倒计时软件的设计。最后,因为每次需要显示的数据不同,所以还需要增加一个随机数生成的功能。要实现这些功能,我们看下头文件怎么设计,
#pragma once#include <QtWidgets/QMainWindow>
#include <QTimer>
#include "ui_QtWidgetsApplication.h"class QtWidgetsApplication : public QMainWindow
{Q_OBJECTpublic:QtWidgetsApplication(QWidget *parent = nullptr);~QtWidgetsApplication();private:Ui::QtWidgetsApplicationClass ui;QTimer* p_timer;int num;int flag;void display_number();private slots:void update();void on_start_clicked();void on_stop_clicked();
};
3、QtWidgetsApplication.cpp文件编写
要实现前面需要的功能,还是要一步一步来开发。通常,我们先处理下构造函数和析构函数;随后处理按钮回调函数;最后处理定时器函数的部分。
#include <QRandomGenerator>#include "QtWidgetsApplication.h"QtWidgetsApplication::QtWidgetsApplication(QWidget *parent): QMainWindow(parent)
{ui.setupUi(this);//set font and colorQFont ft;ft.setPointSize(20);ui.label1->setFont(ft);ui.label2->setFont(ft);ui.label3->setFont(ft);ui.label1->setStyleSheet("color: blue;");ui.label2->setStyleSheet("color: blue;");ui.label3->setStyleSheet("color: blue;");#if 0 // set title in ui file by feixiaoxing<property name = "windowTitle"><string>LotteryDemo< / string>< / property>
#endif// initialize variablenum = 0;flag = 0;p_timer = NULL;// connect button with functionconnect(ui.pushButton1, &QPushButton::clicked, this, &QtWidgetsApplication::on_start_clicked);connect(ui.pushButton2, &QPushButton::clicked, this, &QtWidgetsApplication::on_stop_clicked);ui.pushButton1->setEnabled(true);ui.pushButton2->setEnabled(false);// display number heredisplay_number();
}// destructor function
QtWidgetsApplication::~QtWidgetsApplication()
{if (p_timer) delete p_timer;
}// shou data here
void QtWidgetsApplication::display_number()
{ui.label1->setText(QString::number(num / 100));ui.label2->setText(QString::number((num % 100) / 10));ui.label3->setText(QString::number(num % 10));
}类的构造函数和析构函数非常重要,很多资源的申请和释放都是放在这里。当然,这里不仅包括了上面说的两个函数,还有一个display_number函数。大部分内容,都是之前文章已经讨论过的,这里不再赘述。唯一需要补充的,就是窗口标题的修改。目前为止,个人认为比较好的办法还是直接修改ui文件。
// start button callback function
void QtWidgetsApplication::on_start_clicked()
{// release previous timerif (p_timer){delete p_timer;p_timer = NULL;}// create a num, 0~999num = QRandomGenerator::global()->bounded(1000);// create timerp_timer = new QTimer(this);connect(p_timer, SIGNAL(timeout()), this, SLOT(update()));p_timer->start(20); // 20 is intervaldisplay_number();// set buttonui.pushButton1->setEnabled(false);ui.pushButton2->setEnabled(true);
}// timeout callback function
void QtWidgetsApplication::update()
{if (flag){p_timer->stop();delete p_timer;p_timer = NULL;flag = 0;return;}num = QRandomGenerator::global()->bounded(1000);display_number();
}处理完了构造函数、析构函数,剩下来就是按钮的处理。start按钮的回调已经在构造函数中注册好了,当然stop也是一样。我们只需要实现具体的内容即可。因为是抽奖,它和倒计时不一样,所以定时器的创建和回调需要在按钮触发的时候才能添加,这和之前不太一样。当然函数中涉及到了随机数,引用QRandomGenerator处理一下即可。
// stop button callback function
void QtWidgetsApplication::on_stop_clicked()
{flag = 1;ui.pushButton1->setEnabled(true);ui.pushButton2->setEnabled(false);
}
有开始就有结束。这里结束的处理方式就是flag置位,同时灰化一个按钮,高亮一个按钮。前面定时器回调的时候也用到了这个flag置位,即如果发现flag为1,立即停止定时器、删除定时器。
4、测试和验证
代码本身不复杂,直接拿过来编译和测试即可。编译无误的话,首先单击start,数字是否开始跳动;继续单击stop,数字是否不再跳动。如此操作几次,没有发现问题的话,就说明我们开发的代码是ok的,不然就要回去检查一下原因了,看看问题发生在什么地方。
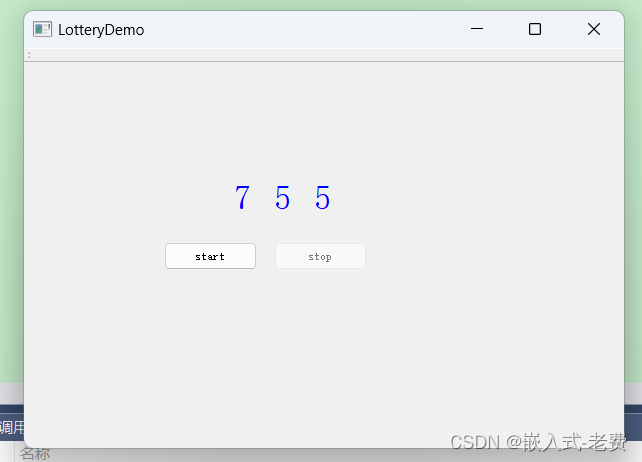
相关文章:

QT上位机开发(抽奖软件)
【 声明:版权所有,欢迎转载,请勿用于商业用途。 联系信箱:feixiaoxing 163.com】 用抽奖软件抽奖,是一种很常见的抽奖方式。特别是写这篇文章的时候,正好处于2023年12月31日,也是一年中最后一天…...

雨课堂作业整理
第一次作业 1.下列序列是图序列的是( ) A.1,2,2,3,4,4,5 B.1,1,2,2,4,6,6 C.0,0,2&am…...

C#/WPF 只允许一个实例程序运行并将已运行程序置顶
使用用互斥量(System.Threading.Mutex): 同步基元,它只向一个线程授予对共享资源的独占访问权。在程序启动时候,请求一个互斥体,如果能获取对指定互斥的访问权,就职运行一个实例。 实例代码: /// <…...
【基础】【Python网络爬虫】【1.认识爬虫】什么是爬虫,爬虫分类,爬虫可以做什么
Python网络爬虫基础 认识爬虫1.什么是爬虫2.爬虫可以做什么3.为什么用 Ptyhon 爬虫4.爬虫的分类通用爬虫聚焦爬虫功能爬虫增量式爬虫分布式爬虫 5.爬虫的矛与盾(重点)6.盗亦有道的君子协议robots7.爬虫合法性探究 认识爬虫 1.什么是爬虫 网络爬虫&…...
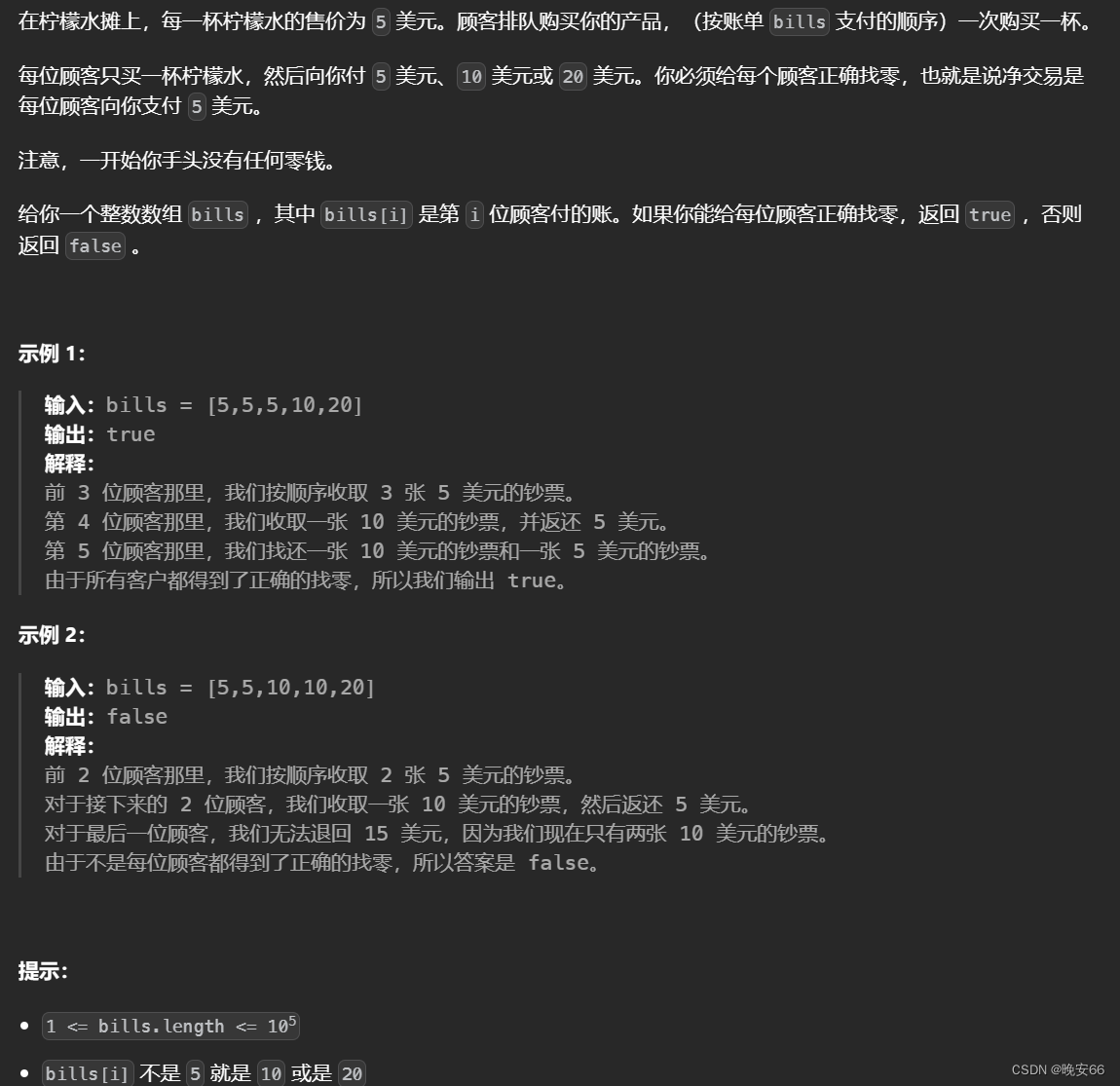
【算法与数据结构】860、LeetCode柠檬水找零
文章目录 一、题目二、解法三、完整代码 所有的LeetCode题解索引,可以看这篇文章——【算法和数据结构】LeetCode题解。 一、题目 二、解法 思路分析:本题的思路比较简单,首先要保存收到的零钱,其次计算找零,最后分解找…...

「Verilog学习笔记」乘法与位运算
专栏前言 本专栏的内容主要是记录本人学习Verilog过程中的一些知识点,刷题网站用的是牛客网 观察乘数的特点: 1111_1011 1_0000_0000 - 1 - 100 timescale 1ns/1nsmodule dajiang13(input [7:0] A,output [15:0] B);//*************code*********…...

CSS与JavaScript的简单认识
CSS:是一门语言,用于控制网页表现,让页面更好看的。 CSS(Cascading Style Sheet):层叠样式表 CSS与html结合的三种方式: 1、内部样式:用style标签,在标签内部定义CSS样式…...
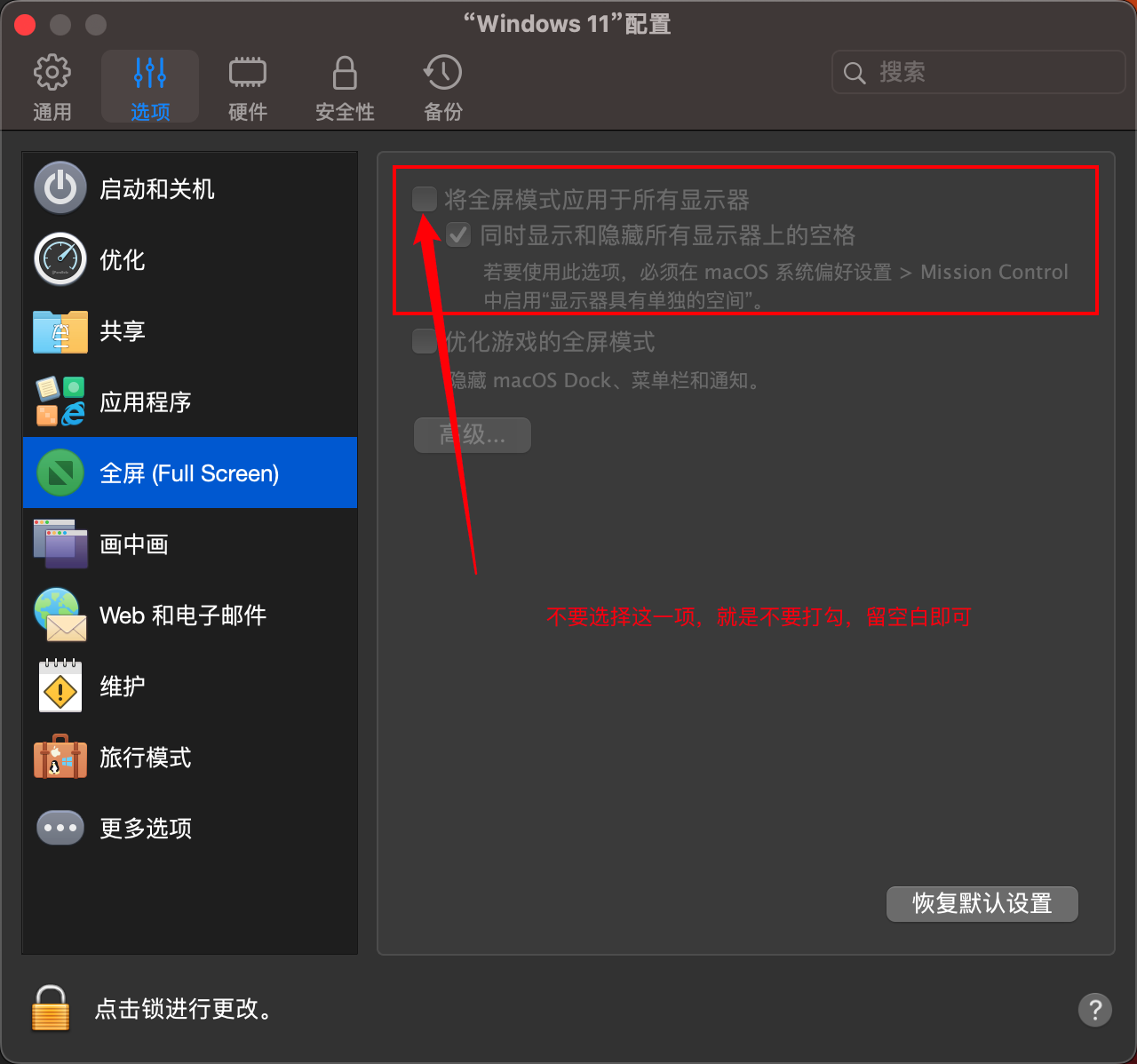
MAC 中多显示器的设置(Parallels Desktop)
目录 一、硬件列表: 二、线路连接: 三、软件设置: 1. 设置显示器排列位置及显示参数 2. 分别设置外接显示器为:扩展显示器,内建显示器为主显示器 3. 设置Parallels Desktop屏幕参数 四、结果 一、硬件列表&a…...

迁移到云原生:如何使用微服务迁移应用程序
企业遇到大规模部署和监督生产中的应用程序的任务。幸运的是,我们可以使用大量技术和工具。然而,从传统的,整体的结构转变为云态一个人提出了自己的障碍。在这里,您会发现将应用程序从整体设置转移到基于微服务的体系结构时要进行…...
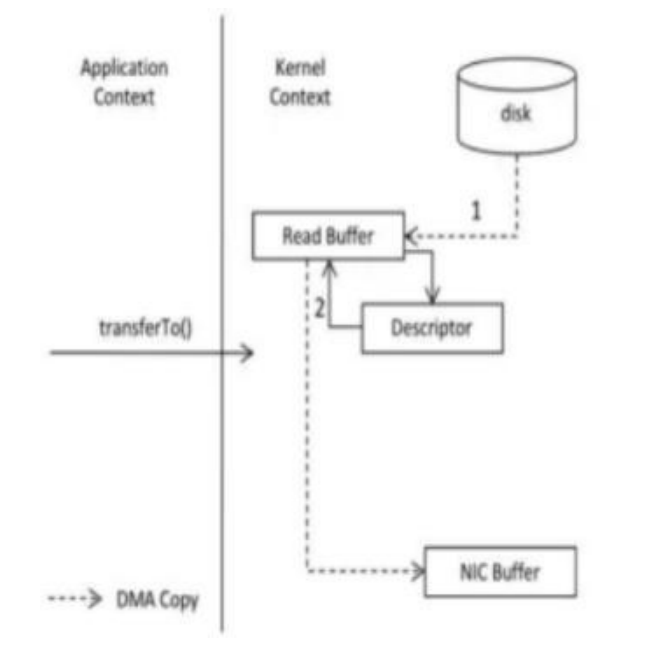
kafka 的零拷贝原理
文章目录 kafka 的零拷贝原理 今天来跟大家聊聊kafka的零拷贝原理是什么? kafka 的零拷贝原理 零拷贝是一种减少数据拷贝的机制,能够有效提升数据的效率; 在实际应用中,如果我们需要把磁盘中的某个文件内容发送到远程服务器上…...
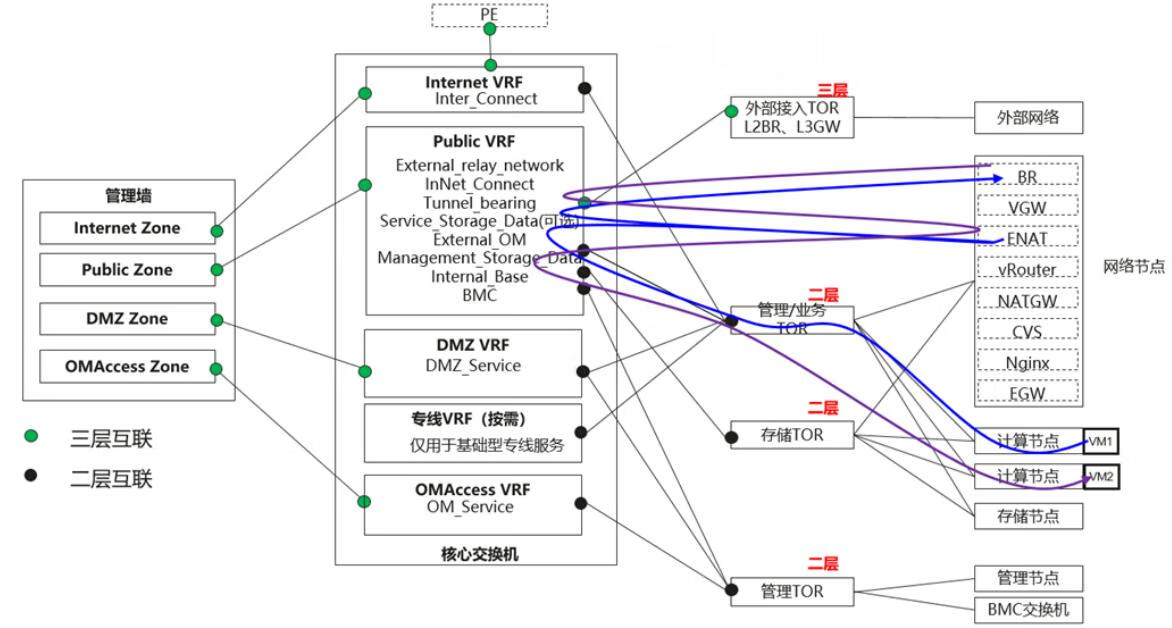
华为云Stack 8.X流量模型分析(五)
六、EIP流量模型分析 弹性公网IP(Elastic IP,简称EIP)提供独立的公网IP资源,包括公网IP地址与公网出口带宽服务。如果资源只配置了私网IP,则无法直接访问Internet,为资源配置弹性公网IP后,可…...

学习动态规划解决不同路径、最小路径和、打家劫舍、打家劫舍iii
学习动态规划|不同路径、最小路径和、打家劫舍、打家劫舍iii 62 不同路径 动态规划,dp[i][j]表示从左上角到(i,j)的路径数量dp[i][j] dp[i-1][j] dp[i][j-1] import java.util.Arrays;/*** 路径数量* 动态规划,dp[i][j]表示从左上角到(i,j)的路径数量…...

nodejs微信小程序+python+PHP特困救助供养信息管理系统-计算机毕业设计推荐
目 录 摘 要 I ABSTRACT II 目 录 II 第1章 绪论 1 1.1背景及意义 1 1.2 国内外研究概况 1 1.3 研究的内容 1 第2章 相关技术 3 2.1 nodejs简介 4 2.2 express框架介绍 6 2.4 MySQL数据库 4 第3章 系统分析 5 3.1 需求分析 5 3.2 系统可行性分析 5 3.2.1技术可行性:…...

Vue(二):计算属性与 watch 监听器
03. Vue 指令拓展 3.1 指令修饰符 可以通过 . 来指明一些指令的后缀,不同的后缀中封装了不同的操作,可以帮助我们简化代码,比如之前使用过的监听 enter 键的弹起,我们需要操作事件对象,来检测用户使用了哪个键&#…...

25、WEB攻防——通用漏洞SQL读写注入MYSQLMSSQLPostgreSQL
文章目录 Mysql-root高权限读写注入PostgreSQL——dba高权限读写注入Mssql-sa高权限读写注入 Access无高权限注入点——只能猜解,而且是暴力猜解; MYSQL,PostgreSQL,MSSQL(SQL server)高权限注入点——可升级读写(文件…...

【第5期】前端Vue使用Proxy+Vuex(store、mutations、actions)跨域调通本地后端接口
本期简介 本期要点 本地开发前后端如何跨域调用全局请求、响应处理拦截器处理封装HTTP请求模块编写API请求映射到后端API数据的状态管理 一、 本地开发前后端如何跨域调用 众所周知,只要前端和后端的域名或端口不一样,就存在跨域访问,例如&…...
编译器中,Release和Debug区别)
在Visual Studio(VS)编译器中,Release和Debug区别
一、 优化级别 1、Debug(调试) 在Debug模式下,编译器不会对代码进行优化,而是专注于生成易于调试的代码。这使得开发者可以在调试过程中更直观地跟踪变量的值和程序的执行流程。 2、Release(发布) 在Relea…...
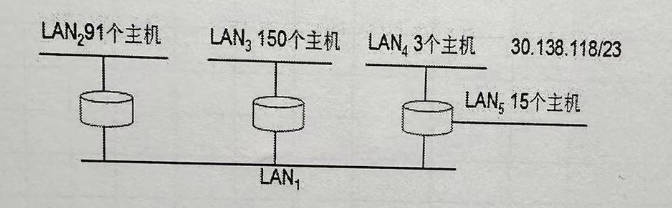
子网划分问题(实战超详解)_主机分配地址
文章目录: 子网划分的核心思想 第一步,考虑借几位作为子网号 第二步,确定子网的网络地址 第三步,明确网络地址,广播地址,可用IP地址范围 一些可能出现的疑问 实战 题目一 子网划分的核心思想 网络号不变,借用主机号来产生新的网络 划分前的网络:网络号主机号 划分后的网络:原网…...

【QT】单例模式,Q_GLOBAL_STATIC 宏的使用和使用静态成员函数,eg:{简单的日志记录器}
简单的日志记录器为例 。 创建一个Logger类,该类负责记录应用程序的日志消息 使用 Q_GLOBAL_STATIC 宏 解析:Q_GLOBAL_STATIC 是一个 Qt 宏,用于创建全局静态实例。它确保在需要时只创建一次实例,而不管该实例是在哪个线程中创建…...

利用小红书笔记详情API:构建高效的内容创作与运营体系
随着社交媒体的兴起,小红书作为国内知名的内容分享平台,吸引了大量用户和内容创作者。为了更好地获取小红书上的优质内容,许多企业和开发者选择使用小红书笔记详情API。本文将探讨如何利用该API构建高效的内容创作与运营体系。 一、小红书笔记…...

未来机器人的大脑:如何用神经网络模拟器实现更智能的决策?
编辑:陈萍萍的公主一点人工一点智能 未来机器人的大脑:如何用神经网络模拟器实现更智能的决策?RWM通过双自回归机制有效解决了复合误差、部分可观测性和随机动力学等关键挑战,在不依赖领域特定归纳偏见的条件下实现了卓越的预测准…...

React 第五十五节 Router 中 useAsyncError的使用详解
前言 useAsyncError 是 React Router v6.4 引入的一个钩子,用于处理异步操作(如数据加载)中的错误。下面我将详细解释其用途并提供代码示例。 一、useAsyncError 用途 处理异步错误:捕获在 loader 或 action 中发生的异步错误替…...

HTML 语义化
目录 HTML 语义化HTML5 新特性HTML 语义化的好处语义化标签的使用场景最佳实践 HTML 语义化 HTML5 新特性 标准答案: 语义化标签: <header>:页头<nav>:导航<main>:主要内容<article>&#x…...

linux之kylin系统nginx的安装
一、nginx的作用 1.可做高性能的web服务器 直接处理静态资源(HTML/CSS/图片等),响应速度远超传统服务器类似apache支持高并发连接 2.反向代理服务器 隐藏后端服务器IP地址,提高安全性 3.负载均衡服务器 支持多种策略分发流量…...

【力扣数据库知识手册笔记】索引
索引 索引的优缺点 优点1. 通过创建唯一性索引,可以保证数据库表中每一行数据的唯一性。2. 可以加快数据的检索速度(创建索引的主要原因)。3. 可以加速表和表之间的连接,实现数据的参考完整性。4. 可以在查询过程中,…...

STM32标准库-DMA直接存储器存取
文章目录 一、DMA1.1简介1.2存储器映像1.3DMA框图1.4DMA基本结构1.5DMA请求1.6数据宽度与对齐1.7数据转运DMA1.8ADC扫描模式DMA 二、数据转运DMA2.1接线图2.2代码2.3相关API 一、DMA 1.1简介 DMA(Direct Memory Access)直接存储器存取 DMA可以提供外设…...

三体问题详解
从物理学角度,三体问题之所以不稳定,是因为三个天体在万有引力作用下相互作用,形成一个非线性耦合系统。我们可以从牛顿经典力学出发,列出具体的运动方程,并说明为何这个系统本质上是混沌的,无法得到一般解…...

图表类系列各种样式PPT模版分享
图标图表系列PPT模版,柱状图PPT模版,线状图PPT模版,折线图PPT模版,饼状图PPT模版,雷达图PPT模版,树状图PPT模版 图表类系列各种样式PPT模版分享:图表系列PPT模板https://pan.quark.cn/s/20d40aa…...

安宝特案例丨Vuzix AR智能眼镜集成专业软件,助力卢森堡医院药房转型,赢得辉瑞创新奖
在Vuzix M400 AR智能眼镜的助力下,卢森堡罗伯特舒曼医院(the Robert Schuman Hospitals, HRS)凭借在无菌制剂生产流程中引入增强现实技术(AR)创新项目,荣获了2024年6月7日由卢森堡医院药剂师协会࿰…...

三分算法与DeepSeek辅助证明是单峰函数
前置 单峰函数有唯一的最大值,最大值左侧的数值严格单调递增,最大值右侧的数值严格单调递减。 单谷函数有唯一的最小值,最小值左侧的数值严格单调递减,最小值右侧的数值严格单调递增。 三分的本质 三分和二分一样都是通过不断缩…...
