【动态规划】【字符串】C++算法:正则表达式匹配
作者推荐
视频算法专题
涉及知识点
动态规划 字符串
LeetCode10:正则表达式匹配
给你一个字符串 s 和一个字符规律 p,请你来实现一个支持 ‘.’ 和 ‘’ 的正则表达式匹配。
‘.’ 匹配任意单个字符
'’ 匹配零个或多个前面的那一个元素
所谓匹配,是要涵盖 整个 字符串 s的,而不是部分字符串。
示例 1:
输入:s = “aa”, p = “a”
输出:false
解释:“a” 无法匹配 “aa” 整个字符串。
示例 2:
输入:s = “aa”, p = “a*”
输出:true
解释:因为 ‘’ 代表可以匹配零个或多个前面的那一个元素, 在这里前面的元素就是 ‘a’。因此,字符串 “aa” 可被视为 ‘a’ 重复了一次。
示例 3:
输入:s = “ab”, p = "."
输出:true
解释:"." 表示可匹配零个或多个('’)任意字符(‘.’)。
提示:
1 <= s.length <= 20
1 <= p.length <= 20
s 只包含从 a-z 的小写字母。
p 只包含从 a-z 的小写字母,以及字符 . 和 *。
保证每次出现字符 * 时,前面都匹配到有效的字符
动态规划
时间复杂度😮(nnm) n=s.length m = p.length
| 动态规划的状态表示 | p[0,i)和s[0,j)能完全匹配,记录所有(i,j) |
| 动态规划的状态转移方程 | 如果p[i+1]是*,则p[i,i+2)能否匹配s[j,x);否则p[i]能否匹配s[j] |
| 动态规划的的初始化 | {0,0} |
| 动态规划的填表顺序 | 从小到枚举i |
| 动态规划的返回值 | 是否存在状态(p.length,s.lenght) |
滚动哈希集合
转移状态时:只需要读取j1的相关状态,写人j1+1的状态。我们用两个哈希来表示状态:pre表示j1 相关状态,dp 表示j2的相关状态,然后swap。
分类讨论
| .* | [min(pre),s.length) |
| 字母x* | iPre, 如果s[iPre,pPre+y]都是x ,则[iPre+1,iPre+1+y]都是合法状态 iPre取自pre |
| 字母x | s[j]==x,则j+1也是合法状态 |
| . | s[j]存在,j+1就是合法状态 |
代码
核心代码
class Solution {
public:bool isMatch(string s, string p) {m_c = s.length();unordered_set<int> pre = { 0 };for (int i = 0 ; i < p.length(); i++ ){ const auto& ch = p[i];if ('*' == ch){continue;}unordered_set<int> dp;if ((i + 1 < p.length()) && ('*' == p[i + 1])){if ('.' == ch){int iMin = INT_MAX;for (const auto& iPre : pre){iMin = min(iMin, iPre);}for (; iMin <= m_c; iMin++){dp.insert(iMin);}}else{dp = pre;for (const auto& iPre : pre){int j = iPre;while (j < m_c){if (s[j] == ch){dp.insert(++j);}else{break;}}}}}else{for (const auto& iPre : pre){if (iPre < m_c){if (('.' == ch) || (s[iPre] == ch)){dp.insert(iPre + 1);}}}} pre.swap(dp);}return pre.count(m_c);}int m_c;
};
测试用例
template<class T>
void Assert(const T& t1, const T& t2)
{assert(t1 == t2);
}template<class T>
void Assert(const vector<T>& v1, const vector<T>& v2)
{if (v1.size() != v2.size()){assert(false);return;}for (int i = 0; i < v1.size(); i++){Assert(v1[i], v2[i]);}
}int main()
{string s, p;{Solution sln;s = "aa", p = "a";auto res = sln.isMatch(s, p);Assert(false, res);}{Solution sln;s = "aa", p = "aa";auto res = sln.isMatch(s, p);Assert(true, res);}{Solution sln;s = "a", p = "a*";auto res = sln.isMatch(s, p);Assert(true, res);}{Solution sln;s = "aa", p = "a*";auto res = sln.isMatch(s, p);Assert(true, res);}{Solution sln;s = "aaa", p = "a*";auto res = sln.isMatch(s, p);Assert(true, res);}{Solution sln;s = "ab", p = ".*";auto res = sln.isMatch(s, p);Assert(true, res);}{Solution sln;s = "aab", p = "c*a*b";auto res = sln.isMatch(s, p);Assert(true, res);}{Solution sln;s = "aaaaaaaaaaaaab", p = "a*a*a*a*a*a*a*a*a*a*";auto res = sln.isMatch(s, p);Assert(false, res);}
}
动态规划的优化
时间复杂度😮(nm)
优化动态规划的转移方程,改成枚举s。也要处理匹配多个的问题。比如:连续多个不匹配任何字符。
不用滚动哈希集合了。
| 动态规划的状态表示 | p[0,i)和s[0,j)能完全匹配,dp[i][j]为true;否则为false |
| 动态规划的状态转移方程 | 比较复杂下文讨论 |
| 动态规划的的初始化 | dp[0][0]=ture,其它false dp[x][0]也要计算 |
| 动态规划的填表顺序 | 从小到枚举i |
| 动态规划的返回值 | dp[p.length][s.length] |
如果p[i-1]是星号,只需要考虑两种情况:
- 匹配0个字符,dp[i][j] = dp[i-2][j]。
- 匹配n个字符,n>0。 dp[i][j] = dp[i][j-1]
注意
dp[0][x] x>0,无意义全部为false。
dp[x][0] x>0 如果p[0,x)全部是yyyy… ,则为true。 y表示.或字母,两个y可能不相同。
y* 必须处理号,不能处理y,否则如果以号结束的时候,会出错。
动态规划的无后效性
计算dp[i][j]的时候,用到了i,i-1,i-2,j,j-1。 第一层循环从小到大枚举i,第二层循环从小到大枚举j。i小的先处理,i相等的,j小的先处理。
代码
class Solution {
public:bool isMatch(string s, string p) {m_r = p.length();m_c = s.length();vector<vector<bool>> dp(m_r+1, vector<bool>(m_c+1));dp[0][0] = true; for (int i = 1; (i < m_r)&&('*'== p[i]); i+=2 ){dp[i + 1][0] = dp[i - 1][0];}for (int i = 1; i <= m_r; i++){auto Match = [&p, &s](int i,int j) {return ('.' == p[i]) || (s[j] == p[i]); };if ((i < m_r) && ('*' == p[i])){continue;//x* 在*号那处理}for (int j = 1; j <= m_c; j++){ if ('*' == p[i-1]){if (i >= 2){//匹配0个字符dp[i][j] = dp[i][j] | dp[i - 2][j];}if (!Match(i - 2, j-1)){continue;}dp[i][j] = dp[i][j] | dp[i][j-1];//dp[i][j-1] 的*号,可能匹配了0次,1次,2次...}else{if (!Match(i-1, j-1)){continue;}dp[i][j] = dp[i - 1][j - 1];}}}return dp[m_r][m_c];}int m_r, m_c;
};
2022年12月旧版
class Solution {
public:
bool isMatch(string s, string p) {
const int lenS = s.size();
const int lenP = p.size();
//dp[i][j]表示 p的前i个字符能否和s的前j个字符匹配
vector<vector> dp;
dp.assign(lenP + 1, vector(lenS + 1));
dp[0][0] = true;
for (int i = 1; i <= lenP; i++)
{
for (int j = 0; j <= lenS; j++)
{
if (‘’ == p[i-1])
{
if (dp[i -2][j ])
{//匹配0个字符
dp[i ][j ] = true;
}
if (0 == j)
{
continue;
}
if (IsSame(p[i - 2], s[j-1]))
{
//匹配一次和匹配多次
if (dp[i - 2][j] || dp[i ][j-1])
{
dp[i][j] = true;
}
}
}
if (0 == j)
{
continue;
}
if ((i < lenP) && ('’ == p[i ]))
{
//dp[i + 1 + 1][j + 1] != dp[i][j];
}
else
{
if (IsSame(p[i-1], s[j-1]) && dp[i-1][j-1] )
{
dp[i][j] = true;
}
}
}
}
return dp[lenP][lenS];
}
bool IsSame(const char& ch1, const char& ch2)
{
return (‘.’ == ch1) || (‘.’ == ch2) | (ch1 == ch2);
}
};

扩展阅读
视频课程
有效学习:明确的目标 及时的反馈 拉伸区(难度合适),可以先学简单的课程,请移步CSDN学院,听白银讲师(也就是鄙人)的讲解。
https://edu.csdn.net/course/detail/38771
如何你想快
速形成战斗了,为老板分忧,请学习C#入职培训、C++入职培训等课程
https://edu.csdn.net/lecturer/6176
相关下载
想高屋建瓴的学习算法,请下载《喜缺全书算法册》doc版
https://download.csdn.net/download/he_zhidan/88348653
| 我想对大家说的话 |
|---|
| 闻缺陷则喜是一个美好的愿望,早发现问题,早修改问题,给老板节约钱。 |
| 子墨子言之:事无终始,无务多业。也就是我们常说的专业的人做专业的事。 |
| 如果程序是一条龙,那算法就是他的是睛 |
测试环境
操作系统:win7 开发环境: VS2019 C++17
或者 操作系统:win10 开发环境: VS2022 C++17
如无特殊说明,本算法用**C++**实现。

相关文章:

【动态规划】【字符串】C++算法:正则表达式匹配
作者推荐 视频算法专题 涉及知识点 动态规划 字符串 LeetCode10:正则表达式匹配 给你一个字符串 s 和一个字符规律 p,请你来实现一个支持 ‘.’ 和 ‘’ 的正则表达式匹配。 ‘.’ 匹配任意单个字符 ’ 匹配零个或多个前面的那一个元素 所谓匹配,是…...

fgetc_fgets_getc_getchar
一、fgetc 1、从流中读取下一个字符 下一个的意思是紧跟在指针后面的,对于一个刚打开文件的流,指针在文件的最前面,它的下一个字符就是文件的第一个字符。读完第一个字符后,指针就会走到第一个字符后面,这时它的下一个…...
12.30_黑马数据结构与算法笔记Java
目录 320 全排列无重复 Leetcode47 321 组合 Leetcode77 分析 322 组合 Leetcode77 实现 323 组合 Leetcode77 剪枝 324 组合之和 Leetcode 39 325 组合之和 Leetcode 40 326 组合之和 Leetcode 216 327 N皇后 Leetcode51-1 328 N皇后 Leetcode51-2 329 解数独 Leetco…...

【电路笔记】-电容分压器
电容分压器 文章目录 电容分压器1、概述2、串联电容器的电压分布3、电容分压器示例14、电容分压器示例2 分压器电路可以由电抗元件构成,就像由固定值电阻器构成一样容易。 1、概述 但就像电阻电路一样,电容分压器网络即使使用属于电抗元件的电容器&…...

线性代数基础知识
计算机视觉一些算法中常会用到线性代数的一些知识,为了便于理解和快速回忆,博主这边对常用的一些知识点做下整理,主要来源于如下这本书籍。 1. 矩阵不仅仅是数字排列而已,不然也不会有那么大精力研究它。其可以表示一种映射 关于…...

Linux Shell 016-文本比较工具diff
Linux Shell 016-文本比较工具diff 本节关键字:Linux、Bash Shell、文本比较 相关指令:diff、cat、patch diff介绍 diff工具用于逐行比较文件的不同,如果指定要比较目录,则diff会比较目录中相同文件名的文件,但不会…...
)
八股文打卡day13——计算机网络(13)
面试题:DNS是什么?DNS的查询过程是什么? 我的回答: 我来讲一下我对DNS的理解 DNS是域名系统,它是一个域名和IP地址相互映射的数据库。通过DNS,可以将我们浏览器中输入的域名,例如:…...

android studio导入module
在Android Studio中导入一个Module(模块),可以按照以下步骤进行操作: 打开Android Studio,并打开你的项目。在菜单栏中,点击 "File"(文件)-> "New"…...
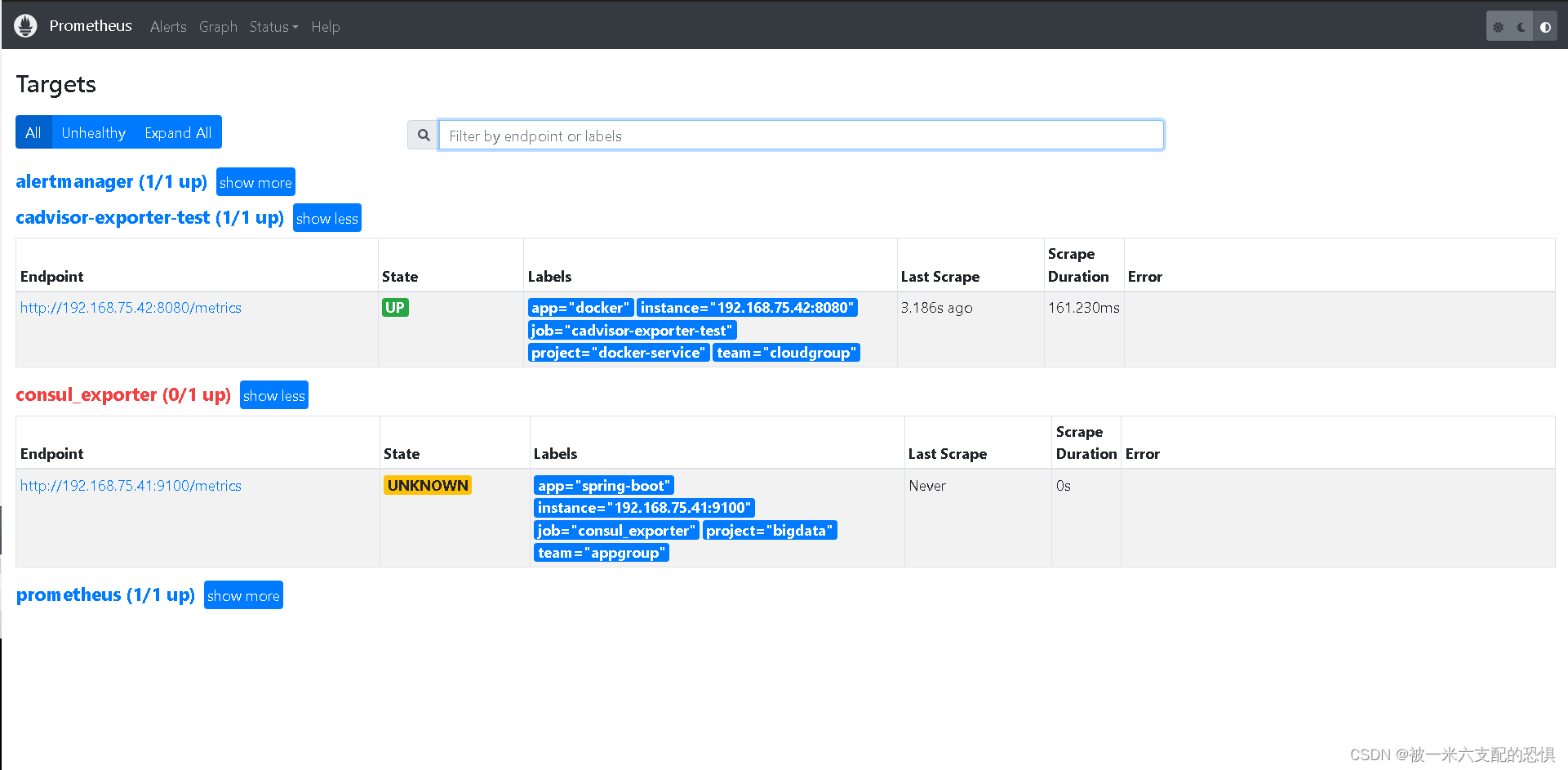
Prometheus通过consul实现自动服务发现
环境,软件准备 本次演示环境,我是在虚拟机上安装 Linux 系统来执行操作,以下是安装的软件及版本: System: CentOS Linux release 7.6Docker: 24.0.5Prometheus: v2.37.6Consul: 1.6.1 注意:这里为了方便启动 Prometheus、Consul服…...

c++11--原子操作,顺序一致性,内存模型
1.原子操作 多线程下为了实现对临界区资源的互斥访问,最普遍的方式是使用互斥锁保护临界区。 然而,如果临界区资源仅仅是数值类型时,对这些类型c提供了原子类型,通过使用原子类型可以更简洁的获得互斥保护的支持。 (1). 一个实例…...
【数据结构】栈和队列(队列的基本操作和基础知识)
🌈个人主页:秦jh__https://blog.csdn.net/qinjh_?spm1010.2135.3001.5343🔥 系列专栏:《数据结构》https://blog.csdn.net/qinjh_/category_12536791.html?spm1001.2014.3001.5482 目录 前言 队列 队列的概念和结构 队列的…...
设计模式——适配器模式(Adapter Pattern)
概述 适配器模式可以将一个类的接口和另一个类的接口匹配起来,而无须修改原来的适配者接口和抽象目标类接口。适配器模式(Adapter Pattern):将一个接口转换成客户希望的另一个接口,使接口不兼容的那些类可以一起工作,其别名为包装…...
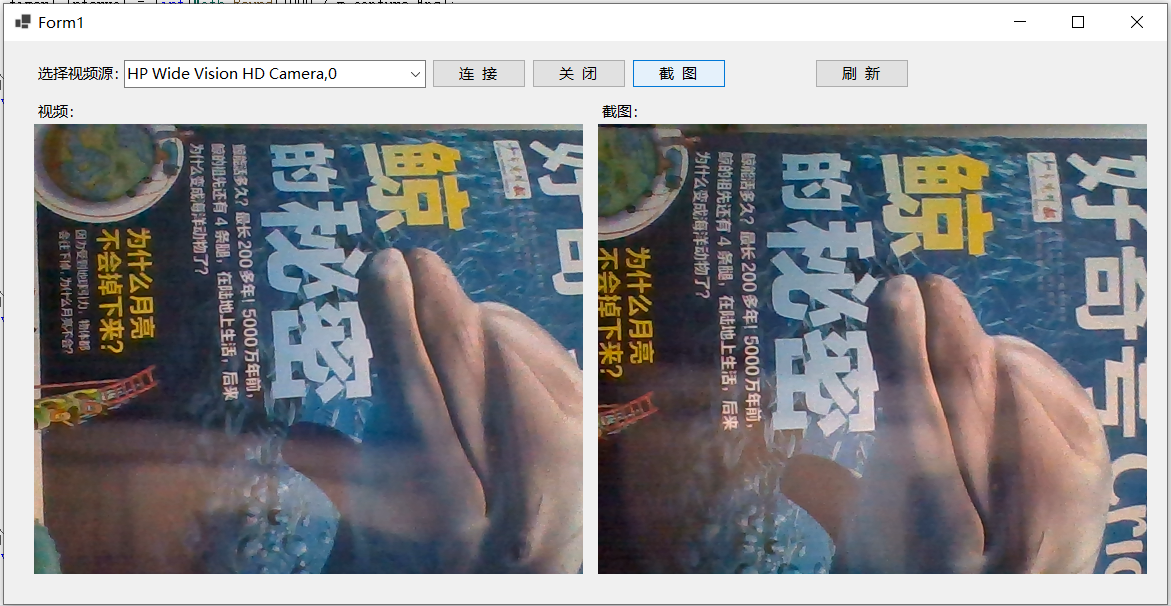
测试C#使用OpenCvSharp从摄像头获取图片
OpenCvSharp也支持获取摄像头数据,不同于之前测试AForge时使用AForge控件显示摄像头数据流并从中截图图片,OpenCvSharp中显示摄像头数据流需要周期性地从摄像头中截取图片并显示在指定控件中。本文学习C#使用OpenCvSharp从摄像头获取图片的基本方式。 …...
【基础】【Python网络爬虫】【12.App抓包】reqable 安装与配置(附大量案例代码)(建议收藏)
Python网络爬虫基础 App抓包1. App爬虫原理2. reqable 的安装与配置reqable 安装教程reqable 的配置 3. 模拟器的安装与配置夜神模拟器的安装夜神模拟器的配置配置代理配置证书 4. 内联调试及注意事项软件启动顺开启抓包功reqable面板功列表部件功能列表数据快捷操作栏 夜神模拟…...
LabVIEW在电机噪声与振动探测的应用
LabVIEW在电机噪声与振动探测的应用 硬件部分是电机噪声和振动测试分析系统的基础,主要由三大核心组件构成:高灵敏度振动传感器、先进的信号调理电路和高性能数据采集卡。这些设备协同工作,确保了从电机捕获的噪声和振动信号的准确性和可靠性…...

编码器是什么,以光电编码器为例,说明一下光电编码器的名字由来,结构,原理,特点,用处
问题描述: 问题解答: 定义:编码器是一种测量角度、位置、速度等物理量的传感器,它可以将物理量转换成电信号,以便计算机或控制系统进行处理和控制。编码器通常由码盘和光电转换器组成,码盘上刻有若干条码道…...

MySQL:主从复制
准备两台服务器:安装好mysql mysql1:192.168.2.222 master mysql2:192.168.2.226 slave 1、主从服务器分别作以下 1.1、版本一致 1.2、初始化表,并在后台启动mysql 1.3、修改root的密码 2、修改主服务器master #vi /etc/my…...
【K8S 二进制部署】部署Kurbernetes的网络组件、高可用集群、相关工具
目录 一、K8S的网络类型: 1、K8S中的通信模式: 1.1、、pod内部之间容器与容器之间的通信 1.2、同一个node节点之内,不同pod之间的通信方式: 1.3、不同node节点上的pod之间是如何通信的呢? 2、网络插件一ÿ…...

Ubuntu 常用命令之 locate 命令用法介绍
🔥Linux/Ubuntu 常用命令归类整理 locate命令是在Ubuntu系统下用于查找文件或目录的命令。它使用一个预先构建的数据库(通常由updatedb命令创建)来查找文件或目录,因此它的查找速度非常快。 plocate 安装 locate 不是 Ubuntu 系统的原生命令/功能,要想在 Ubuntu 系统中…...

java中file类常用方法举例说明
java中file类常用方法举例说明 当使用 java.io.File 类时,以下是一些常用方法的举例说明: 创建文件或目录: // 使用路径名创建File实例 File file new File("C:\\Users\\UserName\\Documents\\example.txt");// 使用父路径和子路…...

.Net框架,除了EF还有很多很多......
文章目录 1. 引言2. Dapper2.1 概述与设计原理2.2 核心功能与代码示例基本查询多映射查询存储过程调用 2.3 性能优化原理2.4 适用场景 3. NHibernate3.1 概述与架构设计3.2 映射配置示例Fluent映射XML映射 3.3 查询示例HQL查询Criteria APILINQ提供程序 3.4 高级特性3.5 适用场…...

Swift 协议扩展精进之路:解决 CoreData 托管实体子类的类型不匹配问题(下)
概述 在 Swift 开发语言中,各位秃头小码农们可以充分利用语法本身所带来的便利去劈荆斩棘。我们还可以恣意利用泛型、协议关联类型和协议扩展来进一步简化和优化我们复杂的代码需求。 不过,在涉及到多个子类派生于基类进行多态模拟的场景下,…...

蓝牙 BLE 扫描面试题大全(2):进阶面试题与实战演练
前文覆盖了 BLE 扫描的基础概念与经典问题蓝牙 BLE 扫描面试题大全(1):从基础到实战的深度解析-CSDN博客,但实际面试中,企业更关注候选人对复杂场景的应对能力(如多设备并发扫描、低功耗与高发现率的平衡)和前沿技术的…...

对WWDC 2025 Keynote 内容的预测
借助我们以往对苹果公司发展路径的深入研究经验,以及大语言模型的分析能力,我们系统梳理了多年来苹果 WWDC 主题演讲的规律。在 WWDC 2025 即将揭幕之际,我们让 ChatGPT 对今年的 Keynote 内容进行了一个初步预测,聊作存档。等到明…...

大模型多显卡多服务器并行计算方法与实践指南
一、分布式训练概述 大规模语言模型的训练通常需要分布式计算技术,以解决单机资源不足的问题。分布式训练主要分为两种模式: 数据并行:将数据分片到不同设备,每个设备拥有完整的模型副本 模型并行:将模型分割到不同设备,每个设备处理部分模型计算 现代大模型训练通常结合…...

JDK 17 新特性
#JDK 17 新特性 /**************** 文本块 *****************/ python/scala中早就支持,不稀奇 String json “”" { “name”: “Java”, “version”: 17 } “”"; /**************** Switch 语句 -> 表达式 *****************/ 挺好的ÿ…...

多种风格导航菜单 HTML 实现(附源码)
下面我将为您展示 6 种不同风格的导航菜单实现,每种都包含完整 HTML、CSS 和 JavaScript 代码。 1. 简约水平导航栏 <!DOCTYPE html> <html lang"zh-CN"> <head><meta charset"UTF-8"><meta name"viewport&qu…...
可以参考以下方法:)
根据万维钢·精英日课6的内容,使用AI(2025)可以参考以下方法:
根据万维钢精英日课6的内容,使用AI(2025)可以参考以下方法: 四个洞见 模型已经比人聪明:以ChatGPT o3为代表的AI非常强大,能运用高级理论解释道理、引用最新学术论文,生成对顶尖科学家都有用的…...
的原因分类及对应排查方案)
JVM暂停(Stop-The-World,STW)的原因分类及对应排查方案
JVM暂停(Stop-The-World,STW)的完整原因分类及对应排查方案,结合JVM运行机制和常见故障场景整理而成: 一、GC相关暂停 1. 安全点(Safepoint)阻塞 现象:JVM暂停但无GC日志,日志显示No GCs detected。原因:JVM等待所有线程进入安全点(如…...

中医有效性探讨
文章目录 西医是如何发展到以生物化学为药理基础的现代医学?传统医学奠基期(远古 - 17 世纪)近代医学转型期(17 世纪 - 19 世纪末)现代医学成熟期(20世纪至今) 中医的源远流长和一脉相承远古至…...
