发表《Nature》！美国研究团队发布可编程逻辑量子处理器
（图片来源：网络）
近期，美国研究团队开发了一款可编程的逻辑量子处理器，并展示了可靠且可扩展的量子计算所需的关键要素，该成果已发表于《Nature》期刊（doi：10.1038/s41586-023-06927-3）。
通过在逻辑量子比特中编码信息，并利用一些物理量子比特来纠正那些限制量子计算机性能的错误，该量子处理器可以执行数百个门操作并运行大规模的量子算法。
从物理量子比特到逻辑量子比特
这一可编程的结构被称为“中性原子阵列”，它由从光镊中捕获的超低温铷原子阵列组成。原子的量子态通过一系列声光偏转器（AOD）控制和操纵，这些偏转器通过可以创建大型可重构的光束网格，来实现量子比特之间的任意连接。实验表明，该系统中的物理量子比特可以被纠缠，以产生低错误率的2个量子比特门操作。
在这项研究中，美国哈佛大学的Mikhail Lukin和他的同事利用光学复用技术从280个物理量子比特中创建了48个逻辑量子比特，相较于其他只创建了2个逻辑量子比特和单个纠缠门的演示，Mikhail Lukin团队的研发成果更具优势。
多路复用方案利用AOD产生光束，照亮单个逻辑单元内的所有物理量子比特，并让这些物理量子比特同时执行相同的操作。
该方法在本质上具有容错性，因为逻辑块中的每个物理量子比特都是独立处理的，所以能够有效防止物理误差转化为逻辑错误。该团队还采用了另一种与该方法类似的策略，成功实现在单个并行步骤中为逻辑量子比特创建容错纠缠门。
保真度从72%提升至99%
研究人员通过利用纠缠门创建基于最大纠缠态（GHZ）的逻辑量子比特的方法进行了测试。实验结果显示，容错算法的保真度高达72%，后处理纠错的保真度则超过了99%。此外，团队还配置了复杂的逻辑电路，用于运行一种特定算法。结果均表明，纠错技术可以提高量子模拟的性能。
Mikhail Lukin对此表示：“我们预计这一新进展将加快大规模实用量子计算机的发展进程。”该团队人员认为，通过优化控制方法并提高激光功率，他们目前的研发结构能够较为容易地扩展至超过10,000个量子比特。
编译：琳梦
编辑：Brightny
特此说明：量子前哨翻译此文仅作信息传递和参考，并不意味着同意此文中的观点与数据。
——end——
欢迎添加我们的微信，加入量子前哨粉丝群
与大家一起探讨交流量子领域动态↓↓↓~~
相关文章：
发表《Nature》！美国研究团队发布可编程逻辑量子处理器
（图片来源：网络） 近期，美国研究团队开发了一款可编程的逻辑量子处理器，并展示了可靠且可扩展的量子计算所需的关键要素，该成果已发表于《Nature》期刊（doi：10.1038/s41586-023-06…...
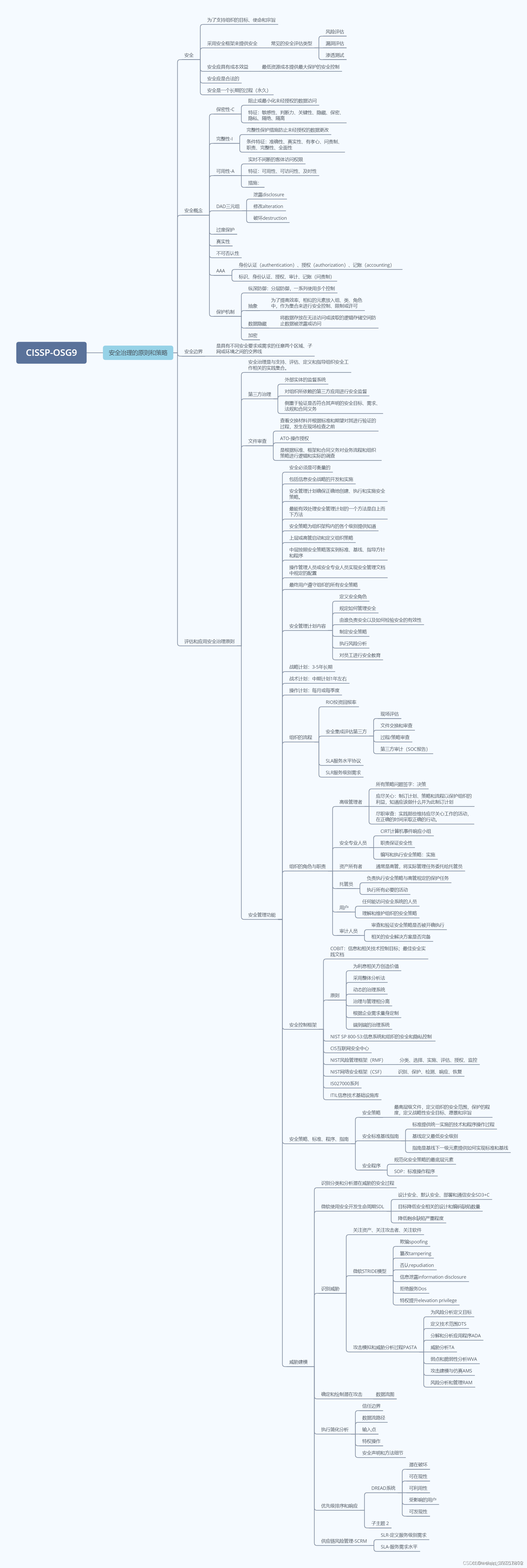
CISSP 第1章：实现安全治理的原则和策略
作者：nothinghappend 链接：https://zhuanlan.zhihu.com/p/669881930 来源：知乎 著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。 CIA CIA 三性： 机密性：和数据泄露有关。完整性…...
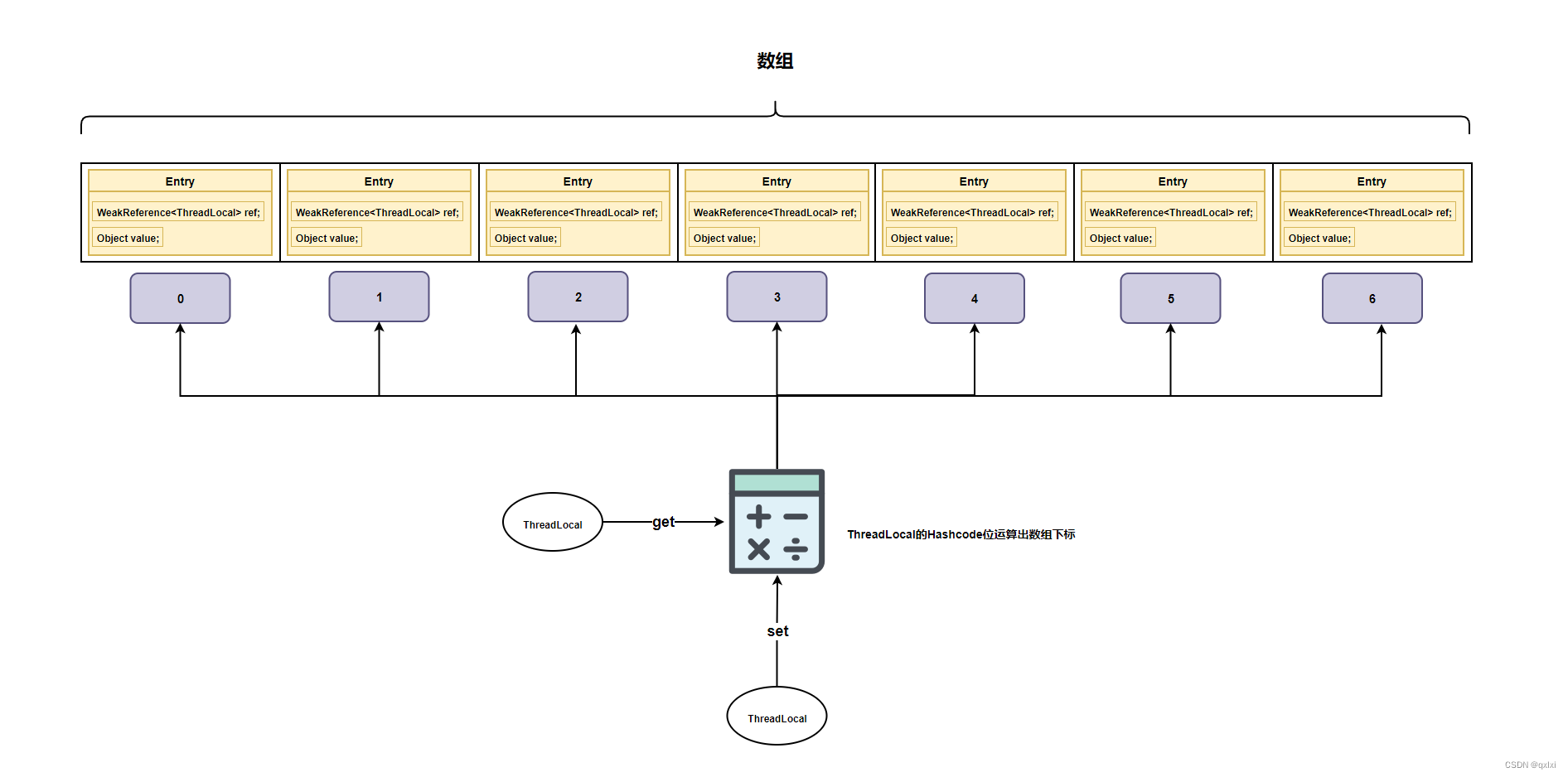
【并发设计模式】聊聊线程本地存储模式如何实现的线程安全
前面两篇文章，通过两阶段终止的模式进行优雅关闭线程，利用数据不变性的方式保证数据安全，以及基于COW的模式，保证读数据的安全。本篇我们来简述下如果利用线程本地存储的方式保证线程安全。 首先一个大前提就是并发问题ÿ…...
边缘计算网关：重新定义物联网数据处理
随着物联网（IoT）设备的爆炸式增长，数据处理和分析的需求也在迅速增加。传统的数据处理方式，将所有数据传输到中心服务器进行处理，不仅增加了网络负担，还可能导致数据延迟和安全问题。因此，边缘计…...
Linux之下载安装
rpm包管理 rpm介绍 rpm用于互联网下载包的打包及安装工具，他包含在某些linux分发版本中。他生成具有.rpm扩展名的文件。RPM是RedHat Package Manager(RedHat软件包管理工具）的缩写，类似windows的steup.exe。 rpm包的查询指令 查询已经安装…...
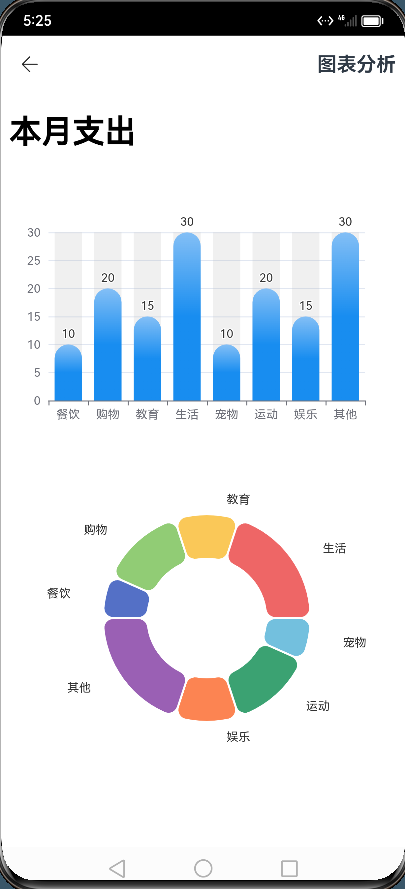
【HarmonyOS开发】案例-记账本开发
OpenHarmony最近一段时间，简直火的一塌糊度，学习OpenHarmony相关的技术栈也有一段时间了，做个记账本小应用，将所学知识点融合记录一下。 1、记账本涉及知识点 基础组件（Button、Select、Text、Span、Divider、Image&am…...
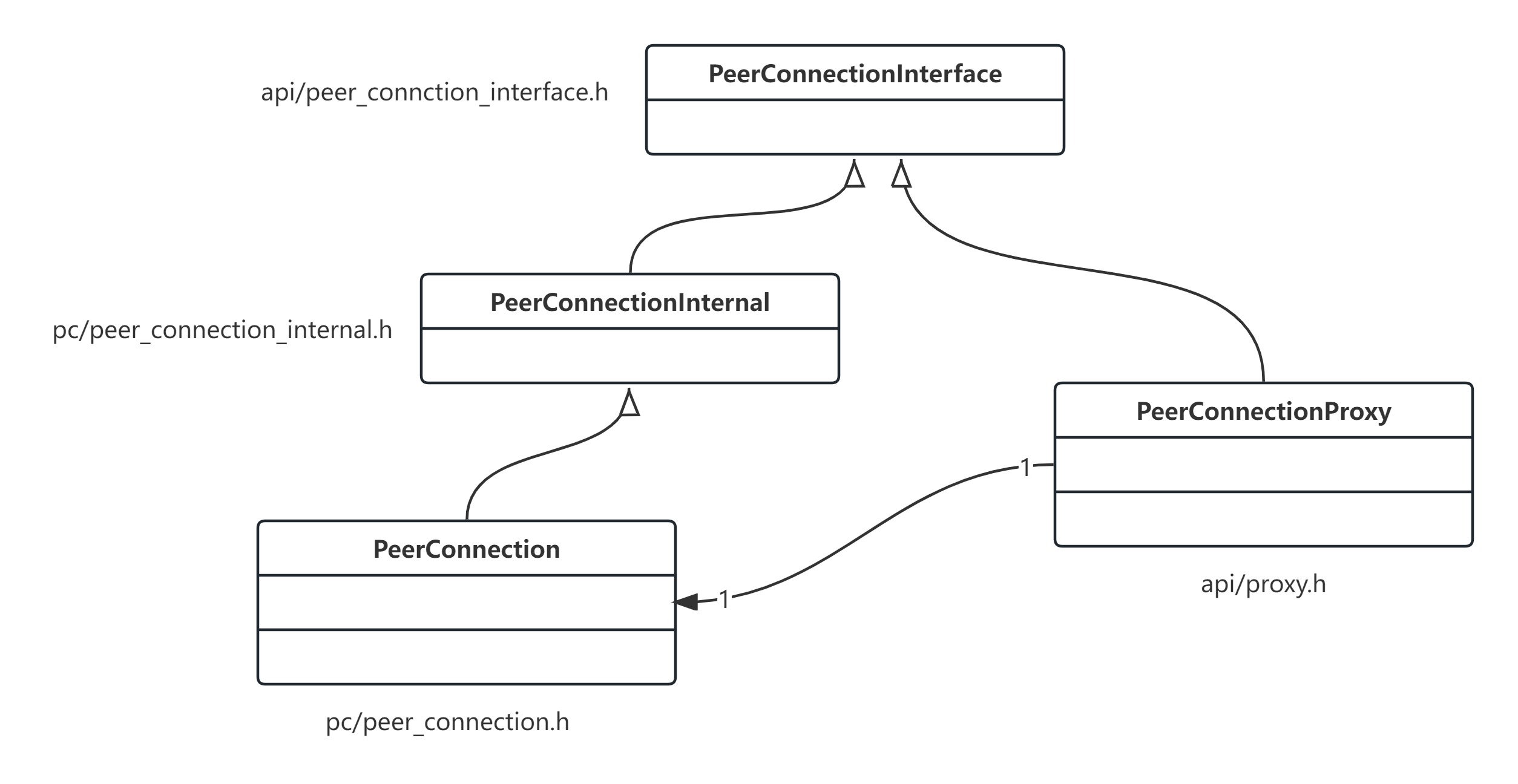
webrtc中的接口代理框架
文章目录 接口代理框架Proxy体系类结构导出接口 webrtc的实际运用PeerConnectionFactoyPeerConnection使用 接口代理框架 webrtc体系庞大，模块化极好，大多数模块都可以独立使用。模块提供接口，外部代码通过接口来使用模块功能。 在webrtc中通…...
【AIGC-图片生成视频系列-4】DreamTuner：单张图像足以进行主题驱动生成
目录 一. 项目概述 问题： 解决： 二. 方法详解 a) 整体结构 b) 自主题注意力 三. 文本控制的动漫角色驱动图像生成的结果 四. 文本控制的自然图像驱动图像生成的结果 五. 姿势控制角色驱动图像生成的结果 2023年的最后一天，发个文记录…...
Jupyter Notebook的10个常用扩展介绍
Jupyter Notebook（前身为IPython Notebook）是一种开源的交互式计算和数据可视化的工具，广泛用于数据科学、机器学习、科学研究和教育等领域。它提供了一个基于Web的界面，允许用户创建和共享文档，这些文档包含实时代码、…...
uniapp项目如何引用安卓原生aar插件（避坑指南三）
官方文档说明：uni小程序SDK 【彩带- 避坑知识点】 如果引用原生aar插件，都配置好之后，云打包，报不包含此插件，除了检查以下步骤流程外，还要检查一下是否上打包的原生插件aar流程有问题。 1.第一步在uniapp项…...
YOLOv8改进 | 检测头篇 | ASFF改进YOLOv8检测头（全网首发）
一、本文介绍 本文给大家带来的改进机制是利用ASFF改进YOLOv8的检测头形成新的检测头Detect_ASFF，其主要创新是引入了一种自适应的空间特征融合方式，有效地过滤掉冲突信息，从而增强了尺度不变性。经过我的实验验证，修改后的检测头…...
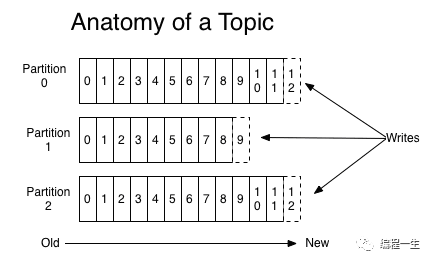
思维训练-怎样设计一个MQ
架构师需要做各种设计，要不断地提高自己的设计能力。这有没有方法可以训练呢？有的，就是看到什么、想到什么，就假设对面坐着产品经理，一起讨论怎么把它设计出来。比如怎样设计一个MQ 我：首先我确认一下需求。…...
RK3399平台入门到精通系列讲解（导读篇）21天挑战Linux系统开发
🚀返回总目录 文章目录 一、关于作者1、博主的联系方式2、支持二、需要具备的知识和工具1、需掌握知识点2、需了解的知识点三、通过系列博客可以学到什么1、本系列博文特色2、21天学习目标3、21天学习内容4、学习时间5、学习产出...
企业微信会话存档sdk报错：A fatal error has been detected by the Java Runtime Environment
错误信息 # A fatal error has been detected by the Java Runtime Environment: # # SIGSEGV (0xb) at pc0x00007f218f93485d, pid10, tid58 # # JRE version: OpenJDK Runtime Environment 18.9 (11.0.14.11) (build 11.0.14.11) # Java VM: OpenJDK 64-Bit Server VM 18.9…...
nginx-docker 搭建websocket反向代理
下载镜像 docker pull nginx复制出配置文件 将/etc/nginx/nginx.conf和/etc/nginx/conf.d/default.conf复制到本机 nginx.conf文件内容 user nginx; worker_processes auto;error_log /var/log/nginx/error.log notice; pid /var/run/nginx.pid;events {worker_c…...
blender插件开发
Quickstart — Blender Python API Blender Python 编程：关键概念 - 知乎 系列目录链接（更新中，如无链接说明未更新） [Blender Python] 列出/插入/删除物体，Blender数据对象 - 知乎 (zhihu.com)[Blender Python] 设…...
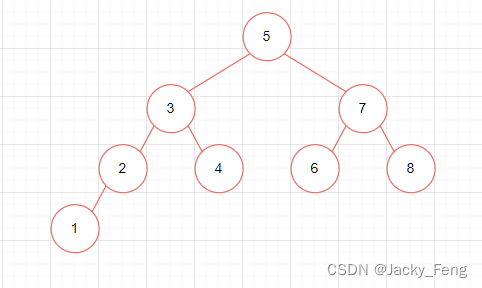
【数据结构】二叉搜索（查找/排序）树
一、二叉搜索树基本概念 1、定义 二叉搜索树，又称为二叉排序树，二叉查找树，它满足如下四点性质： 1）空树是二叉搜索树； 2）若它的左子树不为空，则左子树上所有结点的值均小于它根结…...
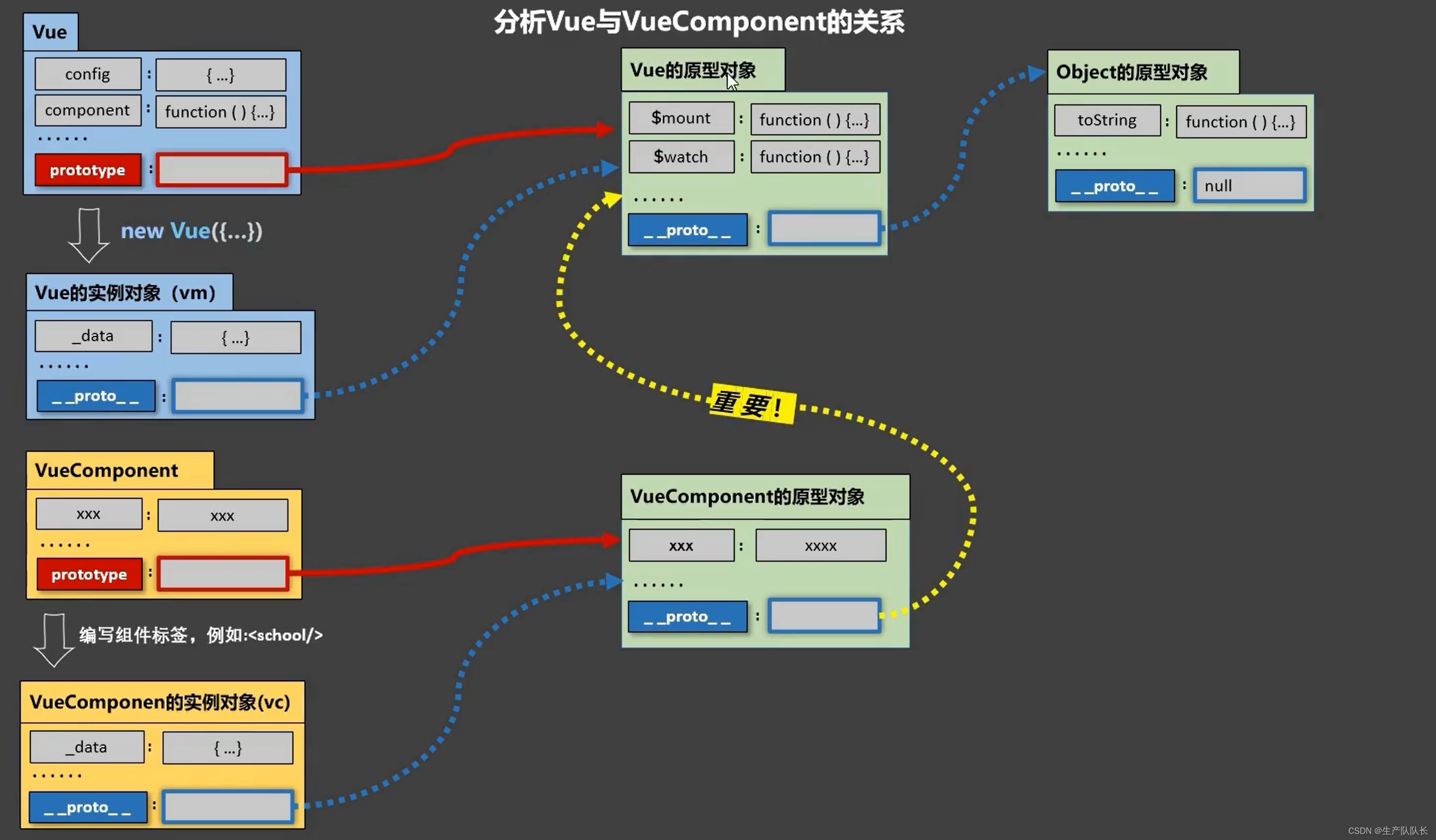
Vue：Vue与VueComponent的关系图
1.一个重要的内置关系：VueComponent.prototype.proto Vue.prototype 2.为什么要有这个关系：让组件实例对象（vc）可以访问到 Vue原型上的属性、方法。 案例证明： <!DOCTYPE html> <html lang"en"&…...
Elasticsearch8集群部署
转载说明：如果您喜欢这篇文章并打算转载它，请私信作者取得授权。感谢您喜爱本文，请文明转载，谢谢。 本文记录在3台服务器上离线搭建es8.7.1版本集群。 1. 修改系统配置 1.1 hosts配置 在三台es节点服务器加入hostname解析&…...
【小白专用】c# 如何获取项目的根目录
1、取得控制台应用程序的根目录方法 方法1、Environment.CurrentDirectory 取得或设置当前工作目录的完整限定路径 方法2、AppDomain.CurrentDomain.BaseDirectory 获取基目录，它由程序集冲突解决程序用来探测程序集 2、取得Web应用程序的根目录方法 方法1、HttpRun…...
【PXIE301-208】基于PXIE总线架构的Serial RapidIO总线通讯协议仿真卡
板卡概述 PXIE301-208是一款基于3U PXIE总线架构的Serial RapidIO总线通讯协议仿真卡。该板卡采用Xilinx的高性能Kintex系列FPGA作为主处理器，实现各个接口之间的数据互联、处理以及实时信号处理。板卡支持4路SFP光纤接口，支持一个PCIe x8主机接口&…...
软件测试/测试开发丨Windows系统chromedriver安装与环境变量配置
一、selenium 环境配置 1、chrome 浏览器的安装与配置 目前比较常用的浏览器是 Google Chrome 浏览器，所以本教程以 chrome 为主，后面简介一下其他浏览器的环境配置。 （1）chrome 下载: www.google.cn/chrome/ （2&a…...
【vim 学习系列文章 3.1 -- vim 删除 ^M】
请阅读【嵌入式开发学习必备专栏 之 VIM 专栏】 文章目录 ^M 来源^M 删除 ^M 来源 在 Vim 中打开文件时，您可能会遇到行尾的 ^M 字符，这通常是因为文件使用了 Windows 风格的回车换行符（CRLF），而不是 Unix/Linux 风格…...
深入理解 C# 中的字符串比较：String.CompareTo vs String.Equals
深入理解 C# 中的字符串比较：String.CompareTo vs String.Equals 在处理字符串时，了解如何正确比较它们对于编写清晰、有效和可靠的 C# 程序至关重要。本文将深入探讨 C# 中的两个常用字符串比较方法：String.CompareTo 和 String.Equals&…...
DevOps持续交付之容器化CICD流水线
DevOps持续交付 随着DevOps⼤规模化的落地和应⽤，持续集成以及持续交付已经是⼀种常态的。CI指的是持续集成，使⽤的开源⼯具是Jenkins，CD指的是持续交付和持续部署，⼀个完整的软件开发⽣命周期为: 主要流程可以具体为: 构建阶段…...
Linux/Unix/国产化操作系统常用命令（二）
目录 后CentOS时代国产化操作系统国产化操作系统有哪些常用Linux命令关于Linux的LOGO 后CentOS时代 在CentOS 8发布后，就有了一些变化和趋势，可以说是进入了"后CentOS时代"。这个时代主要表现在以下几个方面： CentOS Stream的引入…...
基于SpringBoot的智慧生活商城系统
文章目录 项目介绍主要功能截图：部分代码展示设计总结项目获取方式🍅 作者主页：超级无敌暴龙战士塔塔开 🍅 简介：Java领域优质创作者🏆、 简历模板、学习资料、面试题库【关注我，都给你】 🍅文末获取源码联系🍅 项目介绍 基于SpringBoot的智慧生活商城系统,java…...
Vue框架引入Axios
首先已经创建好了 Vue 框架，安装好了 node.js。 没有完成的可按照此博客搭建：搭建Vue项目 之后打开终端，使用命令。 1、命令安装 axios 和 vue-axios npm install axios --save npm install vue-axios --save2、package.json 查看版本 在 p…...
EasyExcel 通过模板 导入、导出、下载模板
EasyExcel 通过模板 导入、导出、下载模板 import lombok.AllArgsConstructor; import lombok.Builder; import lombok.Data; import lombok.NoArgsConstructor;import javax.validation.constraints.NotBlank; import javax.validation.constraints.Pattern; import java.io.…...
SAP ABAP通过代码解锁SM12中被锁定目标＜转载＞（RFC: ENQUEUE_READ和 ENQUE_DELETE）
原文链接：https://blog.csdn.net/sinat_38119716/article/details/121406275 备注 RFC:ENQUEUE_READ 读取的是SM12的数据 RFC:ENQUEUE_READ2 读取的是SMENQ的数据 SM12 和 SMENQ 的数据其实是一样的，只是一个是旧的TCODE 一个是新的 解锁用的都是RFC: …...