Unity中Shader裁剪空间推导(透视相机到裁剪空间的转化矩阵)
文章目录
- 前言
- 一、简单看一下 观察空间—>裁剪空间—>屏幕空间 的转化
- 1、观察空间(右手坐标系、透视相机)
- 2、裁剪空间(左手坐标系、且转化为了齐次坐标)
- 3、屏幕空间(把裁剪坐标归一化设置)
- 4、从观察空间到裁剪空间
- 5、从裁剪空间到屏幕空间后
- 二、透视相机的参数推导
- 1、从XoY平面,求出X~v~从观察空间到裁剪空间的坐标投影 X~p~
- 2、从YoZ平面,求出Y~v~从观察空间到裁剪空间的坐标投影 Y~p~
- 三、把投影到近裁剪面的坐标 归一化设置
- 1、求归一化设置后的 x~n~
- 2、求归一化设置后的 y~n~
- 3、得到最后化简的公式
- 四、构建转化矩阵
- 1、在OpenGL[-1,1]下:
- 2、在DirectX[1,0]下:
- 3、把A、B代入矩阵得
前言
我们把顶点坐标信息转化为裁剪空间。有可能使用到正交相机信息 或 透视相机。我们在这篇文章中,推导一下透视相机视图空间下的坐标转化到裁剪空间的矩阵。

一、简单看一下 观察空间—>裁剪空间—>屏幕空间 的转化

1、观察空间(右手坐标系、透视相机)
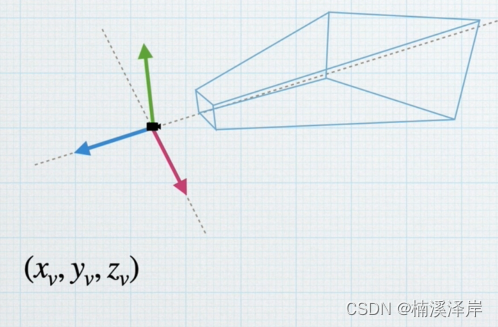
2、裁剪空间(左手坐标系、且转化为了齐次坐标)
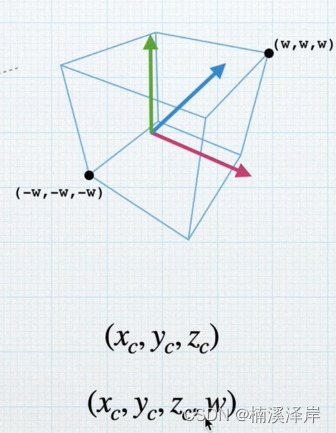
3、屏幕空间(把裁剪坐标归一化设置)

4、从观察空间到裁剪空间
用透视投影矩阵先转化到裁剪空间
然后,在转化为齐次坐标
5、从裁剪空间到屏幕空间后
− 1 ≤ x c w ≤ 1 -1 \leq \frac{x_c}{w}\leq1 −1≤wxc≤1
− w ≤ x c ≤ w -w \leq x_c\leq w −w≤xc≤w
二、透视相机的参数推导
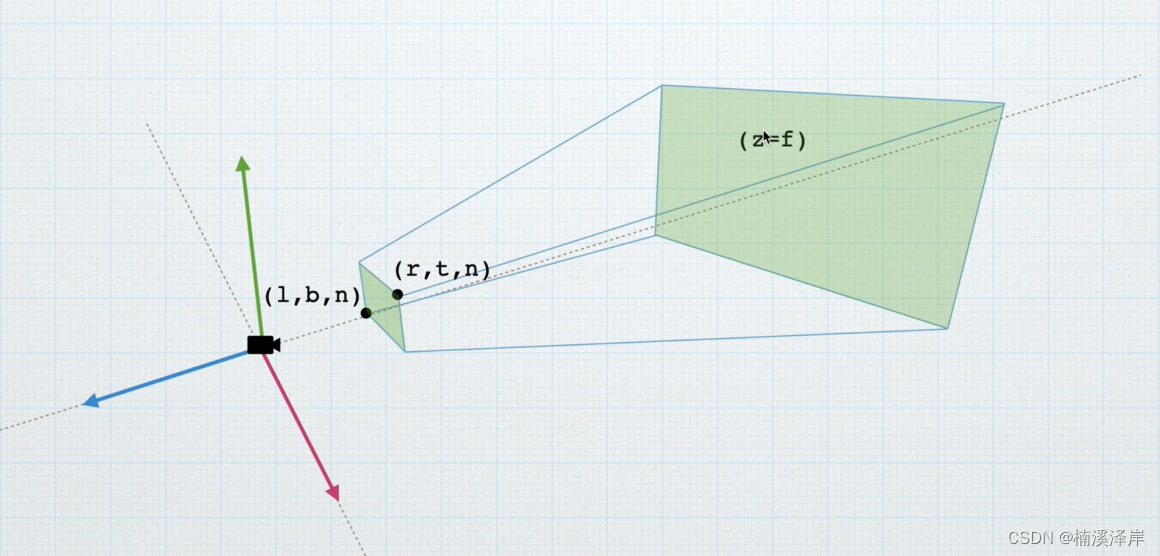
- 我们对于远裁剪面只是已知 f,其他参数都是未知
1、从XoY平面,求出Xv从观察空间到裁剪空间的坐标投影 Xp

- 点 V 是观察空间下的模型顶点,xyz是已知的
已知: ( x v , y v , z v ) 、 − n (x_v,y_v,z_v) 、 -n (xv,yv,zv)、−n - 点P是该点在近裁剪面上的投影点,xyz是未知的
未知: ( x p , y p , z p ) (x_p,y_p,z_p) (xp,yp,zp) - 我们在 XoZ平面上,能求的就是 xp
求: x p x_p xp
z p = − n z_p = -n zp=−n
y p 在 X o Z 平面下,无法计算 y_p 在XoZ平面下,无法计算 yp在XoZ平面下,无法计算
- v点向Z轴做垂线,原点连接v点,围成的两个三角形相似,可得:
x p x v = − n z v \frac{x_p}{x_v} = \frac{-n}{z_v} xvxp=zv−n
x p = − n z v x v x_p = \frac{-n}{z_v} x_v xp=zv−nxv
P = ( − n z v x v , 未知 , − n ) P = (\frac{-n}{z_v}x_v,未知,-n) P=(zv−nxv,未知,−n)
2、从YoZ平面,求出Yv从观察空间到裁剪空间的坐标投影 Yp
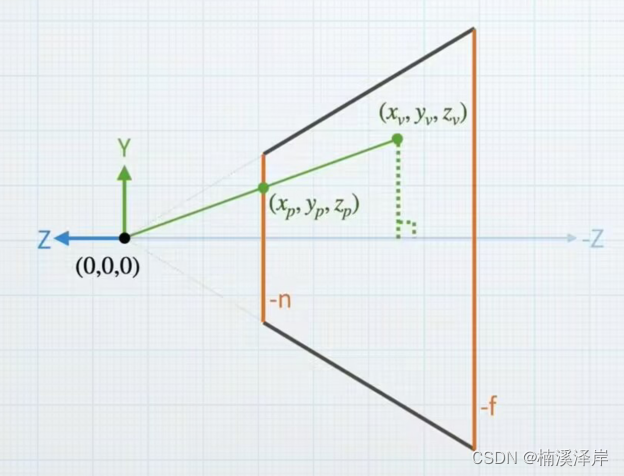
- 点 V 是观察空间下的模型顶点,xyz是已知的
已知: ( x v , y v , z v ) 、 − n (x_v,y_v,z_v) 、 -n (xv,yv,zv)、−n - 点P是该点在近裁剪面上的投影点,xyz是未知的
未知: ( x p , y p , z p ) (x_p,y_p,z_p) (xp,yp,zp) - 我们在 YoZ平面上,能求的就是 yp
求: y p y_p yp
z p = − n z_p = -n zp=−n
x p 在 X o Z 平面下,无法计算 x_p 在XoZ平面下,无法计算 xp在XoZ平面下,无法计算
- v点向Z轴做垂线,原点连接v点,围成的两个三角形相似,可得:
y p y v = − n z v \frac{y_p}{y_v} = \frac{-n}{z_v} yvyp=zv−n
y p = − n z v y v y_p = \frac{-n}{z_v} y_v yp=zv−nyv
P = ( − n z v x v , − n z v y v , − n ) P = (\frac{-n}{z_v}x_v,\frac{-n}{z_v} y_v,-n) P=(zv−nxv,zv−nyv,−n)
三、把投影到近裁剪面的坐标 归一化设置
P = ( − n z v x v , − n z v y v , − n ) P = (\frac{-n}{z_v}x_v,\frac{-n}{z_v} y_v,-n) P=(zv−nxv,zv−nyv,−n)
化到[-1,1]之间
具体参考Unity中Shader裁剪空间推导(正交相机到裁剪空间的转化矩阵)
1、求归一化设置后的 xn
- l ≤ x ≤ r l \leq x \leq r l≤x≤r 化为: − 1 ≤ 2 x w ≤ 1 -1 \leq \frac{2x}{w} \leq 1 −1≤w2x≤1
− 1 ≤ − 2 n x v z v w ≤ 1 -1\leq \frac{-2nx_v}{z_vw}\leq 1 −1≤zvw−2nxv≤1
− 1 ≤ − 2 n w ⋅ x v z v ≤ 1 -1\leq \frac{-2n}{w}·\frac{x_v}{z_v}\leq 1 −1≤w−2n⋅zvxv≤1
2、求归一化设置后的 yn
- l ≤ y ≤ r l \leq y \leq r l≤y≤r 化为: − 1 ≤ 2 y h ≤ 1 -1 \leq \frac{2y}{h} \leq 1 −1≤h2y≤1
− 1 ≤ − 2 n y v z v h ≤ 1 -1\leq\frac{-2ny_v}{z_vh}\leq1 −1≤zvh−2nyv≤1
− 1 ≤ − 2 n h ⋅ y v z v ≤ 1 -1\leq\frac{-2n}{h}·\frac{y_v}{z_v}\leq1 −1≤h−2n⋅zvyv≤1
3、得到最后化简的公式
由于NDC下的坐标由透视除法而得
我们假设透视除法中的 w 为 -zv
还原到裁剪空间还需要乘以 -zv
- X:
− 1 ≤ − 2 n w ⋅ x v z v ≤ 1 -1\leq \frac{-2n}{w}·\frac{x_v}{z_v}\leq 1 −1≤w−2n⋅zvxv≤1
x n = − 2 n w x v z v x_n = \frac{-2n}{w}\frac{x_v}{z_v} xn=w−2nzvxv
− x n z v = 2 n w x v -x_nz_v = \frac{2n}{w}x_v −xnzv=w2nxv
- Y:
− 1 ≤ − 2 n h ⋅ y v z v ≤ 1 -1\leq\frac{-2n}{h}·\frac{y_v}{z_v}\leq1 −1≤h−2n⋅zvyv≤1
y n = − 2 n h y v z v y_n = \frac{-2n}{h}\frac{y_v}{z_v} yn=h−2nzvyv
− y n z v = 2 n h y v -y_n z_v= \frac{2n}{h}y_v −ynzv=h2nyv
- Z:
z n = ? z_n = ? zn=?
− z n z v = − z v ? -z_nz_v = -z_v? −znzv=−zv?
- W:
w = 1 w = 1 w=1
− w n z v = − z v -w_nz_v = -z_v −wnzv=−zv
四、构建转化矩阵
裁剪空间下的点 = 观察空间下的基向量 在 裁剪空间下的矩阵 * 点在观察空间下的坐标
P c = [ V c ] ⋅ P v P_c = [V_c]·P_v Pc=[Vc]⋅Pv
P c = [ C v ] − 1 ⋅ P v P_c = [C_v]^{-1}·P_v Pc=[Cv]−1⋅Pv
P c = [ C v ] T ⋅ P v P_c = [C_v]^{T}·P_v Pc=[Cv]T⋅Pv
- − x n z v = 2 n w x v -x_nz_v = \frac{2n}{w}x_v −xnzv=w2nxv
- − y n z v = 2 n h y v -y_n z_v= \frac{2n}{h}y_v −ynzv=h2nyv
- − z n z v = − z v ? -z_nz_v = -z_v? −znzv=−zv?
- − w n z v = − z v -w_nz_v = -z_v −wnzv=−zv
[ 2 v w 0 ? ? 0 2 n h ? ? 0 0 ? ? 0 0 ? ? ] T = [ 2 v w 0 0 0 0 2 n h 0 0 ? ? ? ? ? ? ? ? ] \begin{bmatrix} \frac{2v}{w} & 0 & ? &?\\ 0 & \frac{2n}{h} & ? &?\\ 0 & 0 & ? &?\\ 0 & 0 & ? & ?\\ \end{bmatrix}^T =\begin{bmatrix} \frac{2v}{w} & 0 & 0 & 0 \\ 0 & \frac{2n}{h} & 0 &0\\ ? & ? & ? &?\\ ? & ? & ? & ?\\ \end{bmatrix} w2v0000h2n00???????? T= w2v0??0h2n??00??00??
[ 2 v w 0 0 0 0 2 n h 0 0 ? ? ? ? ? ? ? ? ] ⋅ [ x v y v z v 1 ] = ( − x n z v , − y n z v , − z n z v , − w n z v ) \begin{bmatrix} \frac{2v}{w} & 0 & 0 & 0 \\ 0 & \frac{2n}{h} & 0 &0\\ ? & ? & ? &?\\ ? & ? & ? & ?\\ \end{bmatrix} · \begin{bmatrix} x_v\\ y_v\\ z_v\\ 1\\ \end{bmatrix} = (-x_nz_v,-y_nz_v,-z_nz_v,-w_nz_v) w2v0??0h2n??00??00?? ⋅ xvyvzv1 =(−xnzv,−ynzv,−znzv,−wnzv)
最后一行由于相乘结果为1可以得出,把最后未知部分设为A,B
[ 2 v w 0 0 0 0 2 n h 0 0 0 0 A B 0 0 − 1 0 ] ⋅ [ x v y v z v 1 ] \begin{bmatrix} \frac{2v}{w} & 0 & 0 & 0 \\ 0 & \frac{2n}{h} & 0 &0\\ 0 & 0 & A &B\\ 0 & 0 & -1 & 0\\ \end{bmatrix} · \begin{bmatrix} x_v\\ y_v\\ z_v\\ 1\\ \end{bmatrix} w2v0000h2n0000A−100B0 ⋅ xvyvzv1
z c = A z v + B z_c = Az_v+B zc=Azv+B
− z n z v = − z v -z_nz_v = -z_v −znzv=−zv
z c − z v = A z v + B − z v \frac{z_c}{-z_v} = \frac{Az_v+B}{-z_v} −zvzc=−zvAzv+B
z n = A z v + B − z v z_n = \frac{Az_v+B}{-z_v} zn=−zvAzv+B
1、在OpenGL[-1,1]下:
z n = A z v + B − z v z_n = \frac{Az_v+B}{-z_v} zn=−zvAzv+B
{ z v = − n , z n = − 1 z v = − f , z n = 1 \begin{cases} z_v = -n,z_n=-1 \\ z_v = -f,z_n = 1 \end{cases} {zv=−n,zn=−1zv=−f,zn=1
{ − 1 = − A n + B n 1 = − A f + B f \begin{cases} -1 = \frac{-An+B}{n}\\ 1 = \frac{-Af + B}{f} \end{cases} {−1=n−An+B1=f−Af+B
{ − n = − A n + B f = − A f + B \begin{cases} -n = -An+B\\ f = -Af + B \end{cases} {−n=−An+Bf=−Af+B
B = A n − n B = An - n B=An−n
f = − A f + A n − n f = -Af +An-n f=−Af+An−n
f + n = A ( n − f ) f + n= A(n-f) f+n=A(n−f)
A = n + f n − f A = \frac{n+f}{n-f} A=n−fn+f
B = n + f n − f n − n B = \frac{n+f}{n-f}n-n B=n−fn+fn−n
B = n 2 + f n n − f n 2 − n f n − f B = \frac{n^2 + fn}{n-f}\frac{n^2-nf}{n-f} B=n−fn2+fnn−fn2−nf
B = 2 n f n − f B = \frac{2nf}{n-f} B=n−f2nf
2、在DirectX[1,0]下:
z n = A z v + B − z v z_n = \frac{Az_v+B}{-z_v} zn=−zvAzv+B
{ z v = − n , z n = 1 z v = − f , z n = 0 \begin{cases} z_v = -n,z_n=1 \\ z_v = -f,z_n = 0 \end{cases} {zv=−n,zn=1zv=−f,zn=0
{ 1 = − A n + B n 0 = − A f + B f \begin{cases} 1 = \frac{-An+B}{n}\\ 0 = \frac{-Af+B}{f} \end{cases} {1=n−An+B0=f−Af+B
{ n = − A n + B 0 = − A f + B \begin{cases} n = -An+B\\ 0 = -Af+B \end{cases} {n=−An+B0=−Af+B
B = A f B = Af B=Af
n = − A n + A f n = -An+Af n=−An+Af
n = A ( f − n ) n = A(f-n) n=A(f−n)
A = n f − n A =\frac{n}{f-n} A=f−nn
B = n f f − n B = \frac{nf}{f-n} B=f−nnf
3、把A、B代入矩阵得
- OpenGL
[ 2 n w 0 0 0 0 2 n h 0 0 0 0 n + f n − f 2 n f n − f 0 0 − 1 0 ] \begin{bmatrix} \frac{2n}{w} & 0 & 0 & 0 \\ 0 & \frac{2n}{h} & 0 &0\\ 0 & 0 & \frac{n+f}{n-f} &\frac{2nf}{n-f}\\ 0 & 0 & -1 & 0\\ \end{bmatrix} w2n0000h2n0000n−fn+f−100n−f2nf0 - DirectX
[ 2 n w 0 0 0 0 2 n h 0 0 0 0 n f − n n f f − n 0 0 − 1 0 ] \begin{bmatrix} \frac{2n}{w} & 0 & 0 & 0 \\ 0 & \frac{2n}{h} & 0 &0\\ 0 & 0 & \frac{n}{f-n} &\frac{nf}{f-n}\\ 0 & 0 & -1 & 0\\ \end{bmatrix} w2n0000h2n0000f−nn−100f−nnf0
相关文章:

Unity中Shader裁剪空间推导(透视相机到裁剪空间的转化矩阵)
文章目录 前言一、简单看一下 观察空间—>裁剪空间—>屏幕空间 的转化1、观察空间(右手坐标系、透视相机)2、裁剪空间(左手坐标系、且转化为了齐次坐标)3、屏幕空间(把裁剪坐标归一化设置)4、从观察空…...

企业签名分发对移动应用开发者有什么影响
企业签名分发是移动应用开发者在应用程序发布前测试、内部分发和特定的受众群体分发等方面比较常用的一种工具。那对于应用商城分发有啥区别,下面简单的探讨一下。 独立分发能力 通过企业签名分发开发者可以自己决定应用程序的发布时间和方式,不用受应用…...
3D游戏角色建模纹理贴图处理
在线工具推荐: 3D数字孪生场景编辑器 - GLTF/GLB材质纹理编辑器 - 3D模型在线转换 - Three.js AI自动纹理开发包 - YOLO 虚幻合成数据生成器 - 三维模型预览图生成器 - 3D模型语义搜索引擎 在本文中,我们将介绍 3D 纹理的基础知识,并讨…...

【C++ 单例模式】
正确的析构 静态实例和回收类 SingletonMode.cpp #include <iostream> #include <pthread.h>class Singleton {private:Singleton(){std::cout << "构造" << std::endl;};~Singleton(){std::cout << "析构" << std::…...

React16源码: ConcurrentMode的使用及源码实现
ConcurrentMode 1 ) 概述 ConcurrentMode 是 React 16 出来的一个最令人振奋的功能在2018年年初是 Async Mode,在发布了16.6之后,名字进行了更新然后改成了 ConcurrentMode,中间的API有一个过渡的版本,后续会提到它其实是 React…...

SQL性能优化-索引
1.性能下降sql慢执行时间长等待时间长常见原因 1)索引失效 索引分为单索、复合索引。 四种创建索引方式 create index index_name on user (name); create index index_name_2 on user(id,name,email); 2)查询语句较烂 3)关联查询太多join&a…...

Ubuntu本地快速搭建web小游戏网站,公网用户远程访问
🔥博客主页: 小羊失眠啦. 🎥系列专栏:《C语言》 《数据结构》 《Linux》《Cpolar》 ❤️感谢大家点赞👍收藏⭐评论✍️ 前些天发现了一个巨牛的人工智能学习网站,通俗易懂,风趣幽默,…...
easyrecovery 2024最新免费密钥分享 实用数据恢复软件分享
在日常使用电脑时,我们经常会遇到误删文件的情况,若文件还未被彻底删除,我们还可以通过电脑中的回收站将其恢复,但若是回收站都被清空的话,想要恢复文件就变得比较困难了,而EasyRecovery可以很好的帮助我们…...

2.4信道复用技术
目录 2.4信道复用技术2.4.1频分复用、时分复用和统计时分复用频分复用FDM(Frequency Division Multiplexing)时分复用TDM(Time Division Multiplexing)统计时分复用STDM(Statistic TDM) 2.4.2波分复用2.4.3…...

JVM篇:JVM的简介
JVM简介 JVM全称为Java Virtual Machine,翻译过来就是java虚拟机,Java程序(Java二进制字节码)的运行环境 JVM的优点: Java最大的一个优点是,一次编写,到处运行。之所以能够实现这个功能就是依…...
uniapp 输入手机号并且正则校验
1.<input input“onInput” :value“phoneNum” type“number” maxlength“11”/> 3. method里面写 onInput(e){ this.phoneNum e.detail.value }, 4.调用接口时候校验正则 if (!/^1[3456789]\d{9}$/.test(this.phoneNum)) {uni.showToast({title: 请输入正确的手机号…...

经典目标检测YOLO系列(一)复现YOLOV1(3)正样本的匹配及损失函数的实现
经典目标检测YOLO系列(一)复现YOLOV1(3)正样本的匹配及损失函数的实现 之前,我们依据《YOLO目标检测》(ISBN:9787115627094)一书,提出了新的YOLOV1架构,并解决前向推理过程中的两个问题,继续按照此书进行YOLOV1的复现。 经典目标…...
kbdnecat.DLL文件缺失,软件或游戏无法启动运营,快速修复方法
“kbdnecat.DLL文件是什么?为什么一起动游戏或软件,Windows就报错“kbdnecat.DLL文件缺失,软件无法启动””,应该怎么修复呢? 首先,先来了解“kbdnecat.DLL文件”是什么? kbdnecat.DLL是一个动…...
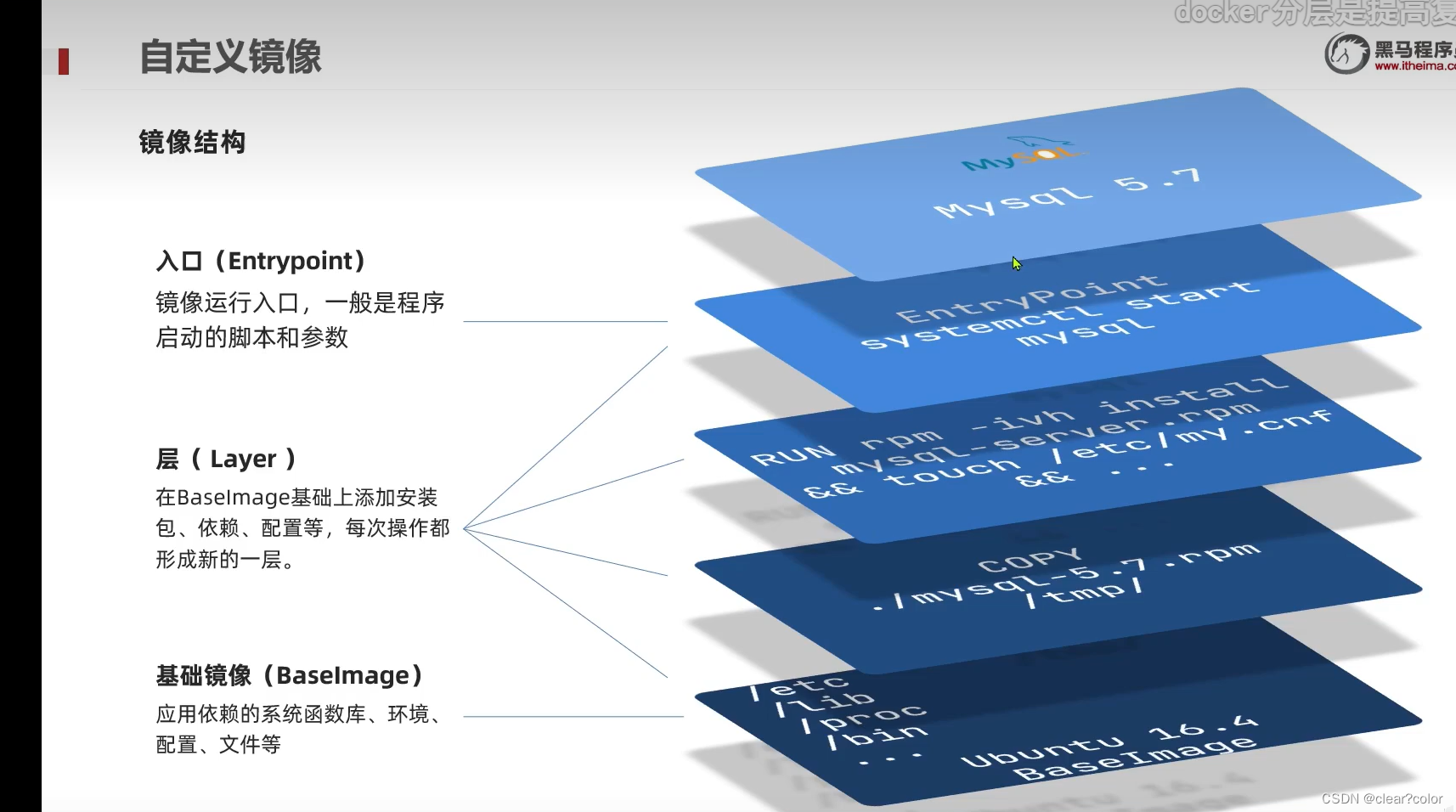
Dockerfile与DockerCompose
Docker的Image结构是怎样的? 镜像是将应用程序 及其需要的 系统函数库、环境、配置、依赖 打包而成。 镜像结构 入口( Entrypoint ) 镜像运行入口,一般是程序启动的脚本和参数 层( Layer ) 在BaseImage基…...
【CFP-专栏2】计算机类SCI优质期刊汇总(含IEEE/Top)
一、计算机区块链类SCI-IEEE 【期刊概况】IF:4.0-5.0, JCR2区,中科院2区; 【大类学科】计算机科学; 【检索情况】SCI在检; 【录用周期】3-5个月左右录用; 【截稿时间】12.31截稿; 【接收领域】区块链…...

Stable Diffusion 本地部署详细教程
目录 一、前言二、系统和硬件要求三、安装前说明四、安装步骤5、升级pip(这是管理python环境软件工具),并把资源库换成国内地址为清华镜像。一、前言 虽然MJ和SD都可以生成图像,但是为什么我们要考虑使用本地SD部署呢?原因其实很简单:首先,本地部署的使用成本更低,且更加…...
【超图】SuperMap iClient3D for WebGL/WebGPU —— 坐标系位置 —— Cartesian2
作者:taco 说到关于地理必然逃不开位置的关系。借用百度百科的内容来说地理学(geography),是研究地球表层空间地理要素或者地理综合体空间分布规律、时间演变过程和区域特征的一门学科。所以位置&坐标系必然逃不掉了。那么在S…...
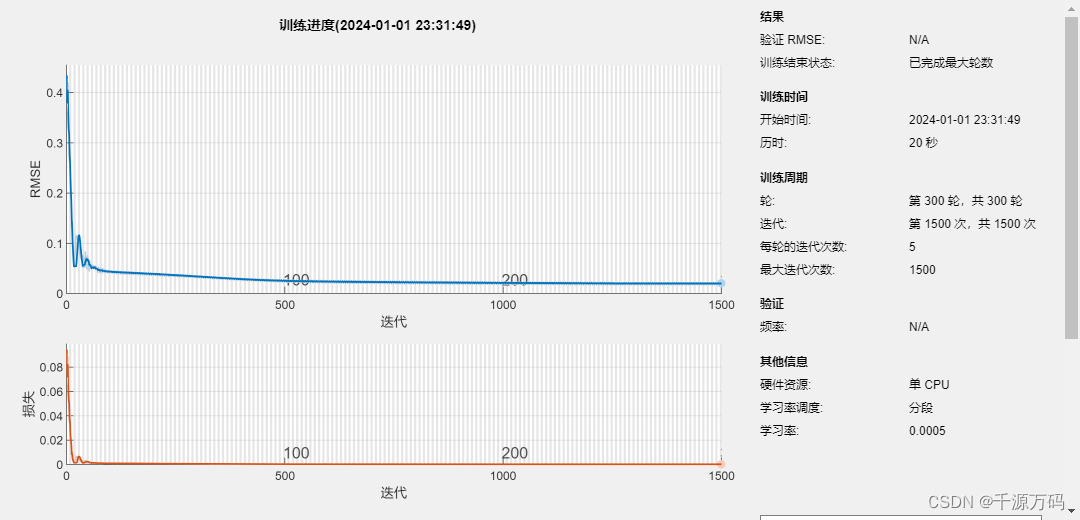
【Matlab】LSTM长短期记忆神经网络时序预测算法(附代码)
资源下载: https://download.csdn.net/download/vvoennvv/88688439 一,概述 LSTM(Long Short-Term Memory)是一种常用的循环神经网络(Recurrent Neural Network,RNN)结构,由于其对于…...

2.2 设计FMEA步骤二:结构分析
2.2.1 目的 设计结构分析的目的是将设计识别和分解为系统、子系统、组件和零件,以便进行技术风险分析。其主要目标包括: 可视化分析范围结构化表示:方块图、边界图、数字模型、实体零件识别设计接口、交互作用和间隙促进顾客和供应商工程团队之间的协作(接口责任)为功能分…...

红队攻防实战之DC2
吾愿效法古圣先贤,使成千上万的巧儿都能在21世纪的中华盛世里,丰衣足食,怡然自得 0x01 信息收集: 1.1 端口探测 使用nmap工具 可以发现开放了80端口,网页服务器但是可以看出做了域名解析,所以需要在本地完成本地域名…...

接口测试中缓存处理策略
在接口测试中,缓存处理策略是一个关键环节,直接影响测试结果的准确性和可靠性。合理的缓存处理策略能够确保测试环境的一致性,避免因缓存数据导致的测试偏差。以下是接口测试中常见的缓存处理策略及其详细说明: 一、缓存处理的核…...

Objective-C常用命名规范总结
【OC】常用命名规范总结 文章目录 【OC】常用命名规范总结1.类名(Class Name)2.协议名(Protocol Name)3.方法名(Method Name)4.属性名(Property Name)5.局部变量/实例变量(Local / Instance Variables&…...
【机器视觉】单目测距——运动结构恢复
ps:图是随便找的,为了凑个封面 前言 在前面对光流法进行进一步改进,希望将2D光流推广至3D场景流时,发现2D转3D过程中存在尺度歧义问题,需要补全摄像头拍摄图像中缺失的深度信息,否则解空间不收敛…...

Nuxt.js 中的路由配置详解
Nuxt.js 通过其内置的路由系统简化了应用的路由配置,使得开发者可以轻松地管理页面导航和 URL 结构。路由配置主要涉及页面组件的组织、动态路由的设置以及路由元信息的配置。 自动路由生成 Nuxt.js 会根据 pages 目录下的文件结构自动生成路由配置。每个文件都会对…...

生成 Git SSH 证书
🔑 1. 生成 SSH 密钥对 在终端(Windows 使用 Git Bash,Mac/Linux 使用 Terminal)执行命令: ssh-keygen -t rsa -b 4096 -C "your_emailexample.com" 参数说明: -t rsa&#x…...

Module Federation 和 Native Federation 的比较
前言 Module Federation 是 Webpack 5 引入的微前端架构方案,允许不同独立构建的应用在运行时动态共享模块。 Native Federation 是 Angular 官方基于 Module Federation 理念实现的专为 Angular 优化的微前端方案。 概念解析 Module Federation (模块联邦) Modul…...

微信小程序云开发平台MySQL的连接方式
注:微信小程序云开发平台指的是腾讯云开发 先给结论:微信小程序云开发平台的MySQL,无法通过获取数据库连接信息的方式进行连接,连接只能通过云开发的SDK连接,具体要参考官方文档: 为什么? 因为…...

优选算法第十二讲:队列 + 宽搜 优先级队列
优选算法第十二讲:队列 宽搜 && 优先级队列 1.N叉树的层序遍历2.二叉树的锯齿型层序遍历3.二叉树最大宽度4.在每个树行中找最大值5.优先级队列 -- 最后一块石头的重量6.数据流中的第K大元素7.前K个高频单词8.数据流的中位数 1.N叉树的层序遍历 2.二叉树的锯…...

听写流程自动化实践,轻量级教育辅助
随着智能教育工具的发展,越来越多的传统学习方式正在被数字化、自动化所优化。听写作为语文、英语等学科中重要的基础训练形式,也迎来了更高效的解决方案。 这是一款轻量但功能强大的听写辅助工具。它是基于本地词库与可选在线语音引擎构建,…...
Reasoning over Uncertain Text by Generative Large Language Models
https://ojs.aaai.org/index.php/AAAI/article/view/34674/36829https://ojs.aaai.org/index.php/AAAI/article/view/34674/36829 1. 概述 文本中的不确定性在许多语境中传达,从日常对话到特定领域的文档(例如医学文档)(Heritage 2013;Landmark、Gulbrandsen 和 Svenevei…...
