LeetCode题目笔记——1487. 保证文件名唯一
文章目录
- 题目描述
- 题目链接
- 题目难度——中等
- 方法一:哈希表
- 代码/Python
- 代码/C++
- 总结
题目描述
给你一个长度为 n 的字符串数组 names 。你将会在文件系统中创建 n 个文件夹:在第 i 分钟,新建名为 names[i] 的文件夹。
由于两个文件 不能 共享相同的文件名,因此如果新建文件夹使用的文件名已经被占用,系统会以 (k) 的形式为新文件夹的文件名添加后缀,其中 k 是能保证文件名唯一的 最小正整数 。
返回长度为 n 的字符串数组,其中 ans[i] 是创建第 i 个文件夹时系统分配给该文件夹的实际名称。
示例 1:
输入:names = ["pes","fifa","gta","pes(2019)"]
输出:["pes","fifa","gta","pes(2019)"]
解释:文件系统将会这样创建文件名:
"pes" --> 之前未分配,仍为 "pes"
"fifa" --> 之前未分配,仍为 "fifa"
"gta" --> 之前未分配,仍为 "gta"
"pes(2019)" --> 之前未分配,仍为 "pes(2019)"
示例 2:
输入:names = ["gta","gta(1)","gta","avalon"]
输出:["gta","gta(1)","gta(2)","avalon"]
解释:文件系统将会这样创建文件名:
"gta" --> 之前未分配,仍为 "gta"
"gta(1)" --> 之前未分配,仍为 "gta(1)"
"gta" --> 文件名被占用,系统为该名称添加后缀 (k),由于 "gta(1)" 也被占用,所以 k = 2 。实际创建的文件名为 "gta(2)" 。
"avalon" --> 之前未分配,仍为 "avalon"
示例 3:
输入:names = ["onepiece","onepiece(1)","onepiece(2)","onepiece(3)","onepiece"]
输出:["onepiece","onepiece(1)","onepiece(2)","onepiece(3)","onepiece(4)"]
解释:当创建最后一个文件夹时,最小的正有效 k 为 4 ,文件名变为 "onepiece(4)"。
示例 4:
输入:names = ["wano","wano","wano","wano"]
输出:["wano","wano(1)","wano(2)","wano(3)"]
解释:每次创建文件夹 "wano" 时,只需增加后缀中 k 的值即可。
示例 5:
输入:names = ["kaido","kaido(1)","kaido","kaido(1)"]
输出:["kaido","kaido(1)","kaido(2)","kaido(1)(1)"]
解释:注意,如果含后缀文件名被占用,那么系统也会按规则在名称后添加新的后缀 (k) 。
提示:
- 1 <= names.length <= 5 * 10^4
- 1 <= names[i].length <= 20
- names[i] 由小写英文字母、数字和/或圆括号组成。
题目链接
题目难度——中等
方法一:哈希表
我们需要一个哈希表seen来记录每个文件名的出现次数,同时以这个出现次数作为我们获取答案的依据之一。
代码/Python
class Solution:def getFolderNames(self, names):used_names = {}result = []for name in names:if name not in used_names:# 如果名称没有被占用,直接使用used_names[name] = 1result.append(name)else:# 如果名称被占用,就把出现次数++k = used_names[name]while f"{name}({k})" in used_names:k += 1used_names[f"{name}({k})"] = 1result.append(f"{name}({k})")used_names[name] = k + 1 # 下一次要判断的return result
代码/C++
class Solution {
public:vector<string> getFolderNames(vector<string>& names) {map<string, int> seen;vector<string> res;for(auto name: names){// seen.count返回出现次数,find返回指向元素的迭代器if(!seen.count(name)){res.push_back(name);seen[name] = 1;}else{int k = seen[name];while(seen.count(name + "(" + to_string(k) + ")")){k++;}string t = name + "(" + to_string(k) + ")";seen[t] = 1;res.push_back(t);seen[name] = k + 1;}}return res;}
};
上面的代码还可以写得更简单一些,直接用一个while来代替if-else,以python为例:
class Solution:def getFolderNames(self, names):seen = dict()res = []for name in names:n = namewhile n in seen:n = f'{name}({seen[name]})'seen[name] += 1seen[n] = 1res.append(n)return res
总结
方法一时间复杂度应该是O(N)级的,空间复杂度O(N)。
相关文章:

LeetCode题目笔记——1487. 保证文件名唯一
文章目录题目描述题目链接题目难度——中等方法一:哈希表代码/Python代码/C总结题目描述 给你一个长度为 n 的字符串数组 names 。你将会在文件系统中创建 n 个文件夹:在第 i 分钟,新建名为 names[i] 的文件夹。 由于两个文件 不能 共享相同…...
【概念辨析】结构体内存对齐
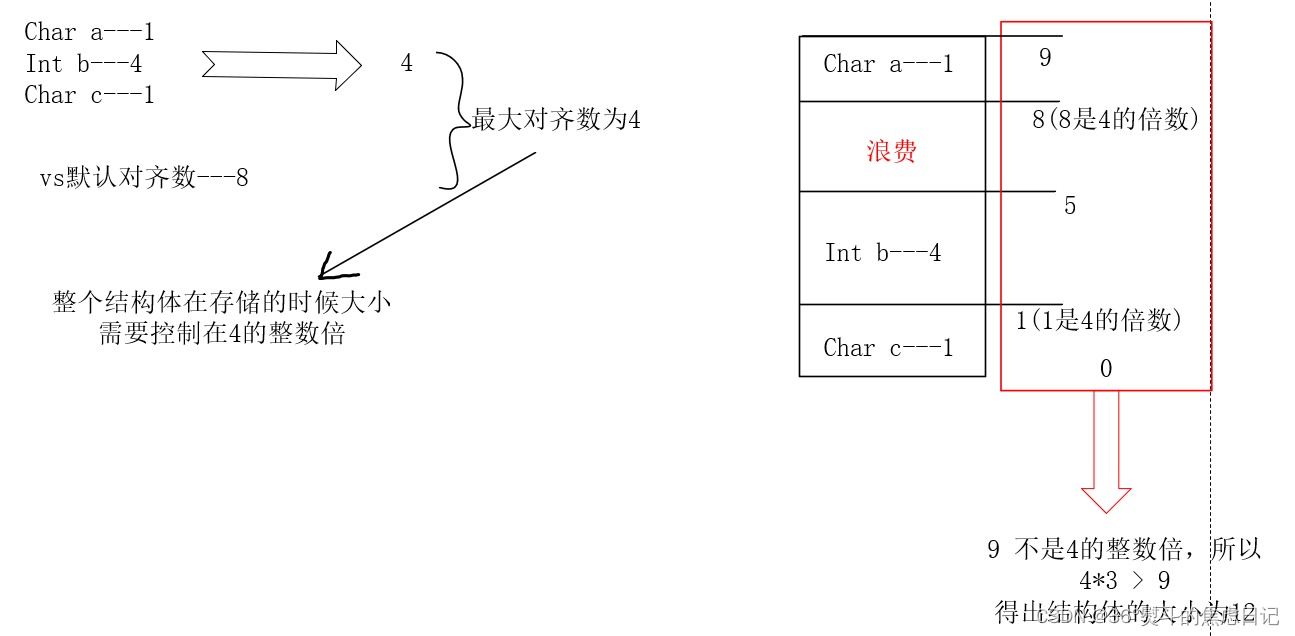
一、什么是结构体内存对齐 是使得结构体的每个成员能够在及其访问的特定存储单元上的一种方法。 通过这种方法可以使得机器访问效率加快,也可以使得平台一致性变高。 二、结构体对齐的规则 有两组代码: #define _CRT_SECURE_NO_WARNINGS#include <…...
pg mysql oracle 中的schema
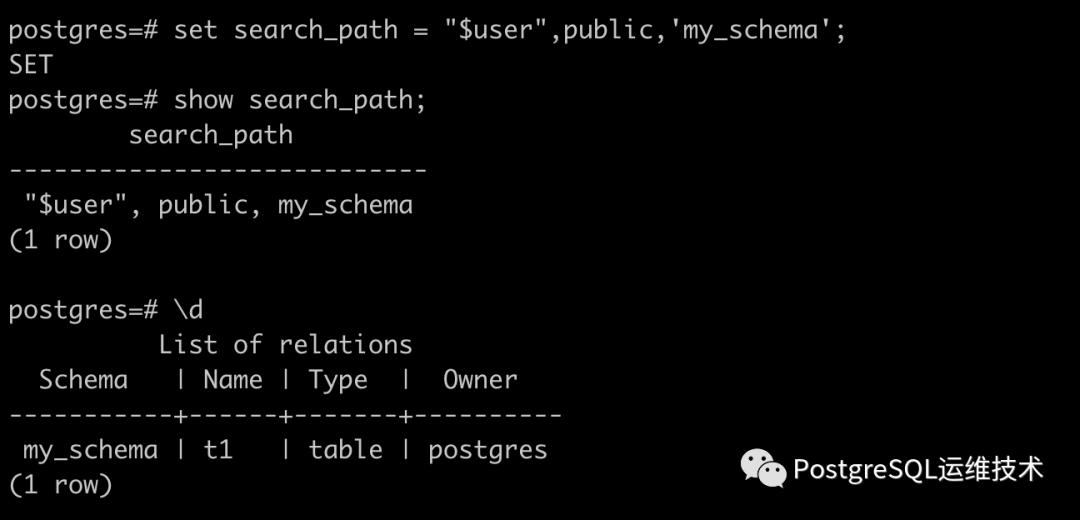
1、schema。 pg中的schema表示当前db中数据库对象的命名空间(namespace),数据库对象包括但不限于表、函数、视图、索引等。 对于熟悉mysql的人来说,在第一次看到pg中的schema的概念时,可能会疑惑,schema不是表示database的吗&…...
电脑快捷方式删除文件后四种找回方法
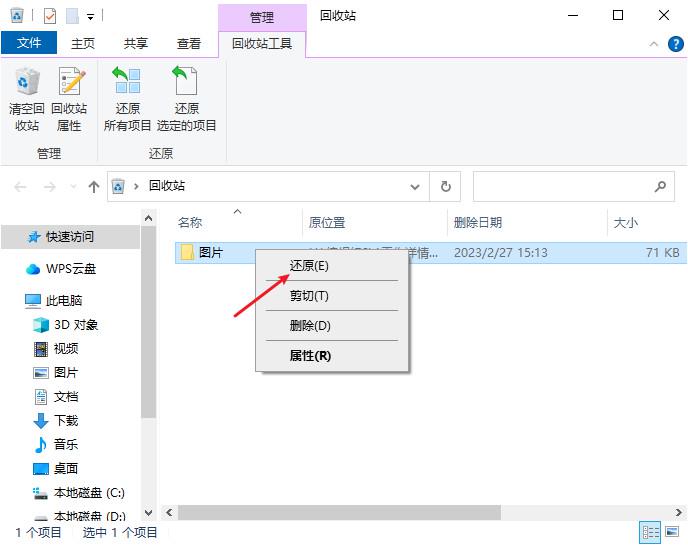
快捷指令是一种用作替代快捷键操作的技术。也可以称为“快捷键”,“快捷方式”或“快捷键序列”,它们允许用户在非常快速和方便的方式建立特定操作序列,这对于执行重复性或提高效率非常有用。通过使用快捷指令,您可以执行快速复制…...
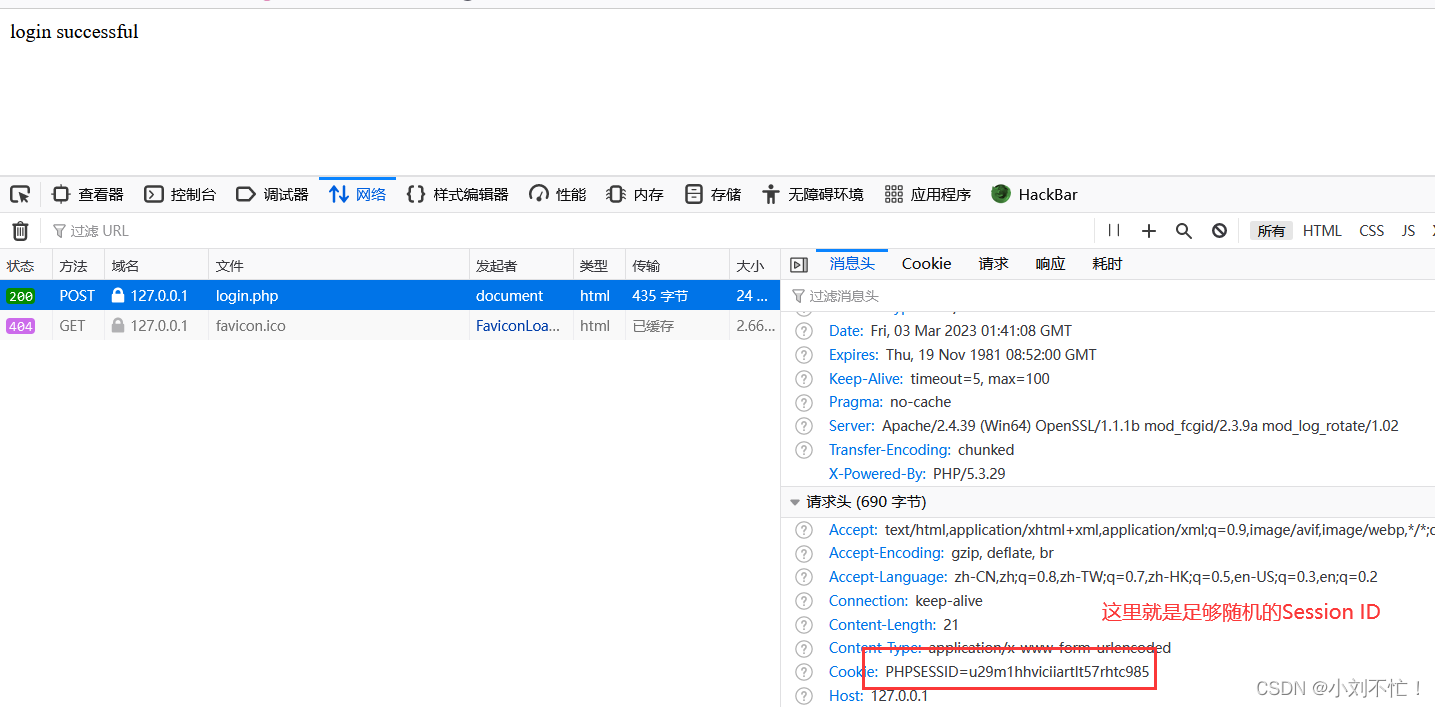
Session会话管理
会话管理Web会话管理概述常见的Web应用会话管理方式基于Server端的Session的管理方式基于Cookie的Session的管理方式Cookie与Session最大的区别Cookie-Based的管理方式基于Token-Based的管理方式Web会话管理的安全问题Web会话管理概述 会话管理:在进行人机交互的时…...

极智开发 | ubuntu源码编译cuda版opencv
欢迎关注我的公众号 [极智视界],获取我的更多经验分享 大家好,我是极智视界,本文介绍一下 ubuntu源码编译cuda版opencv。 邀您加入我的知识星球「极智视界」,星球内有超多好玩的项目实战源码下载,链接:https://t.zsxq.com/0aiNxERDq 如果你需要源码编译cpu版的opencv可以…...
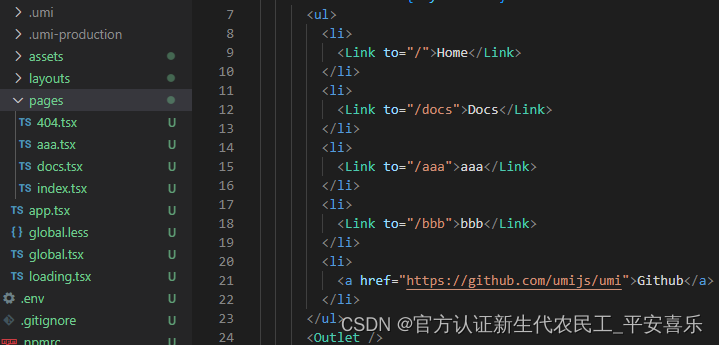
umi学习(umi4)
umi 官方文档 官方建议使用 pnpm node版本在 14 以上 创建项目: 根据 包管理工具不同 ,官方推荐 这里使用 pnpm: 1. pnpm dlx create-umilatest 2. 选择模板 (这里使用 Simple App) 想对module处理需要使用 Ant Desig…...

EasyPoi的excel模板预览与下载、导出简单/复杂数据
官方文档地址:easypoi官网,官方仅供参考,部分描述有问题 excel模板预览 准备工作 事先将整理好的excel模板存在项目中,如图 excel模板预览代码 GetMapping("excel")ApiOperation("excel预览")NoLogpubli…...

收个滴滴Offer:从小伙三面经历,看看需要学点啥?
说在前面 在尼恩的(50)读者社群中,经常有小伙伴,需要面试大厂。 后续结合一些大厂的面试真题,给大家梳理一下学习路径,看看大家需要学点啥? 这里也一并把题目以及参考答案,收入咱…...
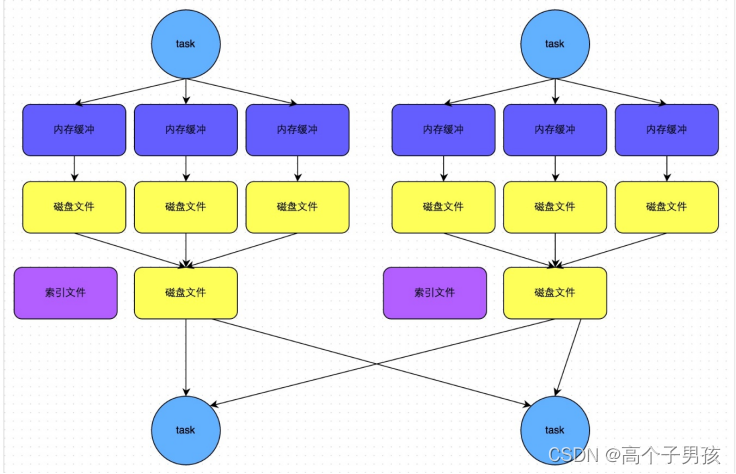
Spark Shuffle解析
1 Shuffle的核心要点 1.1 ShuffleMapStage与ResultStage ShuffleMapStage与ResultStage 在划分stage时,最后一个stage称为finalStage,它本质上是一个ResultStage对象,前面的所有stage被称为ShuffleMapStage。 ShuffleMapStage的结束伴随着…...

Qt 解决程序全屏运行弹窗引发任务栏显示
文章目录摘要在VM虚拟机器中测试setWindowFlags()关键字: Qt、 Qt::WindowStayOnTopHint、 setWindowFlags、 Qt::Window、 Qt::Tool摘要 今天眼看项目就要交付了,结果在测试程序的时候,发现在程序全品情况下,点击输入框&#x…...
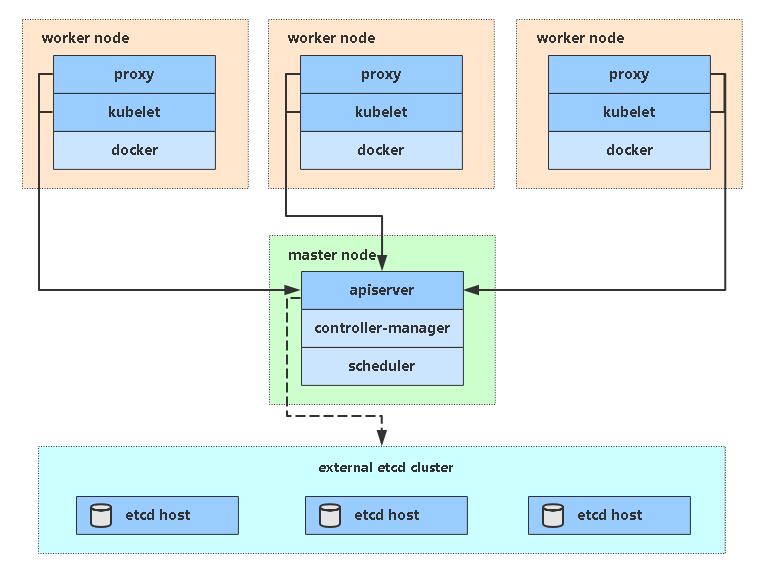
【进阶】2、搭建K8s集群【v1.23】
[toc] 一、安装要求 在开始之前,部署Kubernetes集群机器需要满足以下几个条件: 一台或多台机器,操作系统 CentOS7.x-86_x64硬件配置:2GB或更多RAM,2个CPU或更多CPU,硬盘30GB或更多集群中所有机器之间网络…...
:一切皆服务,服务基于协议)
11面向接口编程(下):一切皆服务,服务基于协议
服务容器的实现 一个服务容器主要的功能是:为服务提供注册绑定、提供获取服务实例,所以服务容器至少有两个方法:注册方法 Bind、获取实例方法 Make。 对于注册的方法,直接将一个服务提供者注册到容器中,参数是之前定…...
不要以没时间来说测试用例写不好
工作当中,总会有人为自己的测试用例写得不够好去找各种理由,时间不够是我印象当中涉及到最多的,也是最反感。想写好测试用例,前提是测试分析和需求拆解做的足够好,通过xmind或者UML图把需求和开发设计提供的产品信息提炼出来。 我个人的提炼标准一般是&…...

day57-day58【代码随想录】二刷数组
文章目录前言一、螺旋矩阵||(力扣59)二、螺旋矩阵(力扣54)三、顺时针打印矩阵(剑指 Offer29)四、在排序数组中查找元素的第一个和最后一个位置(力扣34)【二分查找】五、有多少小于当…...
【NLP】自动化计算文本文件TTR的bash脚本
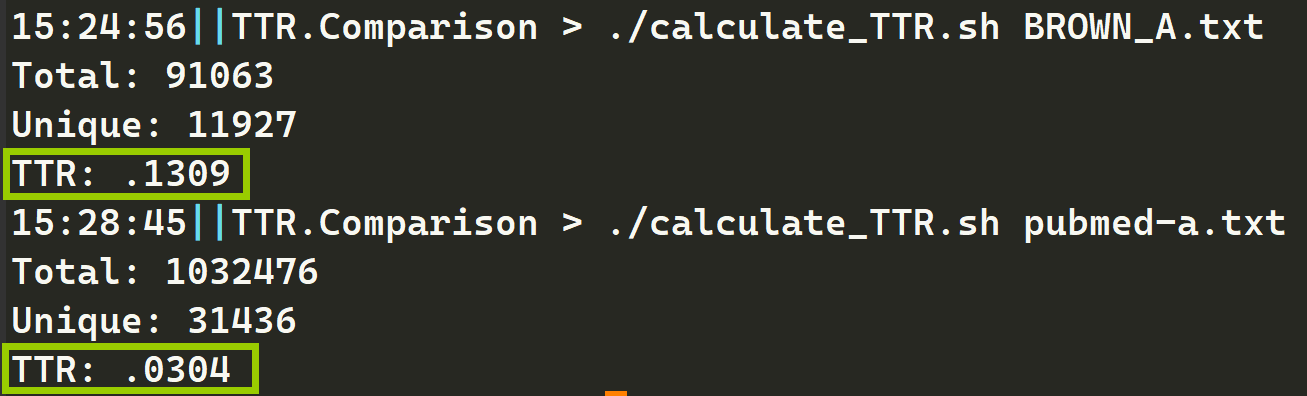
自动化计算文本文件TTR的bash脚本 简介 这是一个可以计算文本文件TTR的bash脚本,文件名为:calculate_TTR.sh。它会接收一个文件名作为参数,并输出总单词数、特异单词数和TTR。 TTR是什么 TTR(Type-Token Ratio)是用…...

蓝桥杯单片机组省赛十二届第一场(关于矩阵,温度ds18b20,时间ds1302的学习,以及继电器等外设的综合利用)
提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档 文章目录一、该题目如下二、使用步骤1.矩阵键盘实现2.温度传感器ds18b20的实现总结提示:以下是本篇文章正文内容,下面案例可供参考 一、该题目如下 分…...
Ubuntu 新人上手 Microk8s 指南
文章目录1. 什么是 Ubuntu 核心2. 什么是 Kubernetes3. 什么是MicroK8s4. 为什么选择 Microk8s on Core5. 安装Ubuntu Core6. Ubuntu Core上安装 MicroK8S7. 启动 Microk8s8. 启用必要的 MicroK8s 插件9. 部署示例容器工作负载10. 检查部署状态并访问您的应用程序11. 管理镜像1…...

初阶C语言——实用调试技巧【详解】
文章目录1. 什么是bug?2. 调试是什么?有多重要?2.1 调试是什么?2.2 调试的基本步骤2.3 Debug和Release的介绍3.学会使用快捷键4.调试的时候查看程序当前信息4.1 查看临时变量的值4.2 查看内存信息4.3 查看调用堆栈4.4 查看汇编信息…...
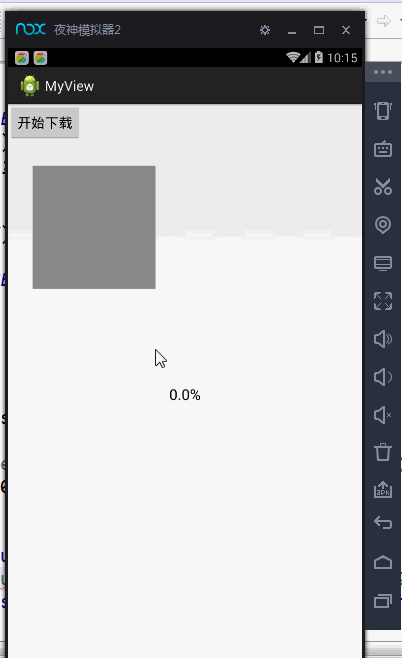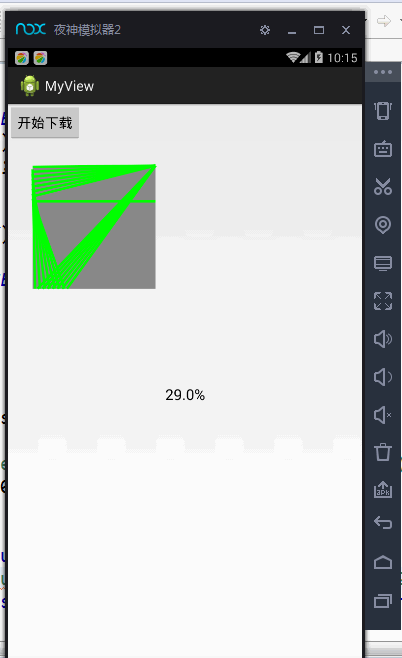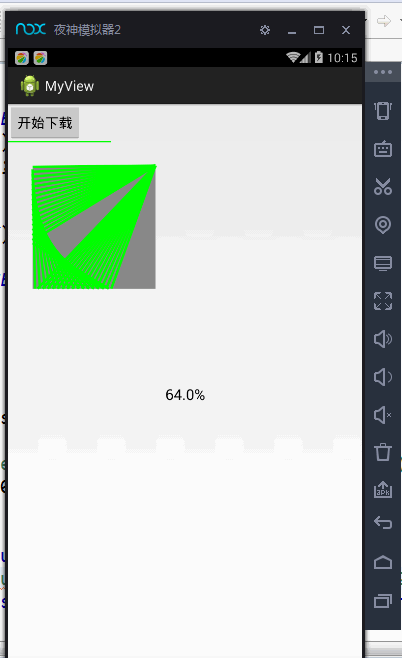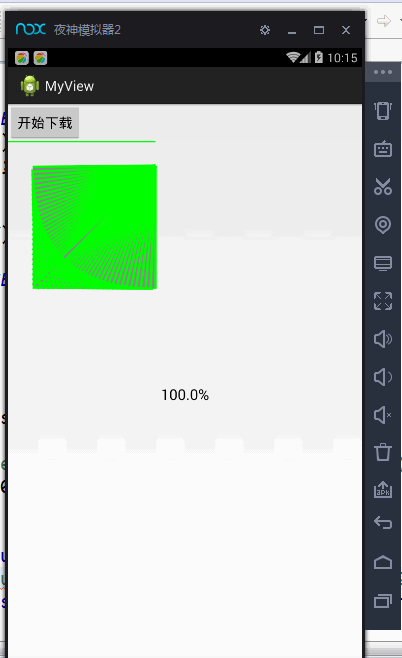
Android 绘图基础:Canvas画布——自定义View基础(绘制表盘、矩形、圆形、弧、渐变)
Canvas画布,通过它我们可以自定义一个View,设置View的相关效果之类的。感觉用法差不多,重要的是要理解方法中传入的参数的含义,比如float类型的参数,传递的是坐标,已开是没有注意传入的参数时坐标,导致我迷…...

【Python】 -- 趣味代码 - 小恐龙游戏
文章目录 文章目录 00 小恐龙游戏程序设计框架代码结构和功能游戏流程总结01 小恐龙游戏程序设计02 百度网盘地址00 小恐龙游戏程序设计框架 这段代码是一个基于 Pygame 的简易跑酷游戏的完整实现,玩家控制一个角色(龙)躲避障碍物(仙人掌和乌鸦)。以下是代码的详细介绍:…...
-----深度优先搜索(DFS)实现)
c++ 面试题(1)-----深度优先搜索(DFS)实现
操作系统:ubuntu22.04 IDE:Visual Studio Code 编程语言:C11 题目描述 地上有一个 m 行 n 列的方格,从坐标 [0,0] 起始。一个机器人可以从某一格移动到上下左右四个格子,但不能进入行坐标和列坐标的数位之和大于 k 的格子。 例…...

Android Bitmap治理全解析:从加载优化到泄漏防控的全生命周期管理
引言 Bitmap(位图)是Android应用内存占用的“头号杀手”。一张1080P(1920x1080)的图片以ARGB_8888格式加载时,内存占用高达8MB(192010804字节)。据统计,超过60%的应用OOM崩溃与Bitm…...

管理学院权限管理系统开发总结
文章目录 🎓 管理学院权限管理系统开发总结 - 现代化Web应用实践之路📝 项目概述🏗️ 技术架构设计后端技术栈前端技术栈 💡 核心功能特性1. 用户管理模块2. 权限管理系统3. 统计报表功能4. 用户体验优化 🗄️ 数据库设…...

基于Java Swing的电子通讯录设计与实现:附系统托盘功能代码详解
JAVASQL电子通讯录带系统托盘 一、系统概述 本电子通讯录系统采用Java Swing开发桌面应用,结合SQLite数据库实现联系人管理功能,并集成系统托盘功能提升用户体验。系统支持联系人的增删改查、分组管理、搜索过滤等功能,同时可以最小化到系统…...

安宝特方案丨船舶智造的“AR+AI+作业标准化管理解决方案”(装配)
船舶制造装配管理现状:装配工作依赖人工经验,装配工人凭借长期实践积累的操作技巧完成零部件组装。企业通常制定了装配作业指导书,但在实际执行中,工人对指导书的理解和遵循程度参差不齐。 船舶装配过程中的挑战与需求 挑战 (1…...

MinIO Docker 部署:仅开放一个端口
MinIO Docker 部署:仅开放一个端口 在实际的服务器部署中,出于安全和管理的考虑,我们可能只能开放一个端口。MinIO 是一个高性能的对象存储服务,支持 Docker 部署,但默认情况下它需要两个端口:一个是 API 端口(用于存储和访问数据),另一个是控制台端口(用于管理界面…...

MyBatis中关于缓存的理解
MyBatis缓存 MyBatis系统当中默认定义两级缓存:一级缓存、二级缓存 默认情况下,只有一级缓存开启(sqlSession级别的缓存)二级缓存需要手动开启配置,需要局域namespace级别的缓存 一级缓存(本地缓存&#…...

Monorepo架构: Nx Cloud 扩展能力与缓存加速
借助 Nx Cloud 实现项目协同与加速构建 1 ) 缓存工作原理分析 在了解了本地缓存和远程缓存之后,我们来探究缓存是如何工作的。以计算文件的哈希串为例,若后续运行任务时文件哈希串未变,系统会直接使用对应的输出和制品文件。 2 …...

车载诊断架构 --- ZEVonUDS(J1979-3)简介第一篇
我是穿拖鞋的汉子,魔都中坚持长期主义的汽车电子工程师。 老规矩,分享一段喜欢的文字,避免自己成为高知识低文化的工程师: 做到欲望极简,了解自己的真实欲望,不受外在潮流的影响,不盲从,不跟风。把自己的精力全部用在自己。一是去掉多余,凡事找规律,基础是诚信;二是…...
