Java异常篇----第二篇
相关文章:

Java异常篇----第二篇
系列文章目录 文章目录 系列文章目录前言一、 Excption与Error包结构二、Thow与thorws区别三、Error与Exception区别?四、error和exception有什么区别前言 前些天发现了一个巨牛的人工智能学习网站,通俗易懂,风趣幽默,忍不住分享一下给大家。点击跳转到网站,这篇文章男女…...
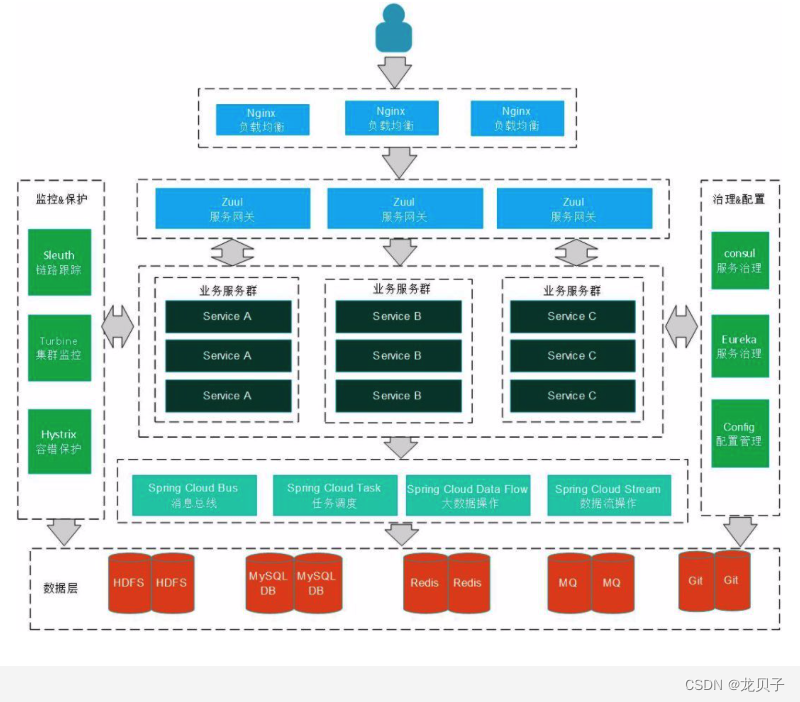
微服务(1)
目录 1.什么是微服务?谈谈你对微服务的理解? 2.什么是Spring Cloud? 3.Springcloud中的组件有哪些? 3.具体说说SpringCloud主要项目? 5.SpringCloud项目部署架构? 1.什么是微服务?谈谈你对微…...
】5G 网络建设(最小生成树—JavaPythonC++JS实现))
195.【2023年华为OD机试真题(C卷)】5G 网络建设(最小生成树—JavaPythonC++JS实现)
请到本专栏顶置查阅最新的华为OD机试宝典 点击跳转到本专栏-算法之翼:华为OD机试 🚀你的旅程将在这里启航!本专栏所有题目均包含优质解题思路,高质量解题代码,详细代码讲解,助你深入学习,深度掌握! 文章目录 【2023年华为OD机试真题(C卷)】5G 网络建设(最小生…...

2024年1月1日答案
a)i. V B B V C C 16 V V_{BB} V_{CC} 16V VBBVCC16V R t h R B R E R B R E 10 k Ω 3 k Ω 10 k Ω 3 k Ω ≈ 2.31 k Ω R_{th} \frac{R_B \times R_E}{R_B R_E} \frac{10k\Omega \times 3k\Omega}{10k\Omega 3k\Omega} \approx 2.31k\Omega RthRBR…...

【算法】dp题单
题单链接: https://vjudge.net/contest/574209#overview 目录 1. 洛谷 P1020 导弹拦截 (dp二分Dilworth 定理) 2. P1439 最长公共子序列(二分求最长公共子序列) 3. 洛谷 P1854 花店橱窗布置 (线性dp 用…...
)
Verilog视频信号图形显示 FPGA(iCE40)
您需要一块带视频输出的 FPGA 板。 我们将在 640x480 下工作,几乎任何视频输出都可以在此像素工作。 它有助于轻松地对 FPGA 板进行编程并相当熟悉 Verilog。 如果您没有开发板,请不要担心,您可以使用 Verilator 模拟器。 材料 Lattice iCE…...

【LeetCode 面试经典150题】26. Remove Duplicates from Sorted Array 在有序数组中移除重复元素
26. Remove Duplicates from Sorted Array 题目大意 Given an integer array nums sorted in non-decreasing order, remove the duplicates in-place such that each unique element appears only once. The relative order of the elements should be kept the same. Then …...

linux系统下sql脚本的执行与导出
terminal中执行 执行 mysql -u [username] -p -D [databasename] < [XXX.sql] 导出 mysql -u [username] -p [datbasename] > [XXX.sql] 导出的数据库名自定义。 mysql -u [username] -p [databasename] [tablename] > [xxx.sql] 导出表名自定义 mysql shell 执行 …...
MyBatis学习一:快速入门
前言 公司要求没办法,前端也要了解一下后端知识,这里记录一下自己的学习 学习教程:黑马mybatis教程全套视频教程,2天Mybatis框架从入门到精通 文档: https://mybatis.net.cn/index.html MyBatis 快速入门…...

零售业物流这个防漏水技术,居然没有翻车!
随着科技的不断发展,水浸监控系统在各个领域得到了广泛应用。水浸监控不仅仅是为了保护建筑结构和设备,更是为了防范因水灾引起的生命安全和财产损失。 因此,为了有效预防和应对水浸事件,水浸监控系统应运而生,成为各行…...

主浏览器优化之路1——你现在在用的是什么浏览器?Edge?谷歌?火狐?360!?
上一世,我的浏览器之路 引言为什么要用两个浏览器为什么一定要放弃火狐结尾给大家一个猜数字小游戏(测运气) 引言 小时候,我一开始上网的浏览器是2345王牌浏览器吧, 因为上面集成了很多网站,我记得上面有7…...

gitlab请求合并分支
直接去看原文: 原文链接:Gitlab合并请求相关流程_source branch target branch-CSDN博客 --------------------------------------------------------------------------------------------------------------------------------- 入口: 仓库控制台的这两个地方都…...
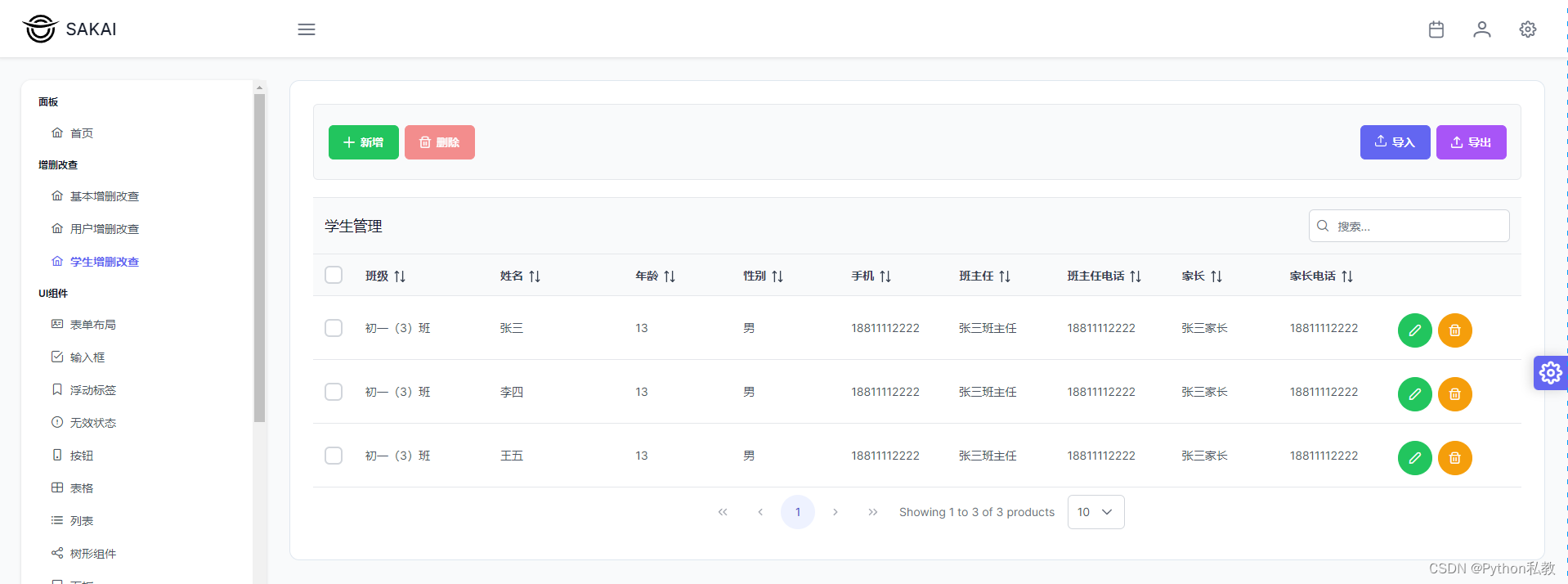
使用Vue3开发学生管理系统模板1
环境搭建 通过解压之前《Vue3开发后台管理系统模板》的代码,我们能够得到用户增删改查的页面,我们基于用户增删改查的页面做进一步的优化。 创建学生增删改查页面 第一步:复制用户增删改查页面,重命名为StudentCRUD.vue <…...
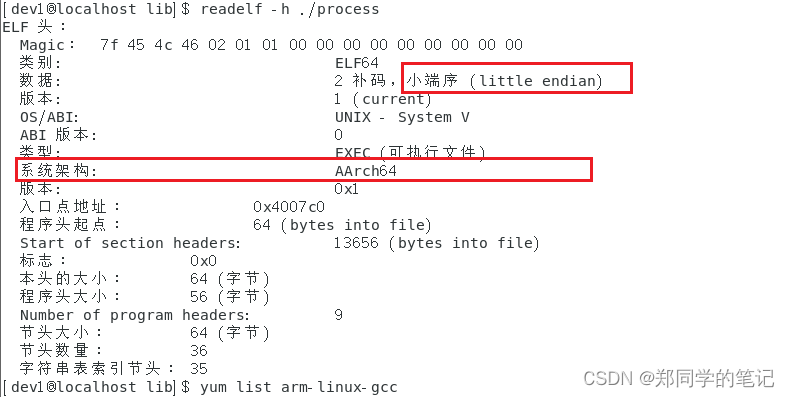
【cmake实战:番外】交叉编译——Linaro
【cmake实战:番外】交叉编译——Linaro 一、交叉编译1、交叉编译简介2、为什么会有交叉编译 二、交叉编译链1、什么是交叉编译链2、交叉编译工具 三、Linaro1、下载2、解压3、demo3.1、toolchain_aarch64.cmake3.2、CMakeLists.txt3.3、main.cpp 4、执行编译5、查看…...
)
2024年年初Java5年实战面试题(北京)
高阶篇: 一、在面对千万条并发请求的情况下,如果数据库频繁查询导致崩溃,可以采取以下措施来解决问题: 1.缓存数据:可以使用缓存技术来减少对数据库的查询次数。将经常查询的数据存储在缓存中,例如使用Redis等内存数据库ÿ…...
【Apache-2.0】springboot-openai-chatgpt超级AI大脑产品架构图
springboot-openai-chatgpt: 一个基于SpringCloud的Chatgpt机器人,已对接GPT-3.5、GPT-4.0、百度文心一言、stable diffusion AI绘图、Midjourney绘图。用户可以在界面上与聊天机器人进行对话,聊天机器人会根据用户的输入自动生成回复。同时也支持画图&a…...

如何在iPhone设备中查看崩溃日志
目录 如何在iPhone设备中查看崩溃日志 摘要 引言 导致iPhone设备崩溃的主要原因是什么? 使用克魔助手查看iPhone设备中的崩溃日志 奔溃日志分析 总结 摘要 本文介绍了如何在iPhone设备中查看崩溃日志,以便调查崩溃的原因。我们将展示三种不同的…...

对接第三方接口鉴权(Spring Boot+Aop+注解实现Api接口签名验证)
前言 一个web系统,从接口的使用范围也可以分为对内和对外两种,对内的接口主要限于一些我们内部系统的调用,多是通过内网进行调用,往往不用考虑太复杂的鉴权操作。但是,对于对外的接口,我们就不得不重视这个…...
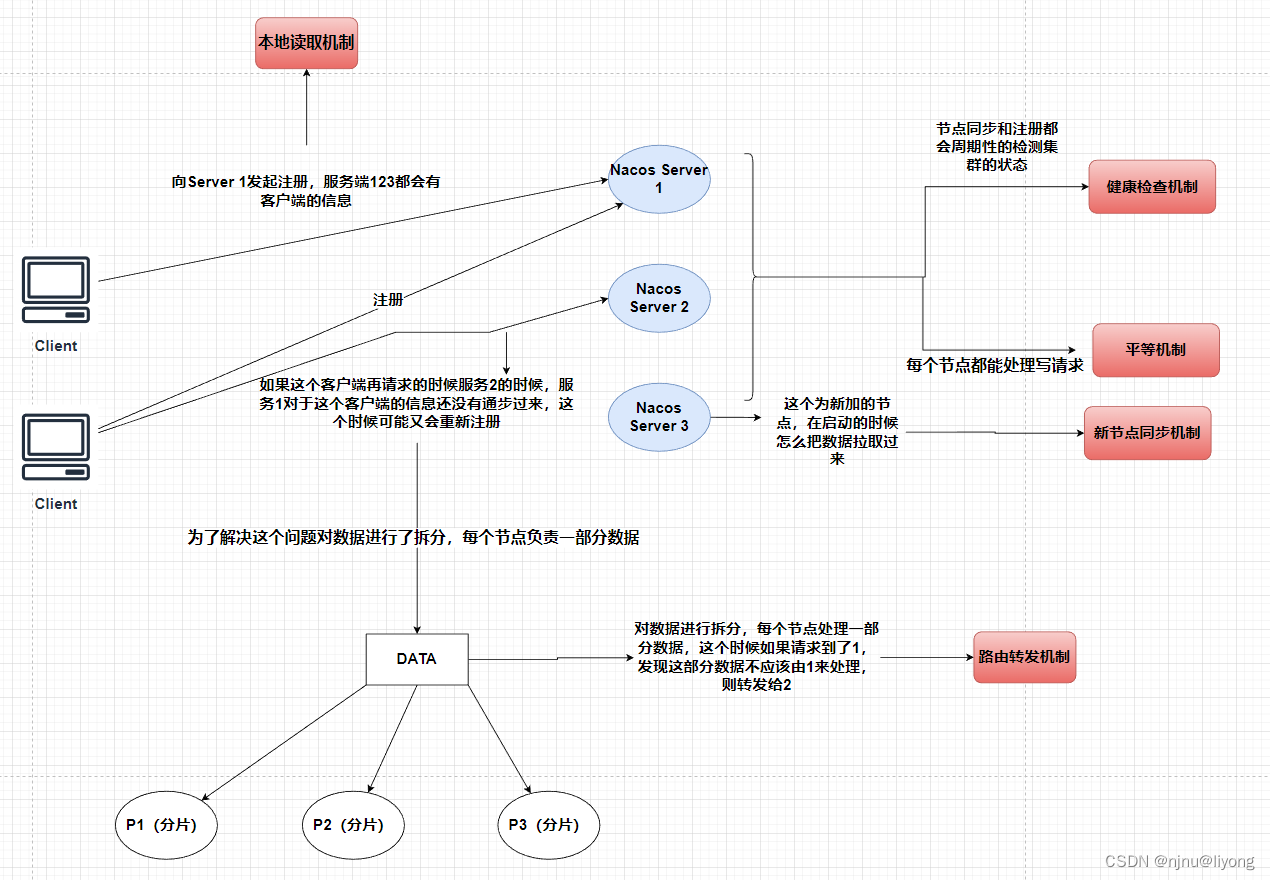
微服务-理论(CAP,一致性协议)
CAP理论 关于CAP理论的介绍可以直接看这篇文章 CAP分别是什么? 一致性(Consistency 一致性包括强一致性,弱一致性,最终一致性。 一致性其实是指数据的一致性,为什么数据会不一致呢? 如上面这张图&…...
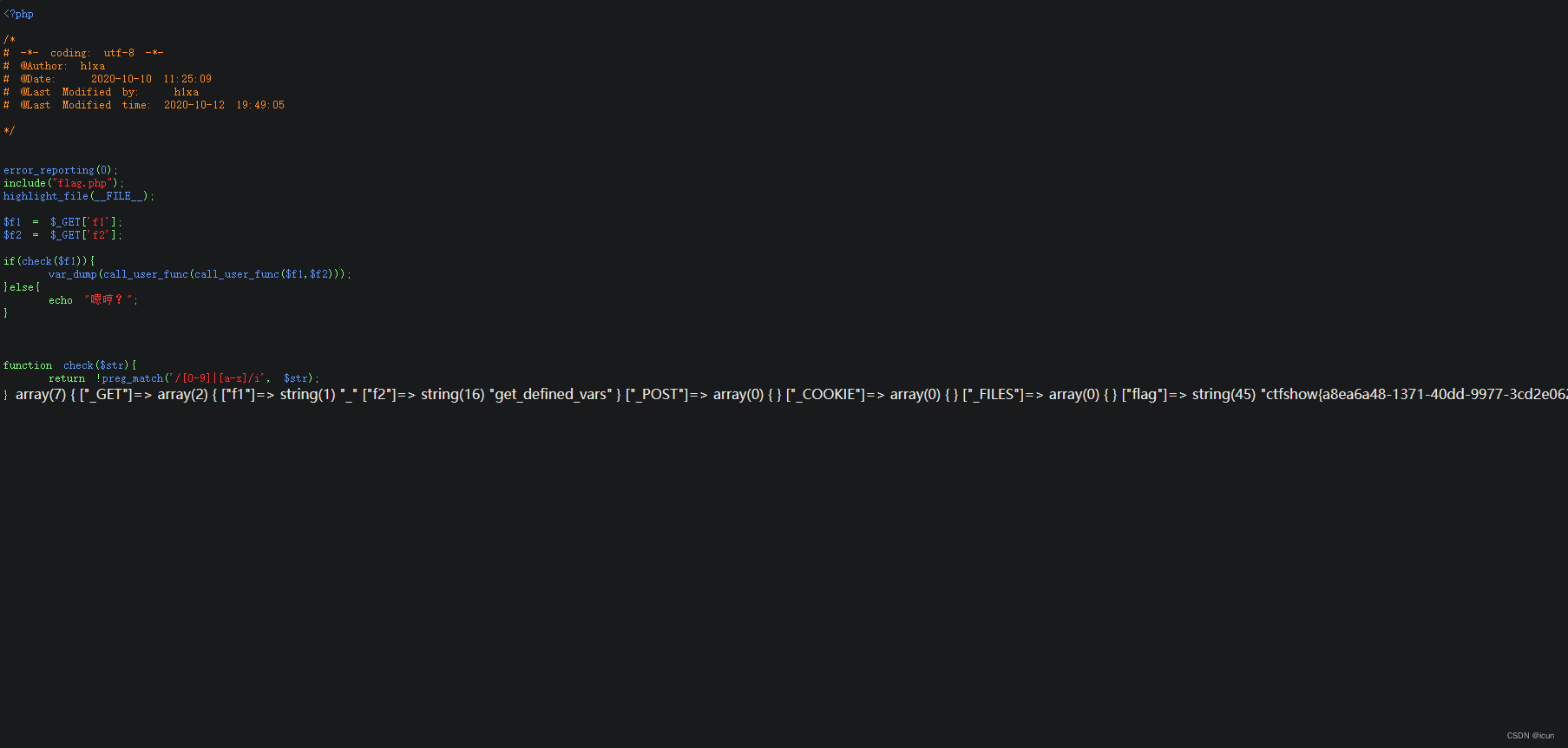
CTFshow web入门web128-php特性31
开启环境: 一个新的姿势,当php扩展目录下有php_gettext.dll时: _()是一个函数。 _()gettext() 是gettext()的拓展函数,开启text扩展get_defined_vars — 返回由所有已定义变量所组成的数组。 call_user_func — 把第一个参数作为回调函数调…...

挑战杯推荐项目
“人工智能”创意赛 - 智能艺术创作助手:借助大模型技术,开发能根据用户输入的主题、风格等要求,生成绘画、音乐、文学作品等多种形式艺术创作灵感或初稿的应用,帮助艺术家和创意爱好者激发创意、提高创作效率。 - 个性化梦境…...

vscode里如何用git
打开vs终端执行如下: 1 初始化 Git 仓库(如果尚未初始化) git init 2 添加文件到 Git 仓库 git add . 3 使用 git commit 命令来提交你的更改。确保在提交时加上一个有用的消息。 git commit -m "备注信息" 4 …...

剑指offer20_链表中环的入口节点
链表中环的入口节点 给定一个链表,若其中包含环,则输出环的入口节点。 若其中不包含环,则输出null。 数据范围 节点 val 值取值范围 [ 1 , 1000 ] [1,1000] [1,1000]。 节点 val 值各不相同。 链表长度 [ 0 , 500 ] [0,500] [0,500]。 …...

【论文笔记】若干矿井粉尘检测算法概述
总的来说,传统机器学习、传统机器学习与深度学习的结合、LSTM等算法所需要的数据集来源于矿井传感器测量的粉尘浓度,通过建立回归模型来预测未来矿井的粉尘浓度。传统机器学习算法性能易受数据中极端值的影响。YOLO等计算机视觉算法所需要的数据集来源于…...

MySQL 8.0 OCP 英文题库解析(十三)
Oracle 为庆祝 MySQL 30 周年,截止到 2025.07.31 之前。所有人均可以免费考取原价245美元的MySQL OCP 认证。 从今天开始,将英文题库免费公布出来,并进行解析,帮助大家在一个月之内轻松通过OCP认证。 本期公布试题111~120 试题1…...

今日学习:Spring线程池|并发修改异常|链路丢失|登录续期|VIP过期策略|数值类缓存
文章目录 优雅版线程池ThreadPoolTaskExecutor和ThreadPoolTaskExecutor的装饰器并发修改异常并发修改异常简介实现机制设计原因及意义 使用线程池造成的链路丢失问题线程池导致的链路丢失问题发生原因 常见解决方法更好的解决方法设计精妙之处 登录续期登录续期常见实现方式特…...

2023赣州旅游投资集团
单选题 1.“不登高山,不知天之高也;不临深溪,不知地之厚也。”这句话说明_____。 A、人的意识具有创造性 B、人的认识是独立于实践之外的 C、实践在认识过程中具有决定作用 D、人的一切知识都是从直接经验中获得的 参考答案: C 本题解…...

return this;返回的是谁
一个审批系统的示例来演示责任链模式的实现。假设公司需要处理不同金额的采购申请,不同级别的经理有不同的审批权限: // 抽象处理者:审批者 abstract class Approver {protected Approver successor; // 下一个处理者// 设置下一个处理者pub…...

人机融合智能 | “人智交互”跨学科新领域
本文系统地提出基于“以人为中心AI(HCAI)”理念的人-人工智能交互(人智交互)这一跨学科新领域及框架,定义人智交互领域的理念、基本理论和关键问题、方法、开发流程和参与团队等,阐述提出人智交互新领域的意义。然后,提出人智交互研究的三种新范式取向以及它们的意义。最后,总结…...

vulnyx Blogger writeup
信息收集 arp-scan nmap 获取userFlag 上web看看 一个默认的页面,gobuster扫一下目录 可以看到扫出的目录中得到了一个有价值的目录/wordpress,说明目标所使用的cms是wordpress,访问http://192.168.43.213/wordpress/然后查看源码能看到 这…...
