[Angular] 笔记 23:Renderer2 - ElementRef 的生产版本
chatgpt:
Renderer2 简介
在 Angular 中,Renderer2 是一个服务,用于处理 DOM 操作的抽象层。它提供了一种安全的方式来操作 DOM,同时与平台无关,有助于维护应用程序的跨浏览器兼容性和安全性。
Renderer2 的作用是在 Angular 组件中执行 DOM 操作,例如创建元素、设置属性、添加监听器、修改样式等。通过使用 Renderer2,开发者可以避免直接操作原始的 DOM 元素,而是通过 Angular 提供的抽象层来处理这些操作。
使用 Renderer2 的好处包括:
平台无关性: Renderer2 提供了与平台无关的 DOM 操作,这意味着你的应用程序可以在不同的平台上运行,并且不需要针对特定浏览器或环境进行修改。
安全性: 通过 Renderer2 执行 DOM 操作可以提高应用程序的安全性,因为它会遵循 Angular 的安全策略,并减少潜在的安全风险,比如 XSS 攻击。
可测试性: 使用 Renderer2 可以更轻松地编写单元测试,因为你可以模拟和验证 DOM 操作,而无需实际操作 DOM。
使用 Renderer2 的例子可能如下所示:
import { Component, Renderer2, ElementRef, OnInit } from '@angular/core';@Component({selector: 'app-example',template: '<div #myDiv>Some content</div>',
})
export class ExampleComponent implements OnInit {constructor(private renderer: Renderer2, private el: ElementRef) {}ngOnInit() {const divElement = this.el.nativeElement.querySelector('#myDiv');// 使用 Renderer2 设置元素的样式this.renderer.setStyle(divElement, 'color', 'red');}
}
在这个例子中,Renderer2 被注入到了 ExampleComponent 的构造函数中,并用于设置 #myDiv 元素的文字颜色。这样,通过 Renderer2 来操作 DOM,而不是直接操作原始的 DOM 元素,提供了更好的安全性和跨平台兼容性。
为什么不叫 Renderer 而是叫 Renderer2 呢?
在 Angular 中,Renderer2 取代了早期版本中的 Renderer 接口。原先的 Renderer 接口存在一些限制和性能问题,并且与新的 Web 标准和浏览器 API 不够契合。
当 Angular 团队重新设计和改进渲染器接口时,他们引入了 Renderer2。Renderer2 提供了更好的抽象,更好地与现代浏览器 API 对接,同时也改善了性能和安全性。为了明确表示这是一个新的、改进过的版本,他们将其命名为 Renderer2,以示区别。
虽然 Renderer2 在命名上带有 “2”,但它并不是简单的旧版本的更新。它是从头重新设计的、更先进、更灵活和更与时俱进的渲染器接口。这也是为什么现在推荐使用 Renderer2 而不是旧的 Renderer 接口。
Angular For Beginners - 27. Renderer2
Renderer2 是 ElementRef 的 production version, ElementRef 由于缺乏安全性,只适应于小型的个人项目。

1. 用法:
import {AfterViewInit,Component,ElementRef,OnInit,Renderer2,ViewChild,ViewChildren,
} from '@angular/core';
import { Pokemon } from 'src/app/models/pokemon';
import { PokemonService } from 'src/app/services/pokemon.service';@Component({selector: 'app-pokemon-list',templateUrl: './pokemon-list.component.html',styleUrls: ['./pokemon-list.component.css'],
})
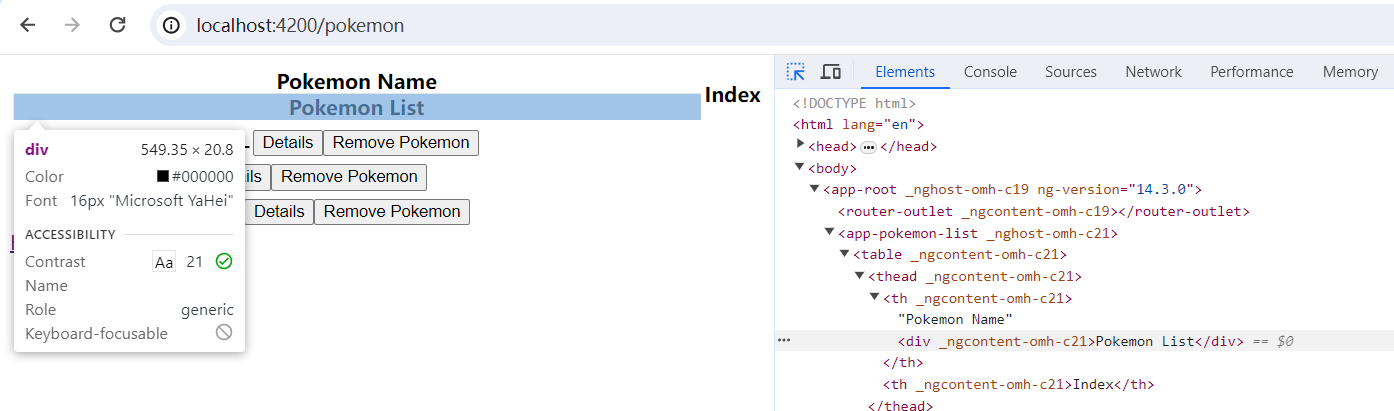
export class PokemonListComponent implements OnInit, AfterViewInit {pokemons: Pokemon[] = [];@ViewChildren('pokemonRef') pokemonRef!: ElementRef;@ViewChild('pokemonTh') pokemonTh!: ElementRef;constructor(private pokemonService: PokemonService,private renderer: Renderer2 // 引入 renderer2 !!!) {}// 使用 renderer2ngAfterViewInit(): void {console.log(this.pokemonTh);this.pokemonTh.nativeElement.innerText = 'Pokemon Name';const div=this.renderer.createElement('div');const text = this.renderer.createText('Pokemon List')this.renderer.appendChild(div, text);this.renderer.appendChild(this.pokemonTh.nativeElement, div)}handleRemove(event: Pokemon) {this.pokemons = this.pokemons.filter((pokemon: Pokemon) => {return pokemon.id !== event.id;});}ngOnInit(): void {this.pokemonService.getPokemons().subscribe((data: Pokemon[]) => {console.log(data);this.pokemons = data;});}
}
2. web 页面:
相关文章:

[Angular] 笔记 23:Renderer2 - ElementRef 的生产版本
chatgpt: Renderer2 简介 在 Angular 中,Renderer2 是一个服务,用于处理 DOM 操作的抽象层。它提供了一种安全的方式来操作 DOM,同时与平台无关,有助于维护应用程序的跨浏览器兼容性和安全性。 Renderer2 的作用是在 Angular 组…...

WEB:探索开源OFD.js技术应用
1、简述 OFD.js 是一个由开源社区维护的 JavaScript 库,专注于在浏览器中渲染和处理 OFD 文件。OFD 作为一种开放式的文档格式,被广泛应用于电子政务、电子合同等领域。OFD.js 的出现为开发者提供了一个强大的工具,使得在前端实现 OFD 文件的…...

平方根,又叫二次方根,表示为〔√ ̄〕
正在加载中... 平方根,又叫二次方根,表示为〔√ ̄〕,如: 平方根,又叫二次方根,表示为〔√ ̄〕,如:数学语言为:√ ̄164。语言描述为&…...

Springer Latex正文参考文献样式改为数字
用过爱斯唯尔的latex,正文参考文献都是数字,第一次用Springer Latex的参考文献竟然是authoryear,如下: 将这种样式变回序号样式: (1)使用这个documentclass(此为双栏) …...

六、typescript泛型使用
1.identity函数,这个函数会返回任何传入它的值,可以看作是echo命令 function identity(arg:number):number {return arg }或 使用any类型会导致这个函数可以接收任何类型的参数,这样会丢失一些信息,传入与返回类型应该是相同的 有…...

【快慢指针】26.删除有序数组中的重复项
题目 法1:快慢指针 基础解法,必须掌握!!! class Solution {public int removeDuplicates(int[] nums) {if (nums.length < 2) {return nums.length;}int slow 0, fast 1;while (fast < nums.length) {if (n…...
>)
爬虫工作量由小到大的思维转变---<第三十一章 Scrapy Redis 初启动/conn说明书)>
前言: 重点在读connection.py的源码,这个组件主要是用来连接的; 因为连接都无法做到,后面想更改点自定义就白扯了; 正文: 翻译版的connection.py源码: import sys import six from scrapy.utils.misc import load_object from . import defaults# 快捷方式映射 设置名称 -&…...

2023年山东省职业院校技能大赛高职组“软件测试”赛项-单元测试报告答案
任务四 单元测试 目录 任务四 单元测试 题目1: 题目2: 题目3:<...
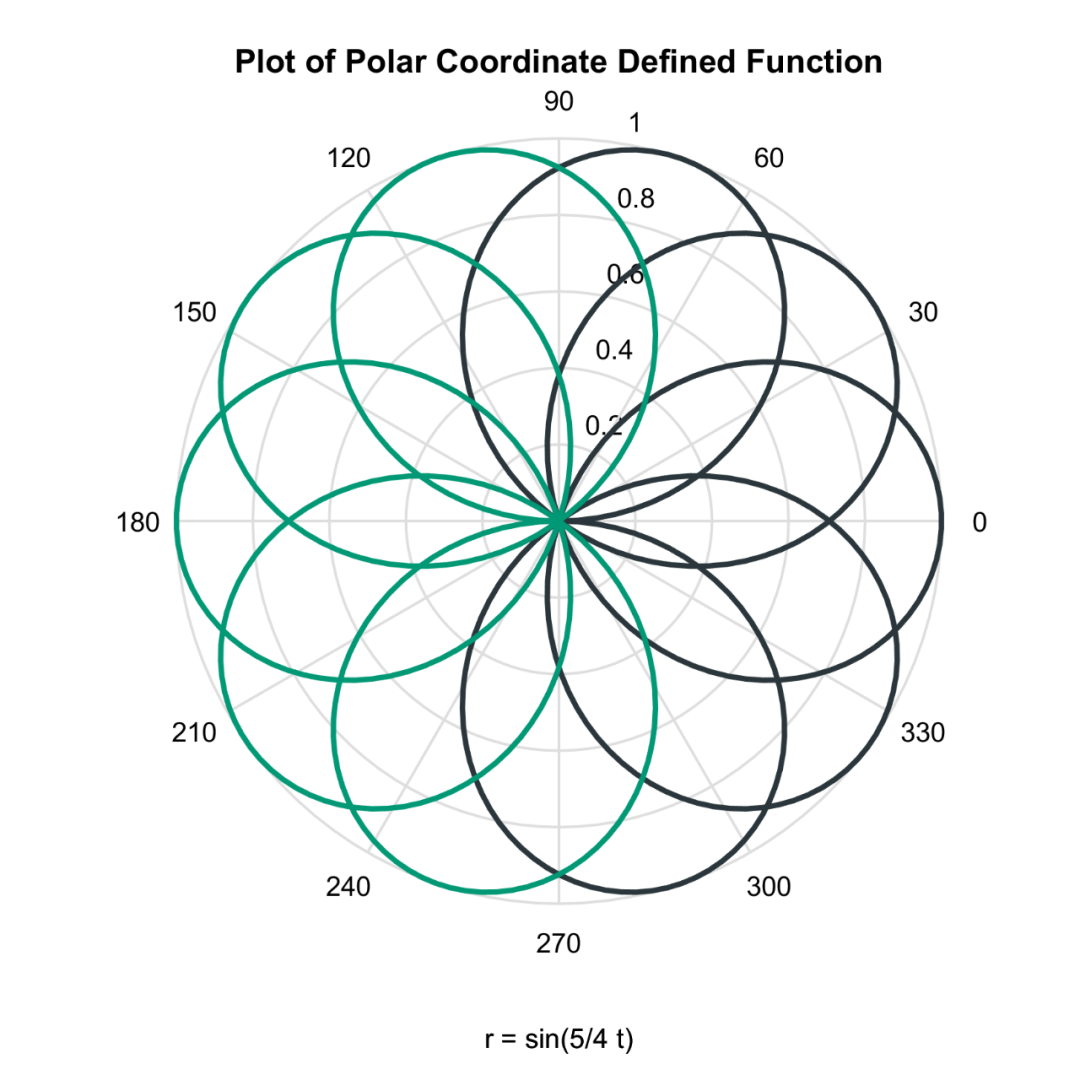
Matlab论文插图绘制模板第133期—函数极坐标折线图
在之前的文章中,分享了Matlab函数折线图的绘制模板: 函数三维折线图: 函数网格曲面图: 函数曲面图: 函数等高线图: 函数等高线填充图: 进一步,再来分享一下函数极坐标折线图。 先来…...

如何用 GPT 去分析Excel数据
背景 需要尝试分析 Excel 的内容,每月都需要进行相关的分析,固定化流程,因此尝试制作固化的脚本,方便后续的分析。 执行步骤 帮我写一段 python 代码,我需要区分一个.xlsx的数据。格式示例如下: ”这块自…...

力扣labuladong一刷day51天单调栈应用
力扣labuladong一刷day51天单调栈应用 一、239. 滑动窗口最大值 题目链接:https://leetcode.cn/problems/sliding-window-maximum/ 思路:滑动窗口最大值,既要维护加入的时间顺序,又要 class Solution {public int[] maxSliding…...

单片机相关知识点
在STM32上运行FreeRTOS,十分简练的小文章FreeRTOS(STM32CubeMX)_cubemx freertos-CSDN博客...
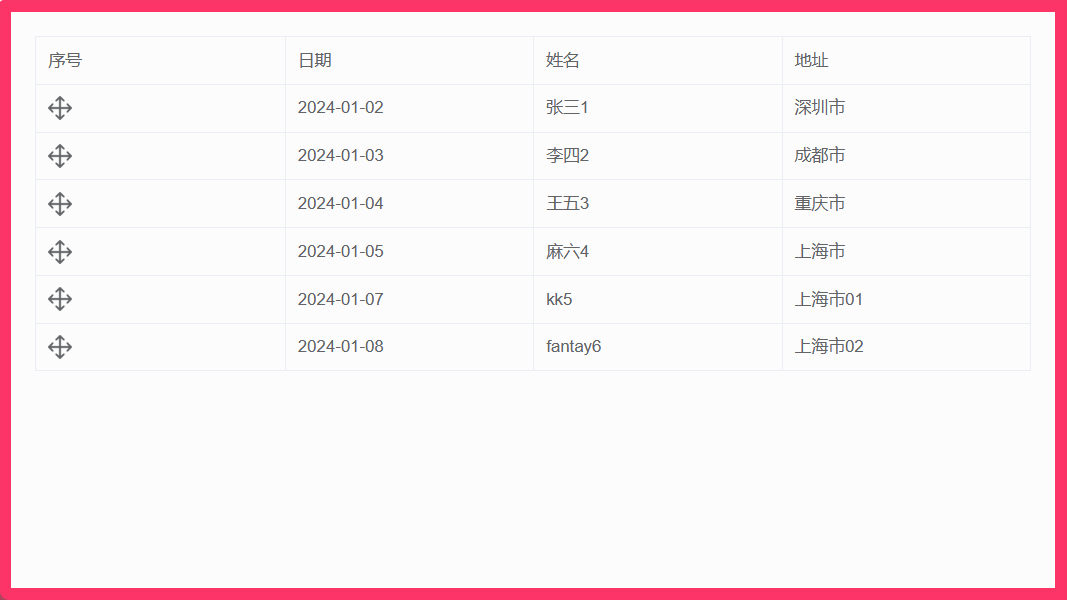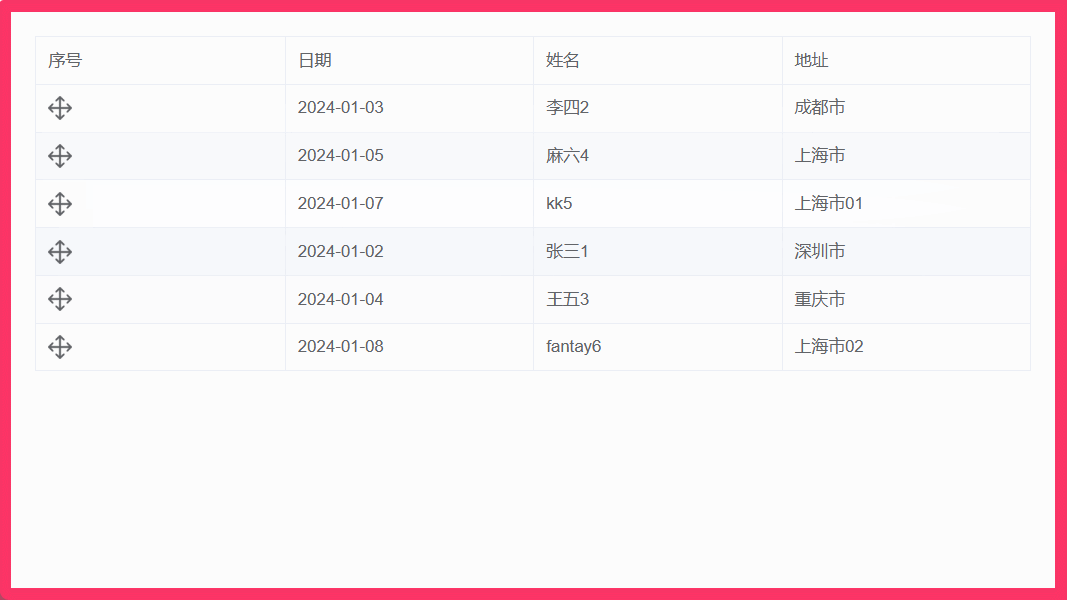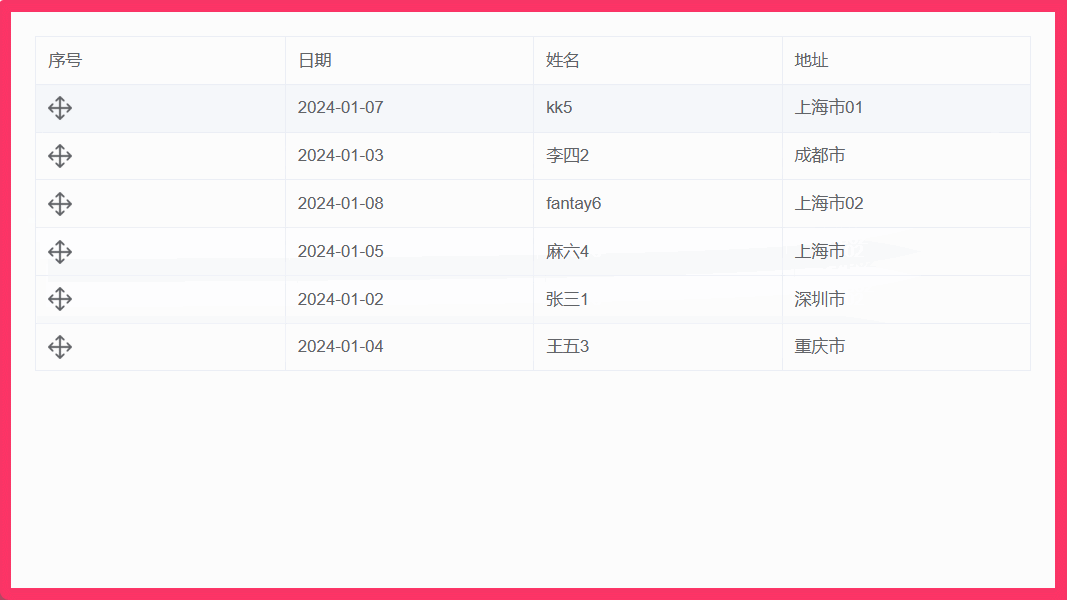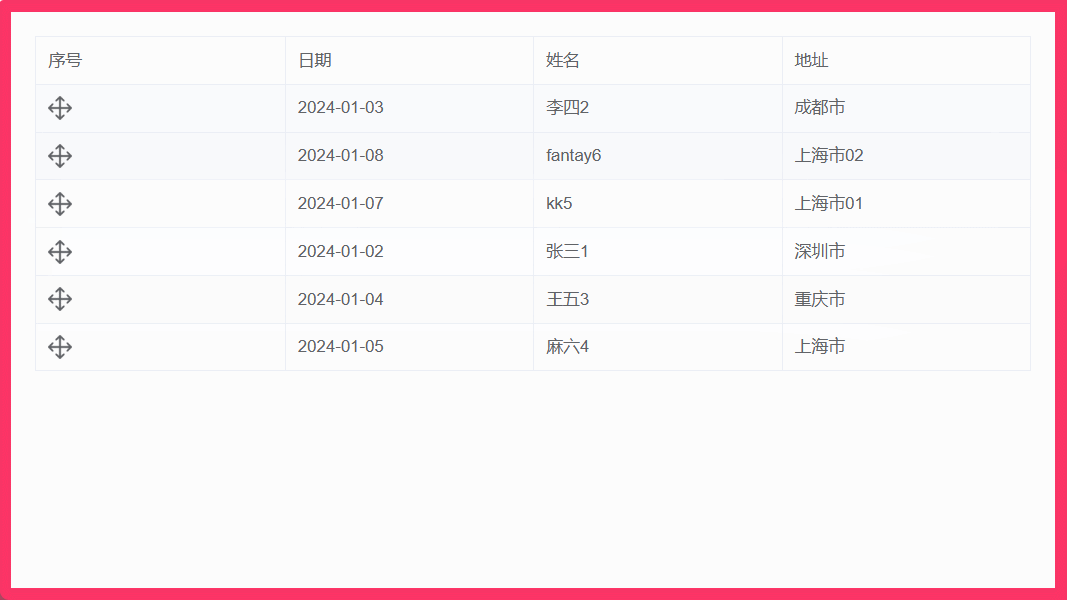
009:vue结合el-table实现表格行拖拽排序(基于sortablejs)
文章目录 1. 实现效果2. 安装 sortablejs 插件3. 完整组件代码4. 注意点 1. 实现效果 2. 安装 sortablejs 插件 sortablejs 更多用法 cnpm i --save sortablejs3. 完整组件代码 <template><div class"home"><div class"body"><el-ta…...
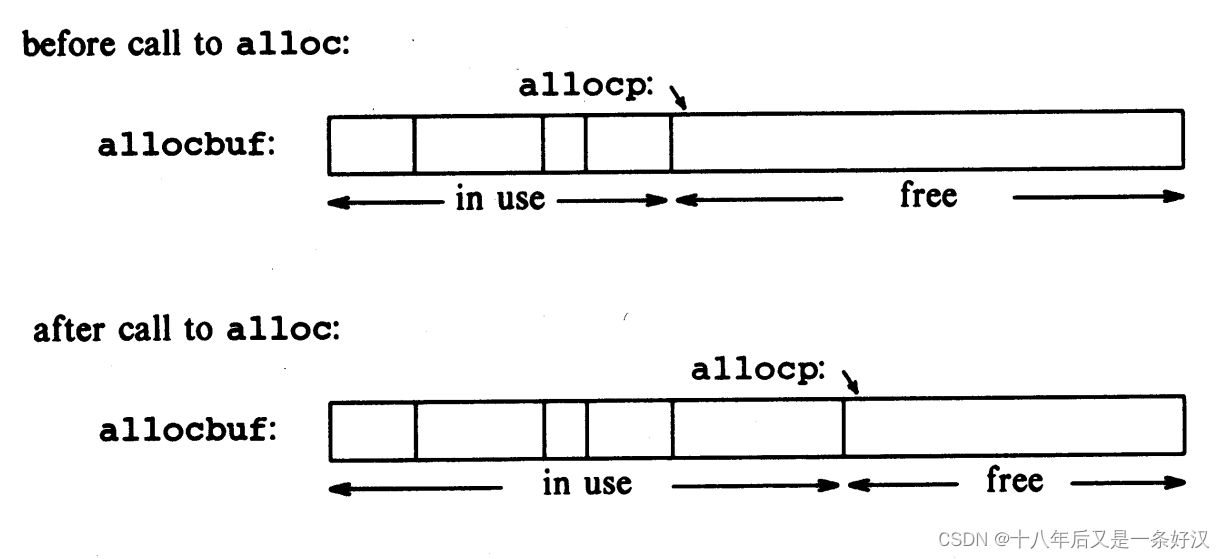
C语言KR圣经笔记 5.3指针和数组 5.4地址运算
5.3 指针和数组 在 C 语言中,指针和数组有着非常强的关联,强到应当把两者同时拿出来讨论。任何可以通过数组下标来做到的操作,也都能用指针来做到。而指针的版本通常会更快,但至少对初学者来说会更难理解。 如下声明 int a[10]…...
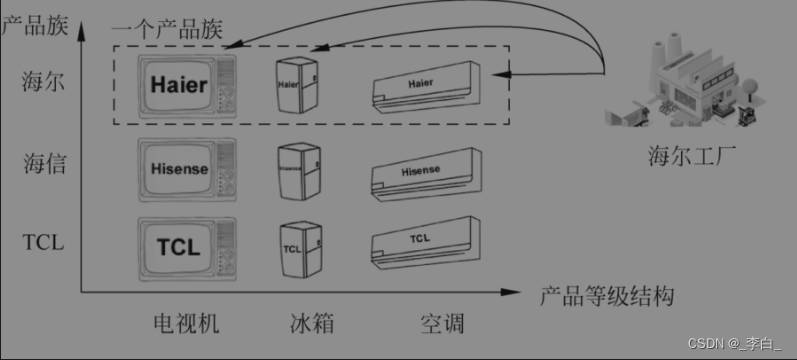
设计模式:简单工厂模式、工厂方法模式、抽象工厂模式
简单工厂模式、工厂方法模式、抽象工厂模式 1. 为什么需要工厂模式?2. 简单工厂模式2.1. 定义2.2. 代码实现2.3. 优点2.4. 缺点2.5. 适用场景 3. 工厂方法模式3.1. 有了简单工厂模式为什么还需要有工厂方法模式?3.2. 定义3.3. 代码实现3.4. 主要优点3.5.…...

Could not load library libcudnn_cnn_infer.so.8
报错: Could not load library libcudnn_cnn_infer.so.8. Error: /root/miniconda3/lib/python3.10/site-packages/torch/lib/libcudnn_cnn_infer.so.8: undefined symbol: _ZNK10cask_cudnn14BaseKernelInfo18minorCCVCompatibleENS_8SafeEnumINS_47ComputeCapa…...
ELement UI时间控件el-date-picker误差8小时解决办法
一、问题描述: 在项目中引用了elementui中的date-picker组件,选中的时间跟实际相差八小时,且格式不是自己想要的格式 <el-date-pickertype"date"placeholder"选择日期"format"yyyy/M/d"v-model"form…...

Linux日志论转
系统日志、审计日志、诊断日志 日志系统rsyslog 日志管理基础: rsyslog 日志管理 logrotate日志轮转常见的日志文件 #tail -f /var/log/messages #动态查看日志文件的尾部,系统主日志文件#tail -f /var/log/secure #记录认证、安全的日志…...

第7课 利用FFmpeg将摄像头画面与麦克风数据合成后推送到rtmp服务器
上节课我们已经拿到了摄像头数据和麦克风数据,这节课我们来看一下如何将二者合并起来推送到rtmp服务器。推送音视频合成流到rtmp服务器地址的流程如下: 1.创建输出流 //初始化输出流上下文 avformat_alloc_output_context2(&outFormatCtx, NULL, &…...
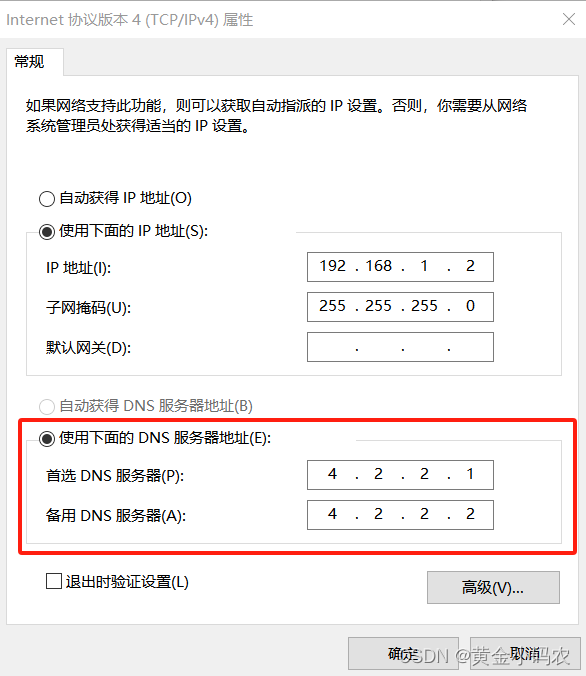
Microsoft Visual Studio 2022 install Project 下载慢
1. 关闭Internet 协议版本6 2. 如果没有效果,打开Internet 协议版本4,更改DNS 3. 在浏览器中下载后安装,下载地址如下: Microsoft Visual Studio Installer Projects 2022 - Visual Studio Marketplace 4. 安装时注意关闭vs&…...

shell脚本--常见案例
1、自动备份文件或目录 2、批量重命名文件 3、查找并删除指定名称的文件: 4、批量删除文件 5、查找并替换文件内容 6、批量创建文件 7、创建文件夹并移动文件 8、在文件夹中查找文件...

FFmpeg 低延迟同屏方案
引言 在实时互动需求激增的当下,无论是在线教育中的师生同屏演示、远程办公的屏幕共享协作,还是游戏直播的画面实时传输,低延迟同屏已成为保障用户体验的核心指标。FFmpeg 作为一款功能强大的多媒体框架,凭借其灵活的编解码、数据…...

iPhone密码忘记了办?iPhoneUnlocker,iPhone解锁工具Aiseesoft iPhone Unlocker 高级注册版分享
平时用 iPhone 的时候,难免会碰到解锁的麻烦事。比如密码忘了、人脸识别 / 指纹识别突然不灵,或者买了二手 iPhone 却被原来的 iCloud 账号锁住,这时候就需要靠谱的解锁工具来帮忙了。Aiseesoft iPhone Unlocker 就是专门解决这些问题的软件&…...

工程地质软件市场:发展现状、趋势与策略建议
一、引言 在工程建设领域,准确把握地质条件是确保项目顺利推进和安全运营的关键。工程地质软件作为处理、分析、模拟和展示工程地质数据的重要工具,正发挥着日益重要的作用。它凭借强大的数据处理能力、三维建模功能、空间分析工具和可视化展示手段&…...

如何将联系人从 iPhone 转移到 Android
从 iPhone 换到 Android 手机时,你可能需要保留重要的数据,例如通讯录。好在,将通讯录从 iPhone 转移到 Android 手机非常简单,你可以从本文中学习 6 种可靠的方法,确保随时保持连接,不错过任何信息。 第 1…...

HBuilderX安装(uni-app和小程序开发)
下载HBuilderX 访问官方网站:https://www.dcloud.io/hbuilderx.html 根据您的操作系统选择合适版本: Windows版(推荐下载标准版) Windows系统安装步骤 运行安装程序: 双击下载的.exe安装文件 如果出现安全提示&…...

算法笔记2
1.字符串拼接最好用StringBuilder,不用String 2.创建List<>类型的数组并创建内存 List arr[] new ArrayList[26]; Arrays.setAll(arr, i -> new ArrayList<>()); 3.去掉首尾空格...

rnn判断string中第一次出现a的下标
# coding:utf8 import torch import torch.nn as nn import numpy as np import random import json""" 基于pytorch的网络编写 实现一个RNN网络完成多分类任务 判断字符 a 第一次出现在字符串中的位置 """class TorchModel(nn.Module):def __in…...

React---day11
14.4 react-redux第三方库 提供connect、thunk之类的函数 以获取一个banner数据为例子 store: 我们在使用异步的时候理应是要使用中间件的,但是configureStore 已经自动集成了 redux-thunk,注意action里面要返回函数 import { configureS…...

Linux 内存管理实战精讲:核心原理与面试常考点全解析
Linux 内存管理实战精讲:核心原理与面试常考点全解析 Linux 内核内存管理是系统设计中最复杂但也最核心的模块之一。它不仅支撑着虚拟内存机制、物理内存分配、进程隔离与资源复用,还直接决定系统运行的性能与稳定性。无论你是嵌入式开发者、内核调试工…...
