Codeforces Good Bye 2023 A~E
A.2023(思维)
题意:
有一个序列 A = a 1 , a 2 , . . . , a n + k A = a_1, a_2, ..., a_{n + k} A=a1,a2,...,an+k,且这个序列满足 ∏ i = 1 n + k a i = 2023 \prod\limits_{i = 1}^{n + k}a_i = 2023 i=1∏n+kai=2023,而这个序列中的 k k k个数字被删除了,我们只知道剩下的数字序列 B = b 1 , b 2 , . . . , b n B = b_1, b_2, ..., b_{n} B=b1,b2,...,bn。
请你求出被删除的数字序列。
分析:
可以计算给出序列 B B B的乘积 v a l val val,如果 v a l val val是 2023 2023 2023的因子,那么只需要打印 2023 v a l , 1 , . . . , 1 ( k − 1 个 1 ) \frac{2023}{val}, 1, ..., 1(k - 1\text{个}1) val2023,1,...,1(k−1个1)。
如果 v a l val val不是 2023 2023 2023的因子,则无解。
代码:
#include<bits/stdc++.h>
using namespace std;int n, k, b[15];void solve() {cin >> n >> k;for (int i = 1; i <= n; i++) cin >> b[i];int ans = 2023;for (int i = 1; i <= n; i++) {if (ans % b[i] != 0) {cout << "No" << endl;return;}ans /= b[i];}cout << "Yes" << endl;cout << ans;for (int i = 2; i <= k; i++) {cout << " 1";}cout << endl;
}int main(){int Case;cin >> Case;while (Case--) {solve();}return 0;
}
B.Two Divisors(思维)
题意:
给出数字 x x x的最大和次大因子 a , b a,b a,b,请你求出数字 x x x。
- 规定 ( 1 ≤ a < b < x ) (1 \le a < b < x) (1≤a<b<x)
分析:
首先考虑 a , b a, b a,b的最小公倍数,如果最小公倍数与 b b b不相同,那么要求的数字 x x x就是 a , b a, b a,b的最小公倍数。
如果两数的最小公倍数就是 b b b,那么此时 b = a × p b = a \times p b=a×p,而 p p p必然为 x x x的最小素因子,因此, x = b × p = b × b a x = b \times p = b \times \frac{b}{a} x=b×p=b×ab
代码:
#include<bits/stdc++.h>
using namespace std;
typedef long long LL;void solve() {LL a, b;cin >> a >> b;LL gcd = __gcd(a, b);LL ans = a * b / gcd;if (ans == b) ans = ans / a * b;cout << ans << endl;
}int main(){int Case;cin >> Case;while (Case--) {solve();}return 0;
}
C.Training Before the Olympiad(思维)
题意:
给出一个包含 n n n个数字的序列 A = a 1 , a 2 , . . . , a n A = a_1, a_2, ..., a_n A=a1,a2,...,an。每位玩家在自己的回合可以进行以下操作:
-
如果数组中只剩下一个数字,游戏结束
-
否则,选择数组中两个元素 a i , a j ( i ≠ j ) a_i, a_j(i \ne j) ai,aj(i=j),删除这两个元素并将 ⌊ a i + a j 2 ⌋ \lfloor \frac{a_i + a_j}{2} \rfloor ⌊2ai+aj⌋放回数组中。
先手希望最后的数字尽可能大,后手希望最后的数字尽可能小,假设两人都极为聪明, 问:对于序列 A A A的所有前缀,进行游戏最后得到的数字是多少?
分析:
由于放回数组的元素为 ⌊ a i + a j 2 ⌋ \lfloor \frac{a_i + a_j}{2} \rfloor ⌊2ai+aj⌋,那么,只有被删除的两个数字恰好为一个奇数和一个偶数时才会导致最后的结果变小。
那么,先手为了使结果尽可能大,每次操作会优先将两个奇数删除,后手则会选择一奇一偶进行删除,以先后手均进行一次操作为一轮,那么每轮会删除 3 3 3个奇数,且答案会减少 1 1 1,即答案总共会减少 ⌊ 奇数个数 3 ⌋ \lfloor \frac{\text{奇数个数}}{3}\rfloor ⌊3奇数个数⌋。
那么最后,剩下的奇数个数就分为三种情况:
-
0个,已经没有奇数了,不影响答案
-
1个,此时只能将该奇数与偶数一起删除,会使答案再减少一
-
2个,先手可以将这两个奇数一起删除,因此不会再影响后续答案
对于 1 ∼ i 1 \sim i 1∼i的前缀的答案即为前 i i i个数字的前缀和减去减少的数量即可。
hint: 当只有一个数字时,直接输出该数字即可。
代码:
#include<bits/stdc++.h>
using namespace std;
typedef long long LL;LL a[100005];void solve() {int n;cin >> n;for (int i = 1; i <= n; i++) cin >> a[i];LL sum = a[1];int odd = 0, even = 0;if (a[1] % 2 == 0) even++;else odd++;cout << sum;for (int i = 2; i <= n; i++) {sum += a[i];if (a[i] % 2 == 0) even++;else odd++;if (odd % 3 == 1) cout << ' ' << sum - odd / 3 - 1;else cout << ' ' << sum - odd / 3;}cout << endl;
}int main(){int Case;cin >> Case;while (Case--) {solve();}return 0;
}
D.Mathematical Problem(找规律)
题意:
给出一个奇数 n n n,请你输出满足以下条件的 n n n个完全平方数:
-
这些完全平方数的十进制位数均为 n n n
-
所有完全平方数均可由其中一个完全平方数通过重排数字得到
分析:
对于 n = 1 n = 1 n=1,此时的答案选择 1 1 1即可。
对于 n = 3 n = 3 n=3,由样例可知答案可选: 169 , 196 , 961 169, 196, 961 169,196,961。
对于 n = i + 2 n = i + 2 n=i+2,不难发现,对于所有的 n = i n = i n=i的答案,均可通过乘上 100 100 100直接得到 i i i个满足要求的完全平方数。
证明: 若 b = c 2 ,则 b × 100 = ( c × 10 ) 2 \text{若}b = c^{2},\text{则}b \times 100 = (c \times 10)^{2} 若b=c2,则b×100=(c×10)2
但是这样只能获得 i i i个答案,还需要获得两个完全平方数,观察题目样例可以发现 169 = 1 3 2 , 961 = 3 1 2 169 = 13^{2}, 961 = 31^{2} 169=132,961=312。由于通过将 n = i n = i n=i的答案乘上 100 100 100得到 i i i个 n = i + 2 n = i + 2 n=i+2的答案,那么多出的两个数字均为 0 0 0,尝试将这两个 0 0 0加入 169 169 169和 961 961 961中,发现: 10609 = 10 3 2 , 90601 = 30 1 2 10609 = 103^{2}, 90601 = 301^{2} 10609=1032,90601=3012。继续尝试: 1006009 = 100 3 2 , 9006001 = 300 1 2 , . . . 1006009 = 1003^{2}, 9006001 = 3001^{2}, ... 1006009=10032,9006001=30012,...。
即:还差的两个完全平方数可以通过 169 , 961 169,961 169,961在百位和十位,十位和个位之间各添加 n − 3 2 \frac{n - 3}{2} 2n−3个 0 0 0得到。
预处理所有答案,对于每个询问输出预处理的答案即可。
代码:
#include<bits/stdc++.h>
using namespace std;
typedef long long LL;vector<string> ans[105];void init() {ans[1].push_back("1");ans[3].push_back("169");ans[3].push_back("196");ans[3].push_back("961");for (int i = 5; i <= 99; i += 2) {for (auto j : ans[i - 2]) {ans[i].push_back(j + "00");}string s1 = "1", s2 = "9";int len = (i - 3) / 2;for (int j = 0; j < len; j++) {s1 += '0', s2 += '0';}s1 += '6', s2 += '6';for (int j = 0; j < len; j++) {s1 += '0', s2 += '0';}s1 += '9', s2 += '1';ans[i].push_back(s1);ans[i].push_back(s2);}
}void solve() {int n;cin >> n;for (auto i : ans[n]) {cout << i << endl;}
}int main(){init();int Case;cin >> Case;while (Case--) {solve();}return 0;
}
E.Happy Life in University(DFS序,线段树)
题意:
有一棵根节点为 1 1 1的树,且树上每个节点均被涂上了一种颜色,你可以任取树上两点 u , v ( u ≠ v ) u, v(u \ne v) u,v(u=v),求最大的 d i f f ( u , l c a ( u , v ) ) × d i f f ( v , l c a ( u , v ) ) diff(u, lca(u, v)) \times diff(v, lca(u, v)) diff(u,lca(u,v))×diff(v,lca(u,v))。
其中:
-
d i f f ( u , v ) diff(u, v) diff(u,v)为点 u u u到点 v v v的路径上不同颜色的种类
-
l c a ( u , v ) lca(u, v) lca(u,v)为点 u u u和点 v v v的最近公共祖先
分析:
对于以节点 i i i为根节点的子树,若想以节点 i i i为最近公共祖先来计算答案,那么只能在不同的子树中取两个节点(由于路径越长颜色越多,实际被选中的一定为叶节点)。
那么当 l c a ( u , v ) = i lca(u, v) = i lca(u,v)=i时,实际上就会选择所有子树中路径包含颜色最多的前两棵子树,此时答案为这两棵子树的最大颜色数量的乘积。
因此,需要有一个数据结构来维护区间上的最大值,此时可以想到使用线段树进行维护。
想要使用线段树进行维护,那么就需要将树结构转化成线性的结构,这里可以使用 D f s Dfs Dfs序进行转化,优点是任意子树转化后在数组中均是连续的。
注意:转化过程中,需要计算根节点到该节点的路径上包含的不同颜色种类,并使用线段树进行单点更新。转化完整棵子树后,还需记录该子树最后遍历的节点所在的序号(记录该子树的存储范围)。
然后考虑查询每个节点为最近公共祖先时的最大价值,此时需要消除所有该子树的祖先节点带来的影响,可以通过线段树区间减法来进行,每次计算完一个节点后,对整棵子树通过 − 1 -1 −1的方式来消除该节点的影响,但考虑子树中可能还包含该颜色的节点,因此需要对该节点到达叶节点的所有不同路径上最近的颜色相同的节点再通过区间加法将该颜色加回来。
遍历完树后,就得到了最大的价值。
注意:多组输入,需要初始化(记录答案的变量要初始化为 1 1 1)。
代码:
#include<bits/stdc++.h>
using namespace std;
typedef long long LL;
const int N = 3e5 + 5e2;int n, cnt, tot, num[N][2], pre[N], col[N];
LL ans, lazy[N << 2], T[N << 2];
vector<int> G[N], nxt[N];void init() {ans = 1;cnt = tot = 0;for (int i = 0; i <= n; i++) {G[i].clear();nxt[i].clear();pre[i] = 0;}
}void pushup(int x) {T[x] = max(T[x << 1], T[x << 1 | 1]);
}void build(int l, int r, int x) {if (l == r) {lazy[x] = T[x] = 0;return;}lazy[x] = 0;int mid = l + r >> 1;build(l, mid, x << 1);build(mid + 1, r, x << 1 | 1);pushup(x);
}void pushdown(int x) {if (lazy[x]) {lazy[x << 1] += lazy[x];lazy[x << 1 | 1] += lazy[x];T[x << 1] += lazy[x];T[x << 1 | 1] += lazy[x];lazy[x] = 0;}
}void update (int l, int r, int UL, int UR, int x, int val) {if (l >= UL && r <= UR) {lazy[x] += val;T[x] += val;return;}pushdown(x);int mid = l + r >> 1;if (UL <= mid) update(l, mid, UL, UR, x << 1, val);if (UR > mid) update(mid + 1, r, UL, UR, x << 1 | 1, val);pushup(x);
}int query(int l, int r, int QL, int QR, int x) {if (l >= QL && r <= QR) {return T[x];}pushdown(x);int mid = l + r >> 1;int ans = 0;if (QL <= mid) ans = max(ans, query(l, mid, QL, QR, x << 1));if (QR > mid) ans = max(ans, query(mid + 1, r, QL, QR, x << 1 | 1));return ans;
}void dfs1(int root) {num[root][0] = ++tot;//节点root新的编号int p = pre[col[root]];//查看上一个该颜色的节点编号if (p == 0) cnt++;//第一次出现,颜色种类增加else nxt[p].push_back(root);//不是第一次出现,记录上个节点的一个后继为当前节点pre[col[root]] = root;update(1, n, tot, tot, 1, cnt);//更新for (auto i : G[root]) {dfs1(i);}/*回溯*/num[root][1] = tot;//节点root子树最后一个节点所在的编号if (p == 0) cnt--;pre[col[root]] = p;
}void dfs2(int root) {LL maxn = 1;for (auto i : G[root]) {LL val = query(1, n, num[i][0], num[i][1], 1);ans = max(ans, maxn * val);maxn = max(maxn, val);}update(1, n, num[root][0], num[root][1], 1, -1);//减去该颜色for (auto i : nxt[root]) {//拥有该颜色的子树加回来update(1, n, num[i][0], num[i][1], 1, 1);}for (auto i : G[root]) {dfs2(i);}
}void solve() {cin >> n;init();for (int i = 2; i <= n; i++) {int p;cin >> p;G[p].push_back(i);}for (int i = 1; i <= n; i++) {cin >> col[i];}build(1, n, 1);dfs1(1);dfs2(1);cout << ans << endl;
}int main(){ios::sync_with_stdio(false);int Case;cin >> Case;while (Case--) {solve();}return 0;
}
学习交流
以下为学习交流QQ群,群号: 546235402,每周题解完成后都会转发到群中,大家可以加群一起交流做题思路,分享做题技巧,欢迎大家的加入。

相关文章:

Codeforces Good Bye 2023 A~E
A.2023(思维) 题意: 有一个序列 A a 1 , a 2 , . . . , a n k A a_1, a_2, ..., a_{n k} Aa1,a2,...,ank,且这个序列满足 ∏ i 1 n k a i 2023 \prod\limits_{i 1}^{n k}a_i 2023 i1∏nkai2023,而这个序列中的 k k k个…...

【蓝桥杯】比赛大纲整理
枚举[1-3] 排序 (1)冒泡排序[2] (2)选择排序[3] (3)插入排序[3] 搜索(bfs, dfs)[1-5] 贪心[1-5] 模拟[1-3] 二分[2-5] DP(普通一维问题)[3-5] 高精度[1-5] 数据结构 (1)栈[2-4]&…...

探索 CodeWave低代码技术的魅力与应用
目录 前言1 低代码平台2 CodeWave简介3 CodeWave 的独特之处3.1 高保真还原交互视觉需求3.2 擅长复杂应用开发3.3 支持应用导出&独立部署3.4 金融级安全要求3.5 可集成性高3.6 可拓展性强 4 平台架构和核心功能4.1 数据模型设计4.2 页面设计4.3 逻辑设计4.4 流程设计4.5 接…...

《2023我的编程之旅》
一、背景 自从踏入编程的世界,我就像乘坐了一辆无法停下的列车,穿行在数据的丛林中,寻找解决问题的答案。编程不仅是我的职业,更是我表达自我、解决问题的工具。在这篇文章中,我将分享一段令人印象深刻的实战经历&…...
C++ 二进制图片的读取和blob插入mysql_stmt_init—新年第一课
关于二进制图片的读取和BLOB插入一共包含五步 第一步:初始化 MYSQL_STMT* stmt mysql_stmt_init(&mysql); 第二步:预处理sql语句 mysql_stmt_prepare(stmt,sql,sqllen); 第三步:绑定字段 mysql_stmt_bind_param(stmt,bind); 第四…...

向爬虫而生---Redis 基石篇2 <拓展Hash>
前言: 延续上一篇向爬虫而生---Redis 基石篇 <拓展str>-CSDN博客 这个章节拓展一下hash的玩法,主要是要挖一挖 ,啥时候用它最合适;让他并不是一无是处.. 正文: 哈希(Hash)数据结构是Redis中的一种常用的数据类型。它是一个键值…...
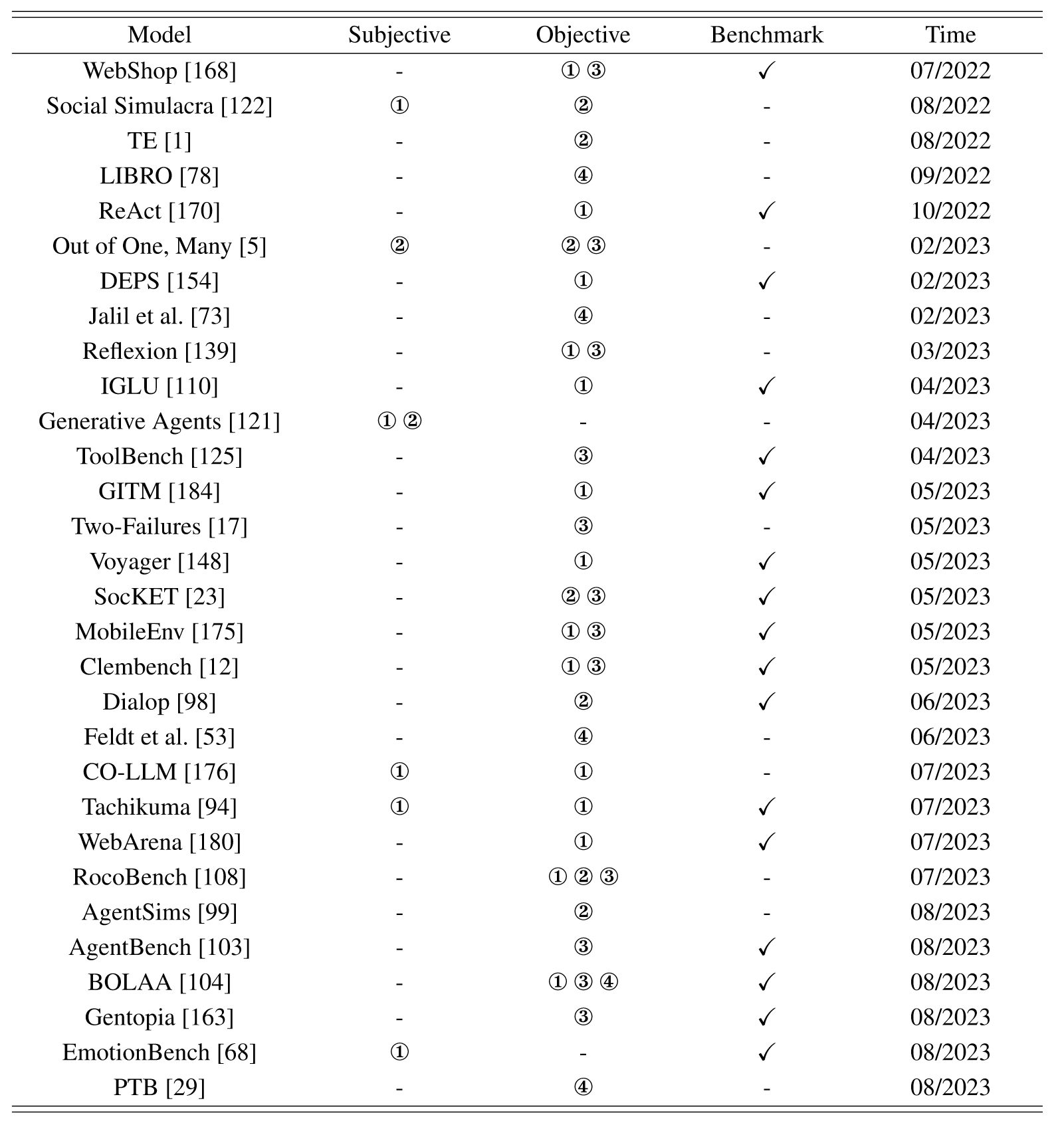
【论文精读】A Survey on Large Language Model based Autonomous Agents
A Survey on Large Language Model based Autonomous Agents 前言Abstract1 Introduction2 LLM-based Autonomous Agent Construction2.1 Agent Architecture Design2.1.1 Profiling Module2.1.2 Memory ModuleMemory StructuresMemory FormatsMemory Operations 2.1.3 Plannin…...
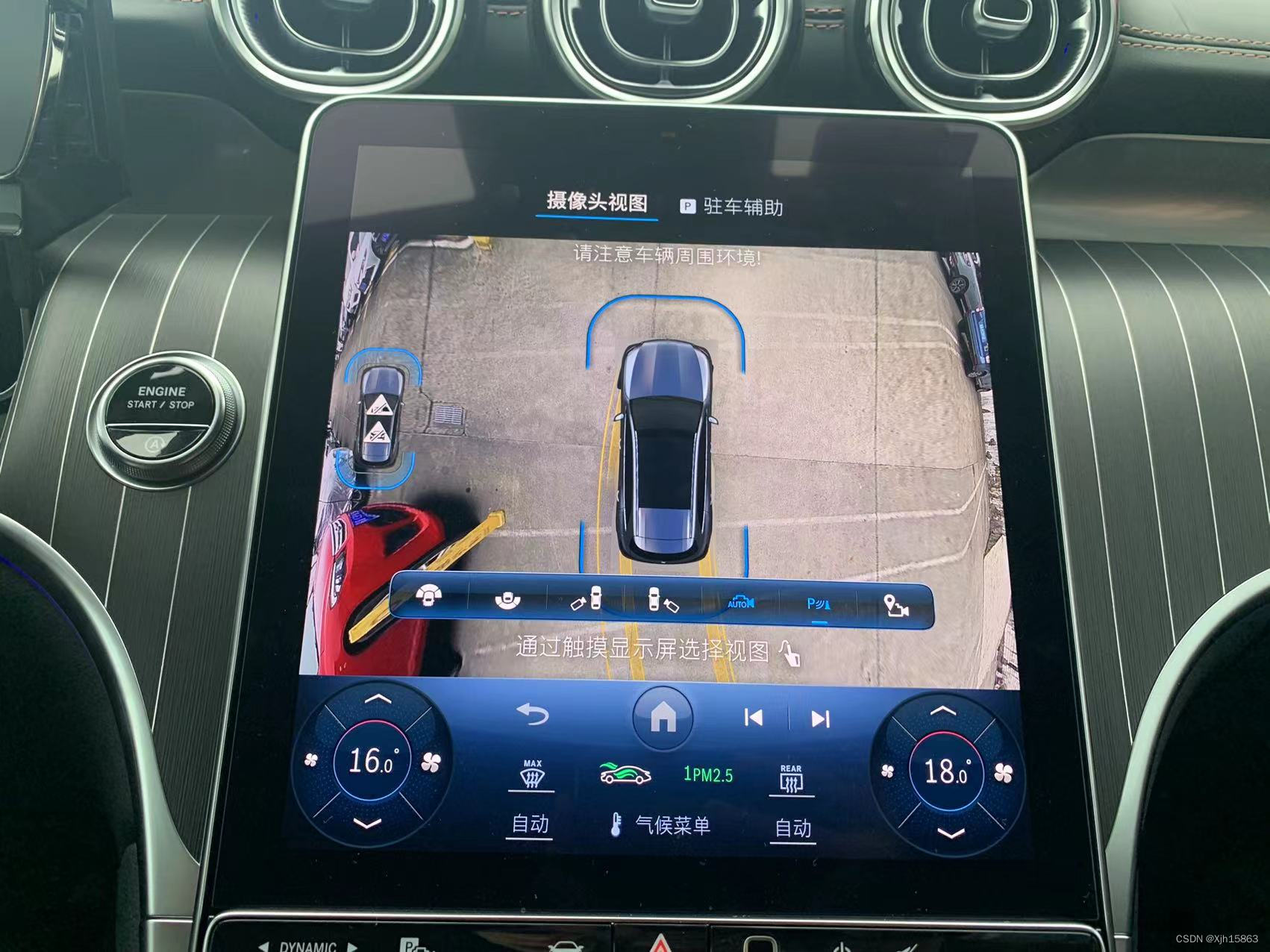
23款奔驰GLC260L升级原厂540全景影像 高清环绕的视野
嗨 今天给大家介绍一台奔驰GLC260L升级原厂360全景影像 新款GLC升级原厂360全景影像 也只需要安装前面 左右三个摄像头 后面的那个还是正常用的,不过不一样的是 升级完成之后会有多了个功能 那就是新款透明底盘,星骏汇小许Xjh15863 左右两边只需要更换后…...
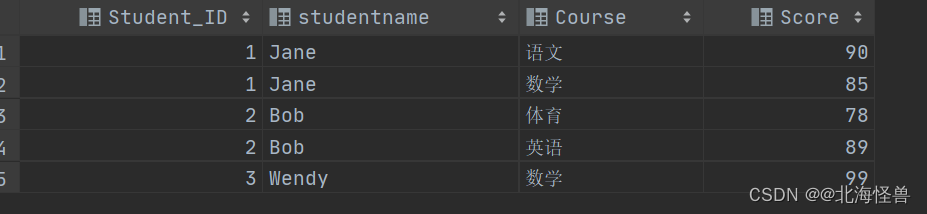
SQL 在已有表中修改列名的方法
文章目录 1. MySQL2. SQL Server3. Oracle / PostgreSQL Question: 假设有一张表 StudentInfo,表中有一个列名是 Student_Name ,想要把这个列名改成 StudentName 应该如何操作? 建表语句如下: --建表 if object_id(S…...
QT----Visual stdio翻金币案例,附源码
历经一个月,各种事情磕磕绊绊,终于结束了,自己还是太菜了 案例的文档写的教程已经很详细,这边主要是记录一些问题 github代码 gitee代码 1、图片无法加载 一开始加载首页图片和标题出不来,结果是paintEvent重写的字打…...

总结:浏览器解析html与执行JS之生命周期详解
总结:浏览器解析html与执行JS之生命周期详解 一浏览器解析html的生命周期:1.请求HTML文档:2接收响应:3构建DOM树:4加载外部资源:5DOMContentLoaded事件:6样式计算与布局:7绘制与渲染…...

aspose通过开始和结束位置关键词截取word另存为新文件
关键词匹配实体类: Data EqualsAndHashCode(callSuper false) public class TextConfig implements Serializable {private static final long serialVersionUID 1L;/*** 开始关键词,多个逗号分隔*/private String textStart ;/*** 结束关键词&#x…...

深入解析美颜SDK:绿幕抠图功能的算法原理
当下,美颜SDK绿幕抠图功能成为许多应用中不可或缺的一环。本文将深入解析美颜SDK中绿幕抠图功能的算法原理,揭示其背后的技术奥秘。 一、什么是美颜SDK绿幕抠图? 美颜SDK的绿幕抠图功能是一种通过计算机视觉技术,将视频或图像中…...

从有向带权图判断最短路径里各目标顶点顺序
对如下有向带权图,若采用迪杰斯特拉(Dijkstra)算法求从源点a到其他各顶点的最短路径,则得到的第一路径的目标顶点是b,第二条最短路径的目标顶点是c,后续得到的其余各最短路径的目标顶点依次是() A.d,e,f B.e,d,f C.f,d,e D.f,…...

鼠标驱动框架:模拟键盘按键
/* 参考: drivers\hid\usbhid\usbmouse.c */ #include <linux/kernel.h> #include <linux/slab.h> #include <linux/module.h> #include <linux/init.h> #include <linux/usb.h> #include <linux/input.h> #include <linux/hid.h>st…...
ES6之Promise的链式调用
✨ 专栏介绍 在现代Web开发中,JavaScript已经成为了不可或缺的一部分。它不仅可以为网页增加交互性和动态性,还可以在后端开发中使用Node.js构建高效的服务器端应用程序。作为一种灵活且易学的脚本语言,JavaScript具有广泛的应用场景&#x…...
HTML----JavaScript操作对象BOM对象
文章目录 目录 文章目录 本章要求 一.BOM模型概述 二.BOM核心:window对象 常用属性 常用方法: confirm() 案例 open ()close()案例 setTimeout( ) 案例 setInterval( ) 案例 document对象 练习 本章要求 了解BOM模型掌握BOM模型实际应用 一.BOM模型…...
)
隆道数智大会回顾|第13期《如何构建绿色产业供应链新生态》(完)
本期演讲嘉宾: 史文月 采购与供应链专家 邢庆峰 品类管理和质量管理专家 刘婷婷 中兴通讯供应链规划总监 张燕华 正大生物CIO 吴树贵 隆道公司总裁 本期演讲主题: 如何构建绿色产业供应链新生态 本期内容要点: 1.供应链管理的核心问…...
粒子群优化pso结合bp神经网络优化对csv文件预测matlab(3)
1.csv数据为密西西比数据集,获取数据集可以管我要,数据集内容形式如下图: 2.代码 这里参考的是b站的一位博主。 数据集导入教程在我的另一篇文章bp写过,需要的话可以去看一下 psobp.m close all clc%读取数据 inputX; outputY;…...

软性演员-评论家算法 SAC
软性演员-评论家算法 SAC 软性演员-评论家算法 SAC优势原理软性选择模型结构目标函数重参数化熵正则化代码实现 软性演员-评论家算法 SAC 优势原理 DDPG 的问题在于,训练不稳定、收敛差、依赖超参数、不适应复杂环境。 软性演员-评论家算法 SAC,更稳定…...

利用最小二乘法找圆心和半径
#include <iostream> #include <vector> #include <cmath> #include <Eigen/Dense> // 需安装Eigen库用于矩阵运算 // 定义点结构 struct Point { double x, y; Point(double x_, double y_) : x(x_), y(y_) {} }; // 最小二乘法求圆心和半径 …...

【Oracle APEX开发小技巧12】
有如下需求: 有一个问题反馈页面,要实现在apex页面展示能直观看到反馈时间超过7天未处理的数据,方便管理员及时处理反馈。 我的方法:直接将逻辑写在SQL中,这样可以直接在页面展示 完整代码: SELECTSF.FE…...
)
【HarmonyOS 5 开发速记】如何获取用户信息(头像/昵称/手机号)
1.获取 authorizationCode: 2.利用 authorizationCode 获取 accessToken:文档中心 3.获取手机:文档中心 4.获取昵称头像:文档中心 首先创建 request 若要获取手机号,scope必填 phone,permissions 必填 …...

云原生玩法三问:构建自定义开发环境
云原生玩法三问:构建自定义开发环境 引言 临时运维一个古董项目,无文档,无环境,无交接人,俗称三无。 运行设备的环境老,本地环境版本高,ssh不过去。正好最近对 腾讯出品的云原生 cnb 感兴趣&…...

算法岗面试经验分享-大模型篇
文章目录 A 基础语言模型A.1 TransformerA.2 Bert B 大语言模型结构B.1 GPTB.2 LLamaB.3 ChatGLMB.4 Qwen C 大语言模型微调C.1 Fine-tuningC.2 Adapter-tuningC.3 Prefix-tuningC.4 P-tuningC.5 LoRA A 基础语言模型 A.1 Transformer (1)资源 论文&a…...

Linux 中如何提取压缩文件 ?
Linux 是一种流行的开源操作系统,它提供了许多工具来管理、压缩和解压缩文件。压缩文件有助于节省存储空间,使数据传输更快。本指南将向您展示如何在 Linux 中提取不同类型的压缩文件。 1. Unpacking ZIP Files ZIP 文件是非常常见的,要在 …...

MinIO Docker 部署:仅开放一个端口
MinIO Docker 部署:仅开放一个端口 在实际的服务器部署中,出于安全和管理的考虑,我们可能只能开放一个端口。MinIO 是一个高性能的对象存储服务,支持 Docker 部署,但默认情况下它需要两个端口:一个是 API 端口(用于存储和访问数据),另一个是控制台端口(用于管理界面…...

【Linux】自动化构建-Make/Makefile
前言 上文我们讲到了Linux中的编译器gcc/g 【Linux】编译器gcc/g及其库的详细介绍-CSDN博客 本来我们将一个对于编译来说很重要的工具:make/makfile 1.背景 在一个工程中源文件不计其数,其按类型、功能、模块分别放在若干个目录中,mak…...
零知开源——STM32F103RBT6驱动 ICM20948 九轴传感器及 vofa + 上位机可视化教程
STM32F1 本教程使用零知标准板(STM32F103RBT6)通过I2C驱动ICM20948九轴传感器,实现姿态解算,并通过串口将数据实时发送至VOFA上位机进行3D可视化。代码基于开源库修改优化,适合嵌入式及物联网开发者。在基础驱动上新增…...

大模型真的像人一样“思考”和“理解”吗?
Yann LeCun 新研究的核心探讨:大语言模型(LLM)的“理解”和“思考”方式与人类认知的根本差异。 核心问题:大模型真的像人一样“思考”和“理解”吗? 人类的思考方式: 你的大脑是个超级整理师。面对海量信…...
