从有向带权图判断最短路径里各目标顶点顺序
对如下有向带权图,若采用迪杰斯特拉(Dijkstra)算法求从源点a到其他各顶点的最短路径,则得到的第一路径的目标顶点是b,第二条最短路径的目标顶点是c,后续得到的其余各最短路径的目标顶点依次是()
A.d,e,f
B.e,d,f
C.f,d,e
D.f,e,d

首先,先看除了a还有5个顶点,那么就是要走5趟。
在下面表格列出b、c、d、e、f 以及一两三四五趟,最后一行写集合。
| 顶点 | 一趟 | 两趟 | 三趟 | 四趟 | 五趟 |
| b | |||||
| c | |||||
| d | |||||
| e | |||||
| f | |||||
| 集合 |

- 在一开始我自己定义:
- 顶点a至b算一趟,顶点a至c也算一趟
- 以此类推,例如后面讲述的顶点a至b至c算两趟
- 然后再看,从a出发,首先接触的是b、c,那么分别写下到b和c的距离。
- 其他顶点对a来说一趟接触不到,那么我们就写无穷,即∞。
- 其中,(a,b)最短,距离为2,那么得出结论:集合就是{a,b}
- 由于顶点c这次没被引用,于是将(a,c)5先搁置至二趟(但每一次搁置到后面一趟需检验a至c是不是最短的,还有没有从a至c更加短的距离,详情看后面几轮)
| 顶点 | 一趟 | 两趟 | 三趟 | 四趟 | 五趟 |
| b | (a,b)2 | ||||
| c | (a,c)5 | (a,c)5 | |||
| d | ∞ | ||||
| e | ∞ | ||||
| f | ∞ | ||||
| 集合 | {a,b} |

- 然后再看,从a至b出发,能走两趟的就只有(a,b,c)和(a,b,d),此时(a,b,c)距离为3,(a,b,d)距离为5。
- 上一趟的(a,c)搁置到二趟需检验a至c是不是最短的,还有没有从a至c更加短的路线,哦有,就是我们刚才写的(a,b,c),(a,c)距离为5,(a,b,c)距离才3,那么就用(a,b,c)代替(a,c)。
- 此时(a,b,c)距离为3,(a,b,d)距离为5
- 那么最短的就是(a,b,c)
- 那么集合就是{a,b,c}
| 顶点 | 一趟 | 两趟 | 三趟 | 四趟 | 五趟 |
| b | (a,b)2 | ||||
| c | (a,c)5 | (a,c)5/(a,b,c)3 | |||
| d | ∞ | (a,b,d)5 | |||
| e | ∞ | ∞ | |||
| f | ∞ | ∞ | |||
| 集合 | {a,b} | {a,b,c} |

- 然后再看,此时b和c都被引用了,就剩d、e、f,即从a至b至c出发,能走三趟的,能接触到的就是d、e、f
- 此时三趟为(a,b,c,d)距离为6,(a,b,c,e)距离为7,(a,b,c,f)距离为4。
- (a,b,d)因为上一趟距离长没有选上,虽不是最短,但可以先搁置到这一趟继续写,但搁置到这一趟需检验a至d是不是最短的,还有没有从a至d更加短的路线,哦没有,还是(a,b,d),(a,b,c,d)距离为6,(a,b,d)距离才5,那么就保留(a,b,d)。
- 此时三趟为(a,b,d)距离为5,(a,b,c,e)距离为7,(a,b,c,f)距离为4,(a,b,c,f)最短,选(a,b,c,f)。
- 故集合为{a,b,c,f}
| 顶点 | 一趟 | 两趟 | 三趟 | 四趟 | 五趟 |
| b | (a,b)2 | ||||
| c | (a,c)5 | (a,c)5/(a,b,c)3 | |||
| d | ∞ | (a,b,d)5 | (a,b,d)5/(a,b,c,d)6 | ||
| e | ∞ | ∞ | (a,b,c,e)7 | ||
| f | ∞ | ∞ | (a,b,c,f)4 | ||
| 集合 | {a,b} | {a,b,c} | {a,b,c,f} |

- 然后再看,从a至b至c至f出发,能走四趟的,能接触到的就是d、e
- (a,b,d)是从二趟开始搁置到这一趟,因为已经检验过了所以不用检验,而(a,b,c,e)是从三趟才开始搁置的,还没检验过,检验一下,(a,b,c,e)距离为7,(a,b,d,e)距离为6,(a,c,e)距离为9,(a,b,c,d,e)距离为7,故(a,b,d,e)最短,用(a,b,d,e)替代这几个
- 然而虽然(a,b,d,e)距离为6,(a,b,d)5距离为5而已,故还是选(a,b,d)。
- 故集合为{a,b,c,f,d}
| 顶点 | 一趟 | 两趟 | 三趟 | 四趟 | 五趟 |
| b | (a,b)2 | ||||
| c | (a,c)5 | (a,c)5/(a,b,c)3 | |||
| d | ∞ | (a,b,d)5 | (a,b,d)5/(a,b,c,d)6 | (a,b,d)5 | |
| e | ∞ | ∞ | (a,b,c,e)7 | (a,b,c,e)7/(a,b,d,e)6/(a,c,e)9/(a,b,c,d,e)7 | |
| f | ∞ | ∞ | (a,b,c,f)4 | ||
| 集合 | {a,b} | {a,b,c} | {a,b,c,f} | {a,b,c,f,d} |

- 然后再看,此时就剩e,即从a至b至c至f至d出发,能走五趟的,能接触到的就只有e了
- (a,b,d,e)是从四趟开始搁置到这一趟,因为已经检验过了所以不用检验。
- 故集合为{a,b,c,f,d,e}
| 顶点 | 一趟 | 两趟 | 三趟 | 四趟 | 五趟 |
| b | (a,b)2 | ||||
| c | (a,c)5 | (a,c)5/(a,b,c)3 | |||
| d | ∞ | (a,b,d)5 | (a,b,d)5/(a,b,c,d)6 | (a,b,d)5 | |
| e | ∞ | ∞ | (a,b,c,e)7 | (a,b,c,e)7/(a,b,d,e)6/(a,c,e)9/(a,b,c,d,e)7 | (a,b,d,e)6 |
| f | ∞ | ∞ | (a,b,c,f)4 | ||
| 集合 | {a,b} | {a,b,c} | {a,b,c,f} | {a,b,c,f,d} | {a,b,c,f,d,e} |
故后续得到的其余各最短路径的目标顶点依次是{a,b,c,f,d,e}
相关文章:

从有向带权图判断最短路径里各目标顶点顺序
对如下有向带权图,若采用迪杰斯特拉(Dijkstra)算法求从源点a到其他各顶点的最短路径,则得到的第一路径的目标顶点是b,第二条最短路径的目标顶点是c,后续得到的其余各最短路径的目标顶点依次是() A.d,e,f B.e,d,f C.f,d,e D.f,…...

鼠标驱动框架:模拟键盘按键
/* 参考: drivers\hid\usbhid\usbmouse.c */ #include <linux/kernel.h> #include <linux/slab.h> #include <linux/module.h> #include <linux/init.h> #include <linux/usb.h> #include <linux/input.h> #include <linux/hid.h>st…...
ES6之Promise的链式调用
✨ 专栏介绍 在现代Web开发中,JavaScript已经成为了不可或缺的一部分。它不仅可以为网页增加交互性和动态性,还可以在后端开发中使用Node.js构建高效的服务器端应用程序。作为一种灵活且易学的脚本语言,JavaScript具有广泛的应用场景&#x…...
HTML----JavaScript操作对象BOM对象
文章目录 目录 文章目录 本章要求 一.BOM模型概述 二.BOM核心:window对象 常用属性 常用方法: confirm() 案例 open ()close()案例 setTimeout( ) 案例 setInterval( ) 案例 document对象 练习 本章要求 了解BOM模型掌握BOM模型实际应用 一.BOM模型…...
)
隆道数智大会回顾|第13期《如何构建绿色产业供应链新生态》(完)
本期演讲嘉宾: 史文月 采购与供应链专家 邢庆峰 品类管理和质量管理专家 刘婷婷 中兴通讯供应链规划总监 张燕华 正大生物CIO 吴树贵 隆道公司总裁 本期演讲主题: 如何构建绿色产业供应链新生态 本期内容要点: 1.供应链管理的核心问…...
粒子群优化pso结合bp神经网络优化对csv文件预测matlab(3)
1.csv数据为密西西比数据集,获取数据集可以管我要,数据集内容形式如下图: 2.代码 这里参考的是b站的一位博主。 数据集导入教程在我的另一篇文章bp写过,需要的话可以去看一下 psobp.m close all clc%读取数据 inputX; outputY;…...

软性演员-评论家算法 SAC
软性演员-评论家算法 SAC 软性演员-评论家算法 SAC优势原理软性选择模型结构目标函数重参数化熵正则化代码实现 软性演员-评论家算法 SAC 优势原理 DDPG 的问题在于,训练不稳定、收敛差、依赖超参数、不适应复杂环境。 软性演员-评论家算法 SAC,更稳定…...

Nginx多域名部署多站点
目录 1.修改配置文件nginx.conf 2. 修改hosts文件 1.修改配置文件nginx.conf 在配置文件的 server_name 处修改成自己需要的域名,然后保存退出 j 查看语法是否错误,然后重启nginx nginx -t # 查看语法是否正确 systemctl restart nginx # 重启nginx …...

Java的常规面试题
Java的面试题主要涉及Java基础知识、并发编程、集合原理、JVM原理、I/O与网络编程、设计模式、互联网常用框架等多个领域[6]。一些常见的面试问题包括: 1. 面向对象的特征:继承、封装和多态性。 2. 访问修饰符public、private、protected以及默认时的区别…...

大数据技术发展史
文章目录 Google论文HadoopHive大数据生态 Google论文 今天我们常说的大数据技术,其实起源于Google在2004年前后发表的三篇论文,也就是我们经常听到的“三驾马车”,分别是分布式文件系统GFS、大数据分布式计算框架MapReduce和NoSQL数据库系统…...

linux常见基础指令
入门常见基础指令 ls、stat、 pwd 、cd、tree、 whoami、 touch、 mkdir、 rm 、 man、 cp、mv、cat、tac、echo、>、 >>、 < 、more、 less、 head、 tail、date、 cal、 find、 which、alias、whereis、grep、zip与unzip、 tar、bc、uname、xargs... 热键Tab、…...

“人家赚那么多”系列01:如何练习?练什么?
01 如何练习?练习什么? 今年计划重点围绕「在不骗自己的前提下,如何才能把事儿彻底做好,并做得有声有色?」为主题来写点儿东西,聊聊我是怎么做的,如何通过一些有效的方法来不断优化自己的。 想把…...

【Android】使用android studio查看内置数据库信息
要使用Android Studio查看内置数据库信息,可以按照以下步骤进行操作: 打开Android Studio并打开你的项目。 在左侧的Project窗口中,找到并展开你的app模块。 找到并展开"app" > "src" > "main"文件夹。…...

PHP开发日志 ━━ 基于PHP和JS的AES相互加密解密方法详解(CryptoJS) 适合CryptoJS4.0和PHP8.0
最近客户在做安全等保,需要后台登录密码采用加密方式,原来用个base64变形一下就算了,现在不行,一定要加密加key加盐~~ 前端使用Cypto-JS加密,传输给后端使用PHP解密,当然,前端虽然有key有盐&…...

2021-01-03 excel实现列递增,行保持不变
需求:excel文档数据操作的时候发现自动递增只能实现列不变行号递增 我这里里需要的是列递增行不变 解决方式:通过一些函数的组合使用 INDIRECT("驻场明细!"&CHAR(ROW()62)&ROW(驻场明细!A$28)) INDIRECT()函数的使用: INDI…...

[Python]两个杯子取水问题
利用两个杯子巧取三升水: 今天的这个趣味数学小游戏是利用两个没有刻度的水杯,巧妙地取出三升水来。 题目的条件是:一个总容量为6升的杯子和一个总容量为5升的杯子,同时面前有无限容量的水供你使用。不借助其它任何的容器…...

C++汇编语言学习计划
前几天买了某游戏的外挂,感觉外挂在我计算机上进行了不少操作,我想一探究竟,可是只有exe,没办法,翻译成汇编我也看不懂,索性来简单学习下。访问Chatgpt4,给了如下学习计划。 要从零开始学习C生成…...
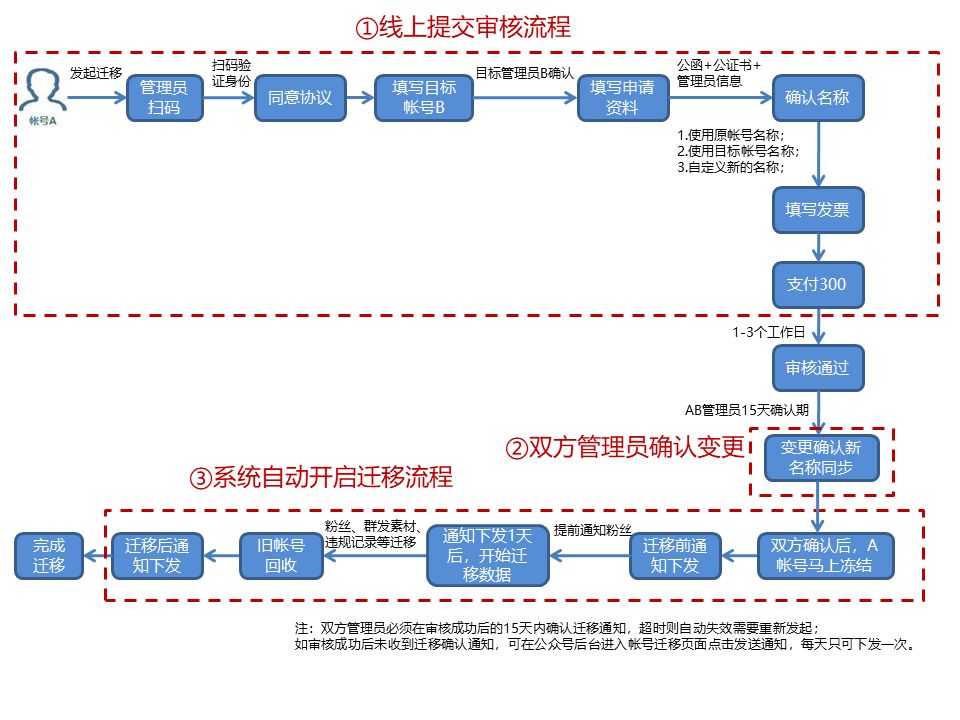
微信服务号升级订阅号条件
服务号和订阅号有什么区别?服务号转为订阅号有哪些作用?首先我们要看一下服务号和订阅号的主要区别。1、服务号推送的消息没有折叠,消息出现在聊天列表中,会像收到消息一样有提醒。而订阅号推送的消息是折叠的,“订阅号…...
SpringBoot整合mybatis多数据源
废话不多说先上结果 对应数据库 首先导入所需的mybatis、mysql和lombok依赖 <dependency><groupId>org.mybatis.spring.boot</groupId><artifactId>mybatis-spring-boot-starter</artifactId><version>2.2.2</version></dependen…...
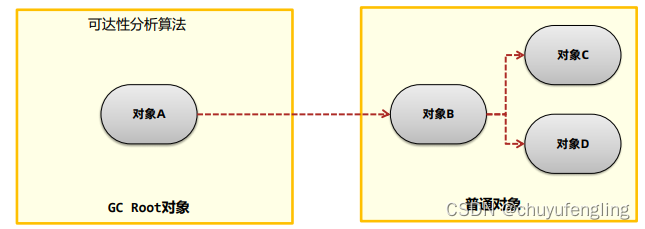
垃圾收集器与内存分配策略
内存分配和回收原则 对象优先在Eden区分配 大对象直接进入老年代 长期存活的对象进入老年代 什么是内存泄漏 不再使用的对象在系统中未被回收,内存泄漏的积累可能会导致内存溢出 自动垃圾回收与手动垃圾回收 自动垃圾回收:由虚拟机来自动回收对象…...

深度学习在微纳光子学中的应用
深度学习在微纳光子学中的主要应用方向 深度学习与微纳光子学的结合主要集中在以下几个方向: 逆向设计 通过神经网络快速预测微纳结构的光学响应,替代传统耗时的数值模拟方法。例如设计超表面、光子晶体等结构。 特征提取与优化 从复杂的光学数据中自…...

SkyWalking 10.2.0 SWCK 配置过程
SkyWalking 10.2.0 & SWCK 配置过程 skywalking oap-server & ui 使用Docker安装在K8S集群以外,K8S集群中的微服务使用initContainer按命名空间将skywalking-java-agent注入到业务容器中。 SWCK有整套的解决方案,全安装在K8S群集中。 具体可参…...

理解 MCP 工作流:使用 Ollama 和 LangChain 构建本地 MCP 客户端
🌟 什么是 MCP? 模型控制协议 (MCP) 是一种创新的协议,旨在无缝连接 AI 模型与应用程序。 MCP 是一个开源协议,它标准化了我们的 LLM 应用程序连接所需工具和数据源并与之协作的方式。 可以把它想象成你的 AI 模型 和想要使用它…...

【磁盘】每天掌握一个Linux命令 - iostat
目录 【磁盘】每天掌握一个Linux命令 - iostat工具概述安装方式核心功能基础用法进阶操作实战案例面试题场景生产场景 注意事项 【磁盘】每天掌握一个Linux命令 - iostat 工具概述 iostat(I/O Statistics)是Linux系统下用于监视系统输入输出设备和CPU使…...

[10-3]软件I2C读写MPU6050 江协科技学习笔记(16个知识点)
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16...
的原因分类及对应排查方案)
JVM暂停(Stop-The-World,STW)的原因分类及对应排查方案
JVM暂停(Stop-The-World,STW)的完整原因分类及对应排查方案,结合JVM运行机制和常见故障场景整理而成: 一、GC相关暂停 1. 安全点(Safepoint)阻塞 现象:JVM暂停但无GC日志,日志显示No GCs detected。原因:JVM等待所有线程进入安全点(如…...

Docker 本地安装 mysql 数据库
Docker: Accelerated Container Application Development 下载对应操作系统版本的 docker ;并安装。 基础操作不再赘述。 打开 macOS 终端,开始 docker 安装mysql之旅 第一步 docker search mysql 》〉docker search mysql NAME DE…...

Windows安装Miniconda
一、下载 https://www.anaconda.com/download/success 二、安装 三、配置镜像源 Anaconda/Miniconda pip 配置清华镜像源_anaconda配置清华源-CSDN博客 四、常用操作命令 Anaconda/Miniconda 基本操作命令_miniconda创建环境命令-CSDN博客...

android RelativeLayout布局
<?xml version"1.0" encoding"utf-8"?> <RelativeLayout xmlns:android"http://schemas.android.com/apk/res/android"android:layout_width"match_parent"android:layout_height"match_parent"android:gravity&…...

Ubuntu系统复制(U盘-电脑硬盘)
所需环境 电脑自带硬盘:1块 (1T) U盘1:Ubuntu系统引导盘(用于“U盘2”复制到“电脑自带硬盘”) U盘2:Ubuntu系统盘(1T,用于被复制) !!!建议“电脑…...
