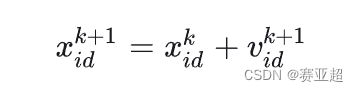粒子群优化pso结合bp神经网络优化对csv文件预测matlab(3)
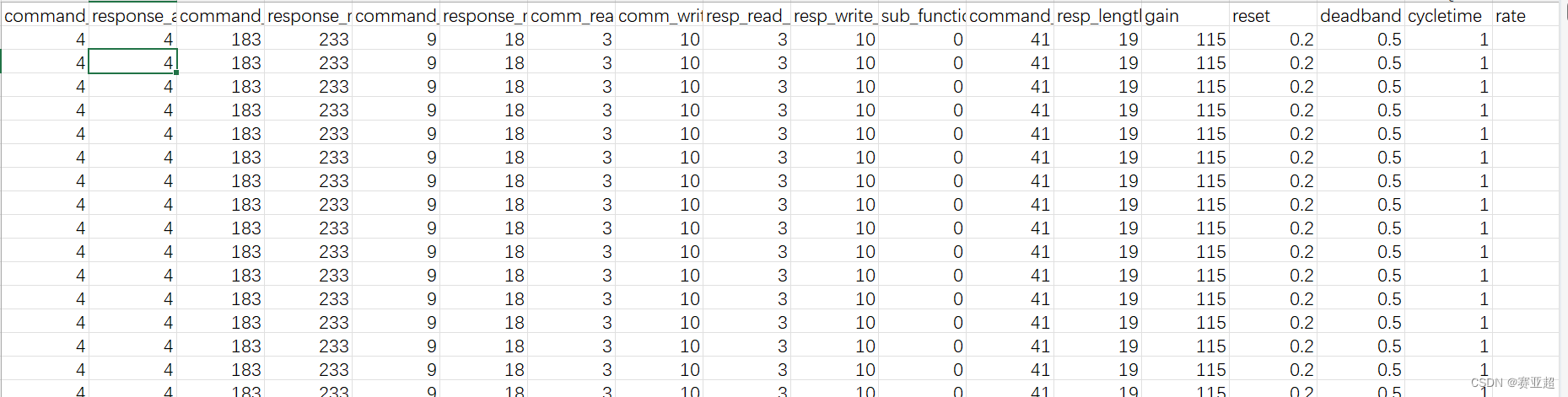
1.csv数据为密西西比数据集,获取数据集可以管我要,数据集内容形式如下图:
2.代码
这里参考的是b站的一位博主。
数据集导入教程在我的另一篇文章bp写过,需要的话可以去看一下

psobp.m
close all
clc%读取数据
input=X;
output=Y;%10000行1列
%设置训练数据与测试数据
input_train=input(1:8000,:)';
output_train=output(1:8000,:)';
input_test=input(8001:10000,:)';
output_test=output(8001:10000,:)';%2000列1行
%节点个数
inputnum=26;%输入层节点数量
hiddennum=12;%隐藏层节点数量
outputnum=1;%输出层节点数量
w1num=inputnum*hiddennum;%输入层到隐藏层的权值个数
w2num=outputnum*hiddennum;%输出层到隐藏层的权值个数
N=w1num+hiddennum+w2num+outputnum;%待优化的变量个数
%训练数据归一化
[inputn,inputps]=mapminmax(input_train);
[outputn,outputps]=mapminmax(output_train);
%%定义pso算法参数
E0=0.001;%允许误差
MaxNum=10;%粒子最大迭代次数
narvs=N;%目标函数的子变量个数
particlesize=10;%粒子群规模
c1=2;%个体经验学习因子
c2=2;%社会经验学习因子
w=0.6;%惯性因子
vmax=0.8;%粒子最大飞行速度
x=-5+10*rand(particlesize,narvs);%粒子所在位置,规模是粒子群数和参数需求数设置x的取值范围[-5,5]
v=2*rand(particlesize,narvs);%粒子飞行速度,生成每个粒子飞行速度,只有一个变量,所以速度是一维的
trace=zeros(N+1,MaxNum);%寻优结果的初始值
objv=objfun(x,input_train,output_train,input_test,output_test);%计算目标函数值
personalbest_x=x;%用于存储个体最优,存储每个粒子经历的x值
personalbest_faval=objv;%存储个体最优的y,每个个体的误差的群体
[globalbest_faval,i]=min(personalbest_faval);
globalbest_x=personalbest_x(i,:);%全局最优的x
k=1;%开始迭代
while k<=MaxNumobjv=objfun(x,input_train,output_train,input_test,output_test);for i=1:particlesizeif objv(i)<personalbest_faval(i)personalbest_faval(i)=objv(i);%将第i个粒子作为个体最优解personalbest_x(i,:)=x(i,:);%更新最优解位置endend[globalbest_favalN,i]=min(personalbest_faval);globalbest_xn=personalbest_x(i,:);trace(1:N,k)=globalbest_xn;%每代最优x值trace(end,k)=globalbest_favalN;%%粒子更新for i=1:particlesizev(i,:)=w*v(i,:)+c1*rand*(personalbest_x(i,:)-x(i,:))+c2*rand*(globalbest_x-x(i,:));%rand会随机生成一个(0,1)的随机降低学习因子的比例for j=1:narvs%确定每个变量的速度,不超过最大速度if v(i,j)>vmaxv(i,j)=vmax;elseif v(i,j)<-vmaxv(i,j)=-vmax;endendx(i,:)=x(i,:)+v(i,:);endglobalbest_faval=globalbest_favalN;globalbest_x=globalbest_xn;k=k+1;
end
%%画图
figure(1);
plot(1:MaxNum,trace(end,:));
grid on;
xlabel('遗传代数');
ylabel('误差变化');
title('进化过程');
objfun.m
function [obj,T_sim]=objfun(X,input_train,output_train,input_test,output_test)
%%分别求解种群每个个体的目标值
%输入
%x:所有个体的初始权值与阈值
%input_train:训练样本输入
%output_train:训练样本输出
%hiddennum:隐藏神经元个数
%input_test:测试样本输入
%output_test:测试样本输出
%%输出
%obj:所有个体的预测样本的预测误差的范数,让这个误差最小,也就是每一个种群全都累加变成一个数,这里有10个种群,就是10个数
[M,N]=size(X);%返回一个M行N列的矩阵
obj=zeros(M,1);%所有个体误差初始化为M行1列也就是前面的粒子群规模,就是10行1列
T_sim=zeros(M,2000);%size(output_test,2)返回output_test的列数也就是2000个结果,也就是预测值是10行2000列的数值
for i=1:M[obj(i),T_sim(i,:)]=BpFunction(X(i,:),input_train,output_train,input_test,output_test);
end
T_sim=T_sim';
endBpFunction.m
%%输入
function [err,T_sim]=BpFunction(x,input_train,output_train,input_test,output_test)
inputnum=26;%输入层节点数量
hiddennum=12;%隐藏层节点数量
outputnum=1;%输出层节点数量
%%数据归一化
[inputn,inputps]=mapminmax(input_train,0,1);
[outputn,outputps]=mapminmax(output_train,0,1);%bp神经网络
net=newff(inputn,outputn,hiddennum);
%网络参数配置
net.trainParam.epochs=30;
net.trainParam.lr=0.001;
net.trainParam.goal=0.0001;
w1num=inputnum*hiddennum;%输入层到隐藏层的权值个数
w2num=outputnum*hiddennum;%输出层到隐藏层的权值个数
W1=x(1:w1num);
B1=x(w1num+1:w1num+hiddennum);
W2=x(w1num+hiddennum+1:w1num+hiddennum+w2num);
B2=x(w1num+hiddennum+w2num+1:w1num+hiddennum+w2num+outputnum);
net.iw{1,1}=reshape(W1,hiddennum,inputnum);
net.lw{2,1}=reshape(W2,outputnum,hiddennum);
net.b{1}=reshape(B1,hiddennum,1);
net.b{2}=reshape(B2,outputnum,1);
%%开始训练
%网络训练
net=train(net,inputn,outputn);
%%测试网络
t_sim=sim(net,input_test);
T_sim=mapminmax('reverse',t_sim,outputps);
err=norm(T_sim-output_test);
end3.结果
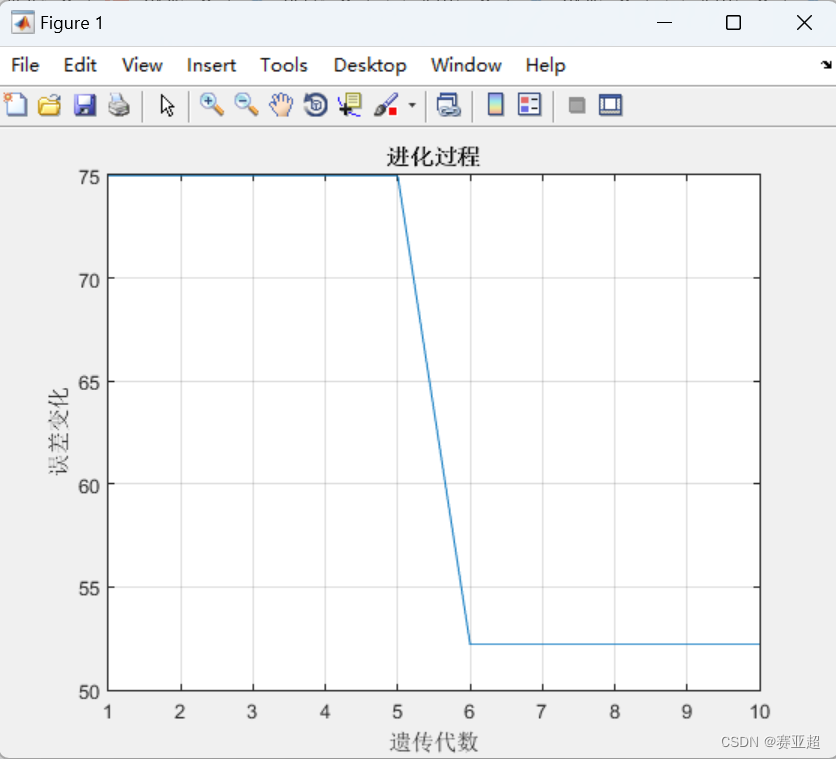
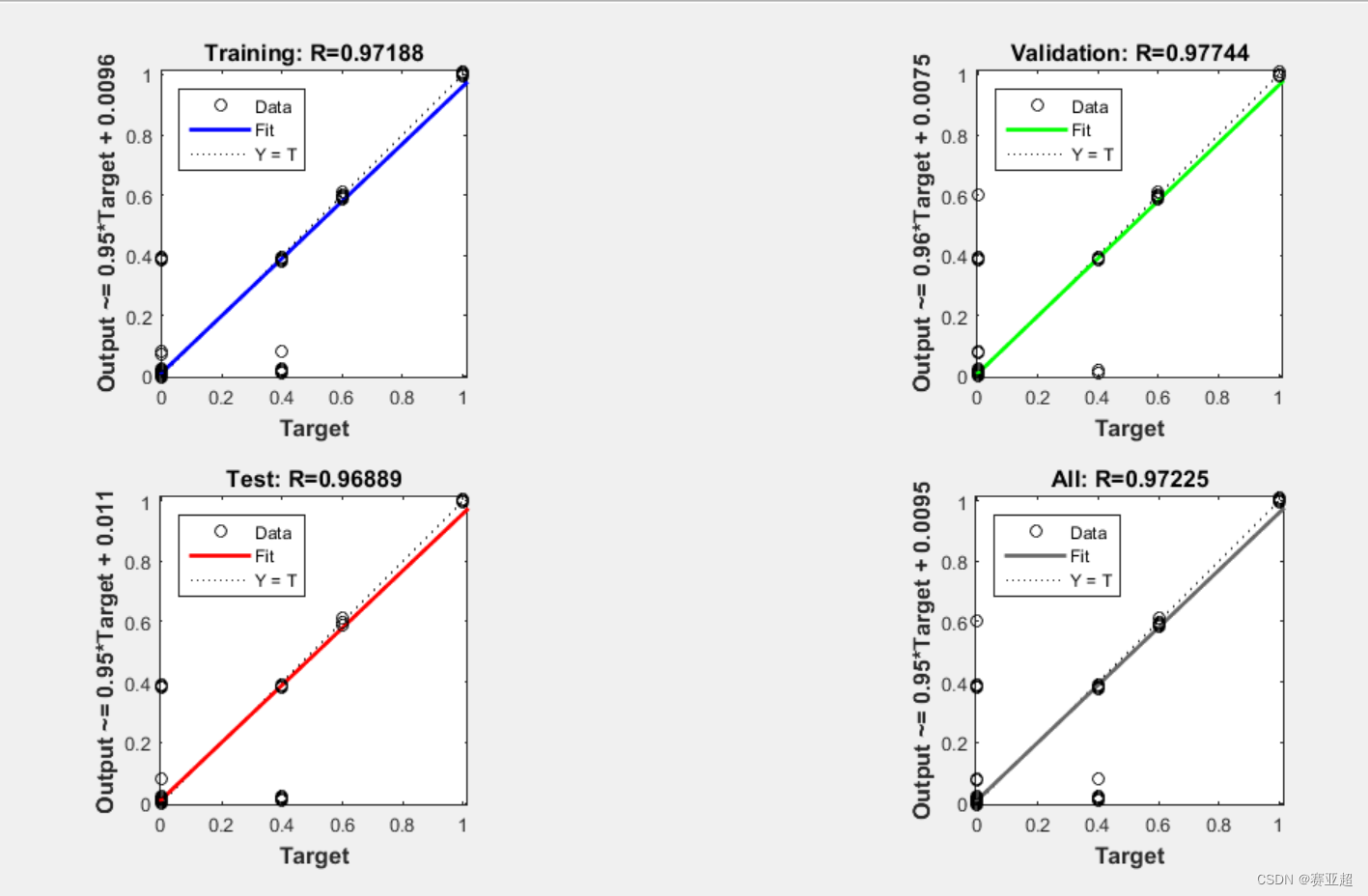
4.优化之前
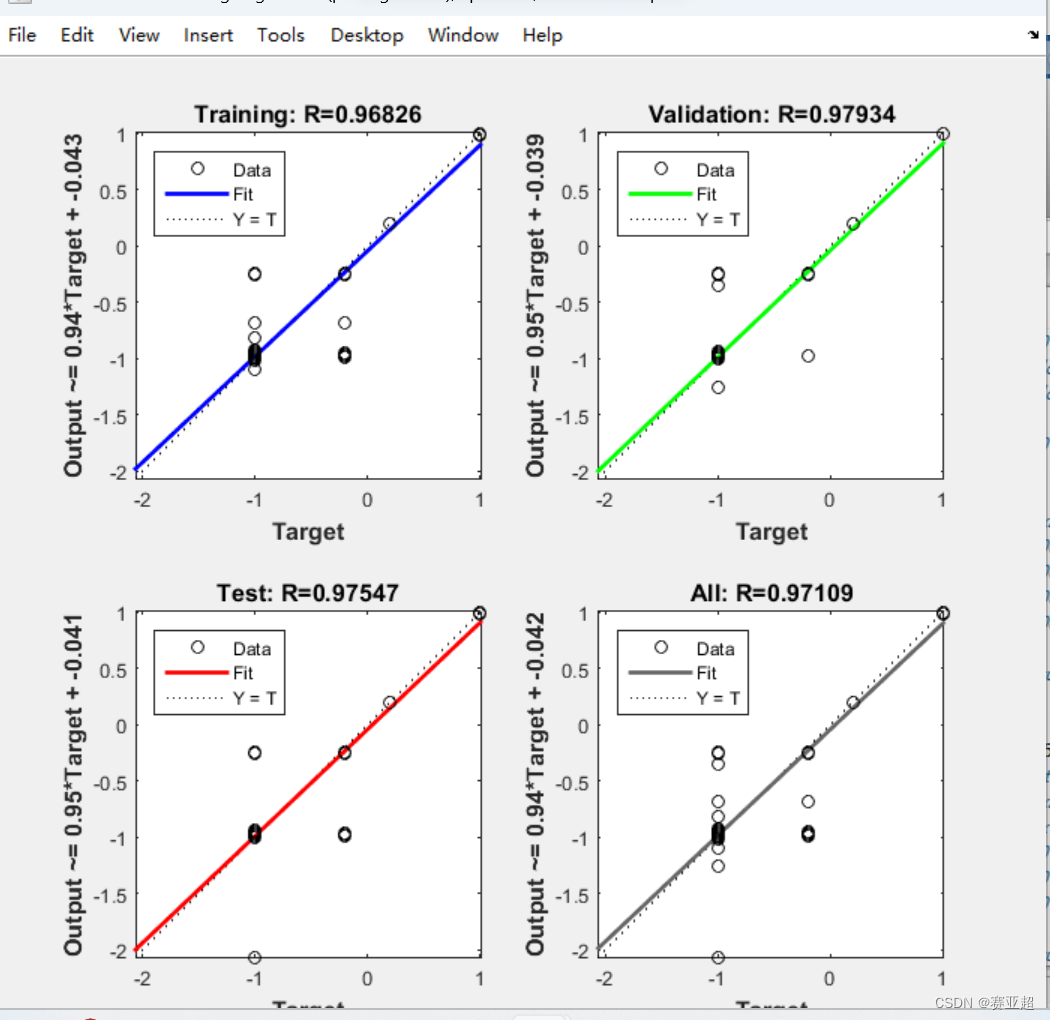
5.之所以上面有拟合差别大的地方在于bp网络自动将数据集中某一列全是一个数的给消去了,不知是系统消去的还是神经网络给消掉的。所以他会报错:
net.IW{1,1} must be a 12-by-8 matrix.
报这个错误的解决办法我是将某一列中第一行数据加个0.1。虽然是个解决办法,但是会影响到识别精度。所以不是个好办法。
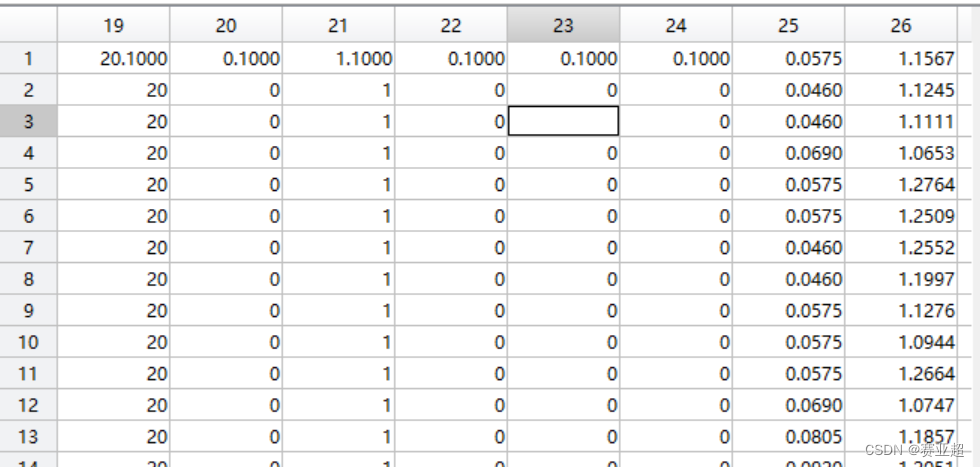
1.1粒子群算法基础
Pso算法是从随机解出发,通过迭代寻找最优解,通过适应度来评价解的品质,但是它比遗传算法规则更为简单,它没有遗传算法的“交叉”和“变异”操作,它是通过追随当前搜索到的最优值来寻找全局最优。
1.2基本原理
Pso算法起源对简单社会的模拟,具有很好的生物社会背景。Pso中每个优化问题的潜在解都是搜索空间的一只鸟,称之为粒子。所有的粒子都有一个由被优化的函数决定的适应值,每个粒子还有一个速度决定他们”飞行“的方向和距离。然后粒子就追随当前的最优粒子在解空间中搜索。设想这样一个场景:鸟群在森林中随机搜索食物,它们想要找到食物量最多的位置。但是所有的鸟都不知道食物具体在哪个位置,只能感受到食物大概在哪个方向。每只鸟沿着自己判定的方向进行搜索,并在搜索的过程中记录自己曾经找到过食物且量最多的位置,同时所有的鸟都共享自己每一次发现食物的位置以及食物的量,这样鸟群就知道当前在哪个位置食物的量最多。在搜索的过程中每只鸟都会根据自己记忆中食物量最多的位置和当前鸟群记录的食物量最多的位置调整自己接下来搜索的方向。鸟群经过一段时间的搜索后就可以找到森林中哪个位置的食物量最多(全局最优解)。
(1)PSO的基础:信息的社会共享
(2)粒子的两个属性:速度和位置(算法的两个核心要素)
速度表示粒子下一步迭代时移动的方向和距离,位置是所求解问题的一个解。
算法的6个重要参数
假设在D维搜索空间中,有N个粒子,每个粒子代表一个解,则:
① 第i个粒子的位置为:
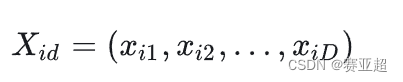
② 第 i个粒子的速度(粒子移动的距离和方向)为:
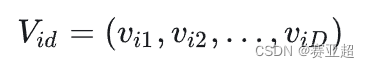
③ 第 i个粒子搜索到的最优位置(个体最优解)为:
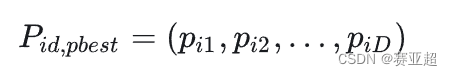
④ 群体搜索到的最优位置(群体最优解)为:
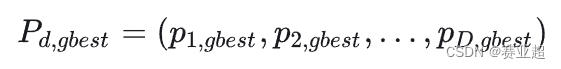
⑤ 第 i个粒子搜索到的最优位置的适应值(优化目标函数的值)为:
![]() ——个体历史最优适应值
——个体历史最优适应值
⑥ 群体搜索到的最优位置的适应值为:
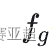 ——群体历史最优适应值
——群体历史最优适应值
1.3粒子群算法的流程图

1.4粒子群算法的伪代码

1.5速度更新公式
表述上叫速度,实际上就是粒子下一步迭代移动的距离和方向,也就是一个位置向量。
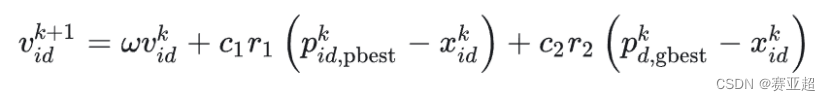
(1)速度更新公式的解释
① 第一项:惯性部分
由惯性权重和粒子自身速度构成,表示粒子对先前自身运动状态的信任。
② 第二项:认知部分
表示粒子本身的思考,即粒子自己经验的部分,可理解为粒子当前位置与自身历史最优位置之间的距离和方向。
③ 第三项:社会部分
表示粒子之间的信息共享与合作,即来源于群体中其他优秀粒子的经验,可理解为粒子当前位置与群体历史最优位置之间的距离和方向。
(2)速度更新公式的参数定义

(3)速度的方向
粒子下一步迭代的移动方向 = 惯性方向 + 个体最优方向 + 群体最优方向
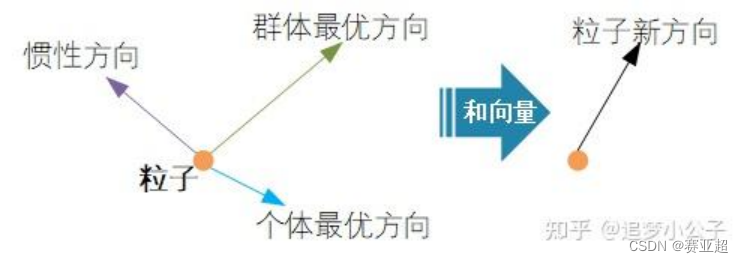
1.6、位置更新公式
上一步的位置 + 下一步的速度
1.7算法参数的详细解释
- 粒子群规模: N
一个正整数,推荐取值范围:[20,1000],简单问题一般取20~40,较难或特定类别的问题可以取100~200。较小的种群规模容易陷入局部最优;较大的种群规模可以提高收敛性,更快找到全局最优解,但是相应地每次迭代的计算量也会增大;当种群规模增大至一定水平时,再增大将不再有显著的作用。
(2)粒子维度: D
粒子搜索的空间维数即为自变量的个数。
(3)迭代次数: K
推荐取值范围:[50,100],典型取值:60、70、100;这需要在优化的过程中根据实际情况进行调整,迭代次数太小的话解不稳定,太大的话非常耗时,没有必要。
(4)惯性权重:w
1998年,Yuhui Shi和Russell Eberhart对基本粒子群算法引入了惯性权重(inertia weight)w,并提出动态调整惯性权重以平衡收敛的全局性和收敛速度,该算法被称为标准PSO算法。
参数意义
惯性权重w表示上一代粒子的速度对当代粒子的速度的影响,或者说粒子对当前自身运动状态的信任程度,粒子依据自身的速度进行惯性运动。惯性权重使粒子保持运动的惯性和搜索扩展空间的趋势。w值越大,探索新区域的能力越强,全局寻优能力越强,但是局部寻优能力越弱。反之,全局寻优能力越弱,局部寻优能力强。较大的w有利于全局搜索,跳出局部极值,不至于陷入局部最优;而较小的w有利于局部搜索,让算法快速收敛到最优解。当问题空间较大时,为了在搜索速度和搜索精度之间达到平衡,通常做法是使算法在前期有较高的全局搜索能力以得到合适的种子,而在后期有较高的局部搜索能力以提高收敛精度,所以w不宜为一个固定的常数[3]。
当w=1时,退化成基本粒子群算法,当 w=0 时,失去对粒子本身经验的思考。推荐取值范围:[0.4,2],典型取值:0.9、1.2、1.5、1.8
改善惯性权重w
在解决实际优化问题时,往往希望先采用全局搜索,使搜索空间快速收敛于某一区域,然后采用局部精细搜索以获得高精度的解。因此提出了自适应调整的策略,即随着迭代的进行,线性地减小w的值。这里提供一个简单常用的方法——线性变化策略:随着迭代次数的增加,惯性权重w不断减小,从而使得粒子群算法在初期具有较强的全局收敛能力,在后期具有较强的局部收敛能力。
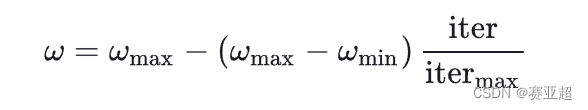

(5)学习因子: c1,c2
也称为加速系数或加速因子(这两个称呼更加形象地表达了这两个系数的作用)
c1 表示粒子下一步动作来源于自身经验部分所占的权重,将粒子推向个体最优位置
![]()
的加速权重;
c2表示粒子下一步动作来源于其它粒子经验部分所占的权重,将粒子推向群体最优位置
![]()
的加速权重;
c1=0:无私型粒子群算法,"只有社会,没有自我",迅速丧失群体多样性,易陷入局部最优而无法跳出;
c2=0:自我认知型粒子群算法,"只有自我,没有社会",完全没有信息的社会共享,导致算法收敛速度缓慢;
c1,c2都不为0:完全型粒子群算法,更容易保持收敛速度和搜索效果的均衡,是较好的选择。
低的值使粒子在目标区域外徘徊,而高的值导致粒子越过目标区域。 推荐取值范围:[0,4];典型取值:c1=c2=2、c1=1.6和 c2=1.8 、c1=1.6和 c2=2 ,针对不同的问题有不同的取值,一般通过在一个区间内试凑来调整这两个值。
1.8算法的一些重要概念和技巧
(1)适应值(fitness values)
即优化目标函数的值,用来评价粒子位置的好坏程度,决定是否更新粒子个体的历史最优位置和群体的历史最优位置,保证粒子朝着最优解的方向搜索。
(2)位置限制
限制粒子搜索的空间,即自变量的取值范围,对于无约束问题此处可以省略。
(3)速度限制
为了平衡算法的探索能力与开发能力,需要设定一个合理的速度范围,限制粒子的最大速度 vmax ,即粒子下一步迭代可以移动的最大距离。
1.9代码
clcclearclose allE=0.000001;maxnum=800;%最大迭代次数narvs=2;%目标函数的自变量个数particlesize=50;%粒子群规模c1=2;%每个粒子的个体学习因子,加速度常数c2=2;%每个粒子的社会学习因子,加速度常数w=0.6;%惯性因子vmax=5;%粒子的最大飞翔速度v=2*rand(particlesize,narvs);%粒子飞翔速度x=-300+600*rand(particlesize,narvs);%粒子所在位置%定义适应度函数fitness=inline('(x(1)^2+x(2)^2)/10000','x');for i=1:particlesizef(i)=fitness(x(i,:));endpersonalbest_x=x;personalbest_faval=f;[globalbest_faval,i]=min(personalbest_faval);globalbest_x=personalbest_x(i,:);k=1;while (k<=maxnum)for i=1:particlesizef(i)=fitness(x(i,:));if f(i)<personalbest_faval(i)personalbest_faval(i)=f(i);personalbest_x(i,:)=x(i,:);endend[globalbest_faval,i]=min(personalbest_faval);globalbest_x=personalbest_x(i,:);for i=1:particlesizev(i,:)=w*v(i,:)+c1*rand*(personalbest_x(i,:)-x(i,:))...+c2*rand*(globalbest_x-x(i,:));for j=1:narvsif v(i,j)>vmaxv(i,j)=vmax;elseif v(i,j)<-vmaxv(i,j)=-vmax;endendx(i,:)=x(i,:)+v(i,:);endff(k)=globalbest_faval;if globalbest_faval<Ebreakend% figure(1)% for i= 1:particlesize% plot(x(i,1),x(i,2),'*')% endk=k+1;endxbest=globalbest_x;figure(2)set(gcf,'color','white');plot(1:length(ff),ff)相关文章:
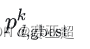
粒子群优化pso结合bp神经网络优化对csv文件预测matlab(3)
1.csv数据为密西西比数据集,获取数据集可以管我要,数据集内容形式如下图: 2.代码 这里参考的是b站的一位博主。 数据集导入教程在我的另一篇文章bp写过,需要的话可以去看一下 psobp.m close all clc%读取数据 inputX; outputY;…...

软性演员-评论家算法 SAC
软性演员-评论家算法 SAC 软性演员-评论家算法 SAC优势原理软性选择模型结构目标函数重参数化熵正则化代码实现 软性演员-评论家算法 SAC 优势原理 DDPG 的问题在于,训练不稳定、收敛差、依赖超参数、不适应复杂环境。 软性演员-评论家算法 SAC,更稳定…...

Nginx多域名部署多站点
目录 1.修改配置文件nginx.conf 2. 修改hosts文件 1.修改配置文件nginx.conf 在配置文件的 server_name 处修改成自己需要的域名,然后保存退出 j 查看语法是否错误,然后重启nginx nginx -t # 查看语法是否正确 systemctl restart nginx # 重启nginx …...

Java的常规面试题
Java的面试题主要涉及Java基础知识、并发编程、集合原理、JVM原理、I/O与网络编程、设计模式、互联网常用框架等多个领域[6]。一些常见的面试问题包括: 1. 面向对象的特征:继承、封装和多态性。 2. 访问修饰符public、private、protected以及默认时的区别…...

大数据技术发展史
文章目录 Google论文HadoopHive大数据生态 Google论文 今天我们常说的大数据技术,其实起源于Google在2004年前后发表的三篇论文,也就是我们经常听到的“三驾马车”,分别是分布式文件系统GFS、大数据分布式计算框架MapReduce和NoSQL数据库系统…...

linux常见基础指令
入门常见基础指令 ls、stat、 pwd 、cd、tree、 whoami、 touch、 mkdir、 rm 、 man、 cp、mv、cat、tac、echo、>、 >>、 < 、more、 less、 head、 tail、date、 cal、 find、 which、alias、whereis、grep、zip与unzip、 tar、bc、uname、xargs... 热键Tab、…...

“人家赚那么多”系列01:如何练习?练什么?
01 如何练习?练习什么? 今年计划重点围绕「在不骗自己的前提下,如何才能把事儿彻底做好,并做得有声有色?」为主题来写点儿东西,聊聊我是怎么做的,如何通过一些有效的方法来不断优化自己的。 想把…...

【Android】使用android studio查看内置数据库信息
要使用Android Studio查看内置数据库信息,可以按照以下步骤进行操作: 打开Android Studio并打开你的项目。 在左侧的Project窗口中,找到并展开你的app模块。 找到并展开"app" > "src" > "main"文件夹。…...

PHP开发日志 ━━ 基于PHP和JS的AES相互加密解密方法详解(CryptoJS) 适合CryptoJS4.0和PHP8.0
最近客户在做安全等保,需要后台登录密码采用加密方式,原来用个base64变形一下就算了,现在不行,一定要加密加key加盐~~ 前端使用Cypto-JS加密,传输给后端使用PHP解密,当然,前端虽然有key有盐&…...

2021-01-03 excel实现列递增,行保持不变
需求:excel文档数据操作的时候发现自动递增只能实现列不变行号递增 我这里里需要的是列递增行不变 解决方式:通过一些函数的组合使用 INDIRECT("驻场明细!"&CHAR(ROW()62)&ROW(驻场明细!A$28)) INDIRECT()函数的使用: INDI…...

[Python]两个杯子取水问题
利用两个杯子巧取三升水: 今天的这个趣味数学小游戏是利用两个没有刻度的水杯,巧妙地取出三升水来。 题目的条件是:一个总容量为6升的杯子和一个总容量为5升的杯子,同时面前有无限容量的水供你使用。不借助其它任何的容器…...

C++汇编语言学习计划
前几天买了某游戏的外挂,感觉外挂在我计算机上进行了不少操作,我想一探究竟,可是只有exe,没办法,翻译成汇编我也看不懂,索性来简单学习下。访问Chatgpt4,给了如下学习计划。 要从零开始学习C生成…...
微信服务号升级订阅号条件
服务号和订阅号有什么区别?服务号转为订阅号有哪些作用?首先我们要看一下服务号和订阅号的主要区别。1、服务号推送的消息没有折叠,消息出现在聊天列表中,会像收到消息一样有提醒。而订阅号推送的消息是折叠的,“订阅号…...
SpringBoot整合mybatis多数据源
废话不多说先上结果 对应数据库 首先导入所需的mybatis、mysql和lombok依赖 <dependency><groupId>org.mybatis.spring.boot</groupId><artifactId>mybatis-spring-boot-starter</artifactId><version>2.2.2</version></dependen…...
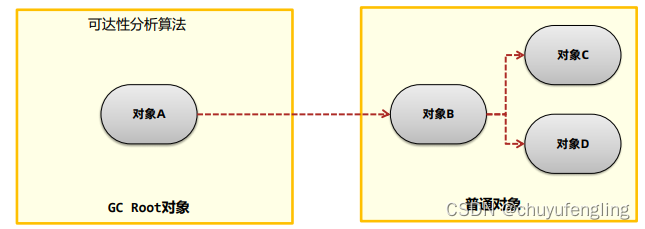
垃圾收集器与内存分配策略
内存分配和回收原则 对象优先在Eden区分配 大对象直接进入老年代 长期存活的对象进入老年代 什么是内存泄漏 不再使用的对象在系统中未被回收,内存泄漏的积累可能会导致内存溢出 自动垃圾回收与手动垃圾回收 自动垃圾回收:由虚拟机来自动回收对象…...

Python计算三角形的面积
Python 计算三角形的面积 以下实例为通过用户输入三角形三边长度,并计算三角形的面积: # 三角形第一边长 a 3 # 三角形第二边长 b 4 c float( input("输入三角形第三边长: ") ) # 计算半周长 s (a b c) / 2 # 计算…...
】万能字符单词拼写(JavaPythonC++JS实现))
198.【2023年华为OD机试真题(C卷)】万能字符单词拼写(JavaPythonC++JS实现)
🚀点击这里可直接跳转到本专栏,可查阅顶置最新的华为OD机试宝典~ 本专栏所有题目均包含优质解题思路,高质量解题代码(Java&Python&C++&JS分别实现),详细代码讲解,助你深入学习,深度掌握! 文章目录 一. 题目-万能字符单词拼写二.解题思路三.题解代码Pytho…...

Tomcat服务为什么起不来?
转载说明:如果您喜欢这篇文章并打算转载它,请私信作者取得授权。感谢您喜爱本文,请文明转载,谢谢。 服务跑在Tomcat下面,有时候会遇到Tomcat起不来的情况。目前为止常遇到的情况有如下几种: 1. Tomcat服务…...
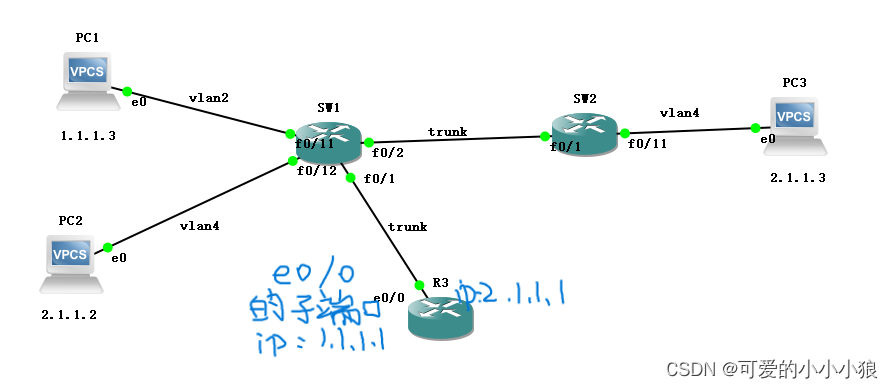
计算机网络 VLAN
路由器将多个局域网连接起来,而交换机将一个局域网里的设备连接起来。 路由器的端口分配局域网的网段(子网网段),局域网的内部设备的ip都在这个网段里,再由交换机将数据派发到目的设备,交换机是按照MAC地址…...
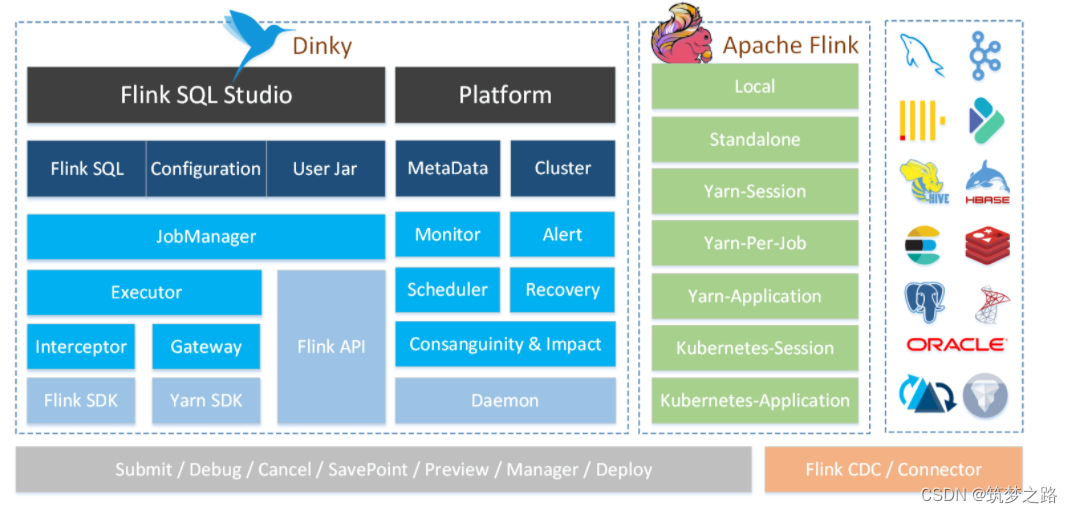
docker搭建Dinky —— 筑梦之路
简介 Dinky 是一个 开箱即用 、易扩展 ,以 Apache Flink 为基础,连接 OLAP 和 数据湖 等众多框架的 一站式 实时计算平台,致力于 流批一体 和 湖仓一体 的探索与实践。 主要功能 其主要功能如下: 沉浸式 FlinkSQL 数据开发&#x…...

Linux 文件类型,目录与路径,文件与目录管理
文件类型 后面的字符表示文件类型标志 普通文件:-(纯文本文件,二进制文件,数据格式文件) 如文本文件、图片、程序文件等。 目录文件:d(directory) 用来存放其他文件或子目录。 设备…...

前端倒计时误差!
提示:记录工作中遇到的需求及解决办法 文章目录 前言一、误差从何而来?二、五大解决方案1. 动态校准法(基础版)2. Web Worker 计时3. 服务器时间同步4. Performance API 高精度计时5. 页面可见性API优化三、生产环境最佳实践四、终极解决方案架构前言 前几天听说公司某个项…...

【网络安全产品大调研系列】2. 体验漏洞扫描
前言 2023 年漏洞扫描服务市场规模预计为 3.06(十亿美元)。漏洞扫描服务市场行业预计将从 2024 年的 3.48(十亿美元)增长到 2032 年的 9.54(十亿美元)。预测期内漏洞扫描服务市场 CAGR(增长率&…...

【Go】3、Go语言进阶与依赖管理
前言 本系列文章参考自稀土掘金上的 【字节内部课】公开课,做自我学习总结整理。 Go语言并发编程 Go语言原生支持并发编程,它的核心机制是 Goroutine 协程、Channel 通道,并基于CSP(Communicating Sequential Processes࿰…...

视频字幕质量评估的大规模细粒度基准
大家读完觉得有帮助记得关注和点赞!!! 摘要 视频字幕在文本到视频生成任务中起着至关重要的作用,因为它们的质量直接影响所生成视频的语义连贯性和视觉保真度。尽管大型视觉-语言模型(VLMs)在字幕生成方面…...

数据链路层的主要功能是什么
数据链路层(OSI模型第2层)的核心功能是在相邻网络节点(如交换机、主机)间提供可靠的数据帧传输服务,主要职责包括: 🔑 核心功能详解: 帧封装与解封装 封装: 将网络层下发…...
)
C#学习第29天:表达式树(Expression Trees)
目录 什么是表达式树? 核心概念 1.表达式树的构建 2. 表达式树与Lambda表达式 3.解析和访问表达式树 4.动态条件查询 表达式树的优势 1.动态构建查询 2.LINQ 提供程序支持: 3.性能优化 4.元数据处理 5.代码转换和重写 适用场景 代码复杂性…...

Chromium 136 编译指南 Windows篇:depot_tools 配置与源码获取(二)
引言 工欲善其事,必先利其器。在完成了 Visual Studio 2022 和 Windows SDK 的安装后,我们即将接触到 Chromium 开发生态中最核心的工具——depot_tools。这个由 Google 精心打造的工具集,就像是连接开发者与 Chromium 庞大代码库的智能桥梁…...

Spring AOP代理对象生成原理
代理对象生成的关键类是【AnnotationAwareAspectJAutoProxyCreator】,这个类继承了【BeanPostProcessor】是一个后置处理器 在bean对象生命周期中初始化时执行【org.springframework.beans.factory.config.BeanPostProcessor#postProcessAfterInitialization】方法时…...

使用homeassistant 插件将tasmota 接入到米家
我写一个一个 将本地tasmoat的的设备同通过ha集成到小爱同学的功能,利用了巴法接入小爱的功能,将本地mqtt转发给巴法以实现小爱控制的功能,前提条件。1需要tasmota 设备, 2.在本地搭建了mqtt服务可, 3.搭建了ha 4.在h…...