【蓝桥杯集训·每日一题】AcWing 3696. 构造有向无环图
文章目录
- 一、题目
- 1、原题链接
- 2、题目描述
- 二、解题报告
- 1、思路分析
- 2、时间复杂度
- 3、代码详解
- 三、知识风暴
- 拓扑排序
一、题目
1、原题链接
3696. 构造有向无环图
2、题目描述
给定一个由 n 个点和 m 条边构成的图。
不保证给定的图是连通的。
图中的一部分边的方向已经确定,你不能改变它们的方向。
剩下的边还未确定方向,你需要为每一条还未确定方向的边指定方向。
你需要保证在确定所有边的方向后,生成的图是一个有向无环图(即所有边都是有向的且没有有向环的图)。
输入格式
第一行包含整数 T,表示共有 T 组测试数据。
每组数据第一行包含两个整数 n,m。
接下来 m 行,每行包含三个整数 t,x,y,用来描述一条边的信息,其中 t 表示边的状态,如果 t=0,则表示边是无向边,如果
t=1,则表示边是有向边。x,y 表示这条边连接的两个端点,如果是有向边则边的方向是从 x 指向 y。保证图中没有重边(给定了 (x,y),就不会再次出现 (x,y) 或出现 (y,x) 和自环(不会出现 x=y 的情况)。
输出格式
对于每组数据,如果无法构造出有向无环图,则输出一行
NO。否则,先输出一行
YES,随后 m 行,每行包含两个整数 x,y,用来描述最终构造成的有向无环图中的每条边的具体方向(x 指向
y),边的先后顺序随意。注意,已经确定方向的边,不能更改方向。
如果答案不唯一,输出任意合理方案均可。
数据范围
对于前三个测试点,1≤n,m≤10。
对于全部测试点,1≤T≤20000,2≤n≤2×105,1≤m≤min(2×105,n(n−1)/2),0≤t≤1,1≤x,y≤n。
保证在一个测试点中,所有 n 的和不超过 2×105,所有 m 的和不超过 2×105。输入样例:
4 3 1 0 1 3 5 5 0 2 1 1 1 5 1 5 4 0 5 2 1 3 5 4 5 1 1 2 0 4 3 1 3 1 0 2 3 1 2 4 4 5 1 4 1 1 1 3 0 1 2 1 2 4 1 3 2输出样例:
YES 3 1 YES 2 1 1 5 5 4 2 5 3 5 YES 1 2 3 4 3 1 3 2 2 4 NO
二、解题报告
1、思路分析
思路来源:y总yyds
y总yyds
(1)如果给定图中存在回路(即无法构成构成拓扑序列)则无论怎样为无向边添加方向,都不可能无环,所以此时无解。
(2)如果给定的图中不存在回路(即存在拓扑序列),则可以将与无向边相连的点,在拓扑序列中前面的点指向后面的点,这样为每条边添加方向,不会存在环。
(3)按上述模拟,先输出所有有向边,然后再按(2)输出所有无向边(同时为无向边添加方向)。
2、时间复杂度
拓扑排序时间复杂度为O(n+m)(n为点数,m为边数)
3、代码详解
/*注:使用cin、cout最后一个测试数据会超时*/
#include <iostream>
#include <queue>
#include <cstring>
#include <algorithm>
using namespace std;
const int N=200010,M=N; //N代表点数,M代表边数
//邻接表存储有向边
int h[N],e[M],ne[M],idx; //h[]存储每个点的第一条边的idx,e[]存储每条边的终点,ne[]存储每个点同起点下一条边的idx,idx为边的编号
int d[N]; //记录每个点的入度
int ans[N]; //记录拓扑序列
int pos[N]; //记录每个点在拓扑排序中的位置
int n,m,T;
//存储无向边
struct Edge{int a,b;
}edge[M];
//邻接表中添加一条边
void add(int a,int b){e[idx]=b;ne[idx]=h[a];h[a]=idx++;
}
//拓扑排序
bool tp(){queue<int> q;int ord=0,num=0; //ord记录每个点入队顺序,也就是在拓扑序列中的先后顺序for(int i=1;i<=n;i++){if(d[i]==0) q.push(i),pos[i]=++ord;}while(!q.empty()){int t=q.front();q.pop();ans[num++]=t;for(int i=h[t];i!=-1;i=ne[i]){int j=e[i];d[j]--;if(d[j]==0) q.push(j),pos[j]=++ord;}}return num==n;
}
int main(){cin>>T;while(T--){memset(h,-1,sizeof h);memset(d,0,sizeof d);idx=0;scanf("%d%d",&n,&m);int t,x,y;int cnt=0;while(m--){scanf("%d%d%d",&t,&x,&y);if(t==0) edge[cnt++]={x,y};else{add(x,y);d[y]++;}}if(!tp()) puts("NO");else{puts("YES");//先输出所有有向边for(int i=1;i<=n;i++){for(int j=h[i];j!=-1;j=ne[j]){printf("%d %d\n",i,e[j]);}}//输出无向边的同时给边“确定方向”for(int i=0;i<cnt;i++){int x=edge[i].a,y=edge[i].b;if(pos[x]>pos[y]) swap(x,y); //拓扑序列中前面的点指向后面的点printf("%d %d\n",x,y);}}}return 0;
}
三、知识风暴
拓扑排序
- 拓扑序列满足:如果存在vi到vj的路径,则顶点vi必然在顶点vj之前。
- 拓扑排序过程:
- 从有向图中选择一个没有前驱(即入度为0)的点并且输出。
- 从图中删去该顶点,并且删去从该顶点发出的全部有向边。
- 重复上述两步,直到剩余的图中不再存在没有前驱的顶点为止。
相关文章:

【蓝桥杯集训·每日一题】AcWing 3696. 构造有向无环图
文章目录一、题目1、原题链接2、题目描述二、解题报告1、思路分析2、时间复杂度3、代码详解三、知识风暴拓扑排序一、题目 1、原题链接 3696. 构造有向无环图 2、题目描述 给定一个由 n 个点和 m 条边构成的图。 不保证给定的图是连通的。 图中的一部分边的方向已经确定&#…...
国内vs国外:外贸建站该如何选择?
外贸建站找国内还是国外? 答案是:国内。 随着互联网的发展,越来越多的企业开始意识到在网络上进行商业活动的重要性。 其中,建立一个专业的外贸网站是企业在国际市场上拓展业务的关键。 然而,对于选择国内还是国外…...

HLS协议有哪些特别优势
阿酷TONY / 2023-3-3 / 长沙 可以实现码率的动态自适应,清晰度动态成为可能;HLS是基于HTTP 协议的,更易于做各平台的适配与兼容;多终端跨平台的支持性: PC端, Android端, IOS 平台,微信之类的都支持&am…...

JavaScript里的回调函数属于闭包吗?
回调函数本身不一定属于闭包,但是在某些情况下,它们可能会涉及闭包。 回调函数通常是指在异步操作完成时执行的函数。它们在 JavaScript 中被广泛使用,例如在处理 AJAX 请求、定时器、事件处理程序等方面。 在使用回调函数时,如…...
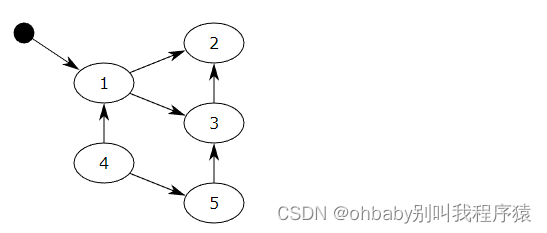
编程基本概念
程序的构成 python程序由模块组成,一个模块对应一个python源文件,后缀为.py模块由语句组成,运行python程序时,按照模块中的语句顺序依次执行语句是python程序的构造单元,用于创建对象,变量赋值,…...
Azure OpenAI 官方指南02|ChatGPT 的架构设计与应用实例
ChatGPT 作为即将在微软全球 Azure 公有云平台正式发布的服务,已经迅速成为了众多用户关心的服务之一。而由 OpenAI 发布的 ChatGPT 产品,仅仅上线两个月,就成为互联网历史上最快突破一亿月活的应用。本期从技术角度深度解析 ChatGPT 的架构设…...
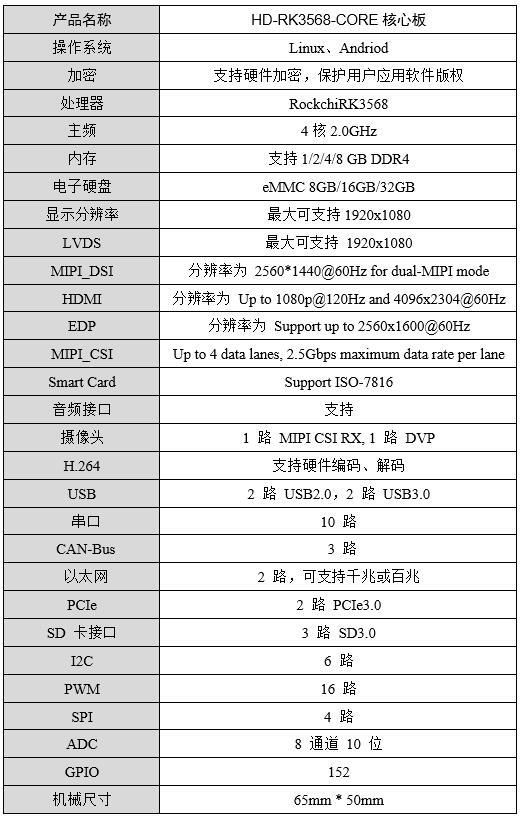
RK3568核心板以太网大数据测试报告-万象奥科
1. 测试对象HD-RK3568-IOT 底板基于HD-RK3568-CORE工业级核心板设计(双网口、双CAN、5路串口),接口丰富,适用于工业现场应用需求,亦方便用户评估核心板及CPU的性能。适用于工业自动化控制、人机界面、中小型医疗分析器…...

来 CSDN 三年,我写了一本Python书
大家好,我是朱小五。转眼间已经来 CSDN 3年了,其中给大家一共分享了252篇Python文章。 但这三年,最大的收获还是写了一本Python书! 在这个自动化时代,我们有很多重复无聊的工作要做。想想这些你不再需要一次又一次地做…...
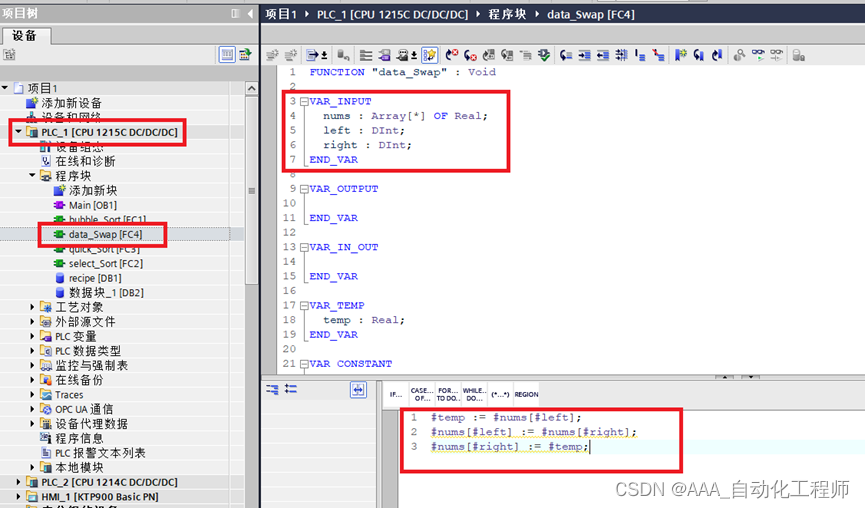
TIA博途中通过SCL语言实现快速排序的具体方法示例
TIA博途中通过SCL语言实现快速排序的具体方法示例 首先,了解一下快速排序的原理: 排序算法的思想非常简单,在待排序的数列中,我们首先要找一个数字作为基准数。为了方便,我们一般选择第 1 个数字作为基准数(其实选择第几个并没有关系)。接下来我们需要将这个待排序的数列…...

第 46 届世界技能大赛浙江省选拔赛“网络安全“项目B模块任务书
第46届世界技能大赛浙江省选拔赛"网络安全"项目B模块(网络安全事件响应、数字取证调查)第46届世界技能大赛浙江省选拔赛"网络安全"项目B模块2.1 第一部分 事件响应2.2 第二部分 数字取证调查2.3 第三部分 应用程序安全第46届世界技能…...

【C】字符串操作函数
初始化字符串 #include <string.h>void *memset(void *s, int c, size_t n); 返回值:s指向哪,返回的指针就指向哪memset函数把s所指的内存地址开始的n个字节都填充为c的值。通常c的值为0,把一块内存区清零。例如定义char buf[10];&…...

【python】 pytest自动化测试框架--selenium,requests,appium自动化工具
一、pytest简介 pytest是python的一种单元测试框架,与python自带的unittest测试框架类似,但是比unittest框架使用起来更简洁,效率更高 二、 pytest 单元测试框架 1、pytest 特点 pytest是python当中的一个单元框架,比unittest更灵…...
Spring boot 实战指南(三):配置事务,整合Elasticsearch、swagger、redis、rabbitMQ
文章目录一、配置事务依赖使用注解二、Elasticsearch创建项目配置maven完善依赖es连接配置实体映射repositoryservicecontroller三、swagger依赖启动类路径匹配配置配置类controller注解四、redis(代码实现)依赖yml配置配置类封装redisTamplate五、rabbi…...
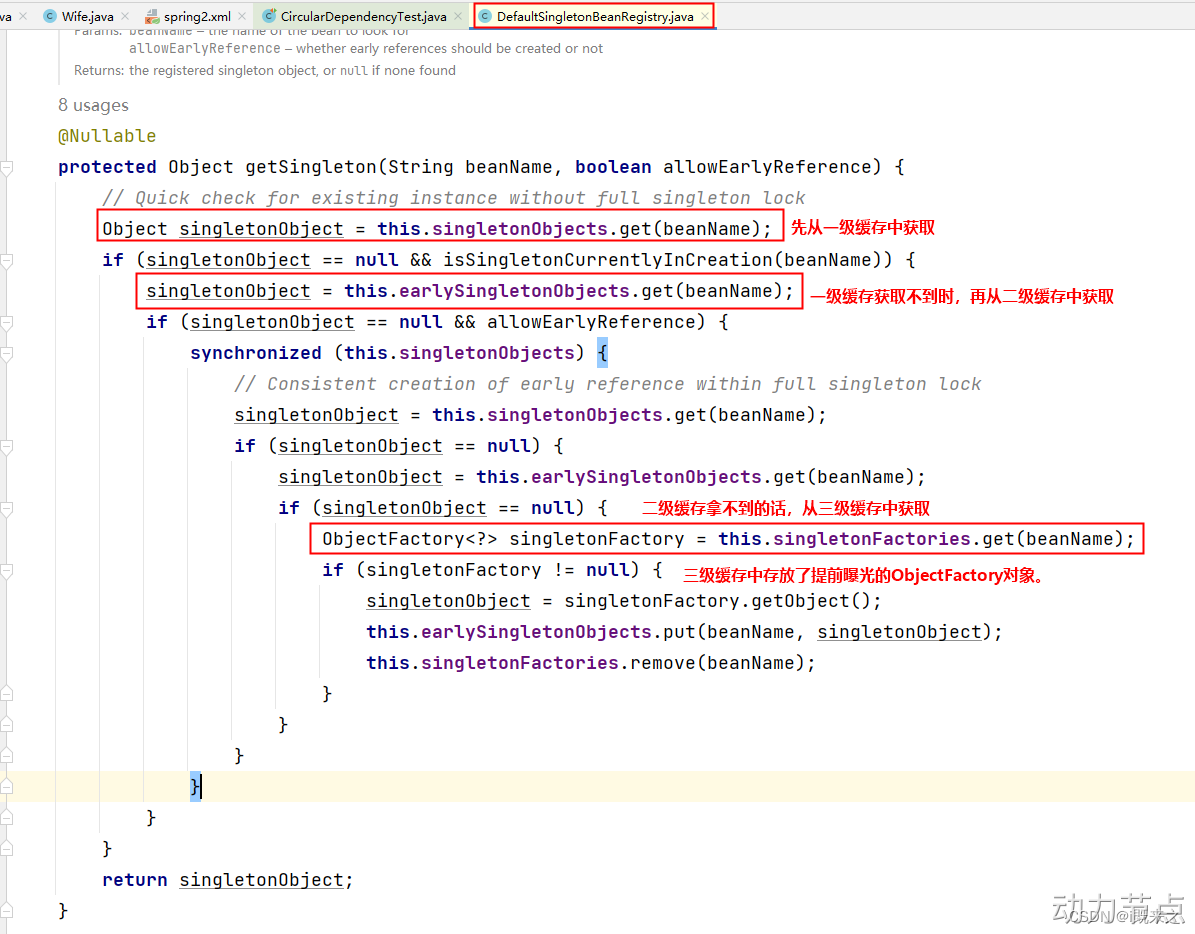
九、Bean的循环依赖问题
1 什么是Bean的循环依赖 A对象中有B属性。B对象中有A属性。这就是循环依赖。我依赖你,你也依赖我。 比如:丈夫类Husband,妻子类Wife。Husband中有Wife的引用。Wife中有Husband的引用。 2 singleton下的set注入产生的循环依赖 丈夫类 pac…...

macOS关闭SIP后,仍无法修改/usr文件夹下文件
发现问题 MacOS 升级到Big Sur后,删除多余的python3文件,发现写不到磁盘,会报OSError: [Errno 30] Read-only file system的错误。经过了解,在Mac OS10.11 之后,苹果公司为了提高系统环境安全,引入了一个内…...
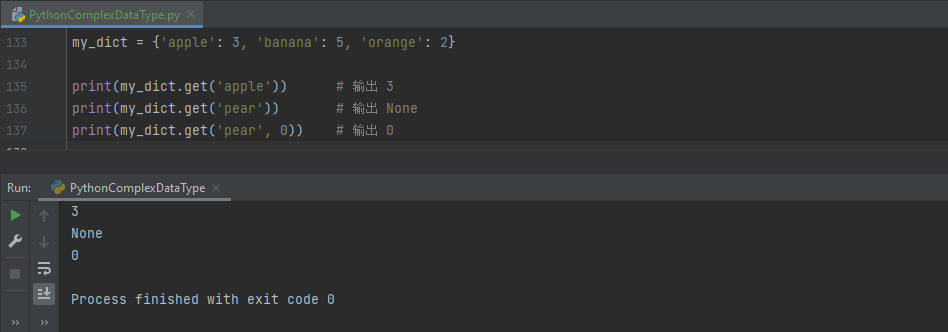
【编程基础之Python】8、Python复合数据类型
【编程基础之Python】8、Python复合数据类型Python复合数据类型列表(List)创建列表访问元素内置方法列表操作元组(Tuple)创建元组访问元素集合(Set)创建集合基本操作其他操作字典(Dictionary&am…...
自动驾驶决策规划-控制方向学习资料总结(附相关资料的链接)
项目仓库 欢迎访问我的Github主页 项目名称说明chhCpp学习C仓库chhRobotics学习自动驾驶、控制理论相关仓库(python实现)chhRobotics_CPP学习自动驾驶、控制理论相关仓库(c实现)chhML 、chh-MachineLearning学习机器学习仓库chhRL学习强化学习仓库chhTricks存放一些有意思的t…...

网络安全岗位介绍——售前工程师
一、工作内容 1、独立完成并配合销售人员引导客户完成方案设计、产品选型、配置报价和能为客户提供安全咨询与方案优化等服务; 2、作为售前工程师,跟踪整个项目的进展,和销售进行配合,协调公司各种资源完成项目中标; 3、编写投标文件的技术…...

nodejs安装和卸载超详细步骤
安装程序①下载完成后,双击安装包,开始安装,使用默认配置安装一直点next即可,安装路径默认在C:\Program Files下,也可以自定义修改②安装路径默认在C:\Program Files下面,也能够自定义修改,而后…...

【Leetcode】移除链表元素 链表的中间节点 链表中倒数第k个节点
目录 一.【Leetcode203】移除链表元素 1.链接 2.题目再现 A.双指针法 B.类尾删法 C.哨兵位 二.【Leetcode876】链表的中间节点 1.链接:链表的中间节点 2.题目再现 3.解法:快慢指针 三.链表中倒数第k个节点 1.链接:链表中倒数第k个…...

从WWDC看苹果产品发展的规律
WWDC 是苹果公司一年一度面向全球开发者的盛会,其主题演讲展现了苹果在产品设计、技术路线、用户体验和生态系统构建上的核心理念与演进脉络。我们借助 ChatGPT Deep Research 工具,对过去十年 WWDC 主题演讲内容进行了系统化分析,形成了这份…...

【论文阅读28】-CNN-BiLSTM-Attention-(2024)
本文把滑坡位移序列拆开、筛优质因子,再用 CNN-BiLSTM-Attention 来动态预测每个子序列,最后重构出总位移,预测效果超越传统模型。 文章目录 1 引言2 方法2.1 位移时间序列加性模型2.2 变分模态分解 (VMD) 具体步骤2.3.1 样本熵(S…...

【Go语言基础【12】】指针:声明、取地址、解引用
文章目录 零、概述:指针 vs. 引用(类比其他语言)一、指针基础概念二、指针声明与初始化三、指针操作符1. &:取地址(拿到内存地址)2. *:解引用(拿到值) 四、空指针&am…...

关于easyexcel动态下拉选问题处理
前些日子突然碰到一个问题,说是客户的导入文件模版想支持部分导入内容的下拉选,于是我就找了easyexcel官网寻找解决方案,并没有找到合适的方案,没办法只能自己动手并分享出来,针对Java生成Excel下拉菜单时因选项过多导…...

抽象类和接口(全)
一、抽象类 1.概念:如果⼀个类中没有包含⾜够的信息来描绘⼀个具体的对象,这样的类就是抽象类。 像是没有实际⼯作的⽅法,我们可以把它设计成⼀个抽象⽅法,包含抽象⽅法的类我们称为抽象类。 2.语法 在Java中,⼀个类如果被 abs…...

mac:大模型系列测试
0 MAC 前几天经过学生优惠以及国补17K入手了mac studio,然后这两天亲自测试其模型行运用能力如何,是否支持微调、推理速度等能力。下面进入正文。 1 mac 与 unsloth 按照下面的进行安装以及测试,是可以跑通文章里面的代码。训练速度也是很快的。 注意…...

如何配置一个sql server使得其它用户可以通过excel odbc获取数据
要让其他用户通过 Excel 使用 ODBC 连接到 SQL Server 获取数据,你需要完成以下配置步骤: ✅ 一、在 SQL Server 端配置(服务器设置) 1. 启用 TCP/IP 协议 打开 “SQL Server 配置管理器”。导航到:SQL Server 网络配…...

【iOS】 Block再学习
iOS Block再学习 文章目录 iOS Block再学习前言Block的三种类型__ NSGlobalBlock____ NSMallocBlock____ NSStackBlock__小结 Block底层分析Block的结构捕获自由变量捕获全局(静态)变量捕获静态变量__block修饰符forwarding指针 Block的copy时机block作为函数返回值将block赋给…...

GAN模式奔溃的探讨论文综述(一)
简介 简介:今天带来一篇关于GAN的,对于模式奔溃的一个探讨的一个问题,帮助大家更好的解决训练中遇到的一个难题。 论文题目:An in-depth review and analysis of mode collapse in GAN 期刊:Machine Learning 链接:...

leetcode_69.x的平方根
题目如下 : 看到题 ,我们最原始的想法就是暴力解决: for(long long i 0;i<INT_MAX;i){if(i*ix){return i;}else if((i*i>x)&&((i-1)*(i-1)<x)){return i-1;}}我们直接开始遍历,我们是整数的平方根,所以我们分两…...
