Acwing---843. n-皇后问题
n-皇后问题
- 1.题目
- 2.基本思想
- 3.代码实现
1.题目
n−皇后问题是指将 n 个皇后放在 n×n 的国际象棋棋盘上,使得皇后不能相互攻击到,即任意两个皇后都不能处于同一行、同一列或同一斜线上。
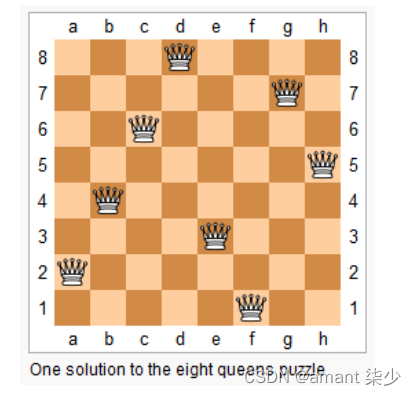
现在给定整数 n,请你输出所有的满足条件的棋子摆法。
输入格式
共一行,包含整数 n。
输出格式
每个解决方案占 n 行,每行输出一个长度为 n 的字符串,用来表示完整的棋盘状态。
其中 . 表示某一个位置的方格状态为空,Q 表示某一个位置的方格上摆着皇后。
每个方案输出完成后,输出一个空行。
注意:行末不能有多余空格。
输出方案的顺序任意,只要不重复且没有遗漏即可。
数据范围
1≤n≤91≤n≤91≤n≤9
输入样例:
4
输出样例:
.Q…
…Q
Q…
…Q.
…Q.
Q…
…Q
.Q…
2.基本思想
DFS 时间复杂度O(n!)
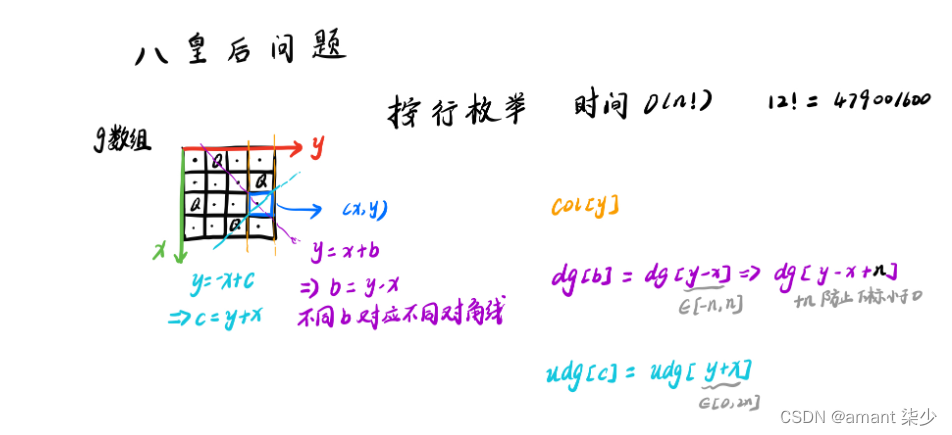
正对角线,y=-x+c,c=x+y,c这里代表截距,反对角线y=x+c,c=y-x,所以这里的c可能是负的,但作为数组下标,不能是负的,所以我们把反对角线加上一个偏移量,c=y-x+n是没影响的,因为截距最大是n,也可以加比n大的任何数
用截距表示对角线,截距相同就说明是同一条对角线
核心目的:找一些合法的下标来表示dg或udg是否被标记过,所以如果你愿意,你取 udg[n+n−u+i]
也可以,只要所有(u,i)对可以映射过去就行.
3.代码实现
import java.util.Scanner;public class _843n皇后问题 {static Scanner sc = new Scanner(System.in);static int N = 20;//增加 了一个 偏移量 n 需要 开 20static int n;static char path[][] = new char[N][N];//保存 路径信息static boolean[] col = new boolean[N];// bool数组用来判断搜索的下一个位置是否可行 col列,dg对角线,udg反对角线static boolean[] dg = new boolean[N];static boolean[] udg = new boolean[N];public static void main(String[] args) {n = sc.nextInt();for (int i = 0; i < n; i++)for (int j = 0; j < n; j++)path[i][j] = '.';dfs(0);}private static void dfs(int u) {if (u == n) {//表示 已经搜素了n行 输出这条路径 信息for (int i = 0; i < n; i++) {for (int j = 0; j < n; j++)System.out.print(path[i][j]);System.out.println();//换行}System.out.println();return;}//对n个位置按行搜索for (int i = 0; i < n; i++) {if (!col[i] && !dg[i + u] && !udg[n + i - u]) {path[u][i] = 'Q';col[i] = dg[u + i] = udg[n + i - u] = true;dfs(u + 1);//枚举 下一行//恢复 回溯col[i] = dg[u + i] = udg[n + i - u] = false;path[u][i] = '.';}}}
}
相关文章:

Acwing---843. n-皇后问题
n-皇后问题1.题目2.基本思想3.代码实现1.题目 n−皇后问题是指将 n 个皇后放在 nn 的国际象棋棋盘上,使得皇后不能相互攻击到,即任意两个皇后都不能处于同一行、同一列或同一斜线上。 现在给定整数 n,请你输出所有的满足条件的棋子摆法。 …...

彻底搞清楚内存泄漏的原因,如何避免内存泄漏,如何定位内存泄漏
作为C/C开发人员,内存泄漏是最容易遇到的问题之一,这是由C/C语言的特性引起的。C/C语言与其他语言不同,需要开发者去申请和释放内存,即需要开发者去管理内存,如果内存使用不当,就容易造成段错误(segment fa…...
自动驾驶目标检测项目实战——基于深度学习框架yolov的交通标志检测
自动驾驶目标检测项目实战——基于深度学习框架yolov的交通标志检测 目前目标检测算法有很多,流行的就有faster-rnn和yolov,本文使用了几年前的yolov3框架进行训练,效果还是很好,当然也可以使用更高版本的Yolov进行实战。本代码使…...

flink兼容性验证
flink介绍:https://blog.csdn.net/weixin_43563705/article/details/107604693 一、安装启动 安装flink及其依赖 yum install java-1.8.0-openjdk curl tar mkdir -p /usr/local/flink wget https://mirrors.aliyun.com/apache/flink/flink-1.16.1/flink-1.16.1-bi…...

智慧工厂数字孪生可视化监测系统有效提升厂区安全管控效力
我国制造业正处于产业升级的关键时期,基于数据进行生产策略制定与管理是大势所趋,而数据可视化以更直观的方式成为数据分析传递信息的重要工具。 深圳华锐视点通过三维可视化手段对工厂各类设备进行三维建模,真实复现设备设施外观、结构、运转…...

c++中基本类型详细解释外加基本运算规则
👀👀#c中包括算数类型和空类型。 类型含义wchat_t宽字符bool布尔类型char字符chat16_tunicode字符chat_32unicode字符short短整型int整形long长整型longlong长整型float单精度浮点型double双精度浮点型longdouble扩展精度浮点型 👀…...

扬帆优配“机器人+”方案加码产业发展,这些股有望高增长
“机器人”发明新需求,2022年中国机器人市场规模约为174亿美元。 美国时刻3月1日,特斯拉在得克萨斯州超级工厂举办投资者日活动,展示了人形机器人Optimus的视频,更夸大的是,视频中的机器人好像在制作另一个机器人&…...
推送投票制作微信推送里投票制作教程在线投票活动制作
近些年来,第三方的微信投票制作平台如雨后春笋般络绎不绝。随着手机的互联网的发展及微信开放平台各项基于手机能力的开放,更多人选择微信投票小程序平台,因为它有非常大的优势。1.它比起微信公众号自带的投票系统、传统的H5投票系统有可以图…...
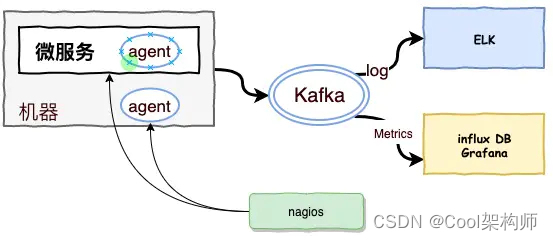
【架构师】跟我一起学架构——微服务分层监控
博客昵称:架构师Cool 最喜欢的座右铭:一以贯之的努力,不得懈怠的人生。 作者简介:一名Coder,软件设计师/鸿蒙高级工程师认证,在备战高级架构师/系统分析师,欢迎关注小弟! 博主小留言…...
Linux:https静态网站搭建案例
目录介绍httpshttps通信过程例介绍https 整个实验是在http实验基础上进行的 因为http协议在传输的时候采用的是明文传输,有安全隐患,所以出现了https(安全套接字层超文本传输协议) HTTPS并不是一个新协议, 而是HTTP…...

前端css整理
如何水平垂直居中一个盒子? 1.已知高度:子盒子设置 display: inline-block; 父盒子设置 line-height 等于高度实现垂直居中;使用 text-align:center实现水平居中 2.父盒子 display:flex; align-items:center;justify-content:center; 3.定位&…...

混凝土搅拌站远程监控解决方案
一、项目背景 随着大规模的基础设施建设,对混凝土搅拌设备的需求量日益增加,对其技术指标的要求也日益提高,其技术性能将直接关系到工程的质量和使用寿命。而混凝土生产的质量是在生产过程中形成的,而非最终强度的检测。混凝土生…...

Spark SQL 学习总结
文章目录(一)Spark SQL(二)SParkSession(三)DataFrame常见算子操作(四)DataFrame的sql操作(五)RDD转换为DataFrame(1)反射方式&#x…...

深度学习 - 37.TF x Keras Deep Cross Network DCN 实现
目录 一.引言 二.模型简介 1.Embedding and stacking layer 2.Cross Network 2.1 模型架构分析 2.2 计算逻辑...
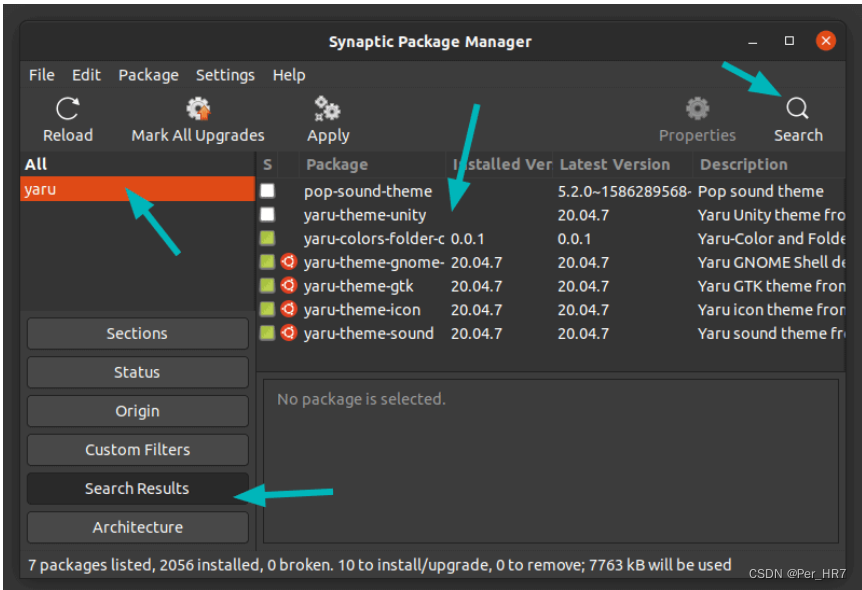
Ubuntu中使用Synaptic进行包管理
Synaptic概况 Synaptic 是一个轻量级的 apt 软件包管理器系统的 GUI 前端,所有你可以在终端中使用 apt-get 命令来做的事,都可以通过 Synaptic 来实现。优势 图形化安装界面,同时可以安装配置相关依赖,避免由于依赖问题导致的各类…...

python之selenium库安装及用法(定位法、获取文本、文本框输入、鼠标点击、滑动滚动条)
一、selenium库安装 pip install selenium二、浏览器驱动安装 谷歌浏览器驱动下载地址:https://chromedriver.storage.googleapis.com/index.html 根据你电脑的谷歌浏览器版本,下载相应的就行。我下载的是110.0.5481.XX中的chromedriver_win32.zip 下载…...

FPGA纯verilog实现图像视频旋转 串口指令控制旋转角度 提供工程源码和技术支持
目录1、前言2、理论基础3、设计思路和框架图像输入和采集图像旋转处理图像缓存图像输出4、vivado工程详解5、上板调试验证6、福利:工程代码的获取1、前言 图像旋转是一种常用的图像处理技术,其基本原理就是指图像以某一点为中心旋转一定的角度ÿ…...

EventGraph:Event Extraction as Semantic Graph Parsing 论文解读
EventGraph: Event Extraction as Semantic Graph Parsing 论文:2022.case-1.2.pdf (aclanthology.org) 代码:huiling-y/EventGraph (github.com) 期刊/会议:CASE 2022 摘要 事件抽取涉及到事件触发词和相应事件论元的检测和抽取。现有系…...

【蓝桥杯集训·每日一题】AcWing 3696. 构造有向无环图
文章目录一、题目1、原题链接2、题目描述二、解题报告1、思路分析2、时间复杂度3、代码详解三、知识风暴拓扑排序一、题目 1、原题链接 3696. 构造有向无环图 2、题目描述 给定一个由 n 个点和 m 条边构成的图。 不保证给定的图是连通的。 图中的一部分边的方向已经确定&#…...
国内vs国外:外贸建站该如何选择?
外贸建站找国内还是国外? 答案是:国内。 随着互联网的发展,越来越多的企业开始意识到在网络上进行商业活动的重要性。 其中,建立一个专业的外贸网站是企业在国际市场上拓展业务的关键。 然而,对于选择国内还是国外…...

业务系统对接大模型的基础方案:架构设计与关键步骤
业务系统对接大模型:架构设计与关键步骤 在当今数字化转型的浪潮中,大语言模型(LLM)已成为企业提升业务效率和创新能力的关键技术之一。将大模型集成到业务系统中,不仅可以优化用户体验,还能为业务决策提供…...

【入坑系列】TiDB 强制索引在不同库下不生效问题
文章目录 背景SQL 优化情况线上SQL运行情况分析怀疑1:执行计划绑定问题?尝试:SHOW WARNINGS 查看警告探索 TiDB 的 USE_INDEX 写法Hint 不生效问题排查解决参考背景 项目中使用 TiDB 数据库,并对 SQL 进行优化了,添加了强制索引。 UAT 环境已经生效,但 PROD 环境强制索…...

高频面试之3Zookeeper
高频面试之3Zookeeper 文章目录 高频面试之3Zookeeper3.1 常用命令3.2 选举机制3.3 Zookeeper符合法则中哪两个?3.4 Zookeeper脑裂3.5 Zookeeper用来干嘛了 3.1 常用命令 ls、get、create、delete、deleteall3.2 选举机制 半数机制(过半机制࿰…...

UR 协作机器人「三剑客」:精密轻量担当(UR7e)、全能协作主力(UR12e)、重型任务专家(UR15)
UR协作机器人正以其卓越性能在现代制造业自动化中扮演重要角色。UR7e、UR12e和UR15通过创新技术和精准设计满足了不同行业的多样化需求。其中,UR15以其速度、精度及人工智能准备能力成为自动化领域的重要突破。UR7e和UR12e则在负载规格和市场定位上不断优化…...

今日学习:Spring线程池|并发修改异常|链路丢失|登录续期|VIP过期策略|数值类缓存
文章目录 优雅版线程池ThreadPoolTaskExecutor和ThreadPoolTaskExecutor的装饰器并发修改异常并发修改异常简介实现机制设计原因及意义 使用线程池造成的链路丢失问题线程池导致的链路丢失问题发生原因 常见解决方法更好的解决方法设计精妙之处 登录续期登录续期常见实现方式特…...
)
Typeerror: cannot read properties of undefined (reading ‘XXX‘)
最近需要在离线机器上运行软件,所以得把软件用docker打包起来,大部分功能都没问题,出了一个奇怪的事情。同样的代码,在本机上用vscode可以运行起来,但是打包之后在docker里出现了问题。使用的是dialog组件,…...

LeetCode - 199. 二叉树的右视图
题目 199. 二叉树的右视图 - 力扣(LeetCode) 思路 右视图是指从树的右侧看,对于每一层,只能看到该层最右边的节点。实现思路是: 使用深度优先搜索(DFS)按照"根-右-左"的顺序遍历树记录每个节点的深度对于…...

Python Ovito统计金刚石结构数量
大家好,我是小马老师。 本文介绍python ovito方法统计金刚石结构的方法。 Ovito Identify diamond structure命令可以识别和统计金刚石结构,但是无法直接输出结构的变化情况。 本文使用python调用ovito包的方法,可以持续统计各步的金刚石结构,具体代码如下: from ovito…...

【JVM】Java虚拟机(二)——垃圾回收
目录 一、如何判断对象可以回收 (一)引用计数法 (二)可达性分析算法 二、垃圾回收算法 (一)标记清除 (二)标记整理 (三)复制 (四ÿ…...

MySQL 部分重点知识篇
一、数据库对象 1. 主键 定义 :主键是用于唯一标识表中每一行记录的字段或字段组合。它具有唯一性和非空性特点。 作用 :确保数据的完整性,便于数据的查询和管理。 示例 :在学生信息表中,学号可以作为主键ÿ…...
