制药企业符合CSV验证需要注意什么?
在制药行业中,计算机化系统验证(CSV)是确保生产过程的合规性和数据完整性的关键要素。通过CSV验证,制药企业可以保证其计算机化系统的可靠性和合规性,从而确保产品质量和患者安全。然而,符合CSV验证并不是一项简单的任务,需要制药企业注意一系列关键要点。本文将探讨制药企业在符合CSV验证时需要注意的重要事项。

图.制药企业(Pexel)
1. 建立验证策略和计划
在开始CSV验证之前,制药企业应制定明确的验证策略和计划。验证策略应明确系统的验证目标、范围和方法,以及验证的时间和资源预算。验证计划应详细说明验证活动的顺序、责任人和时间表,确保验证工作按计划进行。
2. 明确用户需求和功能规范
制药企业应与设备健康管理系统(如PreMaint)的使用者密切沟通,明确他们需求和功能使用规范。用户需求规范应准确描述系统所需的功能和性能,以满足业务需求和法规要求。功能规范应明确系统的功能、界面和交互等方面的要求,确保系统符合预期需求。
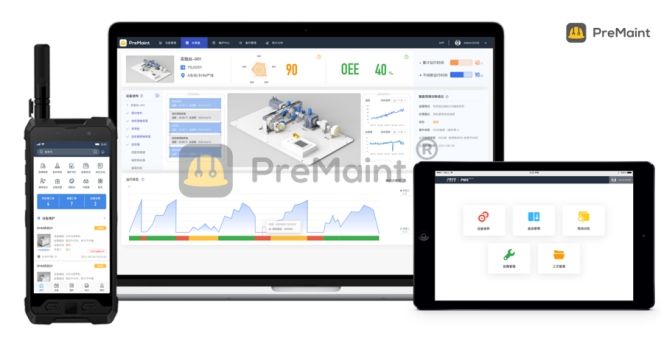
图.设备健康管理系统(PreMaint)
3. 进行验证测试和文档记录
制药企业应制定详细的验证测试计划,并执行相应的验证测试。验证测试应涵盖设备健康管理系统的功能、性能、安全性和数据完整性等方面。测试结果应进行记录和文档化,包括测试报告、问题追踪和修复措施等。验证文档的完整性和准确性至关重要,以便审计和监管机构进行审查。
4. 管理变更控制和版本控制
在CSV验证过程中,制药企业应建立严格的变更控制和版本控制机制。任何对计算机化系统的更改都应经过适当的变更控制程序,并进行验证和文档记录。版本控制应确保设备健康管理系统的版本和配置信息得到有效管理和跟踪,以防止不受控制的变更对系统的影响。
5. 培训和人员资质
制药企业应为相关人员提供充分的培训,确保他们具备执行CSV验证所需的知识和技能。培训应包括设备健康管理系统操作、验证测试、文档记录和变更控制等方面。此外,制药企业还应确保相关人员具备适当的资质和经验,以保证验证工作的质量和可靠性。
6. 定期评估和持续改进
CSV验证并非一次性工作,制药企业应定期评估验证结果和设备健康管理系统性能,并进行持续改进。通过评估验证结果,制药企业可以识别潜在的设备问题和改进机会,并采取相应的预测性维护措施。持续改进可以不断提高验证的效率和质量,确保计算机化系统始终符合法规要求和最佳实践。
更多制药企业CSV验证的相关内容,可参考>>制药企业的设备健康管理系统为何要符合计算机化系统验证CSV?
符合CSV验证对于制药企业来说至关重要,它确保了计算机化系统的可靠性、合规性和数据完整性。在符合CSV验证过程中,制药企业需要注意的要点有很多。通过遵循这些关键要点,PreMaint设备健康管理系统可以确保制药企业有效符合CSV验证,保障产品质量、合规性和患者安全。此外,持续改进也能够提高验证工作的效率和质量,为制药企业带来更大的竞争优势和长期可持续发展。
-关注我,不错过工业互联网&设备管理领域的热点资讯、深度干货!
-如果对本文有任何疑问,或想了解更多内容,欢迎评论留言/发送私信告诉我~
相关文章:

制药企业符合CSV验证需要注意什么?
在制药行业中,计算机化系统验证(CSV)是确保生产过程的合规性和数据完整性的关键要素。通过CSV验证,制药企业可以保证其计算机化系统的可靠性和合规性,从而确保产品质量和患者安全。然而,符合CSV验证并不是一…...

再谈动态SQL
专栏精选 引入Mybatis Mybatis的快速入门 Mybatis的增删改查扩展功能说明 mapper映射的参数和结果 Mybatis复杂类型的结果映射 Mybatis基于注解的结果映射 Mybatis枚举类型处理和类型处理器 再谈动态SQL Mybatis配置入门 Mybatis行为配置之Ⅰ—缓存 Mybatis行为配置…...
【数据结构】树
一.二叉树的基本概念和性质: 1.二叉树的递归定义: 二叉树或为空树,或是由一个根结点加上两棵分别称为左子树和右子树的、互不相交的二叉树组成 2.二叉树的特点: (1)每个结点最多只有两棵子树࿰…...
【Midjourney】AI绘画新手教程(一)登录和创建服务器,生成第一幅画作
一、登录Discord 1、访问Discord官网 使用柯學尚网(亲测非必须,可加快响应速度)访问Discord官方网址:https://discord.com 选择“在您的浏览器中打开Discord” 然后,注册帐号、购买套餐等,在此不做缀述。…...

对比 PyTorch 和 TensorFlow:选择适合你的深度学习框架
目录 引言 深度学习在各行业中的应用 PyTorch 和 TensorFlow 简介 PyTorch:简介与设计理念 发展历史和背景 主要特点和设计理念 TensorFlow:简介与设计理念 发展历史和背景 主要特点和设计理念 PyTorch 和 TensorFlow 的重要性 Pytorch对比Te…...

Oracle笔记-查看表已使用空间最大空间
目前以Oracle18c为例,主要是查这个表USER_SEGMENTS。 在 Oracle 18c 数据库中,USER_SEGMENTS 是一个系统表,用于存储当前用户(当前会话)拥有的所有段的信息。段是 Oracle 中分配存储空间的逻辑单位,用于存…...

大数据HCIE成神之路之特征工程——特征选择
特征选择 1.1 特征选择 - Filter方法1.1.1 实验任务1.1.1.1 实验背景1.1.1.2 实验目标1.1.1.3 实验数据解析1.1.1.4 实验思路 1.1.2 实验操作步骤 1.2 特征选择 - Wrapper方法1.2.1 实验任务1.2.1.1 实验背景1.2.1.2 实验目标1.2.1.3 实验数据解析1.2.1.4 实验思路 1.2.2 实验操…...

python 正则-常见题目
1、邮箱 print(re.findall(r[\w-][\w-]\.[\w-], weidianqq.com))2、身份证号 xxxxxx yyyy MM dd 375 0 十八位 print(re.findall(r(?:18|19|(?:[23]\d))\d{2}, 2010)) # 年print(re.findall(r(?:0[1-9])|10|11|12, 11)) # 月print(re.findall(r(?:[0-2][1-9])|10|20|30|3…...

解析:Eureka的工作原理
Eureka是Netflix开源的一个基于REST的的服务发现注册框架,它遵循了REST协议,提供了一套简单的API来完成服务的注册和发现。Eureka能够帮助分布式系统中的服务提供者自动将自身注册到注册中心,同时也能够让服务消费者从注册中心发现服务提供者…...

RecyclerView 与 ListView 区别和使用
前置知识:ListView基本用法与性能提升 RecyclerView 与 ListView 区别 RecyclerView 需要设置布局(LinearLayoutManager、GridLayoutManager、StaggeredGridLayoutManager) recyclerView?.layoutManager LinearLayoutManager(activity) …...

力扣232. 用栈实现队列
题目 请你仅使用两个栈实现先入先出队列。队列应当支持一般队列支持的所有操作(push、pop、peek、empty): 实现 MyQueue 类: void push(int x) 将元素 x 推到队列的末尾int pop() 从队列的开头移除并返回元素int peek() 返回队列开…...
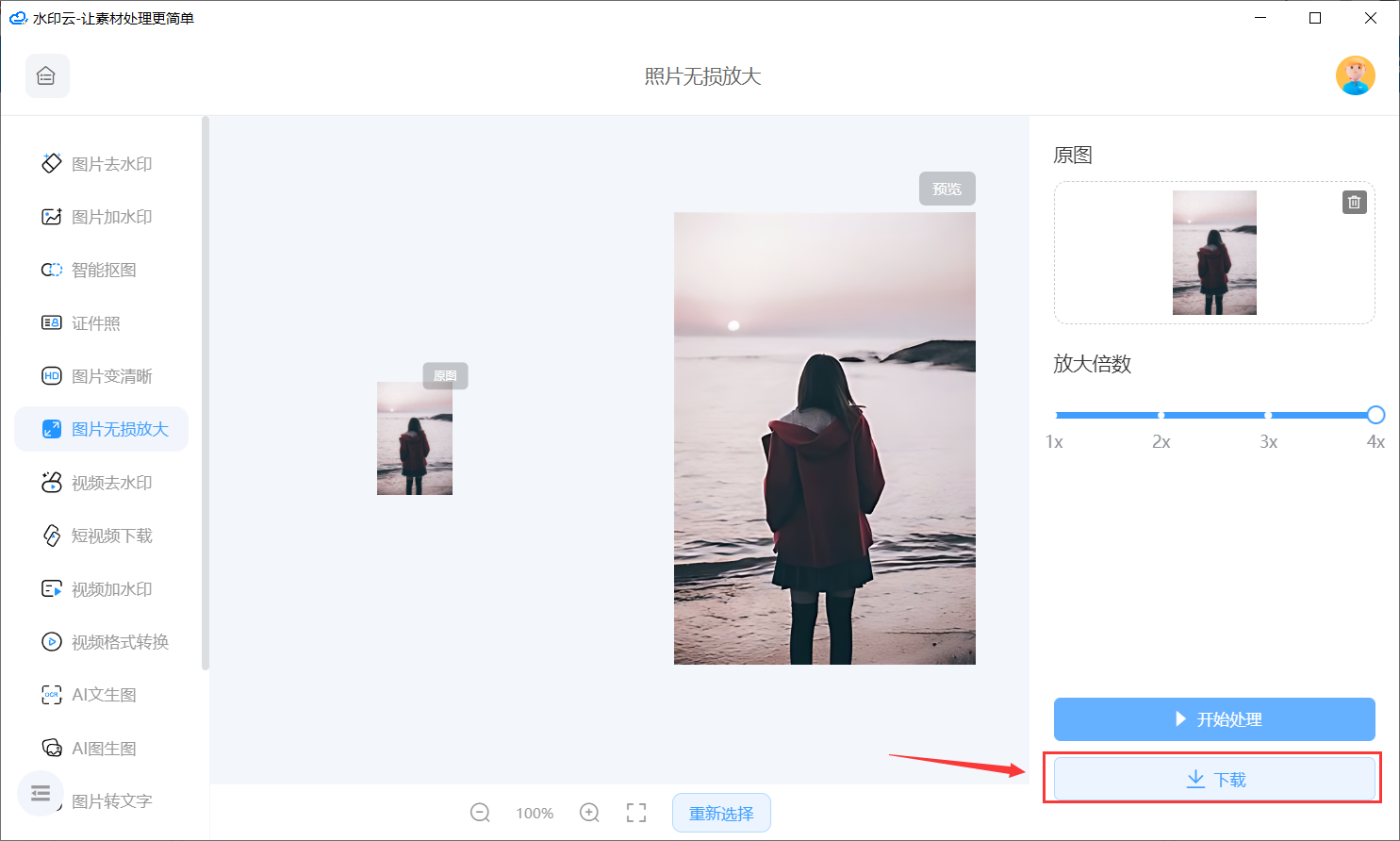
这个方法可以让你把图片无损放大
随着数字技术的不断发展,照片无损放大已经成为了摄影领域中的一项重要技术。照片无损放大能够让摄影师在不损失细节和画质的情况下,将照片放大到更大的尺寸,从而让观众能够更加清晰地欣赏到照片中的每一个细节。 今天推荐的这款软件主要是通…...

Springboot整合Elastic-job
一 概述 Elastic-Job 最开始只有一个 elastic-job-core 的项目,定位轻量级、无中心化,最核心的服务就是支持弹性扩容和数据分片!从 2.X 版本以后,主要分为 Elastic-Job-Lite 和 Elastic-Job-Cloud 两个子项目。esjbo官网地址 Ela…...
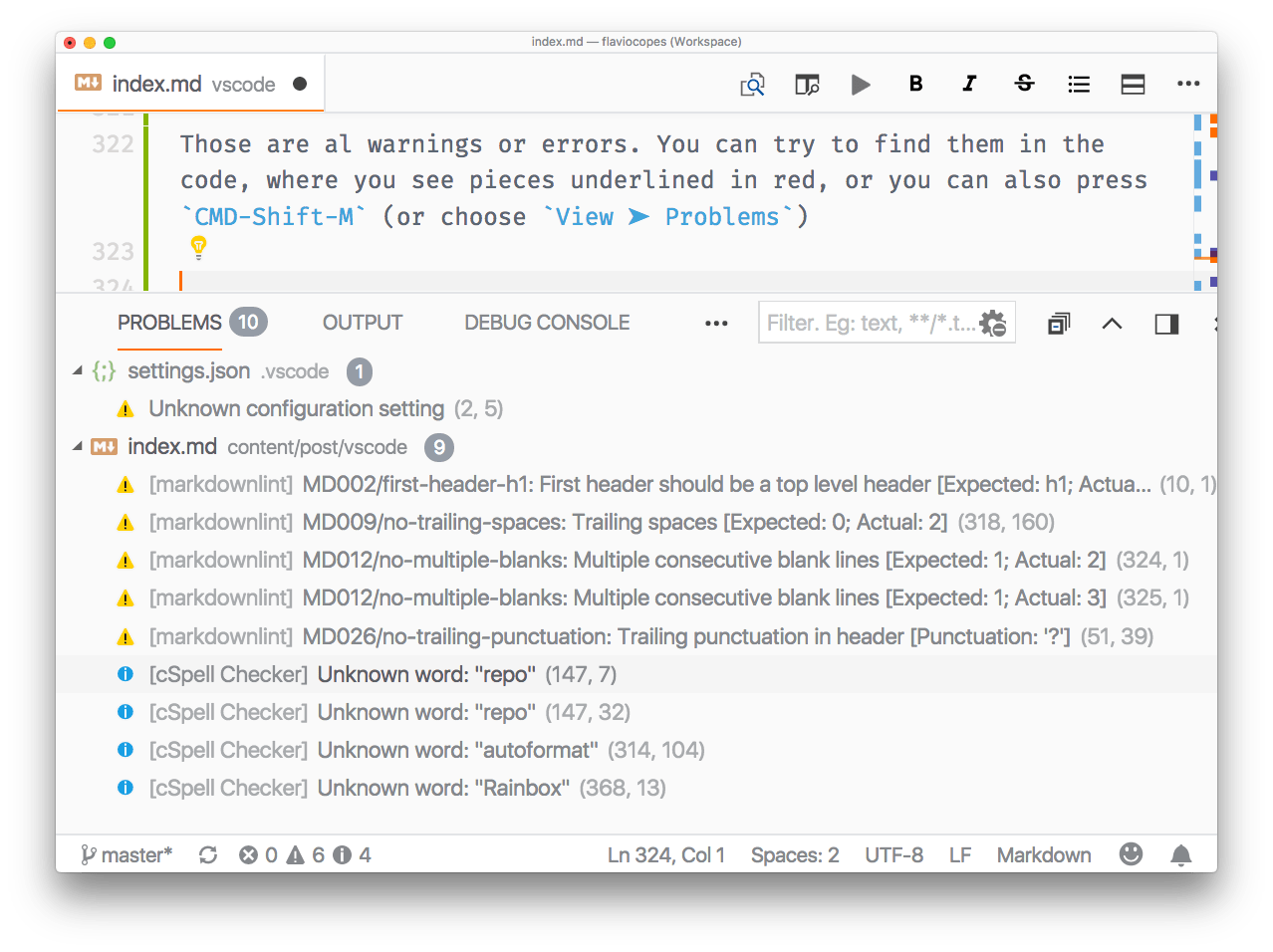
VsCode的介绍和入门
目录 编辑 介绍 我应该切换到 VS Code 吗?为什么? 入门 Explorer 搜索 源代码控制 调试器 扩展 终点站 命令面板 主题 定制化 不错的配置选项 最适合编码的字体 工作空间 编辑 智能感知 代码格式化 错误和警告 键盘快捷键 键位图…...

C++:自创小游戏
欢迎来玩,每次都有不一样的结果。 长达142行。 #include<bits/stdc.h> #include<windows.h> #define random(a,b) (rand()%(b-a1)a) using namespace std; int main(){int n;cout<<"输1~10,越小越好,不告诉你有什么用,当然也可…...

AIGC带给开发者的冲击
未来会有两种开发者,一种是会使用AIGC工具的开发者另一种是不会使用AIGC的开发者,AIGC的出现提高了开发效率和代码质量,对开发者意味着需要不断学习和适应新的技术和工作范式,开发者可以把更多的精力放在高级抽象的定义以及更高维…...
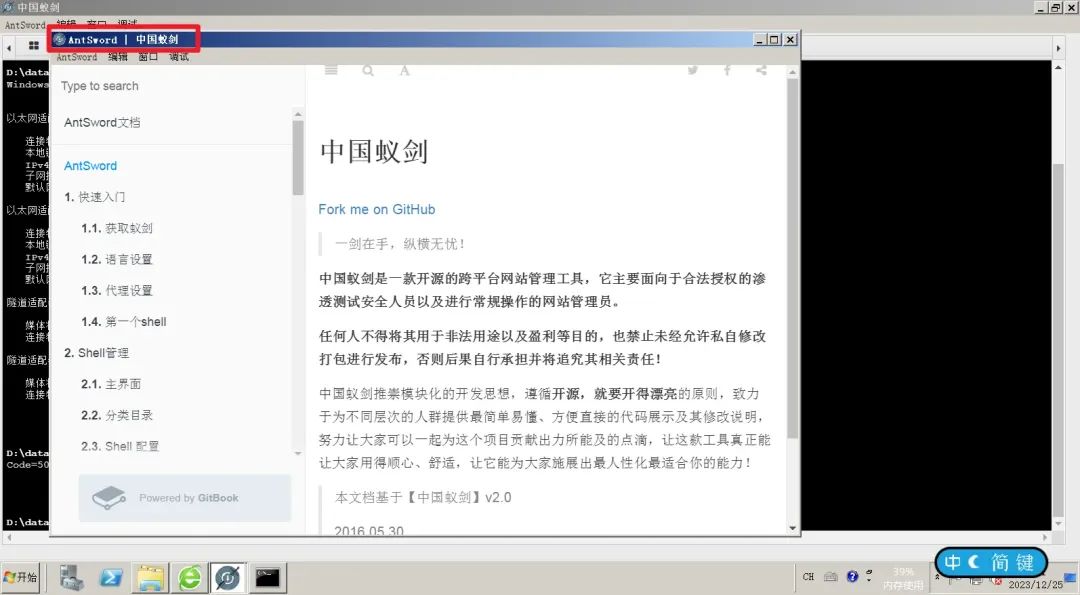
利用蚁剑钓鱼上线CS
前言 中国蚁剑使用Electron构建客户端软件,Electron实现上用的是Node.js,并且Node.js能执行系统命令,故可以利用蚁剑的webshell页面嵌入js来直接执行命令,进而钓鱼来上线CS。(类似Goby,Goby也是使用Electr…...

宣传照(私密)勿转发
精美的海报通常都是由UI进行精心设计的,现在有100 件商品需要进行宣传推广,如果每个商品都出一张图显然是不合理的,且商品信息各异。因此需要通过代码的形式生成海报。对此,我也对我宣传一波,企图实现我一夜暴富的伟大…...

【Spring】19 AOP介绍及实例详解
文章目录 1. 定义1)什么意思呢?2)如何解决呢? 2. 基本概念1)切面(Aspect)2)切点(Pointcut)3)通知(Advice)4)连…...
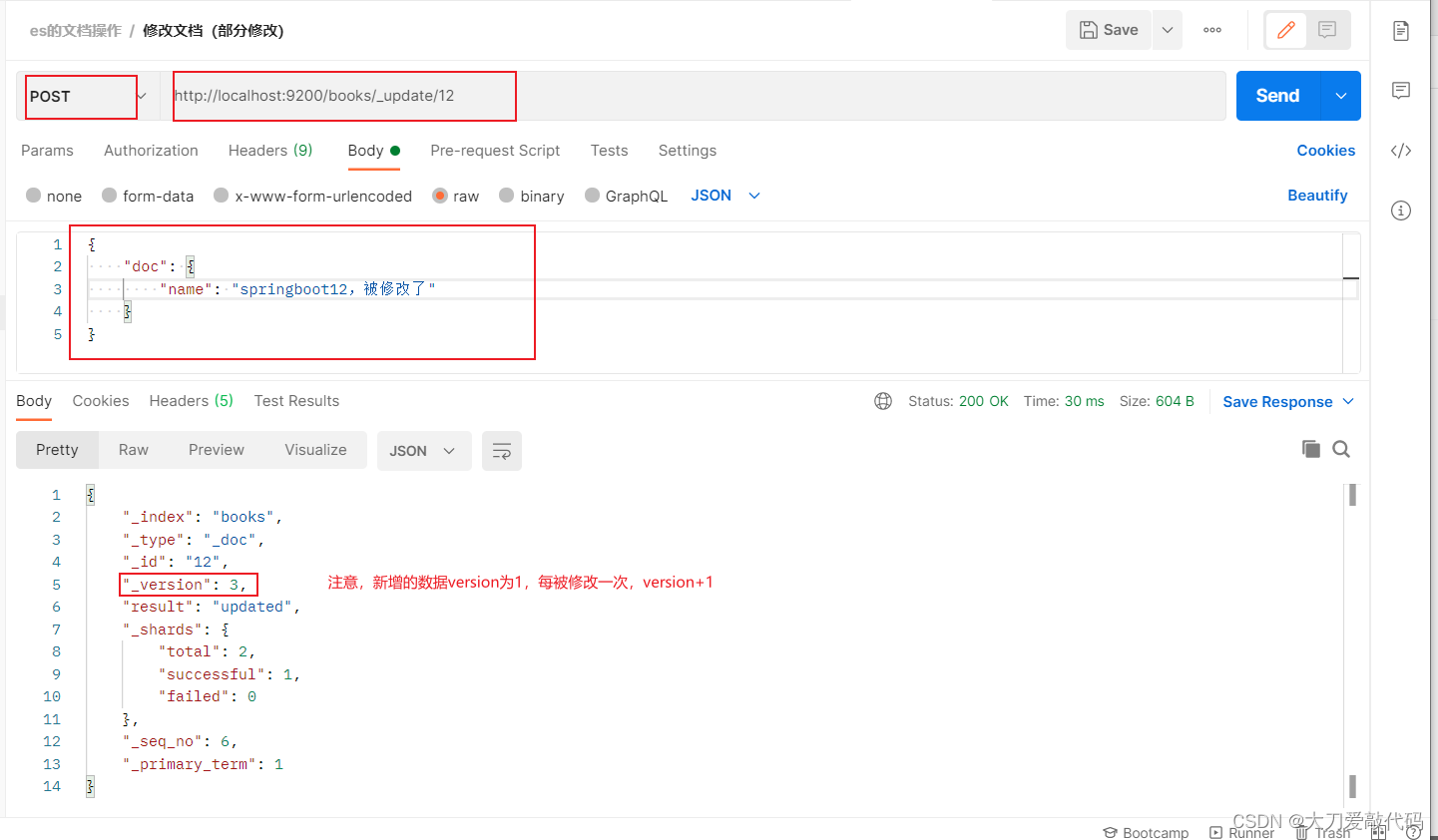
ES(Elasticsearch)的基本使用
一、常见的NoSQL解决方案 1、redis Redis是一个基于内存的 key-value 结构数据库。Redis是一款采用key-value数据存储格式的内存级NoSQL数据库,重点关注数据存储格式,是key-value格式,也就是键值对的存储形式。与MySQL数据库不同࿰…...

iOS 26 携众系统重磅更新,但“苹果智能”仍与国行无缘
美国西海岸的夏天,再次被苹果点燃。一年一度的全球开发者大会 WWDC25 如期而至,这不仅是开发者的盛宴,更是全球数亿苹果用户翘首以盼的科技春晚。今年,苹果依旧为我们带来了全家桶式的系统更新,包括 iOS 26、iPadOS 26…...

Leetcode 3576. Transform Array to All Equal Elements
Leetcode 3576. Transform Array to All Equal Elements 1. 解题思路2. 代码实现 题目链接:3576. Transform Array to All Equal Elements 1. 解题思路 这一题思路上就是分别考察一下是否能将其转化为全1或者全-1数组即可。 至于每一种情况是否可以达到…...
)
椭圆曲线密码学(ECC)
一、ECC算法概述 椭圆曲线密码学(Elliptic Curve Cryptography)是基于椭圆曲线数学理论的公钥密码系统,由Neal Koblitz和Victor Miller在1985年独立提出。相比RSA,ECC在相同安全强度下密钥更短(256位ECC ≈ 3072位RSA…...

Zustand 状态管理库:极简而强大的解决方案
Zustand 是一个轻量级、快速和可扩展的状态管理库,特别适合 React 应用。它以简洁的 API 和高效的性能解决了 Redux 等状态管理方案中的繁琐问题。 核心优势对比 基本使用指南 1. 创建 Store // store.js import create from zustandconst useStore create((set)…...

MMaDA: Multimodal Large Diffusion Language Models
CODE : https://github.com/Gen-Verse/MMaDA Abstract 我们介绍了一种新型的多模态扩散基础模型MMaDA,它被设计用于在文本推理、多模态理解和文本到图像生成等不同领域实现卓越的性能。该方法的特点是三个关键创新:(i) MMaDA采用统一的扩散架构…...

Maven 概述、安装、配置、仓库、私服详解
目录 1、Maven 概述 1.1 Maven 的定义 1.2 Maven 解决的问题 1.3 Maven 的核心特性与优势 2、Maven 安装 2.1 下载 Maven 2.2 安装配置 Maven 2.3 测试安装 2.4 修改 Maven 本地仓库的默认路径 3、Maven 配置 3.1 配置本地仓库 3.2 配置 JDK 3.3 IDEA 配置本地 Ma…...

MySQL账号权限管理指南:安全创建账户与精细授权技巧
在MySQL数据库管理中,合理创建用户账号并分配精确权限是保障数据安全的核心环节。直接使用root账号进行所有操作不仅危险且难以审计操作行为。今天我们来全面解析MySQL账号创建与权限分配的专业方法。 一、为何需要创建独立账号? 最小权限原则…...

C/C++ 中附加包含目录、附加库目录与附加依赖项详解
在 C/C 编程的编译和链接过程中,附加包含目录、附加库目录和附加依赖项是三个至关重要的设置,它们相互配合,确保程序能够正确引用外部资源并顺利构建。虽然在学习过程中,这些概念容易让人混淆,但深入理解它们的作用和联…...

scikit-learn机器学习
# 同时添加如下代码, 这样每次环境(kernel)启动的时候只要运行下方代码即可: # Also add the following code, # so that every time the environment (kernel) starts, # just run the following code: import sys sys.path.append(/home/aistudio/external-libraries)机…...

【JavaSE】多线程基础学习笔记
多线程基础 -线程相关概念 程序(Program) 是为完成特定任务、用某种语言编写的一组指令的集合简单的说:就是我们写的代码 进程 进程是指运行中的程序,比如我们使用QQ,就启动了一个进程,操作系统就会为该进程分配内存…...
