图的遍历(搜索)算法(深度优先算法DFS和广度优先算法BFS)
一、图的遍历的定义:
从图的某个顶点出发访问遍图中所有顶点,且每个顶点仅被访问一次。(连通图与非连通图)
二、深度优先遍历(DFS);
1、访问指定的起始顶点;
2、若当前访问的顶点的邻接顶点有未被访问的,则任选一个访问之;反之,退回到最近访问过的顶点;直到与起始顶点相通的全部顶点都访问完毕;
3、若此时图中尚有顶点未被访问,则再选其中一个顶点作为起始顶点并访问之,转 2; 反之,遍历结束。
连通图的深度优先遍历类似于树的先根遍历
1、如何判别V的邻接点是否被访问?
解决办法:为每个顶点设立一个“访问标志”。首先将图中每个顶点的访问标志设为 FALSE, 之后搜索图中每个顶点,如果未被访问,则以该顶点为起始点,进行深度
优先遍历,否则继续检查下一顶点。
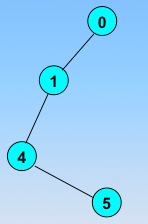
访问指定的起始顶点;若当前访问的顶点的邻接顶点有未被访问的,则任选一个访问之;
反之,退回到最近访问过的顶点;直到与起始顶点相通的全部顶点都访问完毕;
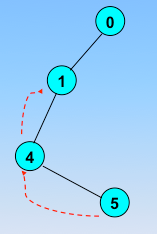
回退到1,发现了新的没有被访问的结点
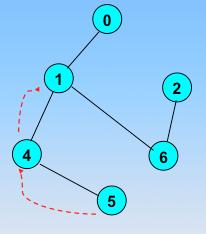
继续回退,回退到0
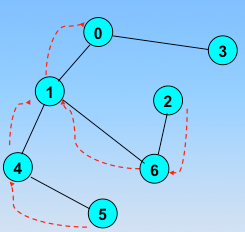
再也找不到新的结点了,那么回退,回退到起始顶点,结束搜索
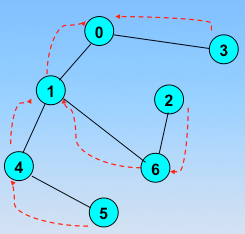
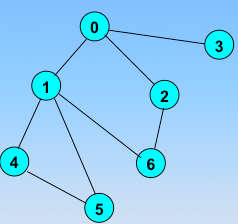
顶点的访问序列为: v0 , v1 , v4 , v5 , v6 , v2 , v3(不唯一)
2、实现过程:依靠栈,一维数组和图的邻接矩阵存储方式
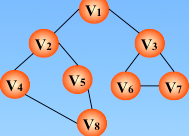
图的邻接矩阵存储方式
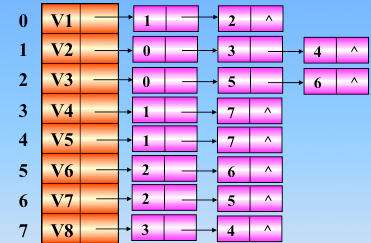
使用一个一维数组存储所有的顶点,对应的下标的元素为1(代表已经被访问),0(代表没有被访问)

先访问 v1,0进栈,0处置为1
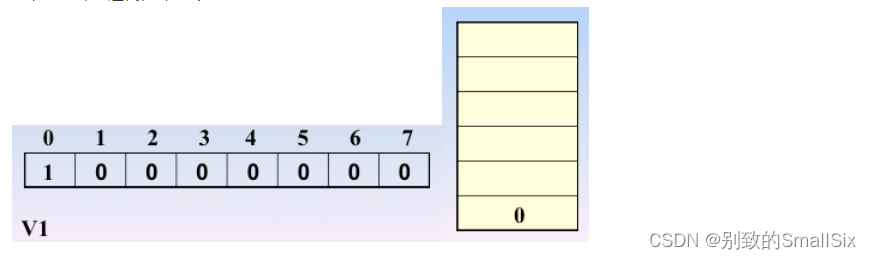
继续访问 v2,1进栈,1处置为1
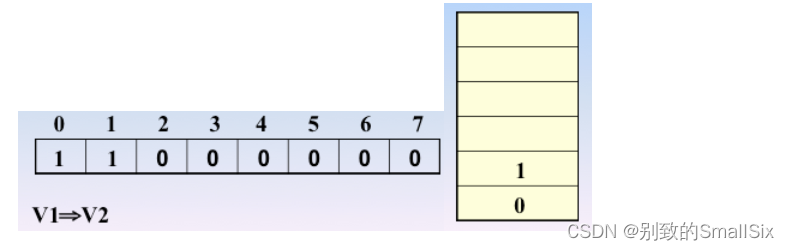
继续访问v4(依据邻接矩阵),3入栈,3处置为1
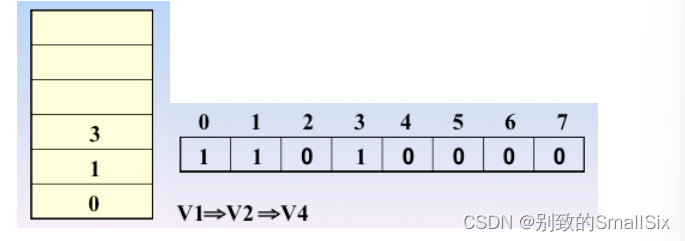
继续访问 v8,7入栈,7处置为1
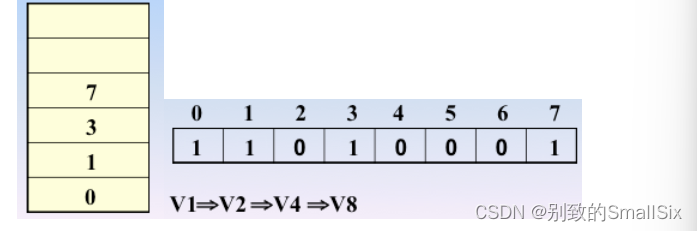
继续访问 v5,4入栈,4处置为1
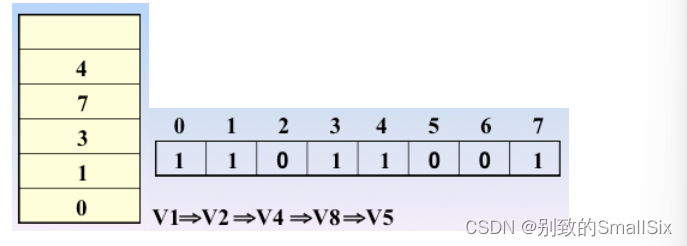
继续访问,发现没有还没访问的结点了,那么好,退栈(也就是回退)开始,回退到 v1处,也就是0的时候,发现了没有被访问的结点,那么继续访问之
继续访问 v3,2进栈,2处置为1,继续访问v6,5进栈,5处置为1,继续访问v7,6进栈,6处置为1
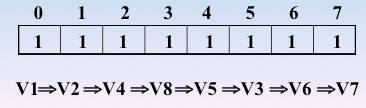
发现没有还没被访问的结点了,那么好,继续回退(也就是退栈的过程)

一直到栈空,说明深度优先搜索完毕。结束程序。
遍历图的过程实质上是对每个顶点查找其邻接点的过程,所耗费的时间取决于所采用的存储结构。
对图中的每个顶点至多调用1次DFS算法,因为一旦某个顶点已访问过,则不再从它出发进行搜索。
邻接链表表示:查找每个顶点的邻接点所需时间为O(e),e为边(弧)数,算法时间复杂度为O(n+e)。
数组表示:查找每个顶点的邻接点所需时间为O(n2),n为顶点数,算法时间复杂度为O(n2)。
3、代码实现
//访问标志数组
int visited[MAX] = {0};
//用邻接表方式实现深度优先搜索(递归方式)
//v 传入的是第一个需要访问的顶点
void DFS(MGraph G, int v)
{
//图的顶点的搜索指针
ArcNode *p;
//置已访问标记
visited[v] = 1;
//输出被访问顶点的编号
printf("%d ", v);
//p指向顶点v的第一条弧的弧头结点
p = G.vertices[v].firstarc;
while (p != NULL)
{
//若p->adjvex顶点未访问,递归访问它
if (visited[p->adjvex] == 0)
{
DFS(G, p->adjvex);
}
//p指向顶点v的下一条弧的弧头结点
p = p->nextarc;
}
}
二、度优先搜索(BFS)
方法:从图的某一结点出发,首先依次访问该结点的所有邻接顶点 Vi1, Vi2, …, Vin 再按这些顶点被访问的先后次序依次访问与它们相邻接的所有未被访问的顶点,重复此过程,直至所有顶点均被访问为止。
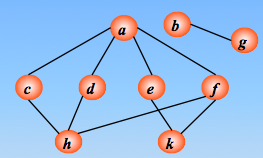
顶点的访问次序
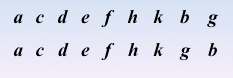
1、实现过程:依靠队列和一维数组来实现
2、代码实现
#include <iostream>
#include<queue>
using namespace std;
const int MAX = 10;
//辅助队列的初始化,置空的辅助队列Q,类似二叉树的层序遍历过程
queue<int> q;
//访问标记数组
bool visited[MAX];
//图的广度优先搜索算法
void BFSTraverse(Graph G, void (*visit)(int v))
{
int v = 0;
//初始化访问标记的数组
for (v = 0; v < G.vexnum; v++)
{
visited[v] = false;
}
//依次遍历整个图的结点
for (v = 0; v < G.vexnum; v++)
{
//如果v尚未访问,则访问 v
if (!visited[v])
{
//把 v 顶点对应的数组下标处的元素置为真,代表已经访问了
visited[v] = true;
//然后v入队列,利用了队列的先进先出的性质
q.push(v);
//访问 v,打印处理
cout << q.back() << " ";
//队不为空时
while (!q.empty())
{
//队头元素出队,并把这个出队的元素置为 u,类似层序遍历
Graph *u = q.front();
q.pop();
//w为u的邻接顶点
for (int w = FirstAdjVex(G, u); w >= 0; w = NextAdjVex(G,u,w))
{
//w为u的尚未访问的邻接顶点
if (!visited[w])
{
visited[w] = true;
//然后 w 入队列,利用了队列的先进先出的性质
q.push(w);
//访问 w,打印处理
cout << q.back() << " ";
}//end of if
}//end of for
}//end of while
}//end of if
}// end of for
}
相关文章:
图的遍历(搜索)算法(深度优先算法DFS和广度优先算法BFS)
一、图的遍历的定义: 从图的某个顶点出发访问遍图中所有顶点,且每个顶点仅被访问一次。(连通图与非连通图) 二、深度优先遍历(DFS); 1、访问指定的起始顶点; 2、若当前访问的顶点…...
抖店做不起来?新手常见起店失败问题总结,看下你中了几条?
我是王路飞。 能看到这篇文章的,肯定是处境符合标题内容了。 抖店的门槛很低,运营思路其实也不算难,但就是很多新手做不起来。 这中间,可能跟平台、项目没什么关系,而是跟你自己有关系,走错了方向&#…...

【每日面试题】精选java面试题之redis
Redis是什么?为什么要使用Redis? Redis是一个开源的高性能键值对存储数据库。它提供了多种数据结构,包括字符串、列表、集合、有序集合、哈希表等。Redis具有快速、可扩展、持久化、支持多种数据结构等特点,适用于缓存、消息队列…...
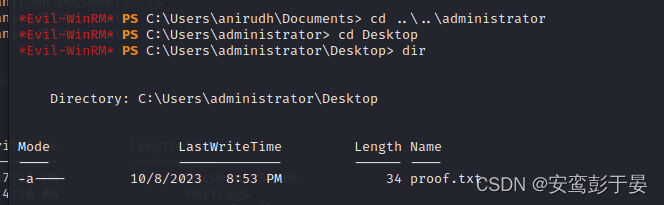
OSCP 靶场 - Vault
端口扫描 nmap nmap -O 192.168.162.172 smb枚举 smbmap(kali自带) //枚举GUEST用户可以使用的目录 smbmap -u GUEST -H 192.168.162.172 NTLMrelay—smbrelay 1.制作钓鱼文件 使用GitHub - xct/hashgrab: generate payloads that force authentication against an attacker…...

uniapp子组件向父组件传值
目录 子组件向父组件传值子组件1子组件2 父组件最后 子组件向父组件传值 子组件1 <template><view class"content"><view v-for"(item,index) in list" :key"index">{{item}}</view></view> </template>&…...

过滤特殊 微信昵称
$nickName preg_replace(/[\xf0-\xf7].{3}/, , $userData[nickName]);...

LLM、AGI、多模态AI 篇一:开源大语言模型简记
文章目录 系列开源大模型LlamaChinese-LLaMA-AlpacaLlama2-ChineseLinlyYaYiChatGLMtransformersGPT-3(未完全开源)BERTT5QwenBELLEMossBaichuan...

微信小程序中获取用户当前位置的解决方案
微信小程序中获取用户当前位置的解决方案 1 概述 微信小程序有时需要获取用户当前位置,以便为用户提供基于位置信息的服务(附近美食、出行方案等)。 获取用户当前位置的前提是用户手机需要打开 GPS 定位开关;其次,微…...
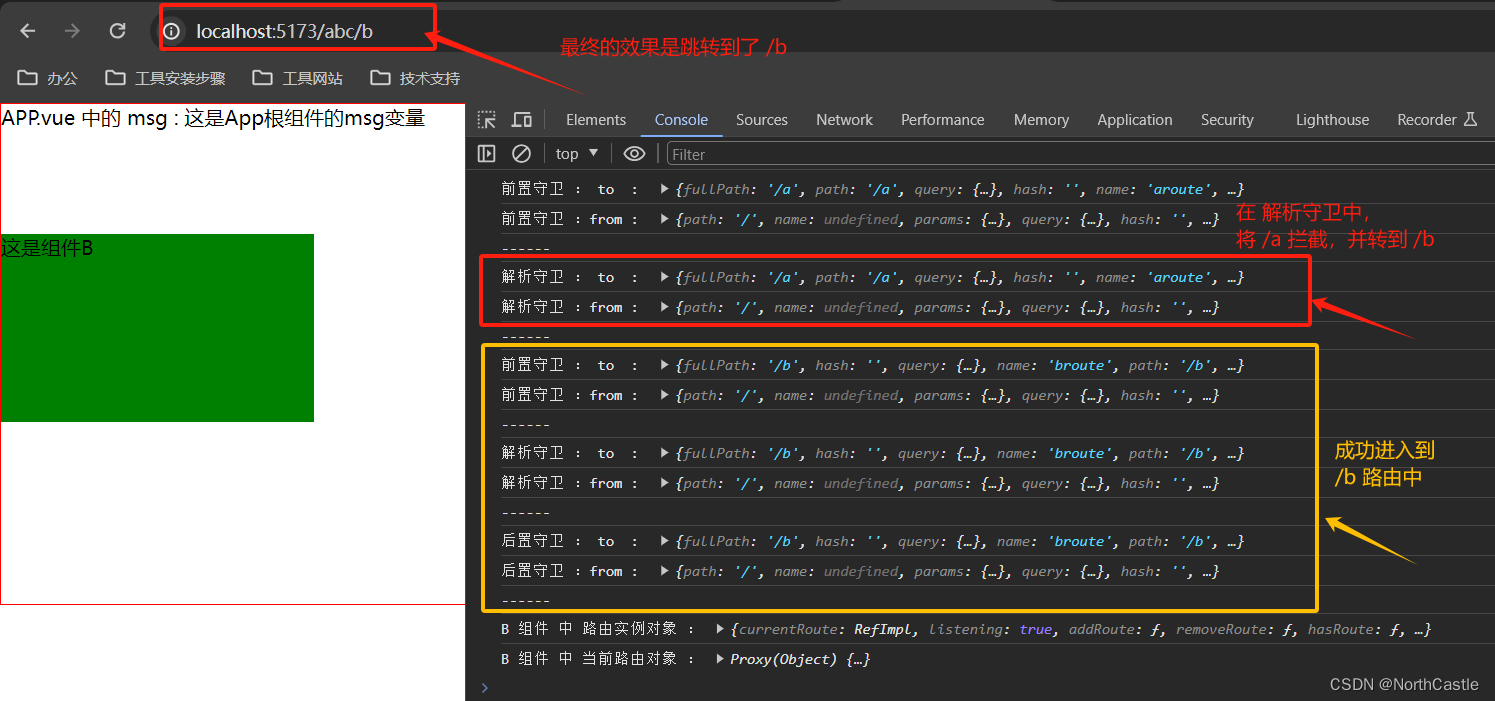
Vue3-35-路由-路由守卫的简单认识
什么是路由守卫 路由守卫,就是在 路由跳转 的过程中, 可以进行一些拦截,做一些逻辑判断, 控制该路由是否可以正常跳转的函数。常用的路由守卫有三个 : beforeEach() : 前置守卫,在路由 跳转前 就会被拦截&…...
制药企业符合CSV验证需要注意什么?
在制药行业中,计算机化系统验证(CSV)是确保生产过程的合规性和数据完整性的关键要素。通过CSV验证,制药企业可以保证其计算机化系统的可靠性和合规性,从而确保产品质量和患者安全。然而,符合CSV验证并不是一…...

再谈动态SQL
专栏精选 引入Mybatis Mybatis的快速入门 Mybatis的增删改查扩展功能说明 mapper映射的参数和结果 Mybatis复杂类型的结果映射 Mybatis基于注解的结果映射 Mybatis枚举类型处理和类型处理器 再谈动态SQL Mybatis配置入门 Mybatis行为配置之Ⅰ—缓存 Mybatis行为配置…...
【数据结构】树
一.二叉树的基本概念和性质: 1.二叉树的递归定义: 二叉树或为空树,或是由一个根结点加上两棵分别称为左子树和右子树的、互不相交的二叉树组成 2.二叉树的特点: (1)每个结点最多只有两棵子树࿰…...
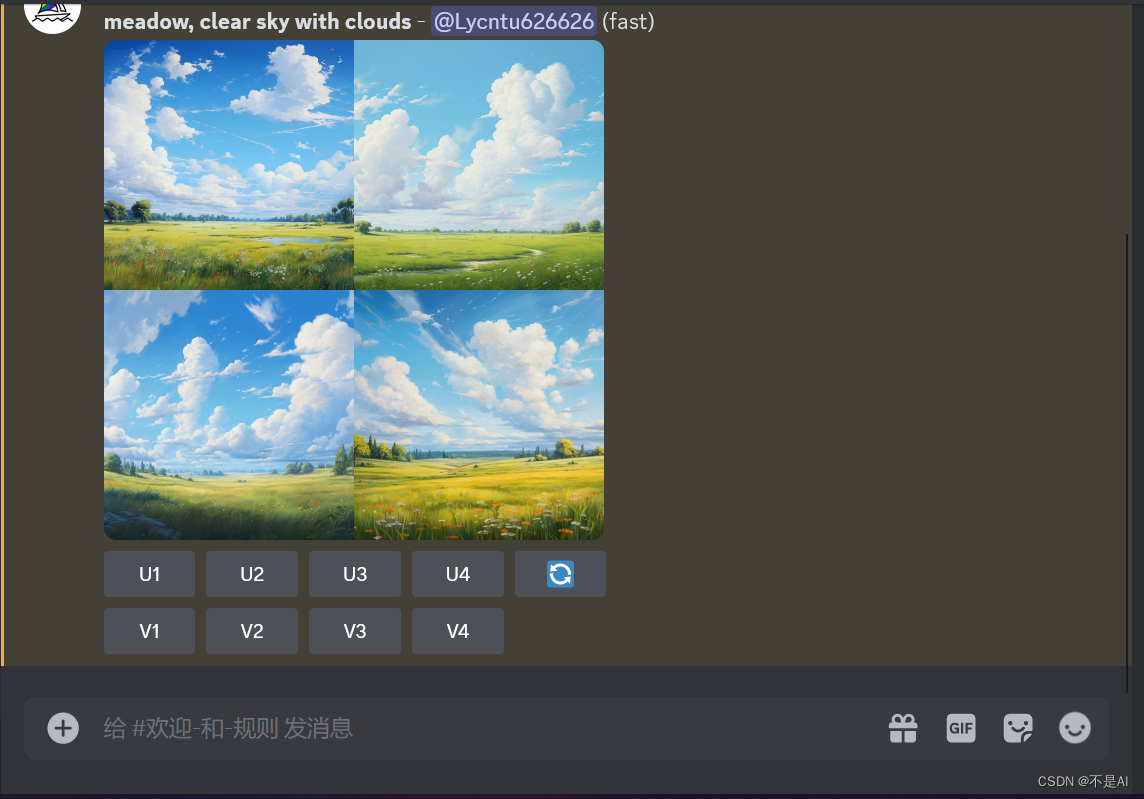
【Midjourney】AI绘画新手教程(一)登录和创建服务器,生成第一幅画作
一、登录Discord 1、访问Discord官网 使用柯學尚网(亲测非必须,可加快响应速度)访问Discord官方网址:https://discord.com 选择“在您的浏览器中打开Discord” 然后,注册帐号、购买套餐等,在此不做缀述。…...

对比 PyTorch 和 TensorFlow:选择适合你的深度学习框架
目录 引言 深度学习在各行业中的应用 PyTorch 和 TensorFlow 简介 PyTorch:简介与设计理念 发展历史和背景 主要特点和设计理念 TensorFlow:简介与设计理念 发展历史和背景 主要特点和设计理念 PyTorch 和 TensorFlow 的重要性 Pytorch对比Te…...

Oracle笔记-查看表已使用空间最大空间
目前以Oracle18c为例,主要是查这个表USER_SEGMENTS。 在 Oracle 18c 数据库中,USER_SEGMENTS 是一个系统表,用于存储当前用户(当前会话)拥有的所有段的信息。段是 Oracle 中分配存储空间的逻辑单位,用于存…...

大数据HCIE成神之路之特征工程——特征选择
特征选择 1.1 特征选择 - Filter方法1.1.1 实验任务1.1.1.1 实验背景1.1.1.2 实验目标1.1.1.3 实验数据解析1.1.1.4 实验思路 1.1.2 实验操作步骤 1.2 特征选择 - Wrapper方法1.2.1 实验任务1.2.1.1 实验背景1.2.1.2 实验目标1.2.1.3 实验数据解析1.2.1.4 实验思路 1.2.2 实验操…...

python 正则-常见题目
1、邮箱 print(re.findall(r[\w-][\w-]\.[\w-], weidianqq.com))2、身份证号 xxxxxx yyyy MM dd 375 0 十八位 print(re.findall(r(?:18|19|(?:[23]\d))\d{2}, 2010)) # 年print(re.findall(r(?:0[1-9])|10|11|12, 11)) # 月print(re.findall(r(?:[0-2][1-9])|10|20|30|3…...

解析:Eureka的工作原理
Eureka是Netflix开源的一个基于REST的的服务发现注册框架,它遵循了REST协议,提供了一套简单的API来完成服务的注册和发现。Eureka能够帮助分布式系统中的服务提供者自动将自身注册到注册中心,同时也能够让服务消费者从注册中心发现服务提供者…...

RecyclerView 与 ListView 区别和使用
前置知识:ListView基本用法与性能提升 RecyclerView 与 ListView 区别 RecyclerView 需要设置布局(LinearLayoutManager、GridLayoutManager、StaggeredGridLayoutManager) recyclerView?.layoutManager LinearLayoutManager(activity) …...

力扣232. 用栈实现队列
题目 请你仅使用两个栈实现先入先出队列。队列应当支持一般队列支持的所有操作(push、pop、peek、empty): 实现 MyQueue 类: void push(int x) 将元素 x 推到队列的末尾int pop() 从队列的开头移除并返回元素int peek() 返回队列开…...

Unity3D中Gfx.WaitForPresent优化方案
前言 在Unity中,Gfx.WaitForPresent占用CPU过高通常表示主线程在等待GPU完成渲染(即CPU被阻塞),这表明存在GPU瓶颈或垂直同步/帧率设置问题。以下是系统的优化方案: 对惹,这里有一个游戏开发交流小组&…...

MongoDB学习和应用(高效的非关系型数据库)
一丶 MongoDB简介 对于社交类软件的功能,我们需要对它的功能特点进行分析: 数据量会随着用户数增大而增大读多写少价值较低非好友看不到其动态信息地理位置的查询… 针对以上特点进行分析各大存储工具: mysql:关系型数据库&am…...

多模态商品数据接口:融合图像、语音与文字的下一代商品详情体验
一、多模态商品数据接口的技术架构 (一)多模态数据融合引擎 跨模态语义对齐 通过Transformer架构实现图像、语音、文字的语义关联。例如,当用户上传一张“蓝色连衣裙”的图片时,接口可自动提取图像中的颜色(RGB值&…...

ETLCloud可能遇到的问题有哪些?常见坑位解析
数据集成平台ETLCloud,主要用于支持数据的抽取(Extract)、转换(Transform)和加载(Load)过程。提供了一个简洁直观的界面,以便用户可以在不同的数据源之间轻松地进行数据迁移和转换。…...

数据库分批入库
今天在工作中,遇到一个问题,就是分批查询的时候,由于批次过大导致出现了一些问题,一下是问题描述和解决方案: 示例: // 假设已有数据列表 dataList 和 PreparedStatement pstmt int batchSize 1000; // …...

CRMEB 框架中 PHP 上传扩展开发:涵盖本地上传及阿里云 OSS、腾讯云 COS、七牛云
目前已有本地上传、阿里云OSS上传、腾讯云COS上传、七牛云上传扩展 扩展入口文件 文件目录 crmeb\services\upload\Upload.php namespace crmeb\services\upload;use crmeb\basic\BaseManager; use think\facade\Config;/*** Class Upload* package crmeb\services\upload* …...

汇编常见指令
汇编常见指令 一、数据传送指令 指令功能示例说明MOV数据传送MOV EAX, 10将立即数 10 送入 EAXMOV [EBX], EAX将 EAX 值存入 EBX 指向的内存LEA加载有效地址LEA EAX, [EBX4]将 EBX4 的地址存入 EAX(不访问内存)XCHG交换数据XCHG EAX, EBX交换 EAX 和 EB…...

CVPR2025重磅突破:AnomalyAny框架实现单样本生成逼真异常数据,破解视觉检测瓶颈!
本文介绍了一种名为AnomalyAny的创新框架,该方法利用Stable Diffusion的强大生成能力,仅需单个正常样本和文本描述,即可生成逼真且多样化的异常样本,有效解决了视觉异常检测中异常样本稀缺的难题,为工业质检、医疗影像…...

【C++】纯虚函数类外可以写实现吗?
1. 答案 先说答案,可以。 2.代码测试 .h头文件 #include <iostream> #include <string>// 抽象基类 class AbstractBase { public:AbstractBase() default;virtual ~AbstractBase() default; // 默认析构函数public:virtual int PureVirtualFunct…...
 Module Federation:Webpack.config.js文件中每个属性的含义解释)
MFE(微前端) Module Federation:Webpack.config.js文件中每个属性的含义解释
以Module Federation 插件详为例,Webpack.config.js它可能的配置和含义如下: 前言 Module Federation 的Webpack.config.js核心配置包括: name filename(定义应用标识) remotes(引用远程模块࿰…...
