【算法数据结构体系篇class12、13】:二叉树
一、判断二叉树是否是完全二叉树
/**
* 判断二叉树是否是完全二叉树
*
* //判断层序遍历过程如果节点有右子树 没有左子树 那么就不是完全二叉树
* //判断层序遍历过程如果遇到第一个节点是没有左或右子树的,也就是只有一个子节点或者没有,那么再往后层序遍历的节点都将是叶子节点,否则就不是完全二叉树
*/
代码演示:
package class12;import java.util.LinkedList;
import java.util.Queue;/*** 判断二叉树是否是完全二叉树* <p>* //判断层序遍历过程如果节点有右子树 没有左子树 那么就不是完全二叉树* //判断层序遍历过程如果遇到第一个节点是没有左或右子树的,也就是只有一个子节点或者没有,那么再往后层序遍历的节点都将是叶子节点,否则就不是完全二叉树*/
public class IsCBT {public static class Node {public int value;public Node left;public Node right;public Node(int data) {this.value = data;}}//方式一: 完全二叉树是从上到下从左到右都是依次有节点//判断层序遍历过程如果节点有右子树 没有左子树 那么就不是完全二叉树//判断层序遍历过程如果遇到第一个节点是没有左或右子树的,也就是只有一个子节点或者没有,那么再往后层序遍历的节点都将是叶子节点,否则就不是完全二叉树public static boolean isCBT1(Node head) {if (head == null) {return true;}//层序遍历二叉树Queue<Node> queue = new LinkedList<>();queue.add(head);//定义一个辅助变量,记录当前弹出队列节点是否只有一个子节点或没有子节点,如果是则赋值true,那么接着下次弹出的节点就肯定是叶子节点,并且没有子节点,这样才符合完全二叉树特性boolean flag = false;while (!queue.isEmpty()) {//弹出队列节点head = queue.poll();//记录当前节点的左右子节点Node left = head.left;Node right = head.right;//判断//如果 flag是true,表示上次弹出的节点的子节点不双全,那么来到当前节点,如果还存在有子节点,就表示节点没有从左到右填充,不是完全二叉树if ((flag && (left != null || right != null))||//或者当前节点 左子节点空,但右子节点非空 也不符合完全二叉树(left == null && right != null)) {//则直接返回falsereturn false;}//接着判断左右子节点,非空则入队列if (left != null) {queue.add(left);}if (right != null) {queue.add(right);}//判断当前弹出节点是否子节点不双全,是的话就需要将falg赋值true 表示如果满足完全二叉树特性的话,后续的都是叶子节点if (left == null || right == null) {flag = true;}}//遍历后如果没有不符合的节点 那么就是完全二叉树,返回truereturn true;}/*** 递归套路模板做法来判断是否十完全二叉树* 1)假设以X节点为头,假设可以向X左树和X右树要任何信息* 2)在上一步的假设下,讨论以X为头节点的树,得到答案的可能性(最重要)* 3)列出所有可能性后,确定到底需要向左树和右树要什么样的信息* 4)把左树信息和右树信息求全集,就是任何一棵子树都需要返回的信息S* 5)递归函数都返回S,每一棵子树都这么要求* 6)写代码,在代码中考虑如何把左树的信息和右树信息整合出整棵树的信息*/public static boolean isCBT2(Node head) {//base case:空树,也定义为完全二叉树 返回trueif (head == null) {return true;}return process(head).isCBT;}//定义节点返回信息,先分析题目,需要判断以head节点的二叉树是否为完全二叉树,那么需要我们判断这四种情况://1.节点左树和右树是满二叉树,并且左树高度=右树高度//2.节点左树是完全二叉树,右数是满二叉树,并且左树高度=右树高度+1//3.节点左树和右树是满二叉树,并且左树高度=右树高度+1//4.节点左树是满二叉树,右树是完全二叉树,并且左树高度=右树高度//符合这四种情况的二叉树,都是完全二叉树 ,从中可以判断,每个节点都需要带三个信息://是否是满二叉树,是否是完全二叉树,高度 接着利用 二叉树 后序遍历 左右根的递归序,//这样才能满足从下往上返回给上节点信息。public static class Info {public boolean isFull;public boolean isCBT;public int height;public Info(boolean full, boolean cbt, int h) {isFull = full;isCBT = cbt;height = h;}}//定义递归程序,最终返回节点信息,主函数调用返回isCBT属性值public static Info process(Node head) {if (head == null) {//base case: 当递归到空节点的时候,即返回空树的信息,是满二叉树、是完全二叉树、高度0return new Info(true, true, 0);}//后序遍历 分别取左树 右树的信息Info leftInfo = process(head.left);Info rightInfo = process(head.right);//接着将当前节点的三个信息返回给上层节点isFull isCBT height 最后return封装到信息类//高度的获取,当前节点高度,就是其左树与右树最大高度树+当前节点+int height = Math.max(leftInfo.height, rightInfo.height) + 1;//是否满二叉树,就是判断左树与右树是否是满二叉树,以及两子树高度相等boolean isFull = leftInfo.isFull && rightInfo.isFull && leftInfo.height == rightInfo.height;//是否完全二叉树,在前面分析有四种情况,符合其中一种就是完全二叉树,初始值可以赋值false,符合再符合trueboolean isCBT = false;if (isFull) {//情况1:1.节点左树和右树是满二叉树,并且左树高度=右树高度 其实就是判断是否是满二叉树,直接引用前面的isFull的判断即可isCBT = true;} else if (leftInfo.isCBT && rightInfo.isFull && leftInfo.height == rightInfo.height + 1) {//2.节点左树是完全二叉树,右数是满二叉树,并且左树高度=右树高度+1isCBT = true;} else if(leftInfo.isFull && rightInfo.isFull && leftInfo.height == rightInfo.height+1){//3.节点左树和右树是满二叉树,并且左树高度=右树高度+1isCBT = true;}else if(leftInfo.isFull && rightInfo.isCBT && leftInfo.height == rightInfo.height){//4.节点左树是满二叉树,右树是完全二叉树,并且左树高度=右树高度isCBT = true;}//最后将当前节点信息返回给上层节点return new Info(isFull,isCBT,height);}// for testpublic static Node generateRandomBST(int maxLevel, int maxValue) {return generate(1, maxLevel, maxValue);}// for testpublic static Node generate(int level, int maxLevel, int maxValue) {if (level > maxLevel || Math.random() < 0.5) {return null;}Node head = new Node((int) (Math.random() * maxValue));head.left = generate(level + 1, maxLevel, maxValue);head.right = generate(level + 1, maxLevel, maxValue);return head;}public static void main(String[] args) {int maxLevel = 5;int maxValue = 100;int testTimes = 1000000;for (int i = 0; i < testTimes; i++) {Node head = generateRandomBST(maxLevel, maxValue);if (isCBT1(head) != isCBT2(head)) {System.out.println("Oops!");}}System.out.println("finish!");}
}
二、二叉树的递归套路
1)假设以X节点为头,假设可以向X左树和X右树要任何信息
2)在上一步的假设下,讨论以X为头节点的树,得到答案的可能性(最重要)
3)列出所有可能性后,确定到底需要向左树和右树要什么样的信息
4)把左树信息和右树信息求全集,就是任何一棵子树都需要返回的信息S
5)递归函数都返回S,每一棵子树都这么要求
6)写代码,在代码中考虑如何把左树的信息和右树信息整合出整棵树的信息
三、判断二叉树是否是搜索二叉树
/**
* 判断二叉树是否是搜索二叉树 中序遍历的节点大小是从小到大的顺序
* 1.左右子树是否为二叉搜索树 2.左子树的最大值要小于当前节点,右子树的最小值要大于当前节点
*
*/
package class12;import java.util.ArrayList;/*** 判断二叉树是否是搜索二叉树 中序遍历的节点大小是从小到大的顺序* 1.左右子树是否为二叉搜索树 2.左子树的最大值要小于当前节点,右子树的最小值要大于当前节点**/
public class IsBST {public static class Node {public int value;public Node left;public Node right;public Node(int data) {this.value = data;}}public static boolean isBST1(Node head) {if (head == null) {return true;}ArrayList<Node> arr = new ArrayList<>();in(head, arr);for (int i = 1; i < arr.size(); i++) {if (arr.get(i).value <= arr.get(i - 1).value) {return false;}}return true;}public static void in(Node head, ArrayList<Node> arr) {if (head == null) {return;}in(head.left, arr);arr.add(head);in(head.right, arr);}public static boolean isBST2(Node head) {if (head == null) {return true;}return process(head).isBST;}//节点返回信息,判断是否为二叉搜索树,就是判断// 1.左右子树是否为二叉搜索树 2.左子树的最大值要小于当前节点,右子树的最小值要大于当前节点//所以我们定义每个节点都同等返回 是否二叉搜索树、最大最小值public static class Info {public boolean isBST;public int max;public int min;public Info(boolean i,int ma, int mi){isBST = i;max = ma;min = mi;}}public static Info process(Node head){//节点空,空树,不好判断最大最小值,所以我们可以返回给上层节点处理。这里就直接返回null,上层判断时//就需要注意判断空情况if(head == null){return null;}//后序遍历,因为要把下层节点都判断好是否为二叉搜索树,再返回给根节点,所以需要左右根的顺序Info leftInfo = process(head.left);Info rightInfo = process(head.right);//定义信息三个属性值 最大最小值默认当前节点值,然后根据左右子树的最大最小值来刷新int max = head.value;int min = head.value;//如果左右子树非空,各自都判断下最大最小值刷新值,需要判空是因为前面空树情况我们返回null,避免空指针需要判空,如果空就不用比较大小if(leftInfo != null ){max = Math.max(max,leftInfo.max);min = Math.min(min,leftInfo.min);}if(rightInfo != null ){max = Math.max(max,rightInfo.max);min = Math.min(min,rightInfo.min);}//判断是否是二叉搜索树 默认给trueboolean isBST = true;//情况1:左树非空,并且左树不是二叉搜索树,则当前节点树就不是二叉搜索树if(leftInfo != null && !leftInfo.isBST){isBST = false;}//情况2:右树非空,并且右树不是二叉搜索树,则当前节点树就不是二叉搜索树if(rightInfo != null && !rightInfo.isBST){isBST = false;}//3.左树非空,并且左树最大值大于等于当前节点 falseif(leftInfo != null && leftInfo.max >= head.value){isBST = false;}//4.右树非空,并且右树最小值小于等于当前节点 falseif(rightInfo != null && rightInfo.min <= head.value){isBST = false;}return new Info(isBST,max,min);}// for testpublic static Node generateRandomBST(int maxLevel, int maxValue) {return generate(1, maxLevel, maxValue);}// for testpublic static Node generate(int level, int maxLevel, int maxValue) {if (level > maxLevel || Math.random() < 0.5) {return null;}Node head = new Node((int) (Math.random() * maxValue));head.left = generate(level + 1, maxLevel, maxValue);head.right = generate(level + 1, maxLevel, maxValue);return head;}public static void main(String[] args) {int maxLevel = 4;int maxValue = 100;int testTimes = 1000000;for (int i = 0; i < testTimes; i++) {Node head = generateRandomBST(maxLevel, maxValue);if (isBST1(head) != isBST2(head)) {System.out.println("Oops!");}}System.out.println("finish!");}}
四、给定一棵二叉树的头节点head,返回这颗二叉树是不是平衡二叉树
/**
* 给定一棵二叉树的头节点head,返回这颗二叉树是不是平衡二叉树
*
* 1.左右树平衡 2.左右树高度差不超过1
*/
package class12;/*** 给定一棵二叉树的头节点head,返回这颗二叉树是不是平衡二叉树** 1.左右树平衡 2.左右树高度差不超过1*/
public class IsBalanced {public static class Node {public int value;public Node left;public Node right;public Node(int data) {this.value = data;}}public static boolean isBalanced1(Node head) {boolean[] ans = new boolean[1];ans[0] = true;process1(head, ans);return ans[0];}public static int process1(Node head, boolean[] ans) {if (!ans[0] || head == null) {return -1;}int leftHeight = process1(head.left, ans);int rightHeight = process1(head.right, ans);if (Math.abs(leftHeight - rightHeight) > 1) {ans[0] = false;}return Math.max(leftHeight, rightHeight) + 1;}public static boolean isBalanced2(Node head) {return process(head).isBalanced;}//二叉树返回节点信息,是否是平衡,需要判断左右树是否平衡,以及左右树高度,返回节点高度差不大于1,是平衡,则节点就是平衡树public static class Info {public boolean isBalanced;public int height;public Info(boolean isb, int h) {isBalanced = isb;height = h;}}//递归树程序,返回头节点的节点信息public static Info process(Node head) {if (head == null) {return new Info(true, 0);}//后序遍历左右根,分别取左右树的节点信息返回当前节点Info leftInfo = process(head.left);Info rightInfo = process(head.right);//定义当前节点的信息,用于返回//高度,左右树最高的子树高度加自身节点高度1int height = Math.max(leftInfo.height, rightInfo.height) + 1;//初始定义是平衡树boolean isBalanced = true;//情况1:如果左右树任意一个不是平衡树 那么这个节点树也就不是平衡树if (!leftInfo.isBalanced || !rightInfo.isBalanced) {isBalanced = false;}//情况2:左右树是平衡树,高度差大于1 那么这个节点树就不是平衡树//情况1已经判断是否平衡子树,所以这里可以省略,能进判断说明肯定没进前面的判断,是平衡子树if (Math.abs(leftInfo.height - rightInfo.height) > 1) {isBalanced = false;}return new Info(isBalanced, height);}// for testpublic static Node generateRandomBST(int maxLevel, int maxValue) {return generate(1, maxLevel, maxValue);}// for testpublic static Node generate(int level, int maxLevel, int maxValue) {if (level > maxLevel || Math.random() < 0.5) {return null;}Node head = new Node((int) (Math.random() * maxValue));head.left = generate(level + 1, maxLevel, maxValue);head.right = generate(level + 1, maxLevel, maxValue);return head;}public static void main(String[] args) {int maxLevel = 5;int maxValue = 100;int testTimes = 1000000;for (int i = 0; i < testTimes; i++) {Node head = generateRandomBST(maxLevel, maxValue);if (isBalanced1(head) != isBalanced2(head)) {System.out.println("Oops!");}}System.out.println("finish!");}}五、给定一棵二叉树的头节点head,返回这颗二叉树是不是满二叉树
/**
* 给定一棵二叉树的头节点head,返回这颗二叉树是不是满二叉树
* 方法一: 1. (2 ^ 层数 ) -1 = 树节点个数
* 方法二: 1.是否左右子树是满二叉树 并且左右树高度相等
*/
package class12;/*** 给定一棵二叉树的头节点head,返回这颗二叉树是不是满二叉树* 方法一: 1. (2 ^ 层数 ) -1 = 树节点个数* 方法二: 1.是否左右子树是满二叉树 并且左右树高度相等*/
public class IsFull {public static class Node {public int value;public Node left;public Node right;public Node(int data) {this.value = data;}}// 第一种方法// 收集整棵树的高度h,和节点数n// 只有满二叉树满足 : 2 ^ h - 1 == npublic static boolean isFull1(Node head) {if (head == null) return true;//取出头节点的信息。然后按2 ^ h - 1 == n 判断是否节点数是满二叉树Info1 isAll = process1(head);return (1 << isAll.height) - 1 == isAll.nodes;}public static class Info1 {public int height;public int nodes;public Info1(int h, int n) {height = h;nodes = n;}}public static Info1 process1(Node head) {//空树,则高度和节点都是0if (head == null) {return new Info1(0, 0);}//后序遍历,先取下层左右树的信息返回Info1 leftInfo = process1(head.left);Info1 rightInfo = process1(head.right);//定义当前节点的高度和节点树总个数int height = Math.max(leftInfo.height, rightInfo.height) + 1;int nodes = leftInfo.nodes + rightInfo.nodes + 1;return new Info1(height, nodes);}//方法二:是否左右子树是满二叉树 并且左右树高度相等public static boolean isFull2(Node head) {if (head == null) {return true;}return process2(head).isFull;}public static class Info2 {public boolean isFull;public int height;public Info2(boolean isf, int h) {isFull = isf;height = h;}}public static Info2 process2(Node head) {if (head == null) {return new Info2(true, 0);}//左右树取信息,返回上层节点Info2 leftInfo = process2(head.left);Info2 rightInfo = process2(head.right);//获取当前节点大小。是否满二叉树int height = Math.max(leftInfo.height, rightInfo.height) + 1;boolean isFull = leftInfo.isFull && rightInfo.isFull && leftInfo.height == rightInfo.height;return new Info2(isFull,height);}// for testpublic static Node generateRandomBST(int maxLevel, int maxValue) {return generate(1, maxLevel, maxValue);}// for testpublic static Node generate(int level, int maxLevel, int maxValue) {if (level > maxLevel || Math.random() < 0.5) {return null;}Node head = new Node((int) (Math.random() * maxValue));head.left = generate(level + 1, maxLevel, maxValue);head.right = generate(level + 1, maxLevel, maxValue);return head;}public static void main(String[] args) {int maxLevel = 5;int maxValue = 100;int testTimes = 1000000;System.out.println("测试开始");for (int i = 0; i < testTimes; i++) {Node head = generateRandomBST(maxLevel, maxValue);if (isFull1(head) != isFull2(head)) {System.out.println("出错了!");}}System.out.println("测试结束");}}六、给定一棵二叉树的头节点head,返回这颗二叉树中最大的二叉搜索子树的大小
/**
* 给定一棵二叉树的头节点head,
* 返回这颗二叉树中最大的二叉搜索子树的大小
*
* 目标是以某节点的树上的最大搜索子树
* 分大情况两种:1.该节点的整棵树不是搜索树,即该节点不做头节点 2.该节点的整棵树是搜索树。即该节点做头节点
* 1: 那么结果就是 左右子树中最大的搜索树即为其所求最大搜索子树大小
* 2: 以该节点的树是二叉搜索树:
* ①左子树是二叉搜索树,最大值小于该节点;
* ②右子树是二叉搜索树,最小值大于该节点;
* ③都是二叉搜索树后,则取左右子树的大小求和再将加该节点+1 得到这个最大搜索树大小 返回
*
* 分情况后分析节点是需要哪些数据:
* 1.最大二叉搜索子树的大小
* 2.是否是二叉搜索树
* 3.树的最大值
* 4.树的最小值
* 5.树的大小
*
* 这里可以合并一个信息,就是如果 1==5的情况下,那么就表示该树是二叉搜索树,所以2可以省略掉
*/
package class12;/*** 给定一棵二叉树的头节点head,* 返回这颗二叉树中最大的二叉搜索子树的大小** 目标是以某节点的树上的最大搜索子树* 分大情况两种:1.该节点的整棵树不是搜索树,即该节点不做头节点 2.该节点的整棵树是搜索树。即该节点做头节点* 1: 那么结果就是 左右子树中最大的搜索树即为其所求最大搜索子树大小* 2: 以该节点的树是二叉搜索树:* ①左子树是二叉搜索树,最大值小于该节点;* ②右子树是二叉搜索树,最小值大于该节点;* ③都是二叉搜索树后,则取左右子树的大小求和再将加该节点+1 得到这个最大搜索树大小 返回** 分情况后分析节点是需要哪些数据:* 1.最大二叉搜索子树的大小* 2.是否是二叉搜索树* 3.树的最大值* 4.树的最小值* 5.树的大小** 这里可以合并一个信息,就是如果 1==5的情况下,那么就表示该树是二叉搜索树,所以2可以省略掉*/public class MaxSubBSTSize {// 提交时不要提交这个类public static class TreeNode {public int val;public TreeNode left;public TreeNode right;public TreeNode(int value) {val = value;}}public static int largestBSTSubtree(TreeNode head){//空树返回0if(head == null) return 0;return process(head).maxBSTSubtreeSize;}//根据分析的情况,列出四个节点需要返回的信息public static class Info{public int maxBSTSubtreeSize;public int allSize;public int max;public int min;public Info(int m,int a, int ma, int mi){maxBSTSubtreeSize = m;allSize = a;max = ma;min = mi;}}public static Info process(TreeNode head){if(head == null){//因为节点返回的存在最大最小值,空树的时候不好设置就直接返回null,给到上层处理,并且需要注意要判空再处理,避免空指针异常return null;}//后序遍历,左右根,取左右子树信息返回Info leftInfo = process(head.left);Info rightInfo = process(head.right);//返回当前节点的四个信息, 最大子树大小比较复杂需要判断再赋值int max = head.val;int min = head.val;int allSize = 1;//根据左右子树非空来依次刷新当前节点的三个值if (leftInfo != null){max = Math.max(max,leftInfo.max);min = Math.min(min, leftInfo.min);allSize += leftInfo.allSize;}if (rightInfo != null){max = Math.max(max,rightInfo.max);min = Math.min(min, rightInfo.min);allSize += rightInfo.allSize;}//接着判断几种情况,分别比较其大小,取最大的二叉搜索子树大小返回int p1 = -1;//情况1:当前节点整棵树不是二叉搜索树,且左子树非空,那么就返回该左子树的最大二叉搜索子树大小if(leftInfo != null ){p1 = leftInfo.maxBSTSubtreeSize;}int p2 =-1;//情况2:当前节点整棵树不是二叉搜索树,且右子树非空,那么就返回该右子树的最大二叉搜索子树大小if(rightInfo != null ){p2 = rightInfo.maxBSTSubtreeSize;}int p3 = -1;//情况3:当前节点整棵树是二叉搜索树,进行判断//先判断左右子树是否是二叉搜索树//如果树空,空树也是二叉搜索树返回true,非空则判断是否是二叉搜索树,前面提到如果最大搜索子树大小=当前树大小,就说明是二叉搜索树boolean leftBST = leftInfo == null ? true : (leftInfo.maxBSTSubtreeSize == leftInfo.allSize);boolean rightBST = rightInfo == null ? true : (rightInfo.maxBSTSubtreeSize == rightInfo.allSize);if(leftBST && rightBST){//如果左右子树都是二叉搜索树,就判断整个树是否是二叉搜索树 注意判空,则直接true;非空,左树最大值小于当前节点,右树最小值大于当前节点boolean leftMaxLessX = leftInfo == null ? true : (leftInfo.max < head.val);boolean rightMinMoreX = rightInfo == null ? true : (rightInfo.min > head.val);if(leftMaxLessX && rightMinMoreX){//符合的话,那么就表示当前树是二叉搜索树,刷新p3值大小,注意判空,空则返回0,非空 就等于左右子树的allSize求和+1int leftSize = leftInfo == null ? 0 : leftInfo.allSize;int rightSize = rightInfo == null ? 0 : rightInfo.allSize;//当前节点为二叉搜索树,那么最大二叉搜索子树就是自己,大小就是左右树大小求和+自身1p3 = leftSize + rightSize +1;}}//最后比较三种情况的二叉搜索子树的大小,取最大返回return new Info(Math.max(p1, Math.max(p2,p3)),allSize,max,min);}}
七、给定一棵二叉树的头节点head,任何两个节点之间都存在距离,返回整棵二叉树的最大距离
/**
* 给定一棵二叉树的头节点head,任何两个节点之间都存在距离,表示经过多少个节点 也就是树高
* 返回整棵二叉树的最大距离
*
* 1.最大距离没有经过头节点head
* 取左树中最大距离 右树中最大距离
*
* 2.最大距离经过头节点head
* 取左树最远节点到头节点高度,即左树高度 + 右树最远节点到头节点高度,即右树高度 再加头节点 +1
*
* 取其中最大值返回
*/
package class12;import java.util.ArrayList;
import java.util.HashMap;
import java.util.HashSet;/*** 给定一棵二叉树的头节点head,任何两个节点之间都存在距离,表示经过多少个节点 也就是树高* 返回整棵二叉树的最大距离** 1.最大距离没有经过头节点head* 取左树中最大距离 右树中最大距离** 2.最大距离经过头节点head* 取左树最远节点到头节点高度,即左树高度 + 右树最远节点到头节点高度,即右树高度 再加头节点 +1** 取其中最大值返回*/
public class MaxDistance {public static class Node {public int value;public Node left;public Node right;public Node(int data) {this.value = data;}}public static int maxDistance1(Node head) {if (head == null) {return 0;}ArrayList<Node> arr = getPrelist(head);HashMap<Node, Node> parentMap = getParentMap(head);int max = 0;for (int i = 0; i < arr.size(); i++) {for (int j = i; j < arr.size(); j++) {max = Math.max(max, distance(parentMap, arr.get(i), arr.get(j)));}}return max;}public static ArrayList<Node> getPrelist(Node head) {ArrayList<Node> arr = new ArrayList<>();fillPrelist(head, arr);return arr;}public static void fillPrelist(Node head, ArrayList<Node> arr) {if (head == null) {return;}arr.add(head);fillPrelist(head.left, arr);fillPrelist(head.right, arr);}public static HashMap<Node, Node> getParentMap(Node head) {HashMap<Node, Node> map = new HashMap<>();map.put(head, null);fillParentMap(head, map);return map;}public static void fillParentMap(Node head, HashMap<Node, Node> parentMap) {if (head.left != null) {parentMap.put(head.left, head);fillParentMap(head.left, parentMap);}if (head.right != null) {parentMap.put(head.right, head);fillParentMap(head.right, parentMap);}}public static int distance(HashMap<Node, Node> parentMap, Node o1, Node o2) {HashSet<Node> o1Set = new HashSet<>();Node cur = o1;o1Set.add(cur);while (parentMap.get(cur) != null) {cur = parentMap.get(cur);o1Set.add(cur);}cur = o2;while (!o1Set.contains(cur)) {cur = parentMap.get(cur);}Node lowestAncestor = cur;cur = o1;int distance1 = 1;while (cur != lowestAncestor) {cur = parentMap.get(cur);distance1++;}cur = o2;int distance2 = 1;while (cur != lowestAncestor) {cur = parentMap.get(cur);distance2++;}return distance1 + distance2 - 1;}public static int maxDistance2(Node head){if(head == null) return 0;return process(head).maxDistance;}//返回节点信息,需要有最大距离和高度,返回上节点public static class Info{public int maxDistance;public int height;public Info(int m, int h){maxDistance = m;height = h;}}public static Info process(Node head){if(head == null){//空树,那么直接返回最大距离和高度都是0return new Info(0,0);}//后序遍历,取左右节点信息返回当前节点使用Info leftInfo = process(head.left);Info rightInfo = process(head.right);//获取当前节点的高度信息和最大距离,最大距离需要分情况判断后比较大小返回最大int height = Math.max(leftInfo.height,rightInfo.height)+1;//最大距离,分三种情况//情况1:最大距离没经过当前节点,取左树最大距离int p1 = leftInfo.maxDistance;//情况2:最大距离没经过当前节点,取右树最大距离int p2 = rightInfo.maxDistance;//情况3:最大距离经过当前节点,取左树高度+右树高度+当前节点1int p3 = leftInfo.height + rightInfo.height + 1;return new Info(Math.max(p1, Math.max(p2,p3)),height);}// for testpublic static Node generateRandomBST(int maxLevel, int maxValue) {return generate(1, maxLevel, maxValue);}// for testpublic static Node generate(int level, int maxLevel, int maxValue) {if (level > maxLevel || Math.random() < 0.5) {return null;}Node head = new Node((int) (Math.random() * maxValue));head.left = generate(level + 1, maxLevel, maxValue);head.right = generate(level + 1, maxLevel, maxValue);return head;}public static void main(String[] args) {int maxLevel = 4;int maxValue = 100;int testTimes = 1000000;for (int i = 0; i < testTimes; i++) {Node head = generateRandomBST(maxLevel, maxValue);if (maxDistance1(head) != maxDistance2(head)) {System.out.println("Oops!");}}System.out.println("finish!");}
}
八、给定一棵二叉树的头节点head,返回这颗二叉树中最大的二叉搜索子树的头节点
package class13;import java.util.ArrayList;/*** 给定一棵二叉树的头节点head,* 返回这颗二叉树中最大的二叉搜索子树的头节点*/
public class MaxSubBSTHead {public static class Node {public int value;public Node left;public Node right;public Node(int data) {this.value = data;}}public static int getBSTSize(Node head) {if (head == null) {return 0;}ArrayList<Node> arr = new ArrayList<>();in(head, arr);for (int i = 1; i < arr.size(); i++) {if (arr.get(i).value <= arr.get(i - 1).value) {return 0;}}return arr.size();}public static void in(Node head, ArrayList<Node> arr) {if (head == null) {return;}in(head.left, arr);arr.add(head);in(head.right, arr);}public static Node maxSubBSTHead1(Node head) {if (head == null) {return null;}if (getBSTSize(head) != 0) {return head;}Node leftAns = maxSubBSTHead1(head.left);Node rightAns = maxSubBSTHead1(head.right);return getBSTSize(leftAns) >= getBSTSize(rightAns) ? leftAns : rightAns;}public static Node maxSubBSTHead2(Node head) {if (head == null) return null;return process(head).maxSubBSTHead;}//返回节点信息public static class Info {public Node maxSubBSTHead;public int maxSubBSTSize;public int max;public int min;public Info(Node ma, int size, int m, int mi) {maxSubBSTHead = ma;maxSubBSTSize = size;max = m;min = mi;}}public static Info process(Node head) {if (head == null) {//空树,不好判断最大最小值,就返回空,返回给上层节点处理。需要注意判空处理return null;}//后序遍历,获取左右子树信息Info leftInfo = process(head.left);Info rightInfo = process(head.right);//定义当前节点属性信息int max = head.value;int min = head.value;Node maxSubBSTHead = null;int maxSubBSTSize = 0;//左右树不空,刷新属性信息。// 两种情况1 2:同步按 左右子树其一是最大二叉搜索树的两种情况进行赋值maxSubBSTHeadif (leftInfo != null) {max = Math.max(max, leftInfo.max);min = Math.min(min, leftInfo.min);//左树非空,先定义最大二叉搜索树头节点和大小是其左树的值maxSubBSTHead = leftInfo.maxSubBSTHead;maxSubBSTSize = leftInfo.maxSubBSTSize;}if (rightInfo != null) {max = Math.max(max, rightInfo.max);min = Math.min(min, rightInfo.min);//刷新最大头节点,前提是如果右树的大小是大于左树的 再重新赋值if (rightInfo.maxSubBSTSize > maxSubBSTSize) {maxSubBSTHead = rightInfo.maxSubBSTHead;maxSubBSTSize = rightInfo.maxSubBSTSize;}}//情况3 当前节点树是最大二叉搜索树,返回该节点//判断子树是否空,空则为二叉搜索树返回true 非空则判断 子树最大二叉搜索树头节点是否对应当前节点树的子节点,并且符合左树最大值小于当前节点,右树最小值大于当前节点if ((leftInfo == null || (leftInfo.maxSubBSTHead == head.left && leftInfo.max < head.value))&& (rightInfo == null || (rightInfo.maxSubBSTHead == head.right && rightInfo.min > head.value))) {//符合则刷新最大二叉搜索树节点和大小 大小就是左右树大小和+1maxSubBSTHead = head;maxSubBSTSize = (leftInfo == null ? 0 : leftInfo.maxSubBSTSize) + (rightInfo == null ? 0 : rightInfo.maxSubBSTSize) + 1;}return new Info(maxSubBSTHead,maxSubBSTSize,max,min);}// for testpublic static Node generateRandomBST(int maxLevel, int maxValue) {return generate(1, maxLevel, maxValue);}// for testpublic static Node generate(int level, int maxLevel, int maxValue) {if (level > maxLevel || Math.random() < 0.5) {return null;}Node head = new Node((int) (Math.random() * maxValue));head.left = generate(level + 1, maxLevel, maxValue);head.right = generate(level + 1, maxLevel, maxValue);return head;}public static void main(String[] args) {int maxLevel = 4;int maxValue = 100;int testTimes = 1000000;for (int i = 0; i < testTimes; i++) {Node head = generateRandomBST(maxLevel, maxValue);if (maxSubBSTHead1(head) != maxSubBSTHead2(head)) {System.out.println("Oops!");}}System.out.println("finish!");}
}
九、给定一棵二叉树的头节点head,和另外两个节点a和b。返回a和b的最低公共祖先
/**
* 给定一棵二叉树的头节点head,和另外两个节点a和b。
* 返回a和b的最低公共祖先
* <p>
* 分析情况:
* 1.最低公共祖先不在head:
* 在左树中找到a b 最低公共祖先,那么将该ans节点往上返回给头节点
* 在右树找到,同理返回上层
* 2.最低公共祖先在head:
* 那么肯定 a b 分别都能在子树中找到
* <p>
* 这里注意找 a b 节点除了在节点的子树找之外,也要判断当前节点是否为a b 可能递归到相等的时候
*/
package class13;import java.util.ArrayList;
import java.util.HashMap;
import java.util.HashSet;/*** 给定一棵二叉树的头节点head,和另外两个节点a和b。* 返回a和b的最低公共祖先* <p>* 分析情况:* 1.最低公共祖先不在head:* 在左树中找到a b 最低公共祖先,那么将该ans节点往上返回给头节点* 在右树找到,同理返回上层* 2.最低公共祖先在head:* 那么肯定 a b 分别都能在子树中找到* <p>* 这里注意找 a b 节点除了在节点的子树找之外,也要判断当前节点是否为a b 可能递归到相等的时候*/public class LowestAncestor {public static class Node {public int value;public Node left;public Node right;public Node(int data) {this.value = data;}}public static Node lowestAncestor1(Node head, Node o1, Node o2) {if (head == null) {return null;}// key的父节点是valueHashMap<Node, Node> parentMap = new HashMap<>();parentMap.put(head, null);fillParentMap(head, parentMap);HashSet<Node> o1Set = new HashSet<>();Node cur = o1;o1Set.add(cur);while (parentMap.get(cur) != null) {cur = parentMap.get(cur);o1Set.add(cur);}cur = o2;while (!o1Set.contains(cur)) {cur = parentMap.get(cur);}return cur;}public static void fillParentMap(Node head, HashMap<Node, Node> parentMap) {if (head.left != null) {parentMap.put(head.left, head);fillParentMap(head.left, parentMap);}if (head.right != null) {parentMap.put(head.right, head);fillParentMap(head.right, parentMap);}}public static Node lowestAncestor2(Node head, Node a, Node b) {if (head == null) return null;return process(head, a, b).ans;}//返回节点的信息:是否找到a b 节点,是否存在最低公共祖先节点public static class Info {public boolean findA;public boolean findB;public Node ans;public Info(boolean a, boolean b, Node an) {findA = a;findB = b;ans = an;}}public static Info process(Node head, Node a, Node b) {if(head == null){//空树,则是不回找到ab节点false,也没有最低祖先nullreturn new Info(false,false,null);}//后序遍历 取左右树信息Info leftInfo = process(head.left,a,b);Info rightInfo = process(head.right,a,b);//给当前节点属性信息赋值返回//判断当前节点是否是ab节点,以及左右子树是否找到了ab节点boolean findA = a == head || leftInfo.findA || rightInfo.findA;boolean findB = b == head || leftInfo.findB || rightInfo.findB;//判断是否是最低祖先。//情况1:不在当前节点 在子树:子树非空,那么就是其最低祖先节点属性Node ans = null;if(leftInfo.ans != null){ans = leftInfo.ans;}else if(rightInfo.ans != null){ans = rightInfo.ans;}//情况2:当前节点是最低祖先,那么就是当前节点树能找到ab节点,返回当前节点else if(findA && findB){ans = head;}return new Info(findA,findB,ans);}// for testpublic static Node generateRandomBST(int maxLevel, int maxValue) {return generate(1, maxLevel, maxValue);}// for testpublic static Node generate(int level, int maxLevel, int maxValue) {if (level > maxLevel || Math.random() < 0.5) {return null;}Node head = new Node((int) (Math.random() * maxValue));head.left = generate(level + 1, maxLevel, maxValue);head.right = generate(level + 1, maxLevel, maxValue);return head;}// for testpublic static Node pickRandomOne(Node head) {if (head == null) {return null;}ArrayList<Node> arr = new ArrayList<>();fillPrelist(head, arr);int randomIndex = (int) (Math.random() * arr.size());return arr.get(randomIndex);}// for testpublic static void fillPrelist(Node head, ArrayList<Node> arr) {if (head == null) {return;}arr.add(head);fillPrelist(head.left, arr);fillPrelist(head.right, arr);}public static void main(String[] args) {int maxLevel = 4;int maxValue = 100;int testTimes = 1000000;for (int i = 0; i < testTimes; i++) {Node head = generateRandomBST(maxLevel, maxValue);Node o1 = pickRandomOne(head);Node o2 = pickRandomOne(head);if (lowestAncestor1(head, o1, o2) != lowestAncestor2(head, o1, o2)) {System.out.println("Oops!");}}System.out.println("finish!");}}
十、派对的最大快乐值
员工信息的定义如下:
class Employee {
public int happy; // 这名员工可以带来的快乐值
List<Employee> subordinates; // 这名员工有哪些直接下级
}
公司的每个员工都符合 Employee 类的描述。整个公司的人员结构可以看作是一棵标准的、没有环的多叉树。树的头节点是公司唯一的老板。除老板之外的每个员工都有唯一的直接上级。 叶节点是没有任何下属的基层员工(subordinates列表为空),除基层员工外,每个员工都有一个或多个直接下级。
这个公司现在要办party,你可以决定哪些员工来,哪些员工不来,规则:
1.如果某个员工来了,那么这个员工的所有直接下级都不能来
2.派对的整体快乐值是所有到场员工快乐值的累加
3.你的目标是让派对的整体快乐值尽量大
给定一棵多叉树的头节点boss,请返回派对的最大快乐值。
* //分情况:
* 1.当前节点来参加: 那么下层节点就都不能参加 快乐值0
* 2.当前节点不来参加: 那么下层节点可参加,可不参加,取两者快乐值最大
package class13;
/*** 派对的最大快乐值** 员工信息的定义如下:* class Employee {* public int happy; // 这名员工可以带来的快乐值* List<Employee> subordinates; // 这名员工有哪些直接下级* }* 派对的最大快乐值* 公司的每个员工都符合 Employee 类的描述。整个公司的人员结构可以看作是一棵标准的、 没有环的多叉树。树的头节点是公司唯一的老板。* 除老板之外的每个员工都有唯一的直接上级。 叶节点是没有任何下属的基层员工(subordinates列表为空),除基层员工外,每个员工都有一个或多个直接下级。* 这个公司现在要办party,你可以决定哪些员工来,哪些员工不来,规则:* 1.如果某个员工来了,那么这个员工的所有直接下级都不能来* 2.派对的整体快乐值是所有到场员工快乐值的累加* 3.你的目标是让派对的整体快乐值尽量大* 给定一棵多叉树的头节点boss,请返回派对的最大快乐值。*** //分情况:* 1.当前节点来参加: 那么下层节点就都不能参加 快乐值0* 2.当前节点不来参加: 那么下层节点可参加,可不参加,取两者快乐值最大*/import java.util.ArrayList;
import java.util.List;public class MaxHappy {public static class Employee {public int happy;public List<Employee> nexts;public Employee(int h) {happy = h;nexts = new ArrayList<>();}}public static int maxHappy1(Employee boss) {if (boss == null) {return 0;}return process1(boss, false);}// 当前来到的节点叫cur,// up表示cur的上级是否来,// 该函数含义:// 如果up为true,表示在cur上级已经确定来,的情况下,cur整棵树能够提供最大的快乐值是多少?// 如果up为false,表示在cur上级已经确定不来,的情况下,cur整棵树能够提供最大的快乐值是多少?public static int process1(Employee cur, boolean up) {if (up) { // 如果cur的上级来的话,cur没得选,只能不来int ans = 0;for (Employee next : cur.nexts) {ans += process1(next, false);}return ans;} else { // 如果cur的上级不来的话,cur可以选,可以来也可以不来int p1 = cur.happy;int p2 = 0;for (Employee next : cur.nexts) {p1 += process1(next, true);p2 += process1(next, false);}return Math.max(p1, p2);}}public static int maxHappy2(Employee boss) {//接收boss节点 参加与不参加的两种情况,再返回最大值Info allInfo = process(boss);return Math.max(allInfo.no,allInfo.yes);}//返回信息,即根节点来的快乐值 不来的快乐值public static class Info{public int no;public int yes;public Info(int n, int y){no = n;yes = y;}}public static Info process(Employee cur){if(cur == null){//空节点,也就是没有员工,那么更没有参加与否的快乐值 0return new Info(0,0);}//设置属性 no 没参加 那么快乐值就是0, yes 参加 快乐值就是自身int no = 0;int yes = cur.happy;for(Employee next:cur.nexts){//多叉树往下递归Info nextInfo = process(next);//刷新no值,如果当前节点no 不参加,那么nextInfo子节点 参加或不参加都可以,所以快乐值取两种情况较大值no += Math.max(nextInfo.no,nextInfo.yes);//刷新yes值,当前节点参加,那么子节点不能参加,快乐值0yes += nextInfo.no;}return new Info(no,yes);}// for testpublic static Employee genarateBoss(int maxLevel, int maxNexts, int maxHappy) {if (Math.random() < 0.02) {return null;}Employee boss = new Employee((int) (Math.random() * (maxHappy + 1)));genarateNexts(boss, 1, maxLevel, maxNexts, maxHappy);return boss;}// for testpublic static void genarateNexts(Employee e, int level, int maxLevel, int maxNexts, int maxHappy) {if (level > maxLevel) {return;}int nextsSize = (int) (Math.random() * (maxNexts + 1));for (int i = 0; i < nextsSize; i++) {Employee next = new Employee((int) (Math.random() * (maxHappy + 1)));e.nexts.add(next);genarateNexts(next, level + 1, maxLevel, maxNexts, maxHappy);}}public static void main(String[] args) {int maxLevel = 4;int maxNexts = 7;int maxHappy = 100;int testTimes = 100000;for (int i = 0; i < testTimes; i++) {Employee boss = genarateBoss(maxLevel, maxNexts, maxHappy);if (maxHappy1(boss) != maxHappy2(boss)) {System.out.println("Oops!");}}System.out.println("finish!");}}
相关文章:

【算法数据结构体系篇class12、13】:二叉树
一、判断二叉树是否是完全二叉树/*** 判断二叉树是否是完全二叉树** //判断层序遍历过程如果节点有右子树 没有左子树 那么就不是完全二叉树* //判断层序遍历过程如果遇到第一个节点是没有左或右子树的,也就是只有一个子节点或者没有,那么再往后层序遍历…...

数字IC手撕代码--联发科(总线访问仲裁)
题目描述当A、B两组的信号请求访问某个模块时,为了保证正确的访问,需要对这些信号进行仲裁。请用Verilog实现一个仲裁器,对两组请求信号进行仲后,要求:协议如图所示,请求方发送req(request&…...

白盒测试复习重点
白盒测试白盒测试之逻辑覆盖法逻辑覆盖用例设计方法1.语句覆盖2.判定覆盖(分支覆盖)3.条件覆盖4.判定条件覆盖5.条件组合覆盖6.路径覆盖白盒测试之基本路径测试法基本路径测试方法的步骤1.根据程序流程图画控制流图2.计算圈复杂度3.导出测试用例4.准备测试用例5.例题白盒测试总…...
学习C++这几个网站足矣
文章目录cppreferencecplusplusquick-bench[C 之父的网站](https://www.stroustrup.com/bs_faq.html)C提案[Cpp Core Guidelines](http://isocpp.github.io/CppCoreGuidelines/CppCoreGuidelines)[C Super-FAQ](https://isocpp.org/faq)[learn c](https://www.learncpp.com/)[A…...
——C语言版)
第十四届蓝桥杯模拟赛(第三期)——C语言版
1.找最小数 问题描述: 请找到一个大于 2022 的最小数,这个数转换成十六进制之后,所有的数位(不含前导 0)都为字母(A 到 F)。 请将这个数的十进制形式作为答案提交。 #include <stdio.h> int main(…...
Flutter Button 实例
大家好,我是 17。 在上篇文章 使用 Flutter Button 介绍了如何修改 button 的样式,本文来具体实践一下。 本文列举一些常用的 button 效果,以便在用到的时候方便使用。因为 ElevatedButton 最常用,所以大多以 ElevatedButton 举…...
好玩的docker项目,盒子刷的海思nas,挂载外接硬盘。qb种子
玩法思路(5条消息) 群晖qb下载,tr辅种_屿兮的博客-CSDN博客_群晖辅种qbittorrent简介及设置_哔哩哔哩_bilibiliqb下载器下载Transmission最好用的BT(PT)下载神器/超简单上手教你在NAS轻松部署/告别简陋三步让你升级全中文最新Web界面(BT下载/PT下载/NAS/…...

RabbitMQ的使用
1.初识MQ1.1.同步和异步通讯微服务间通讯有同步和异步两种方式:同步通讯:就像打电话,需要实时响应。异步通讯:就像发邮件,不需要马上回复。两种方式各有优劣,打电话可以立即得到响应,但是你却不…...
Selenium如何隐藏浏览器页面?
Selenium隐藏浏览器页面 背景 在工作,学习中,我们常常会使用selenium来获取网页上的数据,编完完整程序之后,实现真正意义上的自动化获取,此时我们会发现在运行中往往会弹出浏览器页面,在调试过程中&…...
基于Ant DesignPro Vue实现通过SpringBoot后台加载自定义菜单- 前后端分离
基于Ant DesignPro Vue实现通过SpringBoot后台加载自定义菜单- 前后端分离 本文想基于Ant DesignPro Vue构建的前端SpringBoot实现的后端接口服务,实现前后端分离开发和独立运行,业务场景是登录认证,认证成功后返回该用户相应权限范围内可见的…...
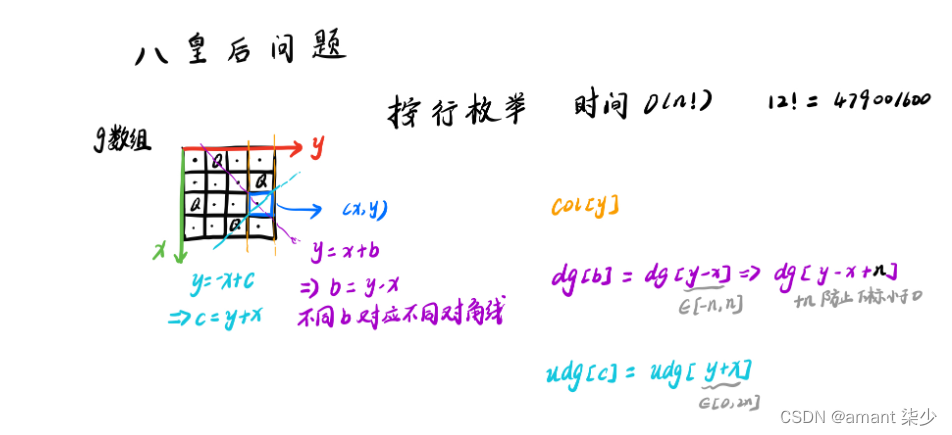
Acwing---843. n-皇后问题
n-皇后问题1.题目2.基本思想3.代码实现1.题目 n−皇后问题是指将 n 个皇后放在 nn 的国际象棋棋盘上,使得皇后不能相互攻击到,即任意两个皇后都不能处于同一行、同一列或同一斜线上。 现在给定整数 n,请你输出所有的满足条件的棋子摆法。 …...

彻底搞清楚内存泄漏的原因,如何避免内存泄漏,如何定位内存泄漏
作为C/C开发人员,内存泄漏是最容易遇到的问题之一,这是由C/C语言的特性引起的。C/C语言与其他语言不同,需要开发者去申请和释放内存,即需要开发者去管理内存,如果内存使用不当,就容易造成段错误(segment fa…...
自动驾驶目标检测项目实战——基于深度学习框架yolov的交通标志检测
自动驾驶目标检测项目实战——基于深度学习框架yolov的交通标志检测 目前目标检测算法有很多,流行的就有faster-rnn和yolov,本文使用了几年前的yolov3框架进行训练,效果还是很好,当然也可以使用更高版本的Yolov进行实战。本代码使…...

flink兼容性验证
flink介绍:https://blog.csdn.net/weixin_43563705/article/details/107604693 一、安装启动 安装flink及其依赖 yum install java-1.8.0-openjdk curl tar mkdir -p /usr/local/flink wget https://mirrors.aliyun.com/apache/flink/flink-1.16.1/flink-1.16.1-bi…...

智慧工厂数字孪生可视化监测系统有效提升厂区安全管控效力
我国制造业正处于产业升级的关键时期,基于数据进行生产策略制定与管理是大势所趋,而数据可视化以更直观的方式成为数据分析传递信息的重要工具。 深圳华锐视点通过三维可视化手段对工厂各类设备进行三维建模,真实复现设备设施外观、结构、运转…...

c++中基本类型详细解释外加基本运算规则
👀👀#c中包括算数类型和空类型。 类型含义wchat_t宽字符bool布尔类型char字符chat16_tunicode字符chat_32unicode字符short短整型int整形long长整型longlong长整型float单精度浮点型double双精度浮点型longdouble扩展精度浮点型 👀…...

扬帆优配“机器人+”方案加码产业发展,这些股有望高增长
“机器人”发明新需求,2022年中国机器人市场规模约为174亿美元。 美国时刻3月1日,特斯拉在得克萨斯州超级工厂举办投资者日活动,展示了人形机器人Optimus的视频,更夸大的是,视频中的机器人好像在制作另一个机器人&…...
推送投票制作微信推送里投票制作教程在线投票活动制作
近些年来,第三方的微信投票制作平台如雨后春笋般络绎不绝。随着手机的互联网的发展及微信开放平台各项基于手机能力的开放,更多人选择微信投票小程序平台,因为它有非常大的优势。1.它比起微信公众号自带的投票系统、传统的H5投票系统有可以图…...
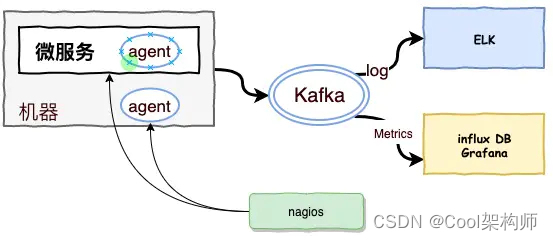
【架构师】跟我一起学架构——微服务分层监控
博客昵称:架构师Cool 最喜欢的座右铭:一以贯之的努力,不得懈怠的人生。 作者简介:一名Coder,软件设计师/鸿蒙高级工程师认证,在备战高级架构师/系统分析师,欢迎关注小弟! 博主小留言…...
Linux:https静态网站搭建案例
目录介绍httpshttps通信过程例介绍https 整个实验是在http实验基础上进行的 因为http协议在传输的时候采用的是明文传输,有安全隐患,所以出现了https(安全套接字层超文本传输协议) HTTPS并不是一个新协议, 而是HTTP…...
)
浏览器访问 AWS ECS 上部署的 Docker 容器(监听 80 端口)
✅ 一、ECS 服务配置 Dockerfile 确保监听 80 端口 EXPOSE 80 CMD ["nginx", "-g", "daemon off;"]或 EXPOSE 80 CMD ["python3", "-m", "http.server", "80"]任务定义(Task Definition&…...

day52 ResNet18 CBAM
在深度学习的旅程中,我们不断探索如何提升模型的性能。今天,我将分享我在 ResNet18 模型中插入 CBAM(Convolutional Block Attention Module)模块,并采用分阶段微调策略的实践过程。通过这个过程,我不仅提升…...

Cinnamon修改面板小工具图标
Cinnamon开始菜单-CSDN博客 设置模块都是做好的,比GNOME简单得多! 在 applet.js 里增加 const Settings imports.ui.settings;this.settings new Settings.AppletSettings(this, HTYMenusonichy, instance_id); this.settings.bind(menu-icon, menu…...

今日科技热点速览
🔥 今日科技热点速览 🎮 任天堂Switch 2 正式发售 任天堂新一代游戏主机 Switch 2 今日正式上线发售,主打更强图形性能与沉浸式体验,支持多模态交互,受到全球玩家热捧 。 🤖 人工智能持续突破 DeepSeek-R1&…...

零基础在实践中学习网络安全-皮卡丘靶场(第九期-Unsafe Fileupload模块)(yakit方式)
本期内容并不是很难,相信大家会学的很愉快,当然对于有后端基础的朋友来说,本期内容更加容易了解,当然没有基础的也别担心,本期内容会详细解释有关内容 本期用到的软件:yakit(因为经过之前好多期…...

深入浅出深度学习基础:从感知机到全连接神经网络的核心原理与应用
文章目录 前言一、感知机 (Perceptron)1.1 基础介绍1.1.1 感知机是什么?1.1.2 感知机的工作原理 1.2 感知机的简单应用:基本逻辑门1.2.1 逻辑与 (Logic AND)1.2.2 逻辑或 (Logic OR)1.2.3 逻辑与非 (Logic NAND) 1.3 感知机的实现1.3.1 简单实现 (基于阈…...

深度学习之模型压缩三驾马车:模型剪枝、模型量化、知识蒸馏
一、引言 在深度学习中,我们训练出的神经网络往往非常庞大(比如像 ResNet、YOLOv8、Vision Transformer),虽然精度很高,但“太重”了,运行起来很慢,占用内存大,不适合部署到手机、摄…...

第一篇:Liunx环境下搭建PaddlePaddle 3.0基础环境(Liunx Centos8.5安装Python3.10+pip3.10)
第一篇:Liunx环境下搭建PaddlePaddle 3.0基础环境(Liunx Centos8.5安装Python3.10pip3.10) 一:前言二:安装编译依赖二:安装Python3.10三:安装PIP3.10四:安装Paddlepaddle基础框架4.1…...

密码学基础——SM4算法
博客主页:christine-rr-CSDN博客 专栏主页:密码学 📌 【今日更新】📌 对称密码算法——SM4 目录 一、国密SM系列算法概述 二、SM4算法 2.1算法背景 2.2算法特点 2.3 基本部件 2.3.1 S盒 2.3.2 非线性变换 编辑…...

如何把工业通信协议转换成http websocket
1.现状 工业通信协议多数工作在边缘设备上,比如:PLC、IOT盒子等。上层业务系统需要根据不同的工业协议做对应开发,当设备上用的是modbus从站时,采集设备数据需要开发modbus主站;当设备上用的是西门子PN协议时…...
