LSTM已死,Transformer当立(LSTM is dead. Long Live Transformers! ):下
2017 年,Google 在论文 Attention is All you need 中提出了 Transformer 模型,其使用 Self-Attention 结构取代了在 NLP 任务中常用的 RNN 网络结构。而且实验也证明Transformer 在效果上已经完败传统的 RNN 网络。Transformer 的整体模型架构如下图所示。尽管它看起来还是很复杂的,但其实我们已经知道了像全连接层(Feed Forward),Softmax层这些基础概念。而在本系列文章的前一篇里(上),我们也解释过了Multi-Head Attention层。 本文将解释搭建Transformer 模型的其它细节。
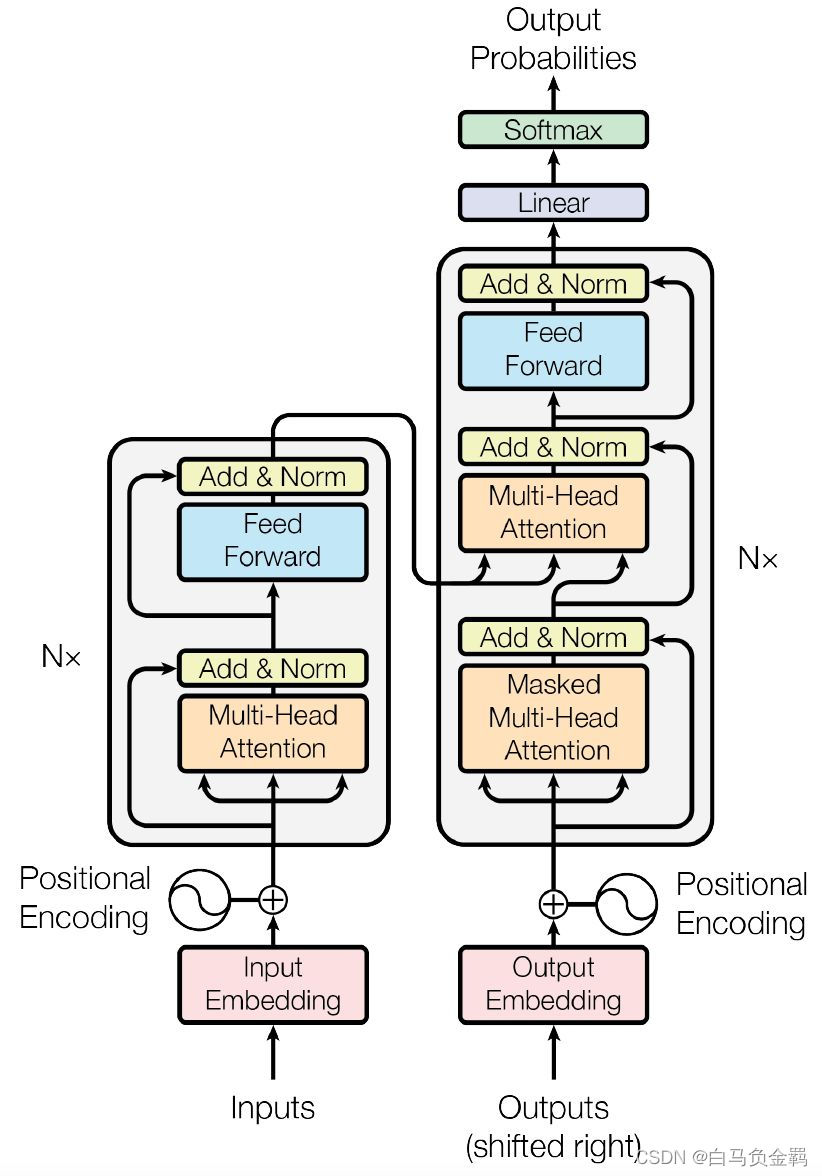
编码组件(上图中作侧部分)由多层编码块(Encoder Block)组成,所以图中使用Nx来表示,在论文中作者使用了 6 层编码器,在实际使用过程中你可以尝试其他层数。
解码组件(上图中右侧部分)也是由相同层数的解码块(Decoder Block)组成(在论文也使用了 6 层),在实际使用过程中你可以尝试其他层数。
本文中部分插图引用自【1】和【2】。
一、编码组件
Transformer 中单词的输入由两部分组成:单词 Embedding 和位置 Embedding (Positional Encoding)。
<
相关文章:

LSTM已死,Transformer当立(LSTM is dead. Long Live Transformers! ):下
2017 年,Google 在论文 Attention is All you need 中提出了 Transformer 模型,其使用 Self-Attention 结构取代了在 NLP 任务中常用的 RNN 网络结构。而且实验也证明Transformer 在效果上已经完败传统的 RNN 网络。Transformer 的整体模型架构如下图所示。尽管它看起来还是很…...
)
OJ万题详解––[NOIP2004 提高组] 合并果子(C++详解)
目录 题目 分析 参考代码 题目 题目描述 一个果园里,多多已经将所有的果子打了下来,而且按果子的不同种类分成了不同的堆。多多决定把所有的果子合成一堆。 每一次合并,多多可以把两堆果子合并到一起,消耗的体力等于两堆果子的…...
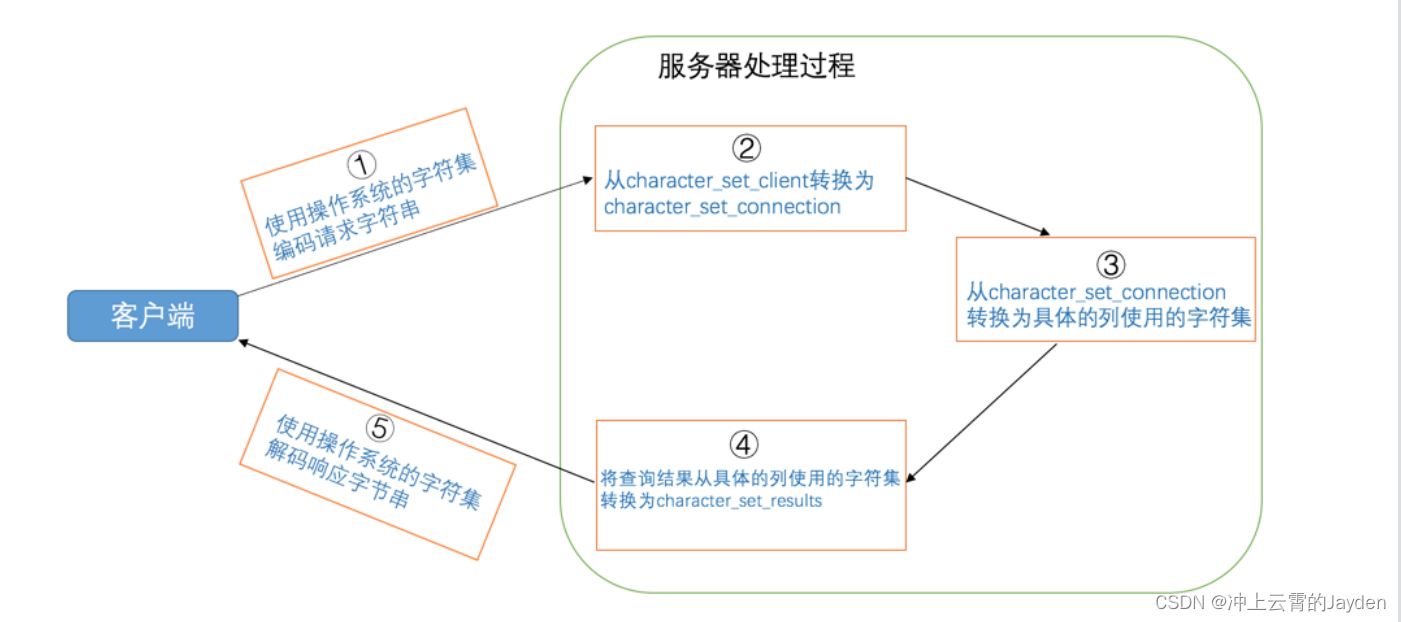
MySQL-字符集和比较规则
在计算机中只能存储二进制数据,那该怎么存储字符串呢?当然是建立字符与二进制数据的映射关系 了,建立这个关系最起码要搞清楚两件事: 界定清楚字符范围:需要把哪些字符映射成二进制数据?编码与解码&#x…...
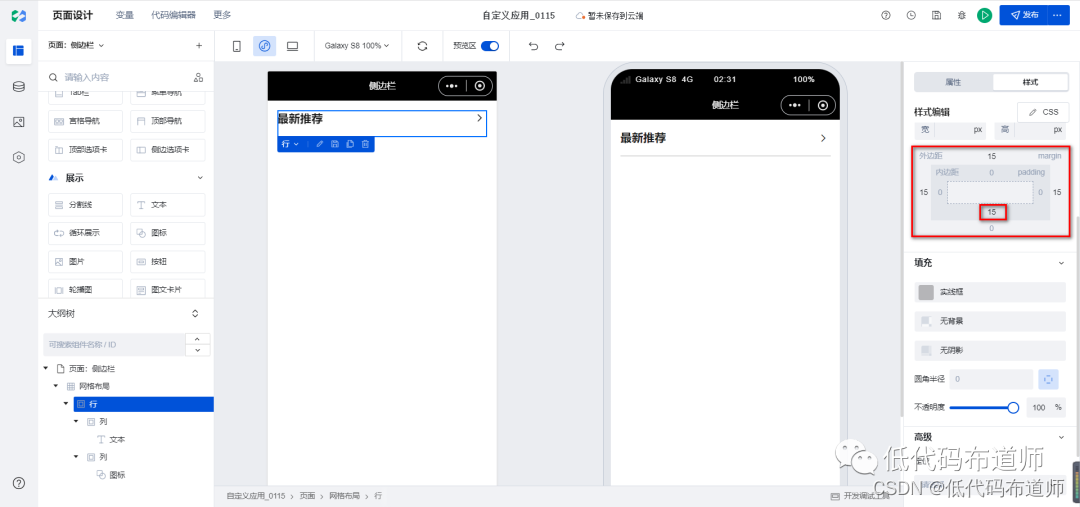
微搭低代码从入门到精通12-网格布局
开发小程序首要的就是考虑布局的问题,我们在以前的版本只能选择普通容器结合图片和文本组件来构建页面。 使用通用组件布局也可以,但有个问题是你要先学习CSS,要懂布局的概念,比如需要知道啥是flex布局,然后还得熟悉每…...
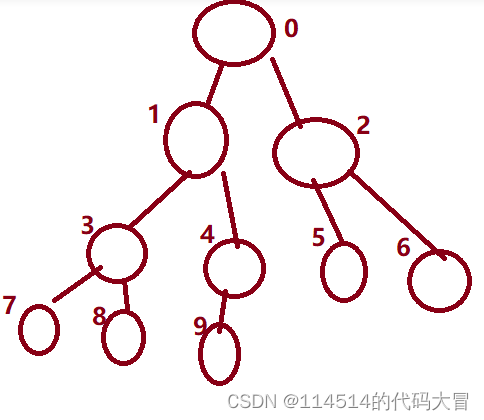
【c语言】二叉树
主页:114514的代码大冒险 qq:2188956112(欢迎小伙伴呀hi✿(。◕ᴗ◕。)✿ ) Gitee:庄嘉豪 (zhuang-jiahaoxxx) - Gitee.com 引入 我们之前已经学过线性数据结构,今天我们将介绍非线性数据结构----树 树是一种非线性的…...
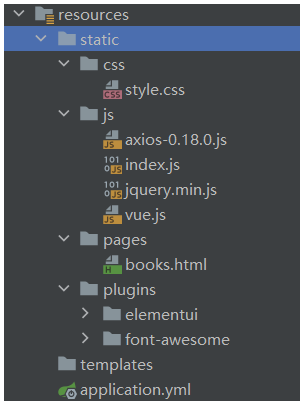
六、Java框架之SpringBoot
黑马课程 文章目录1. SpringBoot入门1.1 SpringBoot入门案例步骤1:创建SpringBoot项目高版本springboot常见错误步骤2:创建BookController步骤3:启动服务器并运行程序pom.xml示例1.2 官网创建SpringBoot1.3 SpringBoot工程快速启动问题导入打…...
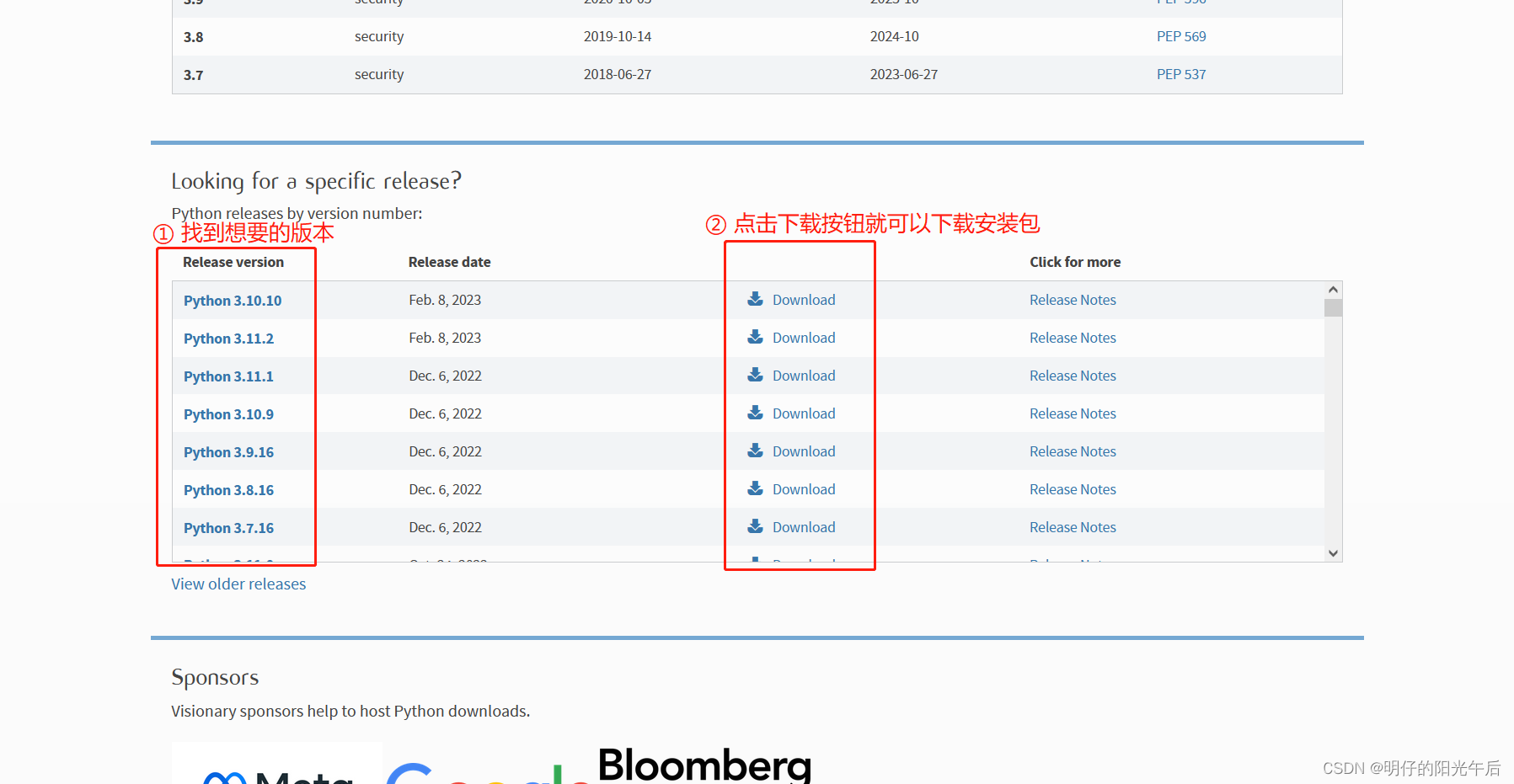
「Python|环境安装|Windows」如何在Windows上安装Python环境?
本文主要介绍如何在Windows上安装Python,帮助初学者或者非程序员伙伴快速搭建可以运行python代码的环境。 文章目录安装python做一点小配置验证python如何安装指定版本的python编程语言的环境搭建一直是学习编程的第一道门槛。 对于如何在Linux系统上安装指定版本的…...

人工智能轨道交通行业周刊-第33期(2023.2.6-2.12)
本期关键词:高铁激光清洗、高铁确认列车、无线通信系统、推理服务优化、量子信息技术 1 整理涉及公众号名单 1.1 行业类 RT轨道交通中关村轨道交通产业服务平台人民铁道世界轨道交通资讯网铁路信号技术交流北京铁路轨道交通网上榜铁路视点ITS World轨道交通联盟V…...
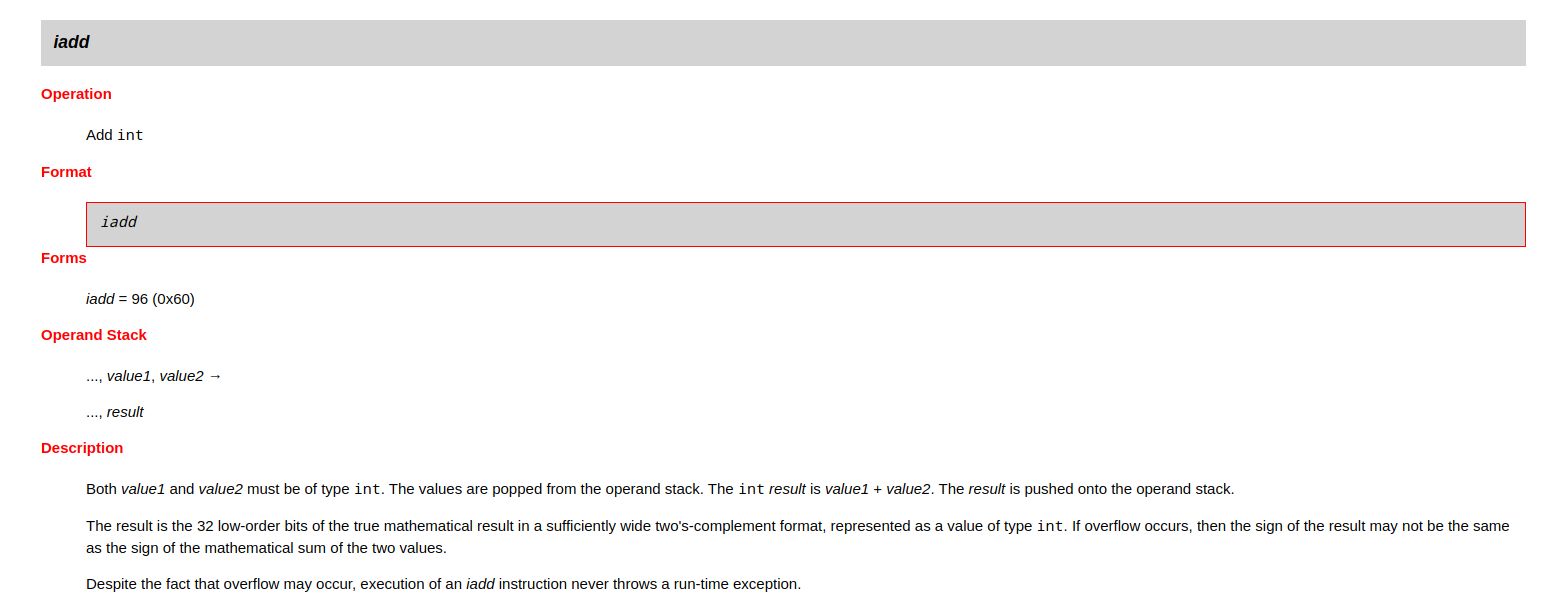
五分钟看懂Java字节码:极简手册
字节码新手很容易被厚厚的 JVM 书籍劝退,即使我看过相关书籍,工作真正用到时也全忘了,还得现学。 等我有了一定的字节码阅读经验,才发现字节码其实非常简单,只需要三步就能快速学会: 先了解 JVM 的基本结…...
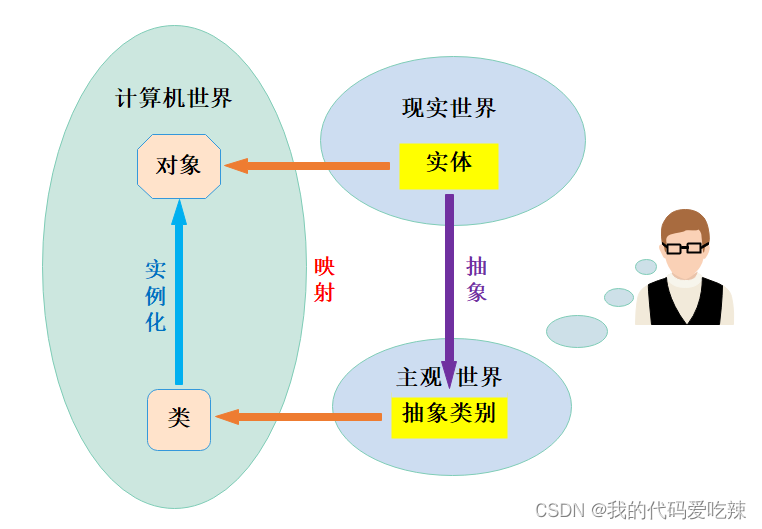
C++ 类与对象(下)
✅<1>主页:我的代码爱吃辣 📃<2>知识讲解:C 🔥<3>创作者:我的代码爱吃辣 ☂️<4>开发环境:Visual Studio 2022 💬<5>前言:C类与对象的收尾工作&#…...

Java基础——I/O
一、异常 异常是程序中可能出现的问题,它的父类是Exception。异常分为两类,编译时异常、运行时异常。 编译时异常:没有继承RuntimeException的异常,直接继承于Exception。编译阶段就会错误提示。运行时异常:RuntimeE…...
关于@hide的理解
在上一篇文章《学习HandlerThread》我们提到虽然HandlerThread类里有getThreadHandler()方法得到Handler,但是我们不可能调用到它。因为这个方法用hide注释了 /*** return a shared {link Handler} associated with this thread* hide*/NonNullpublic Handler getT…...

使用python加密主机文件几种方法实现
本文主要介绍了使用python加密主机文件几种方法实现,文中通过示例代码介绍的非常详细,对大家的学习或者工作具有一定的参考学习价值,需要的朋友们下面随着小编来一起学习学习吧数据加密是一种保护数据安全的技术,通过对数据进行编…...

西湖论剑 2023 比赛复现
WEB real_ez_node 在 route/index.js 中: router.post(/copy,(req,res)>{res.setHeader(Content-type,text/html;charsetutf-8)var ip req.connection.remoteAddress;console.log(ip);var obj {msg: ,}if (!ip.includes(127.0.0.1)) {obj.msg"only for…...

微信小程序更换管理员/重置管理员
方式1: 首先进入微信公众平台官网进入并登录后在管理中找到成员管理选项找到管理员点击后方的修改选项需要使用原管理员的微信进行扫码验证扫码后在手机上确认绑定新管理员,注意:如果是个人账号不可以更改成其他人。 方式2:原管…...
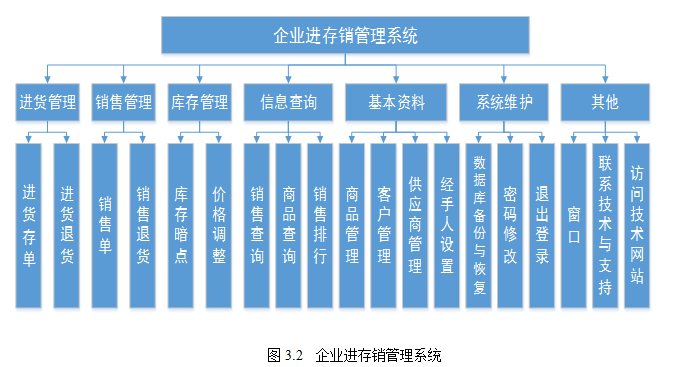
企业进存销管理系统
技术:Java、JSP等摘要:随着当今世界计算机技术的飞速发展,计算机在企业管理中应用的普及,利用计算机实现企业进销存管理势在必行。本系统结合公司实际的进销存制度,通过对本公司的供应商、客户、商品、进货、销售、进销…...
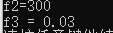
C++入门
变量变量创建的语法: 数据类型 变量名 变量初始值;int a 10;cout << a << endl;常量作用:用于记录程序中不可更改的教国C定义常量两种方式1).#define 宏常量:#define 常量名 常量值通常在文件上方定义。表示一个常量2).const 修饰的变量const 数据类型 常量名 常…...
- H264码流如何在SPS中获取宽高信息?)
视频知识点(20)- H264码流如何在SPS中获取宽高信息?
《音视频开发》系列-总览 前沿 了解H264视频编码格式的小伙伴都知道,H264编码中存在两个非常重要的参数集。没错,它们就是序列参数集(SPS)和图像参数集(PPS),而且通常情况下,PPS会依赖SPS中的部分参数信息,同时,视频码流的宽高信息也存储在SPS中。那么如何从中获取视…...
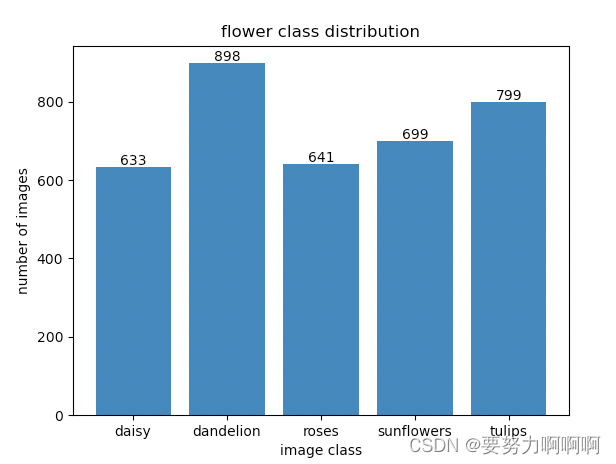
鲜花数据集实验结果总结
从read_split_data中得到:训练数据集,验证数据集,训练标签,验证标签。的所有的具体详细路径 数据集位置:https://download.csdn.net/download/guoguozgw/87437634 import os #一种轻量级的数据交换格式, …...
ElasticJob-Lite架构篇 - 认知分布式任务调度ElasticJob-Lite
前言 本文基于 ElasticJob-Lite 3.x 版本展开分析。 如果 Quartz 集群中有多个服务端节点,任务决定在哪个服务端节点上执行的呢? Quartz 采用随机负载,通过 DB 抢占下一个即将触发的 Trigger 绑定的任务的执行权限。 在 Quartz 的基础上&…...

超短脉冲激光自聚焦效应
前言与目录 强激光引起自聚焦效应机理 超短脉冲激光在脆性材料内部加工时引起的自聚焦效应,这是一种非线性光学现象,主要涉及光学克尔效应和材料的非线性光学特性。 自聚焦效应可以产生局部的强光场,对材料产生非线性响应,可能…...
)
Java 语言特性(面试系列1)
一、面向对象编程 1. 封装(Encapsulation) 定义:将数据(属性)和操作数据的方法绑定在一起,通过访问控制符(private、protected、public)隐藏内部实现细节。示例: public …...

【JavaEE】-- HTTP
1. HTTP是什么? HTTP(全称为"超文本传输协议")是一种应用非常广泛的应用层协议,HTTP是基于TCP协议的一种应用层协议。 应用层协议:是计算机网络协议栈中最高层的协议,它定义了运行在不同主机上…...

ETLCloud可能遇到的问题有哪些?常见坑位解析
数据集成平台ETLCloud,主要用于支持数据的抽取(Extract)、转换(Transform)和加载(Load)过程。提供了一个简洁直观的界面,以便用户可以在不同的数据源之间轻松地进行数据迁移和转换。…...

什么是EULA和DPA
文章目录 EULA(End User License Agreement)DPA(Data Protection Agreement)一、定义与背景二、核心内容三、法律效力与责任四、实际应用与意义 EULA(End User License Agreement) 定义: EULA即…...

均衡后的SNRSINR
本文主要摘自参考文献中的前两篇,相关文献中经常会出现MIMO检测后的SINR不过一直没有找到相关数学推到过程,其中文献[1]中给出了相关原理在此仅做记录。 1. 系统模型 复信道模型 n t n_t nt 根发送天线, n r n_r nr 根接收天线的 MIMO 系…...

用机器学习破解新能源领域的“弃风”难题
音乐发烧友深有体会,玩音乐的本质就是玩电网。火电声音偏暖,水电偏冷,风电偏空旷。至于太阳能发的电,则略显朦胧和单薄。 不知你是否有感觉,近两年家里的音响声音越来越冷,听起来越来越单薄? —…...

并发编程 - go版
1.并发编程基础概念 进程和线程 A. 进程是程序在操作系统中的一次执行过程,系统进行资源分配和调度的一个独立单位。B. 线程是进程的一个执行实体,是CPU调度和分派的基本单位,它是比进程更小的能独立运行的基本单位。C.一个进程可以创建和撤销多个线程;同一个进程中…...

[ACTF2020 新生赛]Include 1(php://filter伪协议)
题目 做法 启动靶机,点进去 点进去 查看URL,有 ?fileflag.php说明存在文件包含,原理是php://filter 协议 当它与包含函数结合时,php://filter流会被当作php文件执行。 用php://filter加编码,能让PHP把文件内容…...

【从零开始学习JVM | 第四篇】类加载器和双亲委派机制(高频面试题)
前言: 双亲委派机制对于面试这块来说非常重要,在实际开发中也是经常遇见需要打破双亲委派的需求,今天我们一起来探索一下什么是双亲委派机制,在此之前我们先介绍一下类的加载器。 目录 编辑 前言: 类加载器 1. …...
