el-select 多选，选有一个未选择的选项
多选有未选择这个选项后。会出现一个情况，绑定的数据为[‘未选择’,‘cpu1’,‘cpu2’]
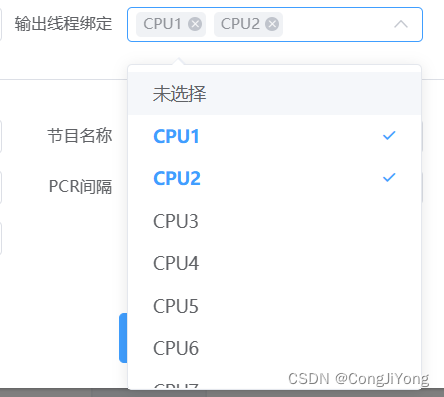
进行一个处理，选择（未选择）就清除（其它的选择），选择（cpu）就清除（未选择的选中）
处理后不会出现未选择和cpu同时选中的情况
<el-select v-model='this.Form1.cpuBind' @change='CpuChange("cpuBind")'><el-option value='close' label='未选择'></el-option>//cpu...
</el-select>
//el-selcet绑定change事件 调用CpuChange('el-select绑定的变量名')
//close是未选择的option的value
CpuChange(value){if (this.Form1[value].length > 1 && this.Form1[value].includes('close')) {let index = this.Form1[value].indexOf('close')let isLastElement = index === this.Form1[value].length - 1if (isLastElement) {this.Form1[value]= ['close']} else {if (index !== -1) {this.Form1[value].splice(index, 1)}}}},
相关文章：
el-select 多选，选有一个未选择的选项
多选有未选择这个选项后。会出现一个情况，绑定的数据为[‘未选择’,‘cpu1’,‘cpu2’] 进行一个处理，选择（未选择）就清除（其它的选择），选择（cpu）就清除（未选…...
CISSP 第6章： 密码学与对称加密算法
第六章 密码学与对称加密算法 6.1 密码学历史上的里程碑 6.1.1 凯撒密码 简单的将字母表中的每个字母替换成其后的三个字母，是单一字母的替代置换密码 6.1.2 美国内战 美国内战使用词汇替代和置换的复杂组合，从而试图破坏敌人的破译企图 6.1.3 Ultra与…...
《深入理解C++11：C++11新特性解析与应用》笔记八
第八章 融入实际应用 8.1 对齐支持 8.1.1 数据对齐 c可以通过sizeof查询数据的长度，但是没有对对齐方式有关的查询或者设定进行标准化。c11标准定义的alignof函数可以查看数据的对齐方式。 现在的计算机通常会支持许多向量指令，4组8字节的浮点数据&a…...
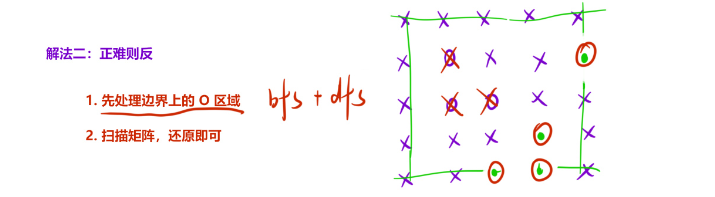
算法——BFS解决FloodFill算法
什么是FloodFill算法 中文：洪水灌溉。假设这一块4*4的方格是一块土地，有凸起的地方，也有凹陷的地方（凹陷的地方用负数表示）。此时下大雨发洪水，会把凹陷的地方填满。绿色圈起来的属于一块区域（…...
【Linux】常用的基本命令指令②
前言：前面我们学习了Linux的部分指令，今天我们将接着上次的部分继续将Linux剩余的基本指令. 💖 博主CSDN主页:卫卫卫的个人主页 💞 👉 专栏分类:Linux的学习 👈 💯代码仓库:卫卫周大胖的学习日记…...
52、全连接 - 特征与样本空间的对应关系
上一节说到经过全连接层之后，神经网络学习到的特征，会从隐层特征空间逐步映射到样本空间，这主要是由于全连接层可以融合全局的特征。 在经过全连接层之后，在 ResNet50 这个神经网络中会输出1000个特征的得分值，这1000个特征的得分值，便可以对应到图像的分类。 怎么对应…...
Go语言中的包管理工具之Go Vendor的使用
GoLang 中常用的包管理的方式 常用的有三种 Go PathGo VendorGo Modules 关于 Go Vender 1 ）概述 在2015年的时候，我们的另一个包管理工具Go Vendor就诞生了它诞生于 2015.8.19 ，是在Go的 1.5 版本当中引入的，它默认是关闭的我…...
QString设置小数点精度位数
QString设置小数点精度位数 Chapter1 QString设置小数点精度位数Chapter2 Qt中QString.toDouble有效位数6位问题以及数据小数点有效位数的处理问题一：QString.toDouble有效位只有6位问题二:小数点有效位数的问题 Chapter3 qt QString转Double只显示6位数字的问题(精…...
基于Java驾校预约管理系统
基于Java的驾校预约管理系统是一个为驾校提供在线预约服务的系统。该系统利用Java编程语言，采用SSM框架，并使用MySQL数据库进行开发。 这个系统主要有三个角色：用户、教练和管理员。 用户可以注册和登录系统，查看驾校的公告信息…...
C++面向对象高级编程（侯捷）笔记2
侯捷C面向对象高级编程 本文是学习笔记，仅供个人学习使用，如有侵权，请联系删除。 如果你对C面向对象的组合、继承和委托不了解，对什么是拷贝构造、什么是拷贝赋值和析构不清楚，对类设计中的Adapter、pImpl、Template…...
 优化麦克劳林公式)
双曲正弦函数(*) 优化麦克劳林公式
#include<stdio.h> #include<math.h> int main() {double x,eps,i3,y,item;scanf("%lf%lf",&x,&eps);yx;itemx;while(fabs(item)>eps){itemitem*x*x/i/(i-1);i2;yitem;}printf("%.6f\n",y);return 0; }...
无监督关键词提取算法:TF-IDF、TextRank、RAKE、YAKE、 keyBERT
TF-IDF TF-IDF是一种经典的基于统计的方法，TF(Term frequency)是指一个单词在一个文档中出现的次数，通常一个单词在一个文档中出现的次数越多说明该词越重要。IDF(Inverse document frequency)是所有文档数比上出现某单词的个数，通常一个单词…...
web3 : blockscout剖析
Blockscout 是第一个功能齐全的开源区块链浏览器，可供任何以太坊虚拟机 (EVM) 链使用。项目方可以下载并使用Blockscout作为其链的浏览器，用户可以轻松验证交易、余额、区块确认、智能合约和其他记录。 目录 Blockscout可以做什么主要特征blockscoutDocker容器组件Postgres 1…...
【机器学习基础】DBSCAN
🚀个人主页：为梦而生~ 关注我一起学习吧！ 💡专栏：机器学习 欢迎订阅！相对完整的机器学习基础教学！ ⭐特别提醒：针对机器学习，特别开始专栏：机器学习python实战…...
计算机硬件 4.4键盘与鼠标
第四节 键盘与鼠标 一、认识键盘 1.地位：计算机系统最基本的输入设备。 2.外观结构：面板、键帽、底盘、数据线。 3.组成键区：主键区、功能键区、辅助键区和编辑（控制）键区。 二、键盘分类 1.按接口分 ①AT口&…...
Flappy Bird QDN PyTorch博客 - 代码解读
Flappy Bird QDN PyTorch博客 - 代码解读 介绍环境配置项目目录结构QDN算法重要函数解读preprocess(observation)DeepNetWork(nn.Module)BirdDQN类主程序部分 介绍 在本博客中，我们将介绍如何使用QDN（Quantile Dueling Network）算法…...
听GPT 讲Rust源代码--compiler(9)
File: rust/compiler/rustc_trait_selection/src/traits/select/mod.rs 在Rust源代码中，rust/compiler/rustc_trait_selection/src/traits/select/mod.rs文件的作用是实现Rust编译器的trait选择器。 首先，让我们逐个介绍这些struct的作用： Se…...
Go语言中关于go get, go install, go build, go run指令
go get go get 它会执行两个操作 第一个, 是先将远程的代码克隆到Go Path的 src 目录那二个, 是执行go install命令 那如果指定的包可以生成二进制文件那它就会把这个二进制文件保存到这个 Go Path 的bin目录下面这是 go install 命令执行的操作 如果只需要下载包，…...
石头剪刀布游戏 - 华为OD统一考试
OD统一考试 分值： 100分 题解： Java / Python / C++ 题目描述 石头剪刀布游戏有 3 种出拳形状: 石头、剪刀、布。分别用字母 A,B,C 表示游戏规则： 出拳形状之间的胜负规则如下: A>B; B>C; C>A； 左边一个字母，表示相对优势形状。右边一个字母，表示相对劣势形状。…...
【北亚服务器数据恢复】ZFS文件系统服务器ZPOOL下线的数据恢复案例
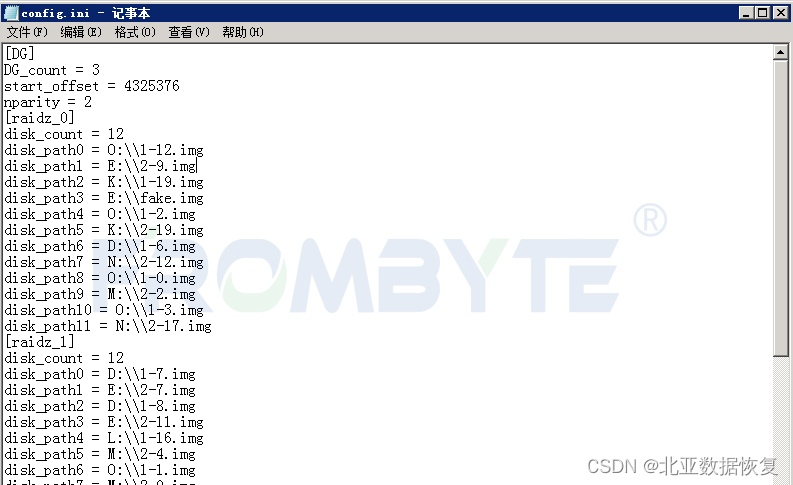
服务器数据恢复环境： 服务器中有32块硬盘，组建了3组RAIDZ，部分磁盘作为热备盘。zfs文件系统。 服务器故障： 服务器运行中突然崩溃，排除断电、进水、异常操作等外部因素。工作人员将服务器重启后发现无法进入操作系统。…...
RestClient
什么是RestClient RestClient 是 Elasticsearch 官方提供的 Java 低级 REST 客户端，它允许HTTP与Elasticsearch 集群通信，而无需处理 JSON 序列化/反序列化等底层细节。它是 Elasticsearch Java API 客户端的基础。 RestClient 主要特点 轻量级ÿ…...
Leetcode 3576. Transform Array to All Equal Elements
Leetcode 3576. Transform Array to All Equal Elements 1. 解题思路2. 代码实现 题目链接：3576. Transform Array to All Equal Elements 1. 解题思路 这一题思路上就是分别考察一下是否能将其转化为全1或者全-1数组即可。 至于每一种情况是否可以达到…...
基于ASP.NET+ SQL Server实现（Web）医院信息管理系统
医院信息管理系统 1. 课程设计内容 在 visual studio 2017 平台上，开发一个“医院信息管理系统”Web 程序。 2. 课程设计目的 综合运用 c#.net 知识，在 vs 2017 平台上，进行 ASP.NET 应用程序和简易网站的开发；初步熟悉开发一…...
FastAPI 教程：从入门到实践
FastAPI 是一个现代、快速（高性能）的 Web 框架，用于构建 API，支持 Python 3.6。它基于标准 Python 类型提示，易于学习且功能强大。以下是一个完整的 FastAPI 入门教程，涵盖从环境搭建到创建并运行一个简单的…...
基于服务器使用 apt 安装、配置 Nginx
🧾 一、查看可安装的 Nginx 版本 首先，你可以运行以下命令查看可用版本： apt-cache madison nginx-core输出示例： nginx-core | 1.18.0-6ubuntu14.6 | http://archive.ubuntu.com/ubuntu focal-updates/main amd64 Packages ng…...
【git】把本地更改提交远程新分支feature_g
创建并切换新分支 git checkout -b feature_g 添加并提交更改 git add . git commit -m “实现图片上传功能” 推送到远程 git push -u origin feature_g...
【JavaSE】绘图与事件入门学习笔记
-Java绘图坐标体系 坐标体系-介绍 坐标原点位于左上角，以像素为单位。 在Java坐标系中,第一个是x坐标,表示当前位置为水平方向，距离坐标原点x个像素;第二个是y坐标，表示当前位置为垂直方向，距离坐标原点y个像素。 坐标体系-像素 …...
初学 pytest 记录
安装 pip install pytest用例可以是函数也可以是类中的方法 def test_func():print()class TestAdd: # def __init__(self): 在 pytest 中不可以使用__init__方法 # self.cc 12345 pytest.mark.api def test_str(self):res add(1, 2)assert res 12def test_int(self):r…...
USB Over IP专用硬件的5个特点
USB over IP技术通过将USB协议数据封装在标准TCP/IP网络数据包中，从根本上改变了USB连接。这允许客户端通过局域网或广域网远程访问和控制物理连接到服务器的USB设备（如专用硬件设备），从而消除了直接物理连接的需要。USB over IP的…...
【从零开始学习JVM | 第四篇】类加载器和双亲委派机制(高频面试题)
前言： 双亲委派机制对于面试这块来说非常重要，在实际开发中也是经常遇见需要打破双亲委派的需求，今天我们一起来探索一下什么是双亲委派机制，在此之前我们先介绍一下类的加载器。 目录 编辑 前言： 类加载器 1. …...