自动化测试怎么做?看完你就懂了。。。
前言
我想应该有很多测试人员应该有这样的疑虑,自动化测试要怎么去做,现在我把自己的一些学习经验分享给大家,希望对你们有帮助,有说的不好的地方,还请多多指教!
对于测试人员来说,不管进行功能测试还是自动化测试还是性能测试都是需要编写测试用例,所以我们必须先要了解清楚手工测试用例与自动化测试用例的一些特点,才能更好的开展自动化测试工作。

自动化测试用例设计
手工测试用例和自动化测试用例
手工测试用例是针对功能测试人员的,而自动化测试用例是针对自动化测试用例框架或工具的。
(1)手工测试用例特点
较好的异常处理能力,能通过人为的逻辑判断校验当前步骤是否正确实现;
人工执行用例具有一定步骤跳跃性;
人工测试步步跟踪,能够细致定位问题;
主要用来发现功能缺陷;
(2)自动化测试用例特点
执行对象是脚本,任何一个盘算都需要编码定义;
用例步骤之间关联性强;
主要用来保证产品主体功能正确和完整,让测试人员从繁琐重复的工作中解脱出来;
目前自动化测试阶段定位在冒烟测试和回归测试
注意:通过对比发现,自动化测试不能完全替代手工测试,自动化测试的目的仅仅在于让测试人员从繁琐重复的测试流程中解脱出来,把更多的时间和精力放在更有价值的测试中,例如探索性测试。
(3)自动化测试用例注意事项
1、不是所有手工测试用例都要转为自动化测试用例
2、考虑到脚本开发成本,不要选择流程太复杂的用例,如果有必要,可以考虑把流程拆分成多个用例来实现脚本
3、选择的用例最好可以构建场景。例如,一个功能模块,分成多个用例,多个用例使用同一个场景,这样的好处在于方便构建关键字测试模型。
4、选择用例可以带有目的性。例如,这部分用例作冒烟测试等,当然,会存在重叠关系,如果当前用例不满足需求,那么唯有修改用例来适应脚本和需求
5、选取的用例可以是主体流程,这部分用于冒烟测试(https://baike.so.com/doc/6504729-6718449.html,如果不了解专业术语,下来要花费功夫哦)
6、选取的测试用例可以是你认为重复执行,很猥琐的部分。例如字段验证、提示信息验证之类,这部分适用于回归测试
7、自动化测试也可以用来做配置检查、数据库检查。这些可能超过了手工用例,但也算用例拓展的一部分,项目负责人可以有选择的增加
8、平时在手工测试时,如果需要构造一些复杂的数据或重复一些简单的机械式动作,则告诉脚本,让它来帮你,或许你的效率会因此提高。
在这我为大家准备了一份软件测试视频教程(含面试、接口、自动化、性能测试等),就在下方,需要的可以直接去观看,也可以直接【点击文末小卡片免费领取资料文档】
软件测试视频教程观看处:
【2024最新版】Python自动化测试15天从入门到精通,10个项目实战,允许白嫖。。。
自动化测试类型
1、测试静态内容
静态内容测试是最简单的测试,用于验证静态的、不变的ui元素的存在性,例如:
(1)每个页面都有预期的页面标题,这可以用来验证链接指向一个预期页面
(2)应用程序的主页包含一个应该在页面顶部的图片
(3)网站的每个页面是否包含一个页脚区域来显示公司的联系方式、隐私政策以及商标信息等
(4)每一页的标题文本都使用<h1>标签吗?每个页面是否都有正确的头部文本
你可能需要(也可能不需要)对页面内容进行自动化测试。如果你的网页是不易受到影响的,则手工对内容进行测试就足够了。假设你的应用文件的位置移动了,则内容测是就非常有价值
2、测试链接
web站点的一个常见错误为失效的链接或链接指向无效页。链接测试涉及各个链接和验证预期的页面是否存在。如果静态链接不经常更改,则手动测试就足够了。但是,如果你的网页设计师经常修改链接或者文件不时被重定向,则链接测试应该实现自动化。
3、功能测试
在你的应用程序中,需要测试应用的特定功能,需要一些类型的用户输入,并返回某种类型的结果,通常一个功能测试涉及多个页面,一个基于表单的输入页面,其中包含若干输入字段,提交和取消操作,以及一个或多个响应页面。用户输入可以通过文本输入域、复选框、下拉列表,或任何其他浏览器所支持输入。
功能测试通常是需要自动化测试的 最复杂的测试类型,但通常也是最重要的。典型的测试是登陆,注册网站账户用户账户操作、账户设置变化、复杂的数据检索操作等等。功能测试通常对应着你的应用程序的描述应用特性或设计的使用场景。
4、测试动态元素
通常网页元素都有唯一的标识符,用于唯一的定位该网页的元素。通常情况下,唯一标识符用html标记的id属性或name属性来实现。
5、Ajax的测试
Ajax是一种支持以及动态改变用户界面元素的技术。页面元素可以动态更改,但不需要浏览器重新载入页面,如动画,RSS源、其他实时数据更新等。
Ajax有无数更新网页上元素的放大,最简单的方式是在Ajax驱动的应用程序中,数据可以从应用服务器检索,然后显示在页面上,而不需要重新加载整个页面,只有一小部分的页面,或者只有元素本身重新被加载。
最后跟大家分享一下自动化测试用例编写原则:
自动化测试用例编写原则
1.一个用例为一个完整的场景,从用户登录系统到 最终退出并关闭浏览器
2.一个用例只验证一个功能点,不要试图在用户登录系统后把所有功能都验证一遍
3.尽可能少的编写逆向逻辑用例。一方面因为逆向逻辑的用力很多(例如,手机号输错有几十种情况),另一个方面自动化脚本本身比较脆弱,复杂的逆向逻辑用例实现起来比较麻烦且容易出错。
4.用例与用例之间尽量避免产生依赖
5.一条用例完成测试之后需要对测试场景进行还原,以免影响其他用例的执行
结语
最后感谢每一个认真阅读我文章的人,礼尚往来总是要有的,虽然不是什么很值钱的东西,如果你用得到的话可以直接拿走:
这些资料,对于做【软件测试】的朋友来说应该是最全面最完整的备战仓库,这个仓库也陪伴我走过了最艰难的路程,希望也能帮助到你!凡事要趁早,特别是技术行业,一定要提升技术功底。
相关文章:

自动化测试怎么做?看完你就懂了。。。
前言 我想应该有很多测试人员应该有这样的疑虑,自动化测试要怎么去做,现在我把自己的一些学习经验分享给大家,希望对你们有帮助,有说的不好的地方,还请多多指教! 对于测试人员来说,不管进行功…...

小秋SLAM入门实战opencv所有文章汇总
opencv_core和 opencv_imgcodecs是 OpenCV(开源计算机视觉库)的两个主要模块 【如何使用cv::erode()函数对图像进行腐蚀操作】 头文件用途 用OpenCV创建一张类型为CV_8UC1的单通道随机灰度图像 用OpenCV创建一张灰度黑色图像并设置某一列为白色 OpenCV创…...

2023年终总结(脚踏实地,仰望星空)
回忆录 2023年,经历非常多的大事情,找工作、实习、研究生毕业、堂哥结婚、大姐买车、申博、读博、参加马拉松,有幸这一年全家人平平安安,在稳步前进。算是折腾的一年,杭州、赣州、武汉、澳门、珠海、遵义来回跑。完成…...

Transforer逐模块讲解
本文将按照transformer的结构图依次对各个模块进行讲解: 可以看一下模型的大致结构:主要有encode和decode两大部分组成,数据经过词embedding以及位置embedding得到encode的时输入数据 输入部分 embedding就是从原始数据中提取出单词或位置&…...

macOS进程间通信的常用技术汇总
macOS进程间通信的常用技术汇总 命令行传参。yyds管道(pipe), 匿名管道, c的技术,可以跨平台使用 只能在父子进程间通信,由于是单向的管道,只能单方面传输数据。 如果需要双向传输,需要建立双向的两条管道才行 匿名管…...

高德地图信息窗体设置
1. 添加默认信息窗体 //构建信息窗体中显示的内容var info [];info.push(<div style"height: 36px; line-height: 45px; padding: 0px 20px; white-space:nowrap;">位置:北京</div>);info.push(<div style"height: 36px; line-heig…...
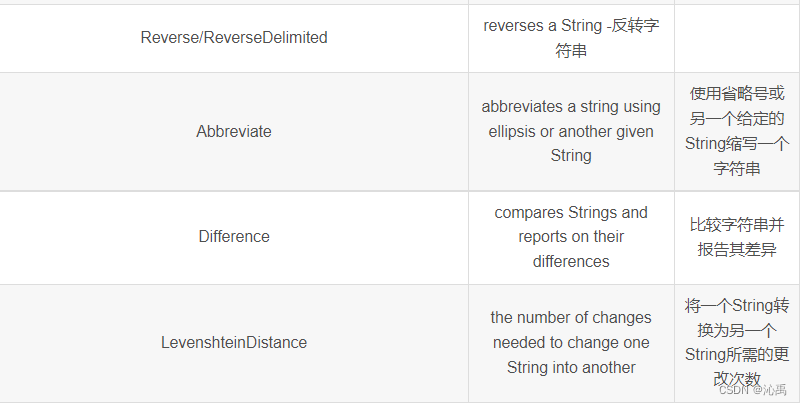
isEmpty 和 isBlank 的用法区别,居然一半的人答不上来.....
isEmpty 和 isBlank 的用法区别 isEmpty系列isBank系列 hi!我是沁禹~ 也许你两个都不知道,也许你除了isEmpty/isNotEmpty/isNotBlank/isBlank外,并不知道还有isAnyEmpty/isNoneEmpty/isAnyBlank/isNoneBlank的存在, come on ,让我们一起来探索org.apache…...

数据分析求职-简历准备
简历在整个求职过程中的重要性不言而喻,今天咱们来聊求职过程中简历准备的那些事儿~ 1. 简历究竟有啥用 求职的流程简单说就是:网申->笔试->面试->offer 其中网申环节,简历100%决定了你的通过与否,这个点大家都知道。…...
亚马逊店铺遇到账号申诉模版分享
1.表达诚意,先认错再说:我知道,最近我们在Amazon.com上作为卖家的表现已经低于亚马逊和我们自己的质量标准。 2.清楚分明的格式:我们库存管理的混乱导致了延迟发货,更糟糕的是,物品无法使用。当延迟发货和…...

2023年广东省网络安全A模块(笔记详解)
模块A 基础设施设置与安全加固 一、项目和任务描述: 假定你是某企业的网络安全工程师,对于企业的服务器系统,根据任务要求确保各服务正常运行,并通过综合运用登录和密码策略、流量完整性保护策略、事件监控策略、防火墙策略等多…...
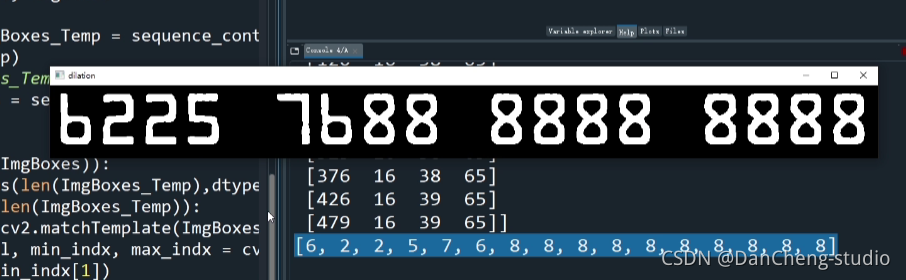
竞赛保研 基于机器视觉的银行卡识别系统 - opencv python
1 前言 🔥 优质竞赛项目系列,今天要分享的是 基于深度学习的银行卡识别算法设计 该项目较为新颖,适合作为竞赛课题方向,学长非常推荐! 🧿 更多资料, 项目分享: https://gitee.com/dancheng…...

书摘:C 嵌入式系统设计模式 04
本书的原著为:《Design Patterns for Embedded Systems in C ——An Embedded Software Engineering Toolkit 》,讲解的是嵌入式系统设计模式,是一本不可多得的好书。 本系列描述我对书中内容的理解。 实现类的最简单方法是使用文件作为封装…...

C 练习实例16 - 最大公约数和最小公倍数
题目:输入两个正整数a和b,求其最大公约数和最小公倍数 数学:最大公约数*最小公倍数a*b 例如:a16,b20。最小公倍数80,最大公约数4。80*416*20。 算法:辗转相除法,又称欧几里德算法…...

GAN-概念和应用场景
概念和应用 生成对抗网络 (GAN) 的 18 个令人印象深刻的应用 by 杰森布朗利 on July 12, 2019 in 生成对抗网络110 鸣叫 共享 生成对抗网络 (GAN) 是一种用于生成建模的神经网络架构。 生成式建模涉及使用模型生成可…...

LeetCode(36)有效的数独 ⭐⭐
请你判断一个 9 x 9 的数独是否有效。只需要 根据以下规则 ,验证已经填入的数字是否有效即可。 数字 1-9 在每一行只能出现一次。数字 1-9 在每一列只能出现一次。数字 1-9 在每一个以粗实线分隔的 3x3 宫内只能出现一次。(请参考示例图) 注…...

用LCD显示字符‘A‘
#include<reg51.h> //包含单片机寄存器的头文件 #include<intrins.h> //包含_nop_()函数定义的头文件 sbit RSP2^0; //寄存器选择位,将RS位定义为P2.0引脚 sbit RWP2^1; //读写选择位,将RW位定义为P2.1引脚 sbit EP2^2; //使能…...
)
Zookeeper相关问题及答案(2024)
1、ZooKeeper是什么?它的主要用途是什么? ZooKeeper 是一个由 Apache 预先开发和维护的开源服务器,用于协调分布式应用程序。它是一个集中式服务,为分布式应用提供一致性保障,配置管理,命名,同…...

1.大数据概述
目录 概述hadoophadoop 模块hadoop 发行版apache社区版本CDP(CDHHDP)其它云产商框架选择 hadoop 安装 结束 概述 先了解几个常用的网站 apache 官网hadoop 官网hadoop githubhttps://github.com/apache/xxx [https://github.com/apache/spark (example)] hadoop hadoop 模块…...

NGUI基础-Widget
目录 Widget是什么 Widget组件包含的属性 Pivot Depth Size snap Aspect Free Based on Width Based on Height Widget是什么 在Unity UI系统中,"Widget"是指UI元素的基类,它为UI元素提供了位置、大小和锚点等基本属性。通过使用&qu…...

SpringBoot集成沙箱支付
前言 支付宝沙箱支付(Alipay Sandbox Payment)是支付宝提供的一个模拟支付环境,用于开发和测试支付宝支付功能的开发者工具。在真实的支付宝环境中进行支付开发和测试可能涉及真实资金和真实用户账户,而沙箱环境则提供了一个安全…...

Golang 面试经典题:map 的 key 可以是什么类型?哪些不可以?
Golang 面试经典题:map 的 key 可以是什么类型?哪些不可以? 在 Golang 的面试中,map 类型的使用是一个常见的考点,其中对 key 类型的合法性 是一道常被提及的基础却很容易被忽视的问题。本文将带你深入理解 Golang 中…...

学习STC51单片机31(芯片为STC89C52RCRC)OLED显示屏1
每日一言 生活的美好,总是藏在那些你咬牙坚持的日子里。 硬件:OLED 以后要用到OLED的时候找到这个文件 OLED的设备地址 SSD1306"SSD" 是品牌缩写,"1306" 是产品编号。 驱动 OLED 屏幕的 IIC 总线数据传输格式 示意图 …...

令牌桶 滑动窗口->限流 分布式信号量->限并发的原理 lua脚本分析介绍
文章目录 前言限流限制并发的实际理解限流令牌桶代码实现结果分析令牌桶lua的模拟实现原理总结: 滑动窗口代码实现结果分析lua脚本原理解析 限并发分布式信号量代码实现结果分析lua脚本实现原理 双注解去实现限流 并发结果分析: 实际业务去理解体会统一注…...

在WSL2的Ubuntu镜像中安装Docker
Docker官网链接: https://docs.docker.com/engine/install/ubuntu/ 1、运行以下命令卸载所有冲突的软件包: for pkg in docker.io docker-doc docker-compose docker-compose-v2 podman-docker containerd runc; do sudo apt-get remove $pkg; done2、设置Docker…...

Rapidio门铃消息FIFO溢出机制
关于RapidIO门铃消息FIFO的溢出机制及其与中断抖动的关系,以下是深入解析: 门铃FIFO溢出的本质 在RapidIO系统中,门铃消息FIFO是硬件控制器内部的缓冲区,用于临时存储接收到的门铃消息(Doorbell Message)。…...

初学 pytest 记录
安装 pip install pytest用例可以是函数也可以是类中的方法 def test_func():print()class TestAdd: # def __init__(self): 在 pytest 中不可以使用__init__方法 # self.cc 12345 pytest.mark.api def test_str(self):res add(1, 2)assert res 12def test_int(self):r…...

基于 TAPD 进行项目管理
起因 自己写了个小工具,仓库用的Github。之前在用markdown进行需求管理,现在随着功能的增加,感觉有点难以管理了,所以用TAPD这个工具进行需求、Bug管理。 操作流程 注册 TAPD,需要提供一个企业名新建一个项目&#…...

C# 表达式和运算符(求值顺序)
求值顺序 表达式可以由许多嵌套的子表达式构成。子表达式的求值顺序可以使表达式的最终值发生 变化。 例如,已知表达式3*52,依照子表达式的求值顺序,有两种可能的结果,如图9-3所示。 如果乘法先执行,结果是17。如果5…...
 error)
【前端异常】JavaScript错误处理:分析 Uncaught (in promise) error
在前端开发中,JavaScript 异常是不可避免的。随着现代前端应用越来越多地使用异步操作(如 Promise、async/await 等),开发者常常会遇到 Uncaught (in promise) error 错误。这个错误是由于未正确处理 Promise 的拒绝(r…...

自然语言处理——文本分类
文本分类 传统机器学习方法文本表示向量空间模型 特征选择文档频率互信息信息增益(IG) 分类器设计贝叶斯理论:线性判别函数 文本分类性能评估P-R曲线ROC曲线 将文本文档或句子分类为预定义的类或类别, 有单标签多类别文本分类和多…...
