复试 || 就业day04(2024.01.05)项目一
文章目录
- 前言
- 线性回归房价预测
- 加载数据
- 数据查看
- 数据拆分
- 数据建模
- 模型的验证、应用
- 模型的评估
- 总结
前言
💫你好,我是辰chen,本文旨在准备考研复试或就业
💫本文内容来自某机构网课,是我为复试准备的第一个项目
💫欢迎大家的关注,我的博客主要关注于考研408以及AIoT的内容
🌟 预置知识详见我的AIoT板块,需掌握 基本Python语法, Numpy, Pandas, Matplotlib
以下的几个专栏是本人比较满意的专栏(大部分专栏仍在持续更新),欢迎大家的关注:
💥ACM-ICPC算法汇总【基础篇】
💥ACM-ICPC算法汇总【提高篇】
💥AIoT(人工智能+物联网)
💥考研
💥CSP认证考试历年题解
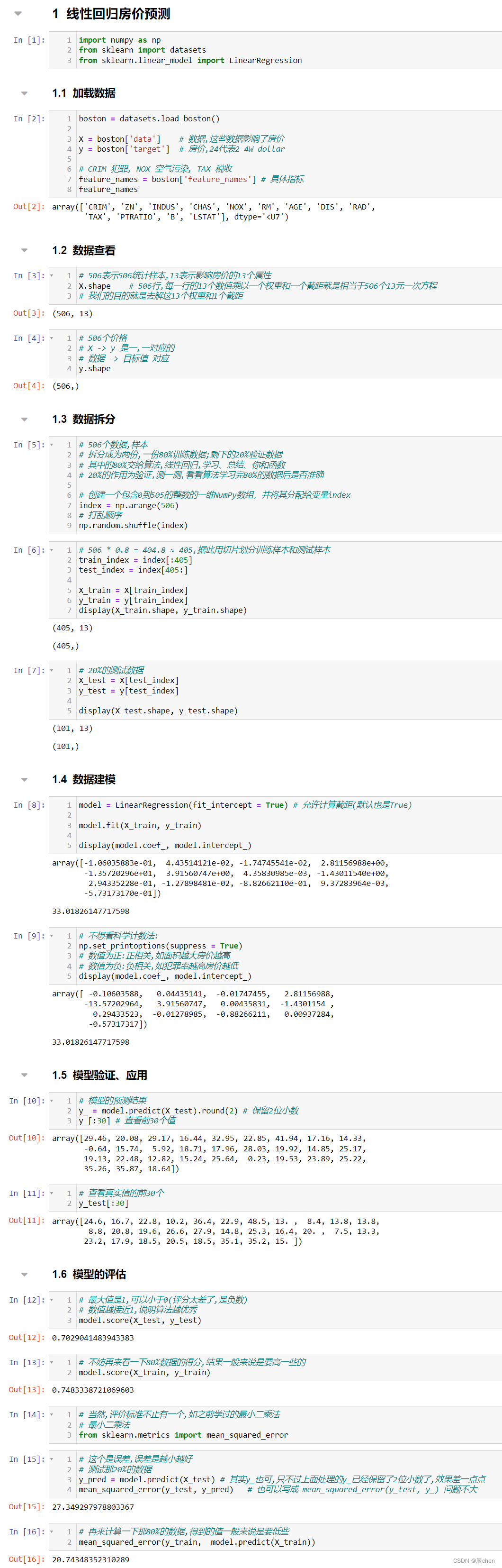
线性回归房价预测
import numpy as np
from sklearn import datasets
from sklearn.linear_model import LinearRegression
加载数据
boston = datasets.load_boston()X = boston['data'] # 数据,这些数据影响了房价
y = boston['target'] # 房价,24代表2 4W dollar # CRIM 犯罪, NOX 空气污染, TAX 税收
feature_names = boston['feature_names'] # 具体指标
feature_names

数据查看
# 506表示506统计样本,13表示影响房价的13个属性
X.shape # 506行,每一行的13个数值乘以一个权重和一个截距就是相当于506个13元一次方程
# 我们的目的就是去解这13个权重和1个截距
# 506个价格
# X -> y 是一,一对应的
# 数据 -> 目标值 对应
y.shape
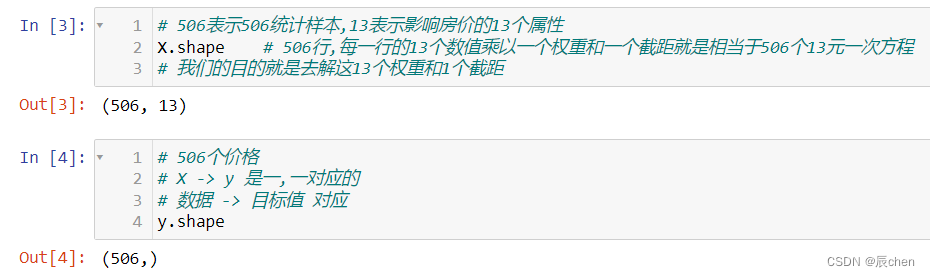
数据拆分
# 506个数据,样本
# 拆分成为两份,一份80%训练数据;剩下的20%验证数据
# 其中的80%交给算法,线性回归,学习、总结、你和函数
# 20%的作用为验证,测一测,看看算法学习完80%的数据后是否准确# 创建一个包含0到505的整数的一维NumPy数组,并将其分配给变量index
index = np.arange(506)
# 打乱顺序
np.random.shuffle(index)
# 506 * 0.8 = 404.8 ≈ 405,据此用切片划分训练样本和测试样本
train_index = index[:405]
test_index = index[405:]X_train = X[train_index]
y_train = y[train_index]
display(X_train.shape, y_train.shape)
# 20%的测试数据
X_test = X[test_index]
y_test = y[test_index]display(X_test.shape, y_test.shape)

数据建模
model = LinearRegression(fit_intercept = True) # 允许计算截距(默认也是True)model.fit(X_train, y_train)display(model.coef_, model.intercept_)
# 不想看科学计数法:
np.set_printoptions(suppress = True)
# 数值为正:正相关,如面积越大房价越高
# 数值为负:负相关,如犯罪率越高房价越低
display(model.coef_, model.intercept_)

模型的验证、应用
# 模型的预测结果
y_ = model.predict(X_test).round(2) # 保留2位小数
y_[:30] # 查看前30个值
# 查看真实值的前30个
y_test[:30]

模型的评估
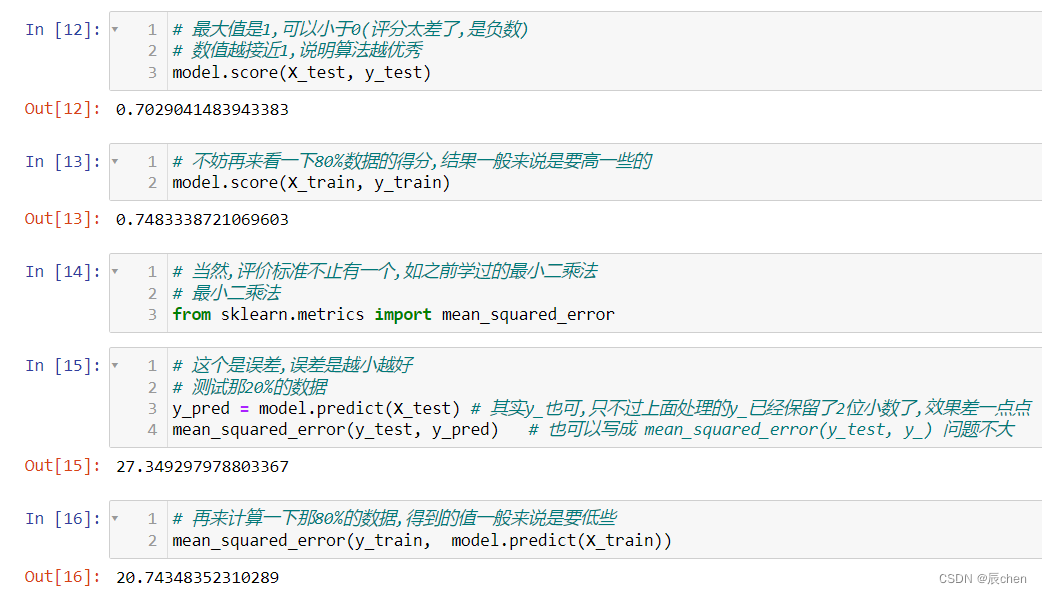
# 最大值是1,可以小于0(评分太差了,是负数)
# 数值越接近1,说明算法越优秀
model.score(X_test, y_test)
# 不妨再来看一下80%数据的得分,结果一般来说是要高一些的
model.score(X_train, y_train)
# 当然,评价标准不止有一个,如之前学过的最小二乘法
# 最小二乘法
from sklearn.metrics import mean_squared_error
# 这个是误差,误差是越小越好
# 测试那20%的数据
y_pred = model.predict(X_test) # 其实y_也可,只不过上面处理的y_已经保留了2位小数了,效果差一点点
mean_squared_error(y_test, y_pred) # 也可以写成 mean_squared_error(y_test, y_) 问题不大
# 再来计算一下那80%的数据,得到的值一般来说是要低些
mean_squared_error(y_train, model.predict(X_train))
总结
完整代码:
import numpy as np
from sklearn import datasets
from sklearn.linear_model import LinearRegression boston = datasets.load_boston()X = boston['data'] # 数据,这些数据影响了房价
y = boston['target'] # 房价,24代表2 4W dollar
# X.shape : (506, 13), y.shape : (506, )# CRIM 犯罪, NOX 空气污染, TAX 税收
feature_names = boston['feature_names'] # 具体指标# 创建一个包含0到505的整数的一维NumPy数组,并将其分配给变量index
index = np.arange(506)
# 打乱顺序
np.random.shuffle(index)# 506个数据,样本
# 拆分成为两份,一份80%训练数据;剩下的20%验证数据
# 其中的80%交给算法,线性回归,学习、总结、你和函数
# 20%的作用为验证,测一测,看看算法学习完80%的数据后是否准确
# 506 * 0.8 = 404.8 ≈ 405,据此用切片划分训练样本和测试样本
train_index = index[:405]
X_train = X[train_index]
y_train = y[train_index]# 20%的测试数据
test_index = index[405:]
X_test = X[test_index]
y_test = y[test_index]# 不想看科学计数法:
np.set_printoptions(suppress = True)
model = LinearRegression(fit_intercept = True) # 允许计算截距(默认也是True)
# 数值为正:正相关,如面积越大房价越高
# 数值为负:负相关,如犯罪率越高房价越低
model.fit(X_train, y_train)# 模型的预测结果
y_ = model.predict(X_test).round(2) # 保留2位小数
# 最大值是1,可以小于0(评分太差了,是负数)
# 数值越接近1,说明算法越优秀
model.score(X_test, y_test)# 不妨再来看一下80%数据的得分,结果一般来说是要高一些的
model.score(X_train, y_train)# 当然,评价标准不止有一个,如之前学过的最小二乘法
# 最小二乘法
from sklearn.metrics import mean_squared_error
# 这个是误差,误差是越小越好
# 测试那20%的数据
y_pred = model.predict(X_test) # 其实y_也可,只不过上面处理的y_已经保留了2位小数了,效果差一点点
mean_squared_error(y_test, y_pred) # 也可以写成 mean_squared_error(y_test, y_) 问题不大
# 再来计算一下那80%的数据,得到的值一般来说是要低些
mean_squared_error(y_train, model.predict(X_train))
相关文章:

复试 || 就业day04(2024.01.05)项目一
文章目录 前言线性回归房价预测加载数据数据查看数据拆分数据建模模型的验证、应用模型的评估 总结 前言 💫你好,我是辰chen,本文旨在准备考研复试或就业 💫本文内容来自某机构网课,是我为复试准备的第一个项目 &#…...
)
华为机试真题实战应用【赛题代码篇】-最小传输时延(附python、C++和JAVA代码实现)
目录 问题描述 输入描述: 输出描述: 知识储备 解题思路 思路一...

C++ 运算符重载
(Operator) 加分 减法 []的重载 #include <iostream> using namespace std;class time1 {public:time1(){shi0;fen0;miao0;}time1(int shi, int fen, int miao){this->shi shi;this->fen fen;this->miao miao;}time1 operator (ti…...
vue3学习 【2】vite起步和开发工具基本配置
vite的简介 官方文档 刚起步学习,所以我们只需要按照官方文档的入门流程即可。推荐阅读一下官网的为什么使用vite vite目前需要的node版本是18,可以参考上一篇文章的安装nvm,用来进行多版本的node管理。 vite安装与使用 npm create vitela…...
计算机创新协会冬令营——暴力枚举题目06
我给大家第一阶段的最后一道题就到这里了,下次得过段时间了。所以这道题简单一点。但是足够经典 下述题目描述和示例均来自力扣:两数之和 题目描述 给定一个整数数组 nums 和一个整数目标值 target,请你在该数组中找出 和为目标值 target …...

单片机快速入门
参考连接: 安装MinGW-64(在win10上搭建C/C开发环境)https://zhuanlan.zhihu.com/p/85429160MinGW-64; 链接:https://pan.baidu.com/s/1oE1FmjyK7aJPnDC8vASmCg?pwdy1mz 提取码:y1mz --来自百度网盘超级会员V7的分享C…...
)
Eureka相关问题及答案(2024)
1、什么是Eureka? Eureka是一个由Netflix开发的服务发现(Service Discovery)工具,它是Spring Cloud生态系统中的一个关键组件。服务发现是微服务架构中的一个重要概念,它允许服务实例在启动时注册自己,以便…...

Django 7 实现Web便签
一、效果图 二、会用到的知识 目录结构与URL路由注册request与response对象模板基础与模板继承ORM查询后台管理 三、实现步骤 1. terminal 输入 django-admin startapp the_10回车 2. 注册, 在 tutorial子文件夹settings.py INSTALLED_APPS 中括号添加 "the…...
Jenkins集成部署java项目
文章目录 Jenkins简介安装 Jenkins简介 Jenkins能实时监控集成中存在的错误,提供详细的日志文件和提醒功能,还能用图表的形式形象的展示项目构建的趋势和稳定性。 官网 安装 在官网下载windows版本的Jenkins 但是我点击这里浏览器没有反应࿰…...
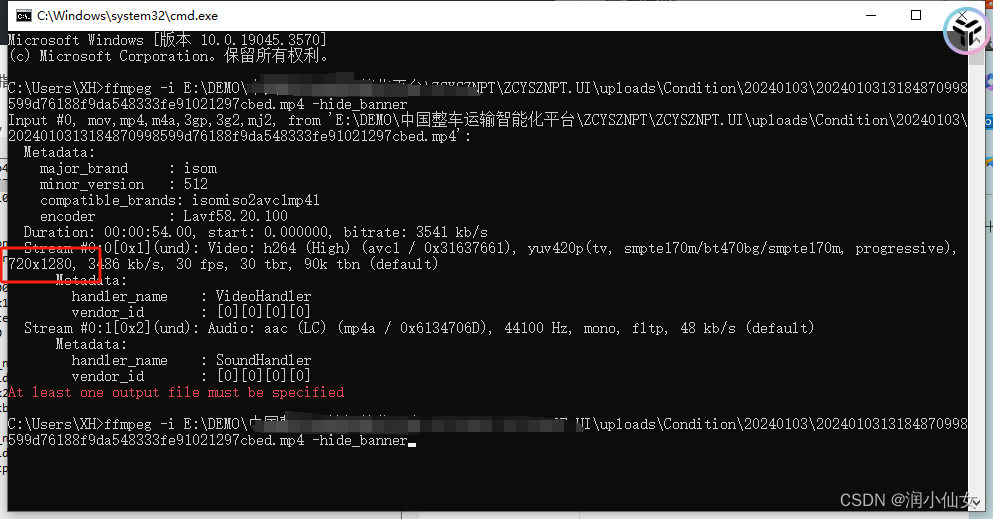
FFmpeg之——获取上传视频的尺寸(长、宽)
获取上传视频的尺寸: 获取视频尺寸通常需要借助第三方库FFmpeg。 首先,确保你的系统中已安装了FFmpeg,并且FFmpeg的可执行文件路径已经添加到你的系统环境变量中。 1.官网下载ffmpeg 进入 链接: ffmpeg官网 网址,点击下载wind…...

Ajax学习
文章目录 AjaxAjax 是什么Ajax 经典应用场景Ajax 原理示意图ajax的异步请求的方法ajax的逻辑:应用实例-验证用户名是否存在思路框架图:需求分析: 到数据库去验证用户名是否可用思路框架图大功告成:使用JQuery-Ajax实现上面相同的需求:Ajax Ajax 是什么 AJAX 即"Async…...

排序算法——关于快速排序的详解
目录 1.基本思想 2.基本原理 2.1划分思想 2.2排序过程 (1)选择基准值 (2)分割过程(Partition) (3)递归排序 (4)合并过程 2.3具体实例 2.4实现代码 2.5关键要…...

序言:《未来已来》
尊敬的读者, 你是否曾经在面对冗长的报告、繁琐的工作、沉重的生活压力时感到困扰,渴望找到一种方式来提升效率,释放压力?你是否曾经在自我创业的道路上,苦于找不到有效的市场营销方式,寻求突破?…...

【Spring实战】22 Spring Actuator 入门
文章目录 1. 定义2. 功能3. 依赖4. 配置5. 常用的应用场景1)环境监控2)运维管理3)性能优化 结论 Spring Actuator 是 Spring 框架的一个模块,为开发人员提供了一套强大的监控和管理功能。本文将深入探讨 Spring Actuator 的定义、…...

JSON安全性
确保JSON处理的安全性是现代Web开发中重要的一环。以下是一些关键的安全实践,用于防止JSON注入攻击以及确保数据在传输过程中的安全性: 1. **验证和清洗输入:** - 在将任何数据写入数据库之前,请确保验证用户输入。对于期望的JSON…...

spring-boot-maven插件repackage(goal)的那些事
前言:在打包Springboot项目成jar包时需要在pom.xml使用spring-boot-maven-plugin来增加Maven功能,在我的上一篇博客<<Maven生命周期和插件的那些事(2021版)>>中已经介绍过Maven和插件的关系,在此不再赘述&…...

ubuntu的boot分区被删除恢复
在鼓捣黑苹果的时候,误删了ubuntu的boot分区,进系统的时候出现emergency mode,那么现在来讲讲怎么恢复 首先做一个ubuntu的启动盘,然后进入启动盘的系统选择试用 呼出命令行,然后添加一个源 sudo add-apt-repository…...

【userfaultfd 条件竞争】starCTF2019 - hackme
前言 呜呜呜,这题不难,但是差不多一个多月没碰我的女朋友 kernel pwn 了,对我的 root 宝宝也是非常想念,可惜这题没有找到我的 root 宝宝,就偷了她的 flag。 哎有点生疏了,这题没看出来堆溢出,…...

深度学习中的自动化标签转换:对数据集所有标签做映射转换
在机器学习中,特别是在涉及图像识别或分类的项目中,标签数据的组织和准确性至关重要。本文探讨了一个旨在高效转换标签数据的 Python 脚本。该脚本在需要更新或更改类标签的场景中特别有用,这是正在进行的机器学习项目中的常见任务。我们将逐…...
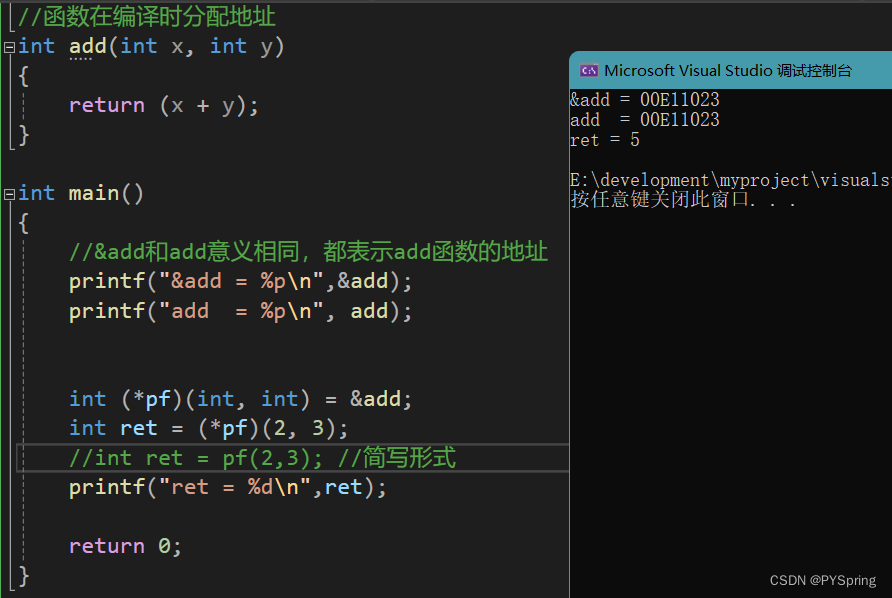
c语言-函数指针
目录 前言一、函数指针1.1 函数指针定义1.2 函数指针调用函数1.3 函数指针代码分析 总结 前言 本篇文章介绍c语言中的函数指针以及函数指针的应用。 一、函数指针 函数指针:指向函数的指针。 函数在编译时分配地址。 &函数名 和 函数名代表的意义相同…...

IDEA运行Tomcat出现乱码问题解决汇总
最近正值期末周,有很多同学在写期末Java web作业时,运行tomcat出现乱码问题,经过多次解决与研究,我做了如下整理: 原因: IDEA本身编码与tomcat的编码与Windows编码不同导致,Windows 系统控制台…...

Golang dig框架与GraphQL的完美结合
将 Go 的 Dig 依赖注入框架与 GraphQL 结合使用,可以显著提升应用程序的可维护性、可测试性以及灵活性。 Dig 是一个强大的依赖注入容器,能够帮助开发者更好地管理复杂的依赖关系,而 GraphQL 则是一种用于 API 的查询语言,能够提…...

Keil 中设置 STM32 Flash 和 RAM 地址详解
文章目录 Keil 中设置 STM32 Flash 和 RAM 地址详解一、Flash 和 RAM 配置界面(Target 选项卡)1. IROM1(用于配置 Flash)2. IRAM1(用于配置 RAM)二、链接器设置界面(Linker 选项卡)1. 勾选“Use Memory Layout from Target Dialog”2. 查看链接器参数(如果没有勾选上面…...

Linux云原生安全:零信任架构与机密计算
Linux云原生安全:零信任架构与机密计算 构建坚不可摧的云原生防御体系 引言:云原生安全的范式革命 随着云原生技术的普及,安全边界正在从传统的网络边界向工作负载内部转移。Gartner预测,到2025年,零信任架构将成为超…...

Springboot社区养老保险系统小程序
一、前言 随着我国经济迅速发展,人们对手机的需求越来越大,各种手机软件也都在被广泛应用,但是对于手机进行数据信息管理,对于手机的各种软件也是备受用户的喜爱,社区养老保险系统小程序被用户普遍使用,为方…...

【Go语言基础【12】】指针:声明、取地址、解引用
文章目录 零、概述:指针 vs. 引用(类比其他语言)一、指针基础概念二、指针声明与初始化三、指针操作符1. &:取地址(拿到内存地址)2. *:解引用(拿到值) 四、空指针&am…...

使用Spring AI和MCP协议构建图片搜索服务
目录 使用Spring AI和MCP协议构建图片搜索服务 引言 技术栈概览 项目架构设计 架构图 服务端开发 1. 创建Spring Boot项目 2. 实现图片搜索工具 3. 配置传输模式 Stdio模式(本地调用) SSE模式(远程调用) 4. 注册工具提…...

Unity UGUI Button事件流程
场景结构 测试代码 public class TestBtn : MonoBehaviour {void Start(){var btn GetComponent<Button>();btn.onClick.AddListener(OnClick);}private void OnClick(){Debug.Log("666");}}当添加事件时 // 实例化一个ButtonClickedEvent的事件 [Formerl…...

MySQL:分区的基本使用
目录 一、什么是分区二、有什么作用三、分类四、创建分区五、删除分区 一、什么是分区 MySQL 分区(Partitioning)是一种将单张表的数据逻辑上拆分成多个物理部分的技术。这些物理部分(分区)可以独立存储、管理和优化,…...
)
安卓基础(Java 和 Gradle 版本)
1. 设置项目的 JDK 版本 方法1:通过 Project Structure File → Project Structure... (或按 CtrlAltShiftS) 左侧选择 SDK Location 在 Gradle Settings 部分,设置 Gradle JDK 方法2:通过 Settings File → Settings... (或 CtrlAltS)…...
