【TypeScript】声明文件
一、定义
- TypeScript 的声明文件包含 .d.ts 扩展名,并用于为 TypeScript 提供关于 JavaScript 代码的类型信息
- 这些文件通常定义了接口、类型别名、类等,但并不包含实际的执行代码
- 当你使用 JavaScript 库或框架时,声明文件就显得非常有用,因为它们帮助 TypeScript 理解库中对象的类型,以便于提供代码补全、类型检查和其他智能支持。
二、声明文件的使用
声明文件的一个用途是描述不是用 TypeScript 编写的 JavaScript 库的形状
例如:
如果你有一个名为 myLib.js 的简单 JavaScript 库,那么相应的声明文件 myLib.d.ts 会这样:
// myLib.d.ts
declare function myFunction(a: number): string;
declare class MyClass {constructor(s: string);myMethod(): number;
}
现在通过 myLib.d.ts 文件,TypeScript 编译器和编辑器就可以知道 myFunction 和 MyClass 的类型。在使用它们的 TypeScript 文件中,你可以直接引用这些声明:
// main.ts
/// <reference path="myLib.d.ts" />let result: string = myFunction(5);
let myObject: MyClass = new MyClass("Hello");
三、声明模块
在第三方 JavaScript 库的声明中,你经常会看到模块被声明的样子。
通过声明模块,你可以导入一个模块并获得 TypeScript 类型的好处,就像这样:
// node_modules/@types/jquery/index.d.ts
declare module 'jquery' {export function $(selector: string): any;
}// 使用时
import $ = require('jquery');
$('my-selector').doSomething();
四、DefinitelyTyped 和 @types
很多流行的 JavaScript 库在 DefinitelyTyped 仓库中都有对应的 .d.ts 类型声明文件,这使得在 TypeScript 项目中使用它们变得非常容易。你只需要运行 npm install @types/{library-name} 就能安装相应的类型定义包。
例如,如果需要使用 lodash 库,你可以安装类型包如下:
npm install --save @types/lodash
然后在代码中这样使用:
import _ from 'lodash';
_.padStart("Hello TypeScript!", 20, " ");
相关文章:

【TypeScript】声明文件
一、定义 TypeScript 的声明文件包含 .d.ts 扩展名,并用于为 TypeScript 提供关于 JavaScript 代码的类型信息这些文件通常定义了接口、类型别名、类等,但并不包含实际的执行代码当你使用 JavaScript 库或框架时,声明文件就显得非常有用&…...
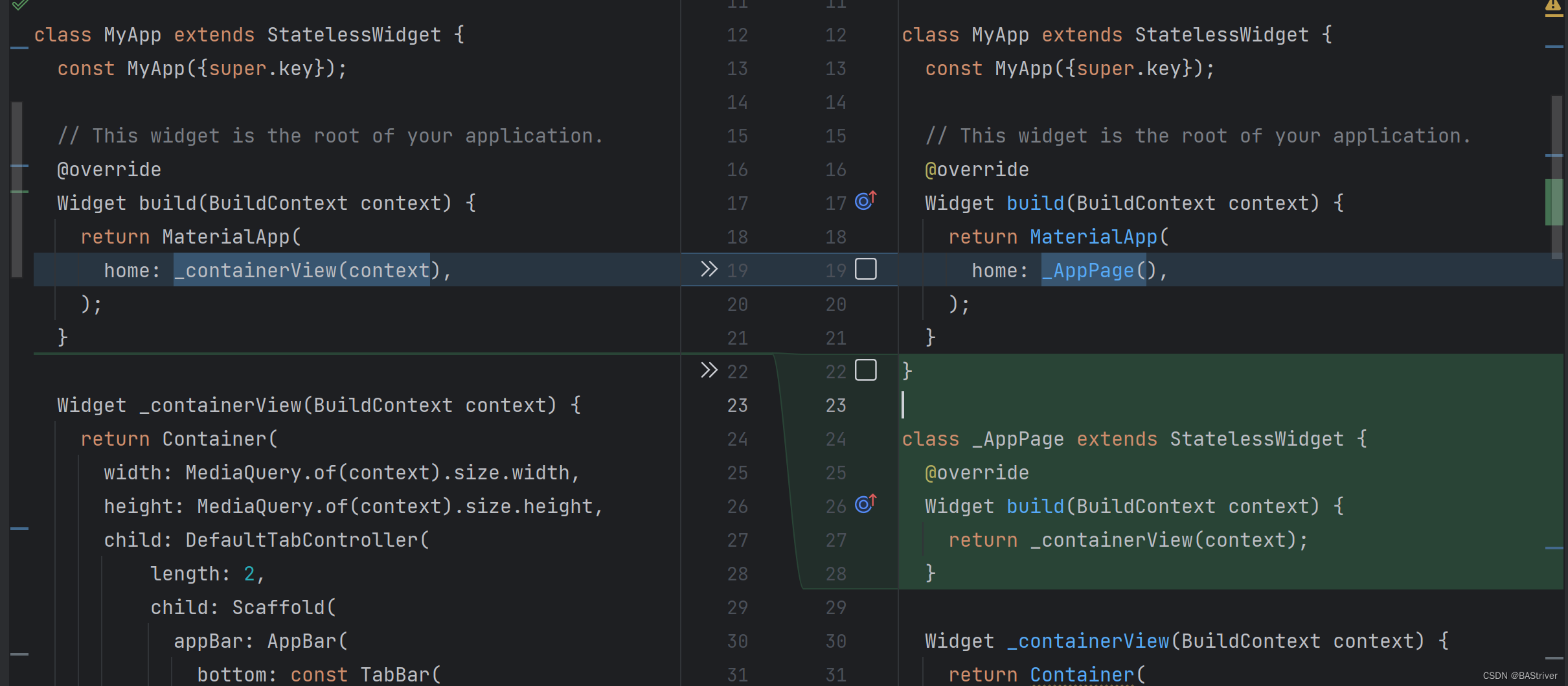
基于Flutter构建小型新闻App
目录 1. 概述 1.1 功能概述 1.2 技术准备 1.3 源码地址 2. App首页 2.1 pubspec依赖 2.2 热门首页组件 2.2.1 DefaultTabController 2.2.2 Swiper 2.3 新闻API数据访问 2.4 热门首页效果图 3. 新闻分类 3.1 GestureDetector 3.2 新闻分类效果图 4. 收藏功能 4…...

利用python将excel文件转成txt文件,再将txt文件上传hdfs,最后传入hive中
将excel文件转成txt文件,再将txt文件上传hdfs,最后传入hive中 注意的点 (1)先判断写入的txt文件是否存在,如果不存在就需要创建路径 (2)如果txt文件已经存在,那么先将对应的文件进行…...
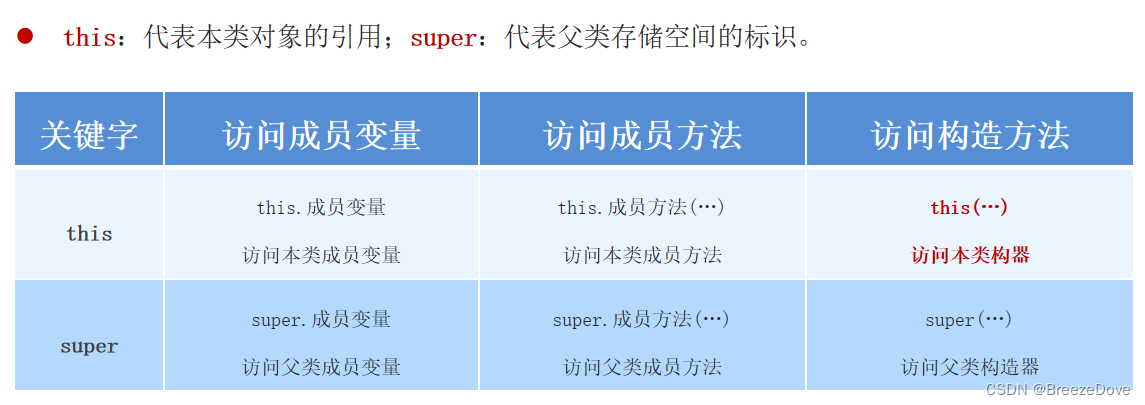
【自学笔记】01Java基础-07面向对象基础-02继承
记录学习Java基础中有关继承、方法重写、构造器调用的基础知识,学习继承之前建议学习static关键字的内容【自学笔记】01Java基础-09Java关键字详解 1 继承概述 1.1 什么是继承? 1.2 继承的特点 子类可以继承父类的属性和行为,但是子类不能…...

二分查找(一)
算法原理 原理:当一个序列有“二段性”的时候,就可以使用二分查找算法。 适用范围:根据规律找一个点,能将这个数组分成两部分,根据规律能有选择性的舍去一部分,进而在另一个部分继续查找。 除了最普通的…...

【华为OD真题 Python】精准核酸检测
文章目录 题目描述输入描述输出描述示例1输入输出说明备注代码实现题目描述 为了达到新冠疫情精准防控的需要,为了避免全员核酸检测带来的浪费,需要精准圈定可能被感染的人群。 现在根据传染病流调以及大数据分析,得到了每个人之间在时间、空间上是否存在轨迹的交叉。 现…...

Springboot使用logback
文章目录 目录 文章目录 前言 一、添加依赖 二、使用步骤 三 、测试使用 总结 前言 Logback 是log4j 框架的作者开发的新一代日志框架,它效率更高、能够适应诸多的运行环境,同时天然支持 SLF4J。 Logback 的定制性更加灵活,同时也是 Sprin…...
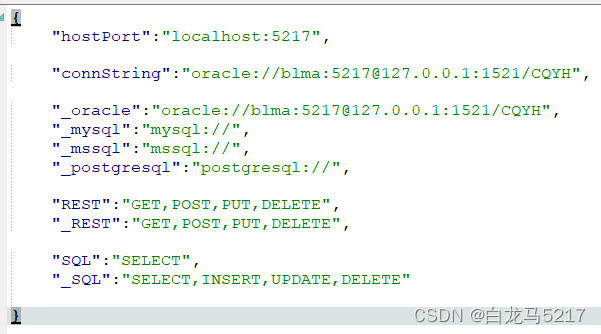
【REST2SQL】03 GO读取JSON文件
REST2SQL需要一些配置信息,用JSON文件保存,比如config.json 1 创建config.json配置文件 {"hostPort":"localhost:5217","connString":"oracle://blma:5217127.0.0.1:1521/CQYH","_oracle":"ora…...
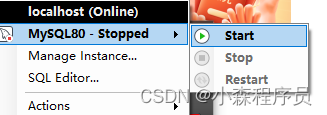
数据库-MySQL 启动方式
以管理员身份运行命令行 或者Shell net start //查看所有服务 net start MYSQL80 //启动服务 net stop MYSQL80 //停止服务完整安装MySQL社区版本的 会有这个 启动服务 停止服务 重启服务...

YAML使用
yaml yaml是类型aml,json的标记性语言,它强调以数据为中心 yaml的语法主要是如下几个: 大小写敏感 使用缩进表示层级关系 缩进不允许使用tab、只允许空格(低版本限制,高版本不限制) 缩进时空格数不重要&a…...
)
读书之深入理解ffmpeg_简单笔记2(初步)
再回看第一遍通读后的笔记,感觉还有很多的细节需要一一攻克,。 mp4的封装格式,解析方式。 flv的封装格式,解析方式。 ts的封装格式,解析方式。 第四章 封装和解封装 4.2 视频文件转flv (头文件和文件内容࿰…...

ELK+kafka+filebeat企业内部日志分析系统搭建
看上面的拓扑图,我们至少准备七台机器进行下面的实验项目。 机器主要作用分布如下: 三台安装elasticsearch来搭建ES集群实现高可用,其他机器就依次安装filebeat,kafka,logstash和kibana软件 一、部署elasticsearch来搭建ES集群 1.安装jdk 由于ES运行…...
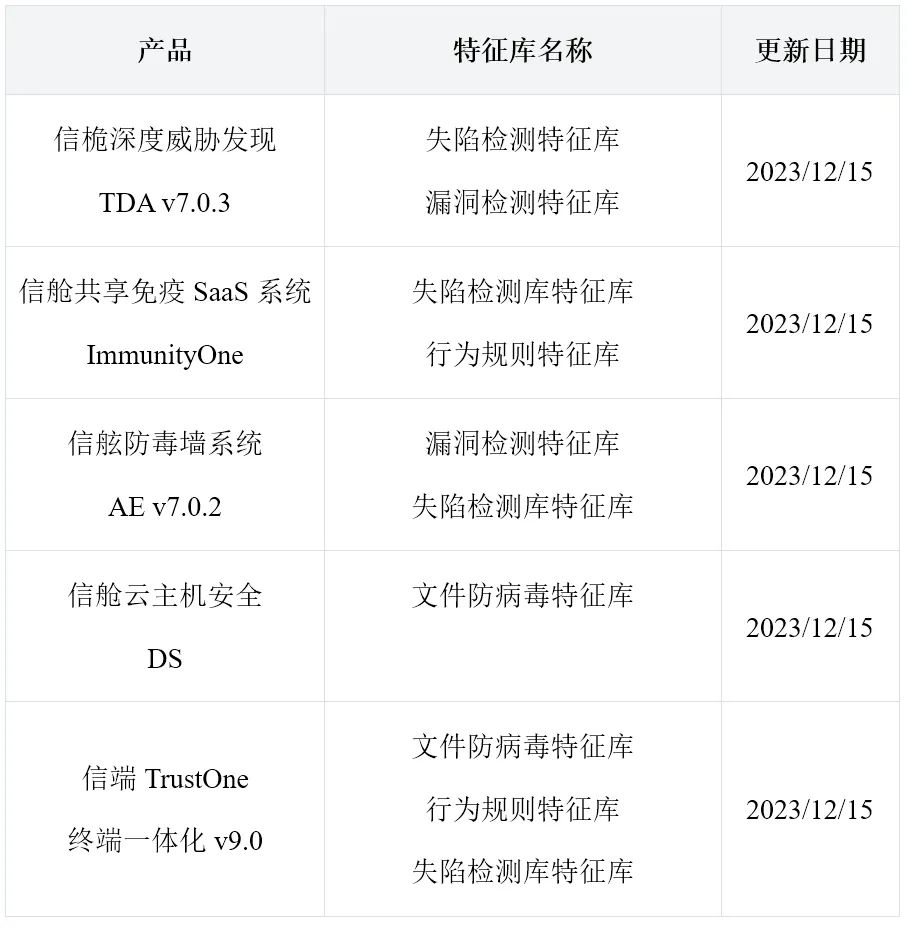
勒索检测能力升级,亚信安全发布《勒索家族和勒索事件监控报告》
评论员简评 近期(12.08-12.14)共发生勒索事件119起,相较之前呈现持平趋势。 与上周相比,近期仍然流行的勒索家族为lockbit3和8base。在涉及的勒索家族中,活跃程度Top5的勒索家族分别是:lockbit3、siegedsec、dragonforce、8base和…...

编译原理复习的有用链接
2024年1月7日,考完编译原理,是时候和考试时候的她说再见了,整理一些收藏夹里的链接和思考吧 实验看这里: 编译原理_HNU岳麓山大小姐的博客-CSDN博客 课后习题看这里: 编译原理作业答案github LL1文法复习 [编译原…...
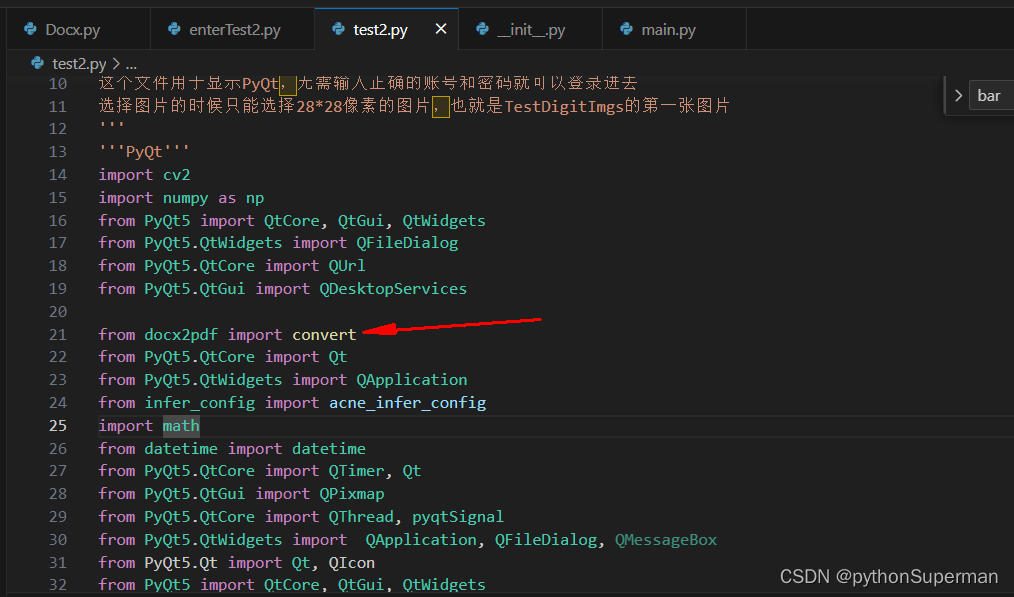
不带控制器打包exe,转pdf文件时失败的原因
加了注释的两条代码后,控制器会显示一个docx转pdf的进度条。这个进度条需要控制器的实现,如果转exe不带控制器的话,当点击转换为pdf的按钮就会导致程序出错和闪退。 __init__.py文件的入口...

Python 注释的方法
在Python中,有两种常见的注释方法: 单行注释:使用#符号来注释一行代码。在#符号后面的内容将被视为注释,不会被解释器执行,如: # 这是一个单行注释 print(hello world!) # 打印字符串多行注释࿱…...

webman插件创建
webman插件创建 介绍 应用插件实际上是一个完整的应用,它能以插件的形式安装到主项目中,使主项目快速获得某个模块功能。 例如:主项目需要一个问答系统,则可以安装一个问答应用插件,需要一个商城系统,则安…...
大模型迎来“AppStore时刻”,OpenAI给2024的新想象
一夜之间,OpenAI公布了多个重磅消息,引发市场关注。 钛媒体App 1月5日消息,今晨,OpenAI公司向所有GPT开发者们发布一封邮件称,下周将上线自定义的“GPT Store”商店,这有望推动ChatGPT开发者生态不断完善。…...

ubuntu解决在pycharm上使用jupyter无法导入虚拟环境中的包的问题
ubuntu解决在pycharm上使用jupyter无法导入虚拟环境中的包的问题 根本原因是jupyter 没有和他对应的kernel 需要先使用命令行建立kernel 下载ipykernel pip install ipykernel 首先激活conda conda activate然后添加你的kernel到虚拟环境 python -m ipykernel install -…...
探索2024年软件测试的几大主导趋势
进入2024年,考虑影响测试环境的问题至关重要。这种思考将成为团队了解主要瓶颈和实现当今不断提高的期望的首要因素。 01 了解关键测试瓶颈 毋庸置疑,现代团队需要不断创新、适应和拥抱最新趋势,以保持竞争力并提供以客户为中心的解决方案。尽…...

pam_env.so模块配置解析
在PAM(Pluggable Authentication Modules)配置中, /etc/pam.d/su 文件相关配置含义如下: 配置解析 auth required pam_env.so1. 字段分解 字段值说明模块类型auth认证类模块,负责验证用户身份&am…...

对WWDC 2025 Keynote 内容的预测
借助我们以往对苹果公司发展路径的深入研究经验,以及大语言模型的分析能力,我们系统梳理了多年来苹果 WWDC 主题演讲的规律。在 WWDC 2025 即将揭幕之际,我们让 ChatGPT 对今年的 Keynote 内容进行了一个初步预测,聊作存档。等到明…...

React19源码系列之 事件插件系统
事件类别 事件类型 定义 文档 Event Event 接口表示在 EventTarget 上出现的事件。 Event - Web API | MDN UIEvent UIEvent 接口表示简单的用户界面事件。 UIEvent - Web API | MDN KeyboardEvent KeyboardEvent 对象描述了用户与键盘的交互。 KeyboardEvent - Web…...

第25节 Node.js 断言测试
Node.js的assert模块主要用于编写程序的单元测试时使用,通过断言可以提早发现和排查出错误。 稳定性: 5 - 锁定 这个模块可用于应用的单元测试,通过 require(assert) 可以使用这个模块。 assert.fail(actual, expected, message, operator) 使用参数…...

Robots.txt 文件
什么是robots.txt? robots.txt 是一个位于网站根目录下的文本文件(如:https://example.com/robots.txt),它用于指导网络爬虫(如搜索引擎的蜘蛛程序)如何抓取该网站的内容。这个文件遵循 Robots…...

WordPress插件:AI多语言写作与智能配图、免费AI模型、SEO文章生成
厌倦手动写WordPress文章?AI自动生成,效率提升10倍! 支持多语言、自动配图、定时发布,让内容创作更轻松! AI内容生成 → 不想每天写文章?AI一键生成高质量内容!多语言支持 → 跨境电商必备&am…...

Python如何给视频添加音频和字幕
在Python中,给视频添加音频和字幕可以使用电影文件处理库MoviePy和字幕处理库Subtitles。下面将详细介绍如何使用这些库来实现视频的音频和字幕添加,包括必要的代码示例和详细解释。 环境准备 在开始之前,需要安装以下Python库:…...

PAN/FPN
import torch import torch.nn as nn import torch.nn.functional as F import mathclass LowResQueryHighResKVAttention(nn.Module):"""方案 1: 低分辨率特征 (Query) 查询高分辨率特征 (Key, Value).输出分辨率与低分辨率输入相同。"""def __…...

人工智能--安全大模型训练计划:基于Fine-tuning + LLM Agent
安全大模型训练计划:基于Fine-tuning LLM Agent 1. 构建高质量安全数据集 目标:为安全大模型创建高质量、去偏、符合伦理的训练数据集,涵盖安全相关任务(如有害内容检测、隐私保护、道德推理等)。 1.1 数据收集 描…...

DBLP数据库是什么?
DBLP(Digital Bibliography & Library Project)Computer Science Bibliography是全球著名的计算机科学出版物的开放书目数据库。DBLP所收录的期刊和会议论文质量较高,数据库文献更新速度很快,很好地反映了国际计算机科学学术研…...
