uView-UI v2.x常见问题整理
相关文章：
uView-UI v2.x常见问题整理
为了更好的给大家提供 uView UI 的技术支持，uView UI 团队整理常见问题文档，大家可以阅读查找常见的问题解决办法。 uView 2.x 文档 https://www.uviewui.com uView 1.x 文档 https://v1.uviewui.com uView UI uni-app 主页 DCloud 插件市场 uVie…...
MBTI职业性格测试 28题（免费版）
MBTI职业性格测试概述 MBTI是现在国际上最为流行的测试工具，利用MBTI职业性格测试，可以清楚地找到自己的性格特点以及兴趣爱好，方便于对职业进行规划、以及改善人际关系。其主要应用心理学常识对个性做出判断，提炼出动力、信息收…...
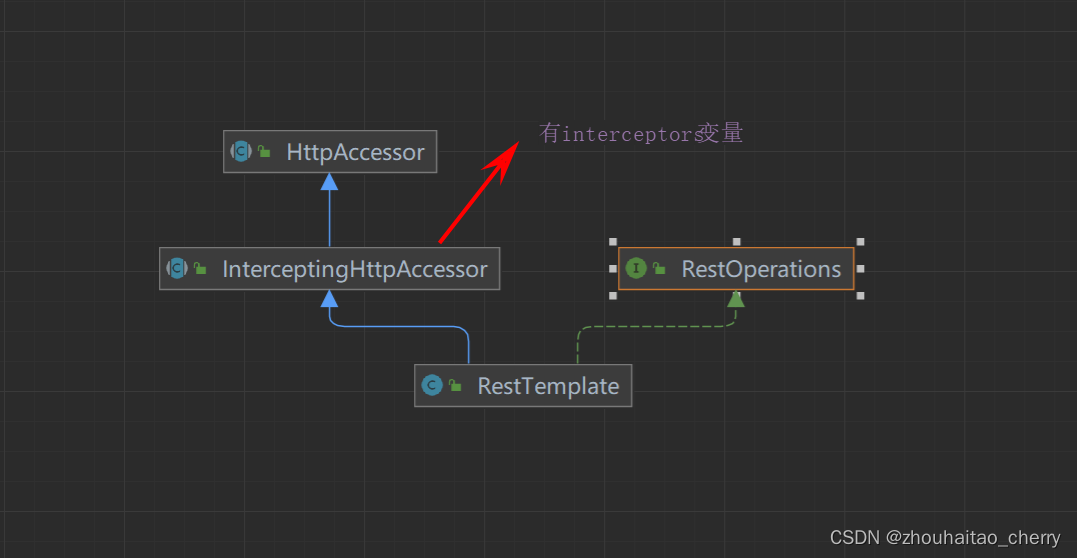
Springcloud 微服务实战笔记 Ribbon
使用 Configurationpublic class CustomConfiguration {BeanLoadBalanced // 开启负载均衡能力public RestTemplate restTemplate() {return new RestTemplate();}}可看到使用Ribbon，非常简单，只需将LoadBalanced注解加在RestTemplate的Bean上࿰…...
CSS基础笔记-04cascade-specificity-inheritance
CSS基础笔记系列 《CSS基础笔记-01CSS概述》《CSS基础笔记-02动画》CSS基础笔记-03选择器 前言 Cascading Style Sheets，关键就在于这个cascading，对于这个术语理解，感觉对于我这种CSS新手有点儿不太friendly。本文记录下我对这个术语的理…...
Spring应用的部署与管理
一、前言 部署是将开发好的应用发布到服务器上，使其能够被用户访问的关键步骤。Spring框架提供了灵活的部署选项，本文将介绍Spring应用的常见部署方式和一些建议，帮助开发者顺利将应用投放到生产环境。 二、传统部署方式：WAR包 传…...
B端产品经理学习-需求挖掘
B端产品需求挖掘 目录 识别和管理干系人 决策人和负责人需求挖掘 针对用户进行需求挖掘 用户访谈结果整理 B端产品的需求来源是非常复杂的，要考虑多个方面；如果你是一个通用性的产品，要考虑市场、自身优劣势、干系人。而定制型B端产品会…...
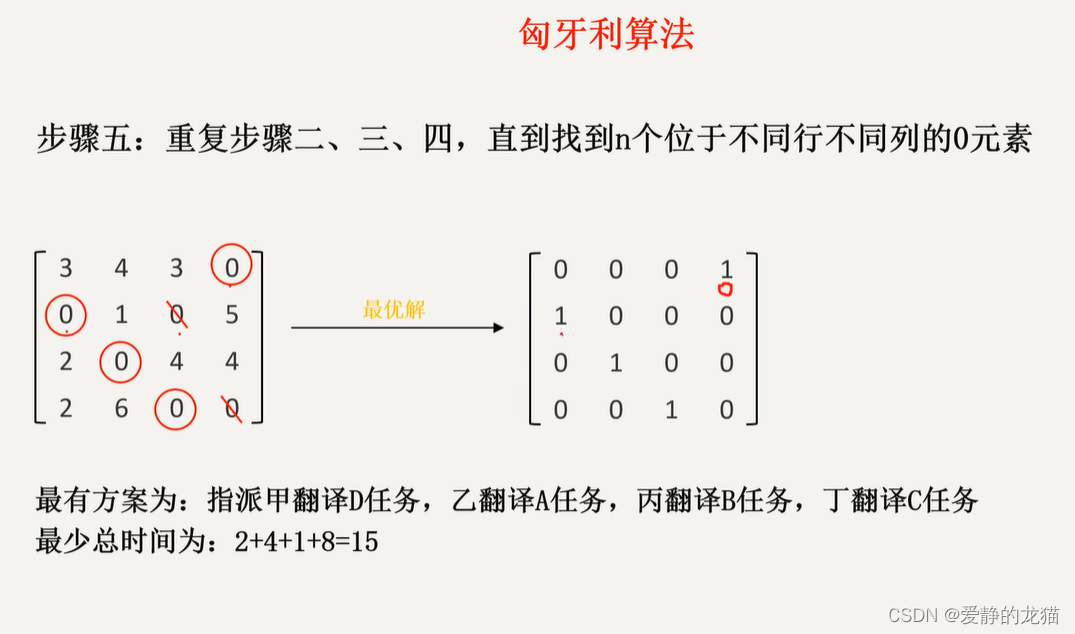
整数规划基本原理
1.1 定义 规划中的变量（部分或全部）限制为整数时，称为整数规划。若在线性规划模型中，变量限制为整数，则称为整数线性规划。目前所流行的求解整数规划的方法，往往只适用于整数线性规划。目前还没有一种方法…...
秋招复习之堆
目录 前言 堆 堆的常用操作 堆的实现（大根堆） 1. 堆的存储与表示 2. 访问堆顶元素 3. 元素入堆 4. 堆顶元素出堆 Top-k 问题 方法一：遍历选择 方法二：排序 方法三：堆 总结 前言 秋招复习之堆。 堆 「堆 heap…...
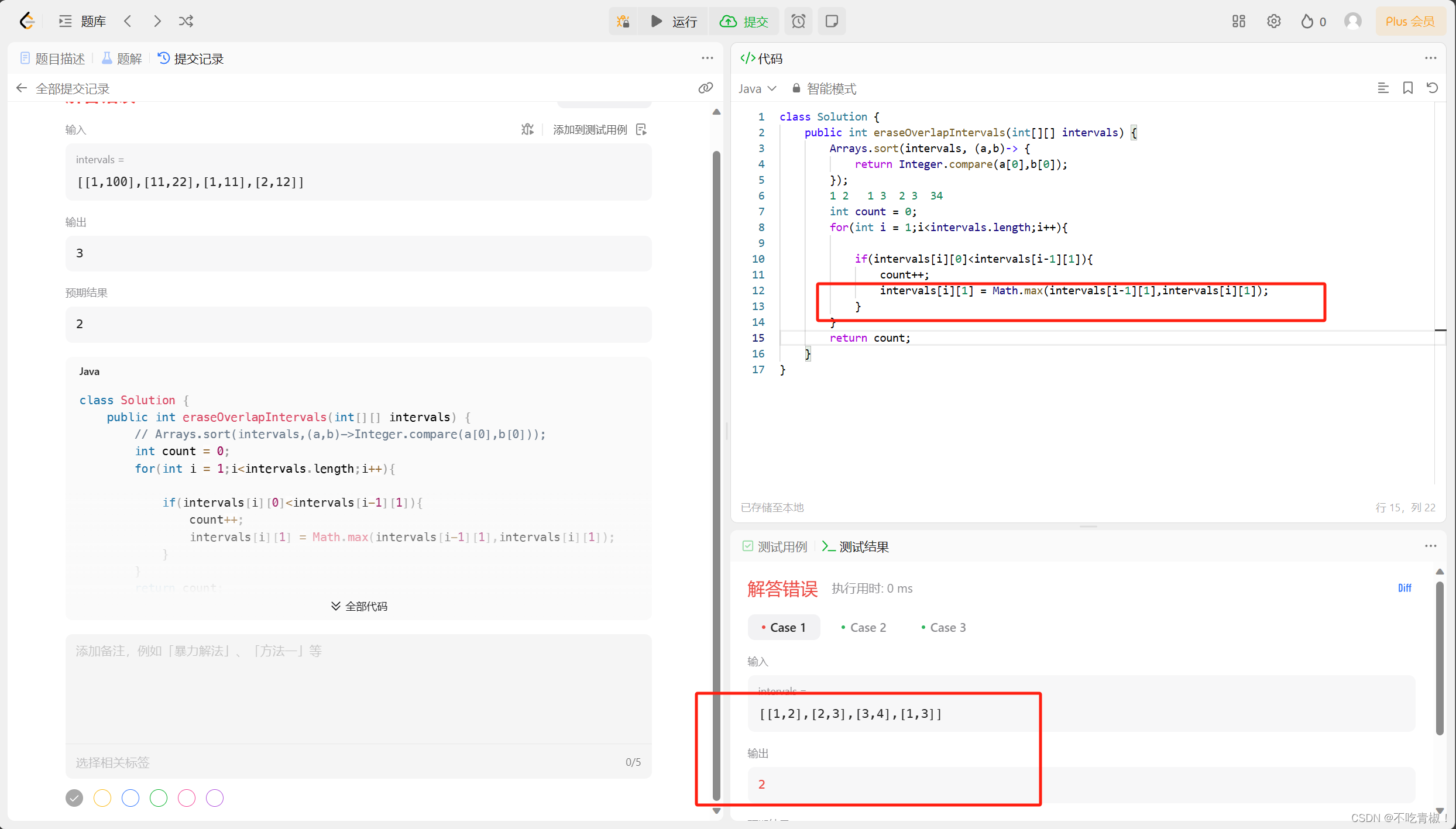
算法训练营Day36(贪心-重叠区间）
都算是 重叠区间 问题，大家可以好好感受一下。 都属于那种看起来好复杂，但一看贪心解法，惊呼：这么巧妙！ 还是属于那种，做过了也就会了，没做过就很难想出来。 不过大家把如下三题做了之后&#…...
如何利用Oracle官方网站不登录账号下载和安装非最新版本的JDK（版本自由选择）
一、JDK概述 JDK（Java Development Kit）是Java开发工具集，是针对Java编程语言的软件开发环境。它包含了Java编译器、JRE（Java运行时环境）以及其他一些用于开发、调试和测试Java应用程序的工具，是Java开发人…...
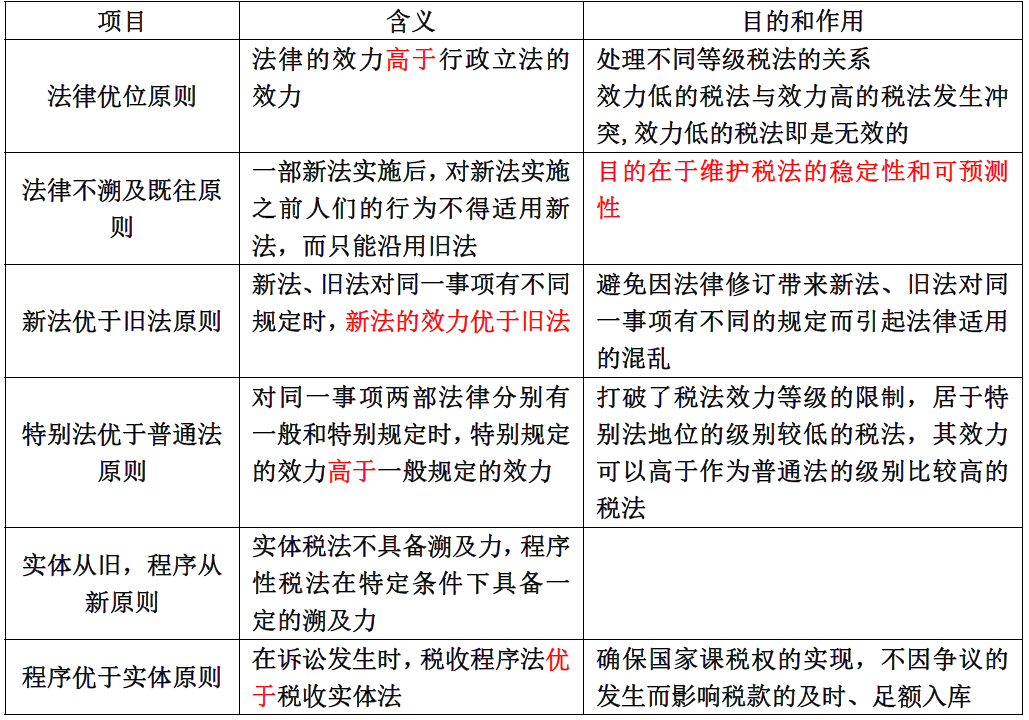
税法相关的基础知识
文章目录 税法原则1.税法基本原则2.税法适用原则 来和大家聊聊税法相关的基础知识 税法原则 1.税法基本原则 2.税法适用原则...
ListNode 2487. 从链表中移除节点，单调栈的应用
一、题目 1、题目描述 给你一个链表的头节点 head 。 移除每个右侧有一个更大数值的节点。 返回修改后链表的头节点 head 。 2、接口描述 /*** Definition for singly-linked list.* struct ListNode {* int val;* ListNode *next;* ListNode() : val(0), next(nu…...
vue3中pdf打印问题处理
1 get请求参数问题 之前的请求是post得不到参数，今天发现的问题很奇怪，从前端进入网关，网关居然得不到参数。 前端代码 const print () > {let linkUrlStr proxy.$tool.getUrlStr(proxy.$api.invOrder.psiInvOrder.printSalOutstock,{a…...
如何向嵌入式设备中添加tcpdump工具
说明：tcpdump是一个在网络设备调试中一个非常重要的工具，它并不像hexdump等工具集成在busybox里面，也不像其他的软件一样只需要依赖linux标准的库就可以实现，它需要pcap相关的库和加密的相关库。 本文主要是基于realtek 83系列的…...
伦茨科技Apple Find My认证芯片-ST17H6x芯片
深圳市伦茨科技有限公司（以下简称“伦茨科技”）发布ST17H6x Soc平台。成为继Nordic之后全球第二家取得Apple Find My「查找」认证的芯片厂家，该平台提供可通过Apple Find My认证的Apple查找（Find My）功能集成解决方案。…...
uni-app 前后端调用实例 基于Springboot 数据列表显示实现
锋哥原创的uni-app视频教程： 2023版uniapp从入门到上天视频教程(Java后端无废话版)，火爆更新中..._哔哩哔哩_bilibili2023版uniapp从入门到上天视频教程(Java后端无废话版)，火爆更新中...共计23条视频，包括：第1讲 uni…...
python渗透工具编写学习笔记：10、网络爬虫基础/多功能编写
目录 前言 10.1 概念 10.2 调度器/解析器 10.3 存储器/去重器 10.4 日志模块 10.5 反爬模块 10.6 代理模块 前言 在渗透工具中，网络爬虫有着不可忽视的作用，它能够快速而精准的搜寻、提取我们所需要的信息并按照我们所需要的格式排列，…...
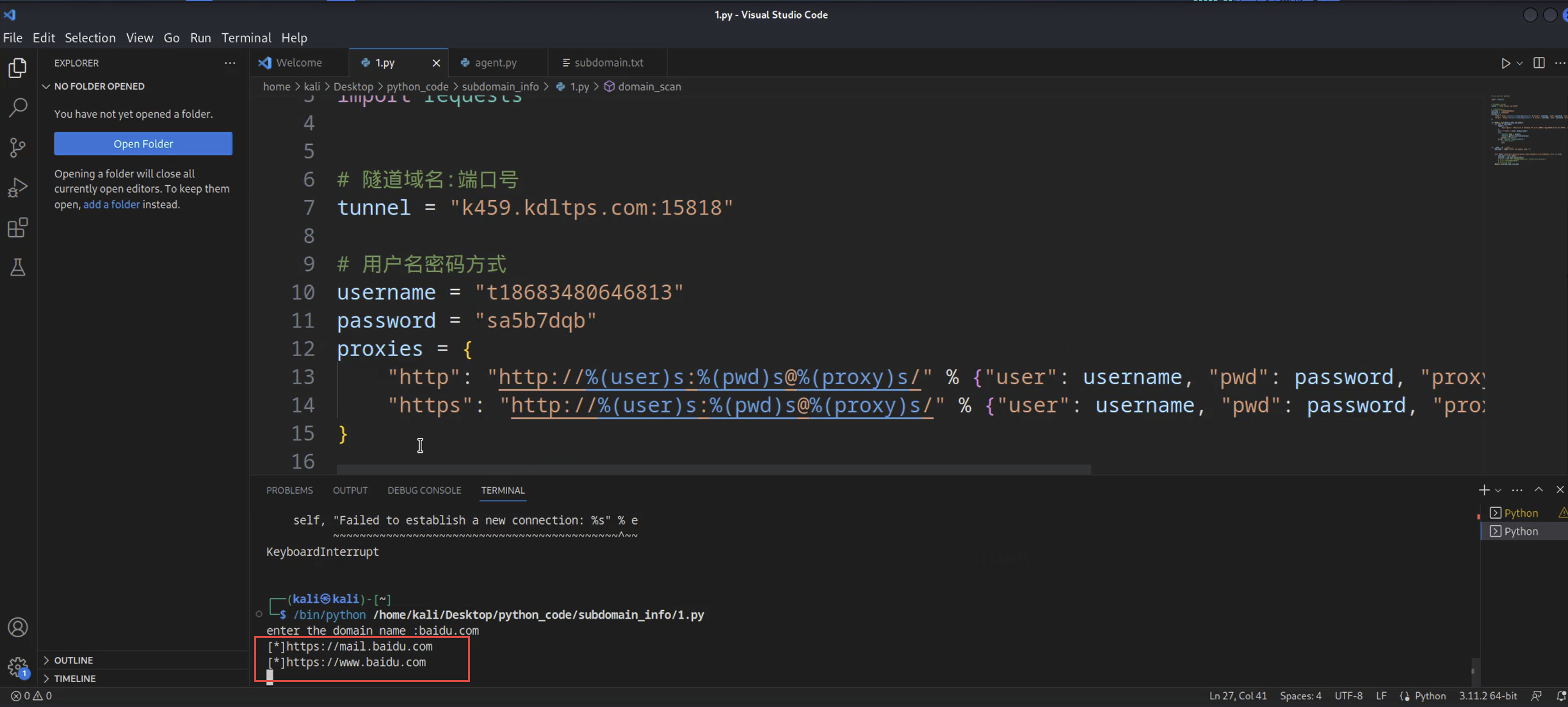
Python武器库开发-武器库篇之子域名扫描器开发(四十一)
Python武器库开发-武器库篇之子域名扫描器开发(四十一) 在我们做红队攻防或者渗透测试的过程中，信息收集往往都是第一步的，有人说：渗透的本质就是信息收集，前期好的信息收集很大程度上决定了渗透的质量和攻击面，本文将…...
通俗易懂的15个Java Lambda表达式案例
文章目录 1. **实现Runnable接口**：2. **事件监听器**（如Swing中的ActionListener）：3. **集合遍历**（使用forEach方法）：4. **过滤集合**（使用Stream API）：5. …...
十七：爬虫-JS逆向（上）
1、什么是JS、JS反爬是什么？JS逆向是什么? JS:JS全称JavaScript是互联网上最流行的脚本语言，这门语言可用于HTML 和 web，更可广泛用于服务器、PC、笔记本电脑、平板电脑和智能手机等设备。JavaScript 是一种轻量级的编程语言。JavaScript 是…...
多场景 OkHttpClient 管理器 - Android 网络通信解决方案
下面是一个完整的 Android 实现，展示如何创建和管理多个 OkHttpClient 实例，分别用于长连接、普通 HTTP 请求和文件下载场景。 <?xml version"1.0" encoding"utf-8"?> <LinearLayout xmlns:android"http://schemas…...
VTK如何让部分单位不可见
最近遇到一个需求，需要让一个vtkDataSet中的部分单元不可见，查阅了一些资料大概有以下几种方式 1.通过颜色映射表来进行，是最正规的做法 vtkNew<vtkLookupTable> lut; //值为0不显示，主要是最后一个参数，透明度…...
从零实现STL哈希容器：unordered_map/unordered_set封装详解
本篇文章是对C学习的STL哈希容器自主实现部分的学习分享 希望也能为你带来些帮助~ 那咱们废话不多说，直接开始吧！ 一、源码结构分析 1. SGISTL30实现剖析 // hash_set核心结构 template <class Value, class HashFcn, ...> class hash_set {ty…...
OPenCV CUDA模块图像处理-----对图像执行 均值漂移滤波（Mean Shift Filtering）函数meanShiftFiltering()
操作系统：ubuntu22.04 OpenCV版本：OpenCV4.9 IDE:Visual Studio Code 编程语言：C11 算法描述 在 GPU 上对图像执行 均值漂移滤波（Mean Shift Filtering），用于图像分割或平滑处理。 该函数将输入图像中的…...
在Ubuntu24上采用Wine打开SourceInsight
1. 安装wine sudo apt install wine 2. 安装32位库支持，SourceInsight是32位程序 sudo dpkg --add-architecture i386 sudo apt update sudo apt install wine32:i386 3. 验证安装 wine --version 4. 安装必要的字体和库（解决显示问题） sudo apt install fonts-wqy…...
AGain DB和倍数增益的关系
我在设置一款索尼CMOS芯片时，Again增益0db变化为6DB，画面的变化只有2倍DN的增益，比如10变为20。 这与dB和线性增益的关系以及传感器处理流程有关。以下是具体原因分析： 1. dB与线性增益的换算关系 6dB对应的理论线性增益应为&…...
三分算法与DeepSeek辅助证明是单峰函数
前置 单峰函数有唯一的最大值，最大值左侧的数值严格单调递增，最大值右侧的数值严格单调递减。 单谷函数有唯一的最小值，最小值左侧的数值严格单调递减，最小值右侧的数值严格单调递增。 三分的本质 三分和二分一样都是通过不断缩…...
QT开发技术【ffmpeg + QAudioOutput】音乐播放器
一、 介绍 使用ffmpeg 4.2.2 在数字化浪潮席卷全球的当下，音视频内容犹如璀璨繁星，点亮了人们的生活与工作。从短视频平台上令人捧腹的搞笑视频，到在线课堂中知识渊博的专家授课，再到影视平台上扣人心弦的高清大片，音…...
pgsql：还原数据库后出现重复序列导致“more than one owned sequence found“报错问题的解决
问题： pgsql数据库通过备份数据库文件进行还原时，如果表中有自增序列，还原后可能会出现重复的序列，此时若向表中插入新行时会出现“more than one owned sequence found”的报错提示。 点击菜单“其它”-》“序列”，…...
2025-05-08-deepseek本地化部署
title: 2025-05-08-deepseek 本地化部署 tags: 深度学习 程序开发 2025-05-08-deepseek 本地化部署 参考博客 本地部署 DeepSeek：小白也能轻松搞定！ 如何给本地部署的 DeepSeek 投喂数据，让他更懂你 [实验目的]：理解系统架构与原…...