逆置算法和数组循环移动算法
元素逆置
- 概述:其实就是将 第一个元素和最后一个元素交换,第二个元素和倒数第二个元素交换,依次到中间位置。
- 用途:可用于数组的移动,字符串反转,链表反转操作,栈和队列反转等操作。
逆置图解

代码
// 逆置元素算法
void Reverse(int R[] , int l , int r){// R 数组,l 左边 r 右边int i , j ,temp;for(i=l , j=r; i < j; i++,j--){ // i < j 不过数组个数是奇数还是偶数都行temp = R[i];R[i] = R[j];R[j] = temp;}
}
注意:逆置算法很简单,但是能延申其他的算法
循环移动算法
- 考研常考的一个算法,结合逆置算法,可进行实现
循环左移(右移)算法
图解
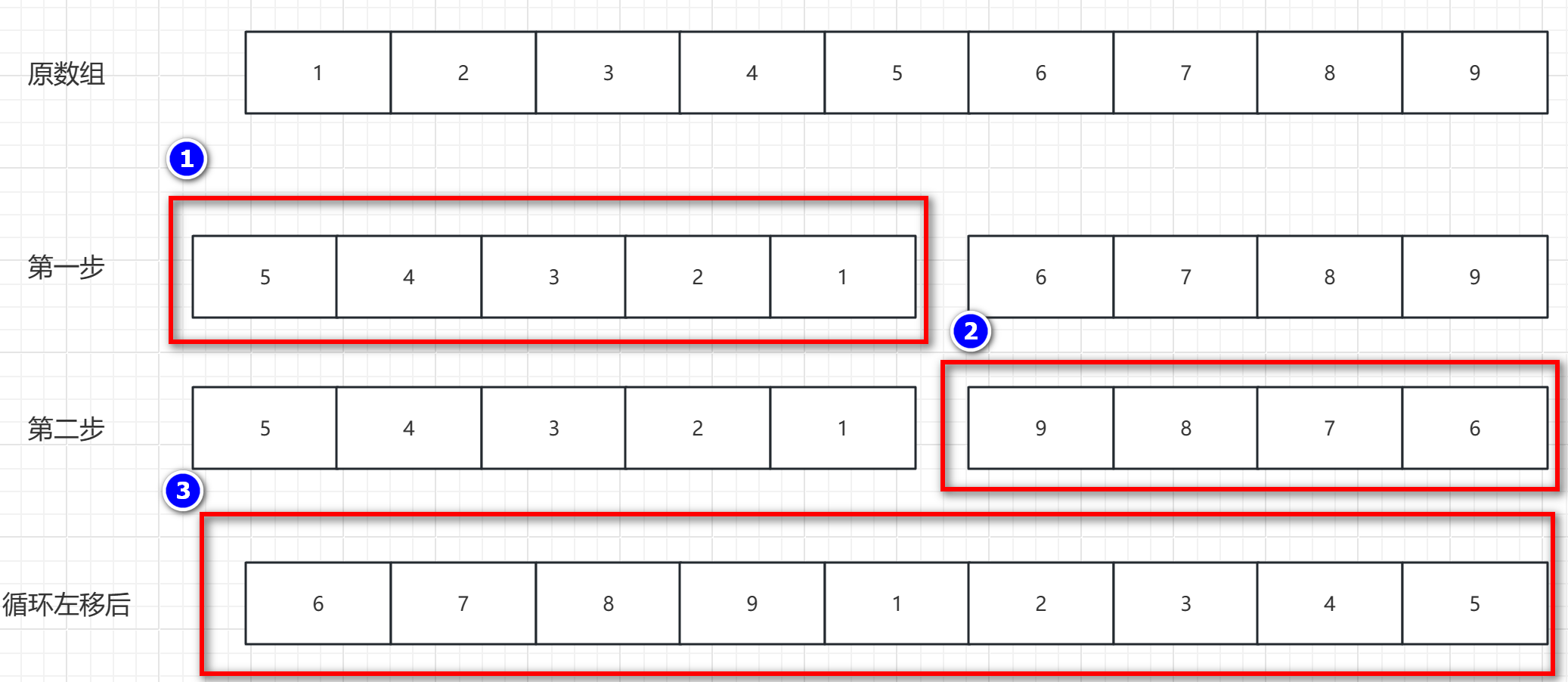
- 第一步:循环左移 p 个元素,就将 数组前 p 个(0~p-1)元素先进行逆置
- 第二步:再将 数组 p-1位置 之后的(n-p)个元素进行逆置
- 第三步:将 整个数组 整体进行逆置,即可得到 循环左移 p 个元素
代码
// 逆置元素算法
void Reverse(int R[] , int l , int r){// R 数组,l 左边 r 右边int i , j ,temp;for(i=l , j=r; i < j; i++,j--){temp = R[i];R[i] = R[j];R[j] = temp;}
}
// 循环左移算法
void LeftMove(int R[] , int n , int p){// r 数组 n 数组元素个数 p 循环左移个数if(p<0 || p>n){cout <<"ERROR"<<endl; }else{Reverse(r , 0 , p-1); // 先逆置前p个Reverse(r , p , n-1); // 再逆置后n-p个Reverse(r , 0 , n-1); // 最后再把所有的都逆置}
}
时间复杂度分析
①:第一行 Reverse 执行频度为:1 + (p-1-0+1)/2
②:第二行 Reverse 执行频度为:1 + (n-1-p+1)/2
③:第三行 Reverse 执行频度为:1 + (n-1-0+1)/2
f(n) = 3 + n
T(n) = O(f(n)) = O(n)
空间复杂度
由于可以看到在 整个算法中,我们只定义了变量,并未定义其他数据结构,也未使用递归,所以空间复杂度是常数级别。为 O(1)
相关文章:

逆置算法和数组循环移动算法
元素逆置 概述:其实就是将 第一个元素和最后一个元素交换,第二个元素和倒数第二个元素交换,依次到中间位置。用途:可用于数组的移动,字符串反转,链表反转操作,栈和队列反转等操作。 逆置图解 …...

【MATLAB】数豆子
Matlab数豆子 创建一个变量来表示豆子的数量。例如,可以使用豆子数量 100;来表示有100颗豆子。 使用disp函数打印出豆子的数量。例如,可以使用disp([目前有 num2str(豆子数量) 颗豆子])来打印出当前豆子的数量。 进行豆子的计数操作。例如,…...

QT C++中调用python脚本时,import第三方库失败问题解决
QT C中调用python脚本时,import第三方库失败问题解决 文章目录 QT C中调用python脚本时,import第三方库失败问题解决前言一、问题复现二、调试过程三、问题解决1 numpy问题解决2 matplotlib问题解决 四、补充说明五、参考资料 前言 项目需要,…...

【AI视野·今日Robot 机器人论文速览 第七十期】Thu, 4 Jan 2024
AI视野今日CS.Robotics 机器人学论文速览 Thu, 4 Jan 2024 Totally 17 papers 👉上期速览✈更多精彩请移步主页 Daily Robotics Papers Many-Objective-Optimized Semi-Automated Robotic Disassembly Sequences Authors Takuya Kiyokawa, Kensuke Harada, Weiwei …...

Flutter中的布局组件介绍及使用
1. 引言 Flutter 是一款由 Google 开发的开源 UI 软件开发工具,可用于在单个代码库中构建漂亮、本机编译的应用程序。在 Flutter 中,布局是构建用户界面的核心部分之一。本文将介绍 Flutter 中的全部布局组件,以及它们的使用方式。 2. 基础…...

【面试高频算法解析】算法练习2 回溯(Backtracking)
前言 本专栏旨在通过分类学习算法,使您能够牢固掌握不同算法的理论要点。通过策略性地练习精选的经典题目,帮助您深度理解每种算法,避免出现刷了很多算法题,还是一知半解的状态 专栏导航 二分查找回溯(Backtracking&…...

认识Git
🌎初识Git 初识Git 什么是Git Git的安装 Centos平台安装Git Ubuntu平台安装Git Git的基本操作 创建远程仓库 配置Git 认识工作区、暂存区与版本库 添加文件到暂存区 将暂存区文件提交至本…...

@RequestParam,@RequestBody和@PathVariable 区别
RequestParam,RequestBody和PathVariable 这三者是spring常见的接受前端数据的注解,那么他们分别是接受什么的前端数据呢? RequestParam:这个注解主要用于处理请求参数,尤其是GET请求中的查询参数和表单参数。它可以用…...

vue3组件传参
1、props: 2、自定义事件子传父 3、mitt任意组件通讯 4、v-model通讯(v-model绑定在组件上) (1)V2中父子组件的v-model通信,限制了popos接收的属性名必须为value和emit触发的事件名必须为input,所以有时会有冲突; 父组件: 子组件: (2)V3中:限制了popos接收的属性名…...

React16源码: React中创建更新的方式及ReactDOM.render的源码实现
React当中创建更新的主要方式 ReactDOM.render || hydrate 这两个API都是我们要把整个应用第一次进行渲染到我们的页面上面能够展现出来我们整个应用的样子的一个过程这是初次渲染 setState 后续更新应用 forceUpdate 后续更新应用 replaceState 在后续被舍弃 关于 ReactDOM…...

CentOS 7 系列默认的网卡接口名称
CentOS 7 系列默认的网卡接口是随机的,如果要修改网卡名称以 eth 开头,有两种方式。 方法一:安装系统时 在安装界面移动光标到 Install Centos 7.按 TAB 键 在出现的代码的末尾添加:net.ifnames0 biosdevname0.按下回车开始安装即…...

多文件上传
HTML中实现多文件上传是通过用<input type"file">元素的multiple属性,以下简单描述多文件上传的步骤 HTML表单准备,使用<input type"file">元素,并为其添加multiple属性,以允许用户选择多个文件…...

2024.1.7力扣每日一题——赎金信
2024.1.7 题目来源我的题解方法一 哈希表方法二 数组 题目来源 力扣每日一题;题序:383 我的题解 方法一 哈希表 使用哈希表记录ransomNote中所需字符的数量,然后遍历magazine并将哈希表中存在的对应的数量减一 时间复杂度:O(nm…...

C#中List<T>底层原理剖析
C#中List底层原理剖析 1. 基础用法2. List的Capacity与Count:3.List的底层原理3.1. 构造3.2 Add()接口3.3 Remove()接口3.4 Inster()接口3.5 Clear()接口3.6 Contains()接口3.7 ToArray()接口3.8 Find()接口3.8 Sort()接口 4. 总结5. 参考 1. 基础用法 list.Max() …...

Leetcode 3003. Maximize the Number of Partitions After Operations
Leetcode 3003. Maximize the Number of Partitions After Operations 1. 解题思路2. 代码实现 题目链接:10038. Maximize the Number of Partitions After Operations 1. 解题思路 这一题我看实际比赛当中只有72个人做出来,把我吓得够呛,…...
)
MySQL第一讲:MySQL知识体系详解(P6精通)
MySQL知识体系详解(P6精通) MySQL不论在实践还是面试中,都是频率最高的。本系列主要对MySQL知识体系梳理,将给大家构建JVM核心知识点全局知识体系,本文是MySQL第一讲,MySQL知识体系详解。 文章目录 MySQL知识体系详解(P6精通)1、MySQL学习建议1.1、为什么学习 MySQL?1.2、…...
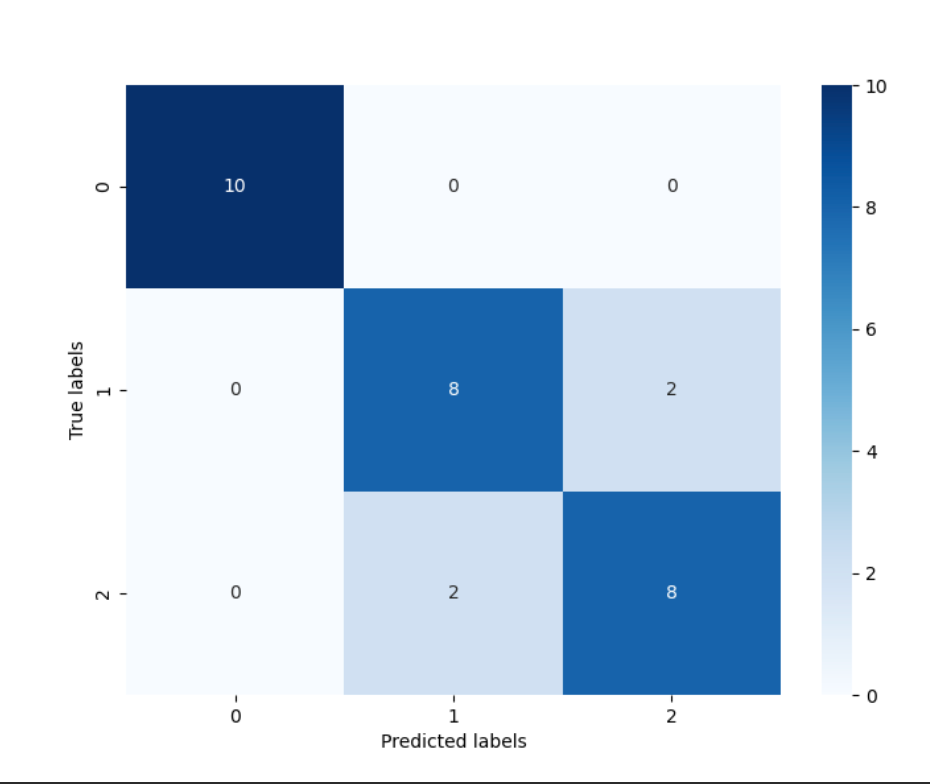
逻辑回归简单案例分析--鸢尾花数据集
文章目录 1. IRIS数据集介绍2. 具体步骤2.1 手动将数据转化为numpy矩阵2.1.1 从csv文件数据构建Numpy数据2.1.2 模型的搭建与训练2.1.3 分类器评估2.1.4 分类器的分类报告总结2.1.5 用交叉验证(Cross Validation)来验证分类器性能2.1.6 完整代码…...

Python print 高阶玩法
Python print 高阶玩法 当涉及到在Python中使用print函数时,有许多方式可以玩转文本样式、字体和颜色。在此将深入探讨这些主题,并介绍一些print函数的高级用法。 1. 基本的文本样式与颜色设置 使用ANSI转义码 ANSI转义码是一种用于在终端࿰…...
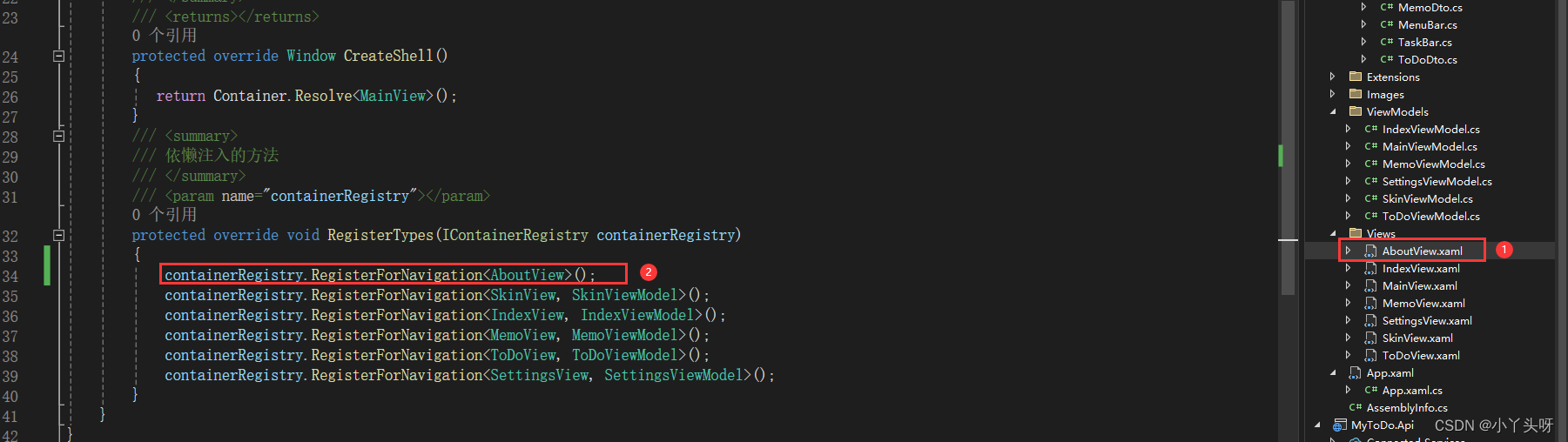
Wpf 使用 Prism 实战开发Day09
设置模块设计 1.效果图 一.系统设置模块,主要有个性化(用于更改主题颜色),系统设置,关于更多,3个功能点。 个性化的颜色内容样式,主要是从 Material Design Themes UI简称md、提供的demo里复制代码过来使用的。 1.设置…...
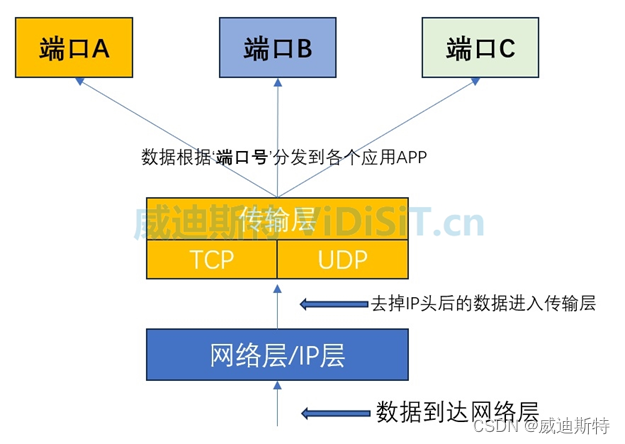
网络端口(包括TCP端口和UDP端口)的作用、定义、分类,以及在视频监控和流媒体通信中的定义
目 录 一、什么地方会用到网络端口? 二、端口的定义和作用 (一)TCP协议和UDP协议 (二)端口的定义 (三)在TCP/IP体系中,端口(TCP和UDP)的作用 (…...

【网络】每天掌握一个Linux命令 - iftop
在Linux系统中,iftop是网络管理的得力助手,能实时监控网络流量、连接情况等,帮助排查网络异常。接下来从多方面详细介绍它。 目录 【网络】每天掌握一个Linux命令 - iftop工具概述安装方式核心功能基础用法进阶操作实战案例面试题场景生产场景…...

HTML 列表、表格、表单
1 列表标签 作用:布局内容排列整齐的区域 列表分类:无序列表、有序列表、定义列表。 例如: 1.1 无序列表 标签:ul 嵌套 li,ul是无序列表,li是列表条目。 注意事项: ul 标签里面只能包裹 li…...

django filter 统计数量 按属性去重
在Django中,如果你想要根据某个属性对查询集进行去重并统计数量,你可以使用values()方法配合annotate()方法来实现。这里有两种常见的方法来完成这个需求: 方法1:使用annotate()和Count 假设你有一个模型Item,并且你想…...

基于当前项目通过npm包形式暴露公共组件
1.package.sjon文件配置 其中xh-flowable就是暴露出去的npm包名 2.创建tpyes文件夹,并新增内容 3.创建package文件夹...

【2025年】解决Burpsuite抓不到https包的问题
环境:windows11 burpsuite:2025.5 在抓取https网站时,burpsuite抓取不到https数据包,只显示: 解决该问题只需如下三个步骤: 1、浏览器中访问 http://burp 2、下载 CA certificate 证书 3、在设置--隐私与安全--…...

04-初识css
一、css样式引入 1.1.内部样式 <div style"width: 100px;"></div>1.2.外部样式 1.2.1.外部样式1 <style>.aa {width: 100px;} </style> <div class"aa"></div>1.2.2.外部样式2 <!-- rel内表面引入的是style样…...

三体问题详解
从物理学角度,三体问题之所以不稳定,是因为三个天体在万有引力作用下相互作用,形成一个非线性耦合系统。我们可以从牛顿经典力学出发,列出具体的运动方程,并说明为何这个系统本质上是混沌的,无法得到一般解…...

ardupilot 开发环境eclipse 中import 缺少C++
目录 文章目录 目录摘要1.修复过程摘要 本节主要解决ardupilot 开发环境eclipse 中import 缺少C++,无法导入ardupilot代码,会引起查看不方便的问题。如下图所示 1.修复过程 0.安装ubuntu 软件中自带的eclipse 1.打开eclipse—Help—install new software 2.在 Work with中…...

RNN避坑指南:从数学推导到LSTM/GRU工业级部署实战流程
本文较长,建议点赞收藏,以免遗失。更多AI大模型应用开发学习视频及资料,尽在聚客AI学院。 本文全面剖析RNN核心原理,深入讲解梯度消失/爆炸问题,并通过LSTM/GRU结构实现解决方案,提供时间序列预测和文本生成…...

优选算法第十二讲:队列 + 宽搜 优先级队列
优选算法第十二讲:队列 宽搜 && 优先级队列 1.N叉树的层序遍历2.二叉树的锯齿型层序遍历3.二叉树最大宽度4.在每个树行中找最大值5.优先级队列 -- 最后一块石头的重量6.数据流中的第K大元素7.前K个高频单词8.数据流的中位数 1.N叉树的层序遍历 2.二叉树的锯…...
