7.27 SpringBoot项目实战 之 整合Swagger
相关文章：
7.27 SpringBoot项目实战 之 整合Swagger
文章目录 前言一、Maven依赖二、编写Swagger配置类三、编写接口配置3.1 控制器Controller 配置描述3.2 接口API 配置描述3.3 参数配置描述3.4 忽略API四、全局参数配置五、启用增强功能六、调试前言 在我们实现了那么多API以后，进入前后端联调阶段，需要给前端同学提供接口文…...
创建第一个SpringMVC项目，入手必看！
文章目录 创建第一个SpringMVC项目，入手必看！1、新建一个maven空项目，在pom.xml中设置打包为war之前，右击项目添加web框架2、如果点击右键没有添加框架或者右击进去后没有web框架，点击左上角file然后进入项目结构在模块…...
go 切片长度与容量的区别
切片的声明 切片可以看成是数组的引用（实际上切片的底层数据结构确实是数组）。在 Go 中，每个数组的大小是固定的，不能随意改变大小，切片可以为数组提供动态增长和缩小的需求，但其本身并不存储任何数据。 …...
回归和分类区别
回归任务（Regression）： 特点： 输出是连续值，通常是实数。任务目标是预测或估计一个数值。典型应用包括房价预测、销售额预测、温度预测等。 目标： 最小化预测值与真实值之间的差异，通常使用…...
docker nginx滚动日志配置
将所有日志打印到控制台 nginx.conf user nginx; worker_processes auto; # 日志打印控制台 error_log /dev/stdout; #error_log /var/log/nginx/error.log notice; pid /var/run/nginx.pid;events {worker_connections 1024; }http {include /etc/nginx/m…...
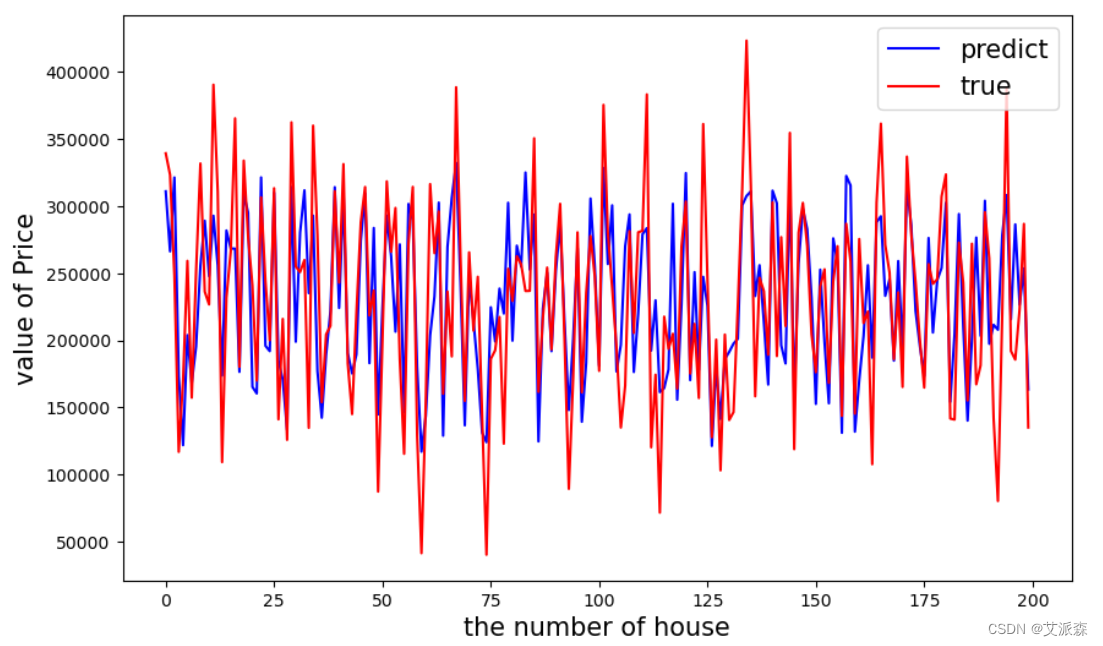
大数据分析案例-基于LinearRegression回归算法构建房屋价格预测模型
🤵♂️ 个人主页：艾派森的个人主页 ✍🏻作者简介：Python学习者 🐋 希望大家多多支持，我们一起进步！😄 如果文章对你有帮助的话， 欢迎评论 💬点赞Ǵ…...
React-hook-form-mui（一）：基本使用
前言 在项目开发中，我们选择了ReactMUI作为技术栈。在使用MUI构建form表单时，我们发现并没有与antd类似的表单验证功能，于是我们选择了MUI推荐使用的react-hook-form-mui库去进行验证。但是发现网上关于这个库的使用方法和demo比较少且比较简…...
python总结-生成器与迭代器
生成器与迭代器 生成器生成器定义为什么要有生成器创建生成器的方式一(生成器表达式) 创建生成器的方式二(生成器函数)生成器函数的工作原理总结 迭代器概念可迭代对象和迭代器区别for循环的本质创建一个迭代器 动态添加属性和方法运行过程中给对象、类添加属性和方法types.Met…...
MySQL如何从数据中截取所需要的字符串
MySQL如何从数据中截取所需要的字符串 背景 有这样的一个场景,我想从我的表里面进行数据截取，我的数据内容大致如下： 张三-建外SOHO-2-16 POA 20210518.pdf 我想获取数据中的：20210518这一日期部分，需要如何实现？ 解…...
动态加载和动态链接的区别
动态加载（Dynamic Loading）和动态链接（Dynamic Linking）是两个与程序运行时加载和使用代码相关的概念，它们有一些区别： 动态加载（Dynamic Loading）： 定义： 动…...
js数组循环,当前循环完成后执行下次循环
前言 上图中，点击播放icon，图中左边地球视角会按照视角列表依次执行。u3D提供了api,但是我们如何保证在循环中依次执行。即第一次执行完成后，再走第二次循环。很多人的第一思路就是promise。对，不错，出发的思路是正确的…...
决策树（Decision Trees）
决策树（Decision Trees）是一种基于树形结构进行决策的模型，广泛应用于分类和回归任务。它通过对数据集进行递归划分，构建一棵树，每个节点代表一个特征，每个分支代表一个决策规则，叶节点存储一个…...
湖南大学-计算机网路-2023期末考试【部分原题回忆】
前言 计算机网络第一门考，而且没考好，回忆起来的原题不多。 这门学科学的最认真，复习的最久，考的最差。 教材使用这本书： 简答题（6*530分） MTU和MSS分别是什么，联系是什么&#x…...
LCD—液晶显示
本节主要介绍以下内容 显示器简介 液晶控制原理 秉火3.2寸液晶屏简介 使用FSMC模拟8080时序 NOR FLASH时序结构体 FSMC初始化结构体 一、显示器简介 显示器属于计算机的I/O设备，即输入输出设备。它是一种将特定电子信息输出到屏幕上再反射到人眼的显示工具。…...
论正确初始化深度学习模型参数的重要性
遇到的问题：在一般的深度学习训练过程中，我们建立好模型以后，程序就有自动的初始化一些模型的参数，比如全连接层中每一个节点的权重等等，在之前的网络训练过程中，我总是事先设下随机种子以后，让…...
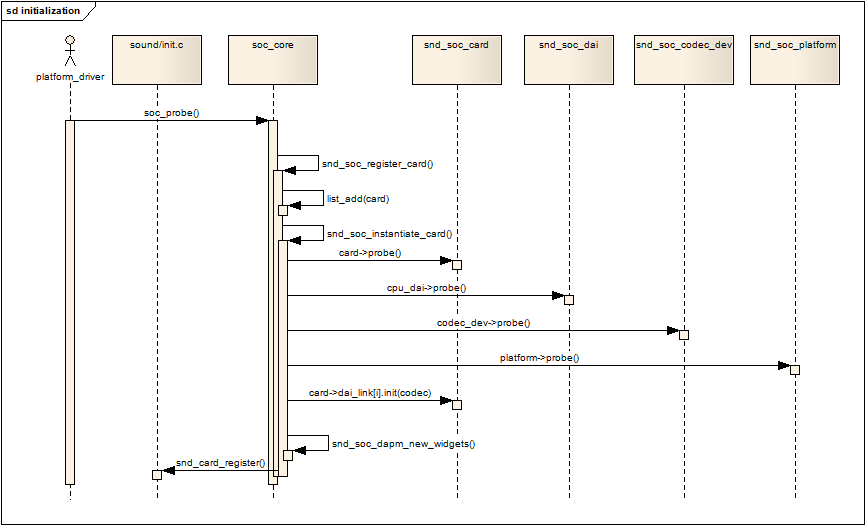
ALSA学习(5)——ASoC架构中的Machine
参考博客：https://blog.csdn.net/DroidPhone/article/details/7231605 （以下内容皆为原博客转载） 文章目录 一、注册Platform Device二、注册Platform Driver三、初始化入口soc_probe() 一、注册Platform Device ASoC把声卡注册为Platform …...
LeetCode 0447.回旋镖的数量：哈希表
【LetMeFly】447.回旋镖的数量：哈希表 力扣题目链接：https://leetcode.cn/problems/number-of-boomerangs/ 给定平面上 n 对 互不相同 的点 points ，其中 points[i] [xi, yi] 。回旋镖 是由点 (i, j, k) 表示的元组 ，其中 i 和…...
容器相关笔记
目录 1.容器 1.什么是容器 2.java中的容器 3.容器里存放的是引用数据类型（存对象的地址，不是对象本身），不能存基本数据类型 4.容器存放的两种格式 5.容器类所在的包 6.容器的分类 1.Collection，存放单一的类型 1.List&…...
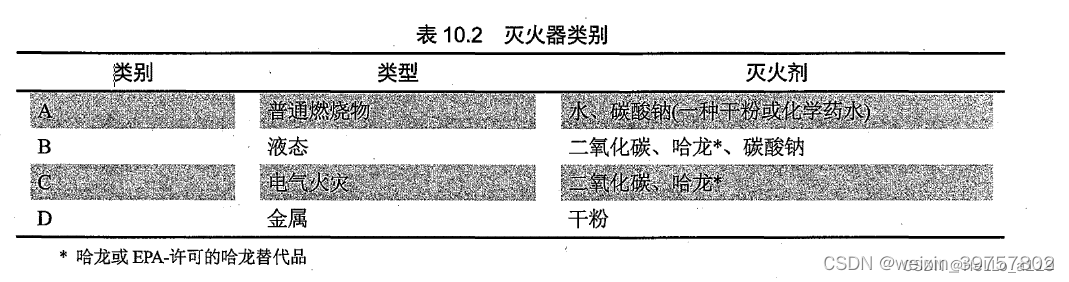
cissp 第10章 : 物理安全要求
10.1 站点与设施设计的安全原则 物理控制是安全防护的第一条防线，而人员是最后一道防线。 10.1.1 安全设施计划 安全设施计划描述了组织的安全要求的轮廓， 并且着重强调为了提供安全性所用的方法和机制。 这样的计划通过被称为关键路径分析的过程进行开…...
聊一聊 .NET高级调试 内核模式堆泄露
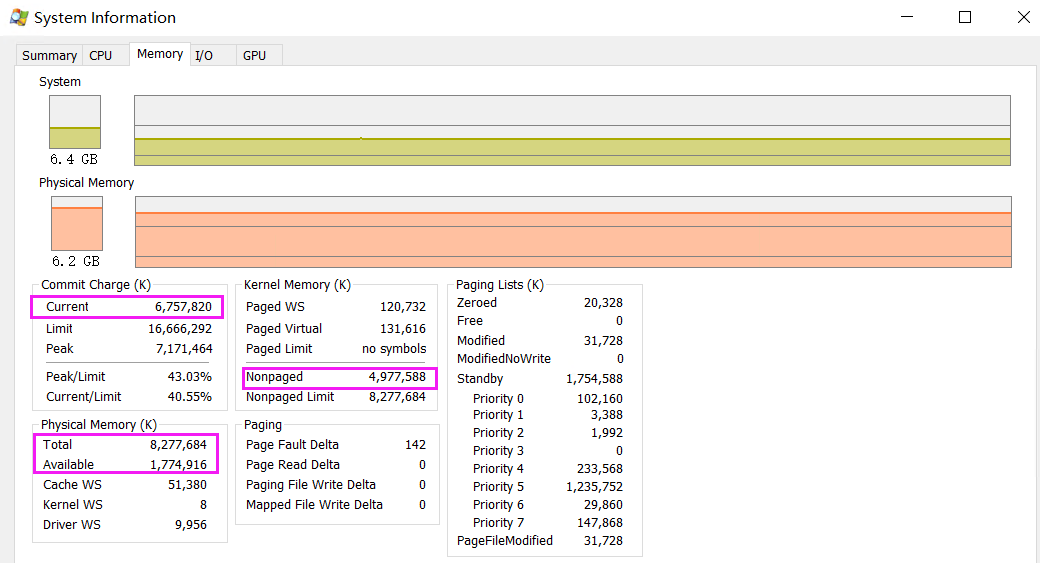
一：背景 1. 讲故事 前几天有位朋友找到我，说他的机器内存在不断的上涨，但在任务管理器中查不出是哪个进程吃的内存，特别奇怪，截图如下： 在我的分析旅程中都是用户态模式的内存泄漏，像上图中的…...
超短脉冲激光自聚焦效应
前言与目录 强激光引起自聚焦效应机理 超短脉冲激光在脆性材料内部加工时引起的自聚焦效应，这是一种非线性光学现象，主要涉及光学克尔效应和材料的非线性光学特性。 自聚焦效应可以产生局部的强光场，对材料产生非线性响应，可能…...
JavaScript 中的 ES|QL：利用 Apache Arrow 工具
作者：来自 Elastic Jeffrey Rengifo 学习如何将 ES|QL 与 JavaScript 的 Apache Arrow 客户端工具一起使用。 想获得 Elastic 认证吗？了解下一期 Elasticsearch Engineer 培训的时间吧！ Elasticsearch 拥有众多新功能，助你为自己…...
【机器视觉】单目测距——运动结构恢复
ps：图是随便找的，为了凑个封面 前言 在前面对光流法进行进一步改进，希望将2D光流推广至3D场景流时，发现2D转3D过程中存在尺度歧义问题，需要补全摄像头拍摄图像中缺失的深度信息，否则解空间不收敛…...
Keil 中设置 STM32 Flash 和 RAM 地址详解
文章目录 Keil 中设置 STM32 Flash 和 RAM 地址详解一、Flash 和 RAM 配置界面（Target 选项卡）1. IROM1（用于配置 Flash）2. IRAM1（用于配置 RAM）二、链接器设置界面（Linker 选项卡）1. 勾选“Use Memory Layout from Target Dialog”2. 查看链接器参数（如果没有勾选上面…...
CocosCreator 之 JavaScript/TypeScript和Java的相互交互
引擎版本： 3.8.1 语言： JavaScript/TypeScript、C、Java 环境：Window 参考：Java原生反射机制 您好，我是鹤九日！ 回顾 在上篇文章中：CocosCreator Android项目接入UnityAds 广告SDK。 我们简单讲…...
Spring AI 入门：Java 开发者的生成式 AI 实践之路
一、Spring AI 简介 在人工智能技术快速迭代的今天，Spring AI 作为 Spring 生态系统的新生力量，正在成为 Java 开发者拥抱生成式 AI 的最佳选择。该框架通过模块化设计实现了与主流 AI 服务（如 OpenAI、Anthropic）的无缝对接&…...
【RockeMQ】第2节｜RocketMQ快速实战以及核⼼概念详解（二）
升级Dledger高可用集群 一、主从架构的不足与Dledger的定位 主从架构缺陷 数据备份依赖Slave节点，但无自动故障转移能力，Master宕机后需人工切换，期间消息可能无法读取。Slave仅存储数据，无法主动升级为Master响应请求ÿ…...
C++使用 new 来创建动态数组
问题： 不能使用变量定义数组大小 原因： 这是因为数组在内存中是连续存储的，编译器需要在编译阶段就确定数组的大小，以便正确地分配内存空间。如果允许使用变量来定义数组的大小，那么编译器就无法在编译时确定数组的大…...
HarmonyOS运动开发：如何用mpchart绘制运动配速图表
##鸿蒙核心技术##运动开发##Sensor Service Kit（传感器服务）# 前言 在运动类应用中，运动数据的可视化是提升用户体验的重要环节。通过直观的图表展示运动过程中的关键数据，如配速、距离、卡路里消耗等，用户可以更清晰…...
Chromium 136 编译指南 Windows篇：depot_tools 配置与源码获取（二）
引言 工欲善其事，必先利其器。在完成了 Visual Studio 2022 和 Windows SDK 的安装后，我们即将接触到 Chromium 开发生态中最核心的工具——depot_tools。这个由 Google 精心打造的工具集，就像是连接开发者与 Chromium 庞大代码库的智能桥梁…...