OCS2 入门教程(四)- 机器人示例
系列文章目录
前言
OCS2 包含多个机器人示例。我们在此简要讨论每个示例的主要特点。
| System | State Dim. | Input Dim. | Constrained | Caching |
|---|---|---|---|---|
| Double Integrator | 2 | 1 | No | No |
| Cartpole | 4 | 1 | Yes | No |
| Ballbot | 10 | 3 | No | No |
| Quadrotor | 12 | 4 | No | No |
| Mobile Manipulator | 6-13 | 6-13 | Yes | Yes / No |
| Legged Robot | 24 | 24 | Yes | No |
对于所有这些机器人示例,有两个独立的软件包:
- ocs2_<robot>: 提供机器人专用 MPC 实现库。
- ocs2_<robot>_ros: 用 ROS 封装 MPC 实现,以定义 ROS 节点。
一、Double Integrator
双积分器示例是我们最简单的问题。它模拟了一个沿 x 方向移动的一维点质量。模型是线性的,成本函数是二次函数。目标点通过参考管理器模块设置为二次成本。
# Build the example
catkin build ocs2_double_integrator_ros
# Source workspace
# Do not forget to change <...> parts
source <directory_to_ws>/<catkin_ws_name>/devel/setup.bash# Launch the example
roslaunch ocs2_double_integrator_ros double_integrator.launch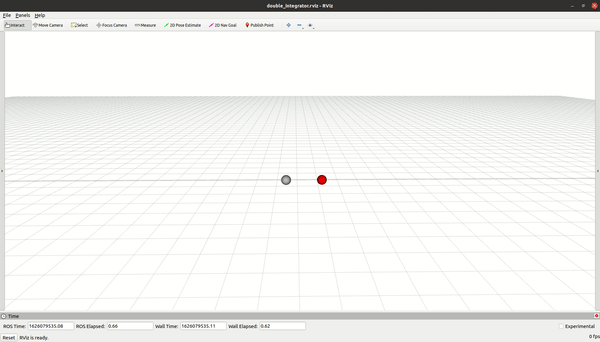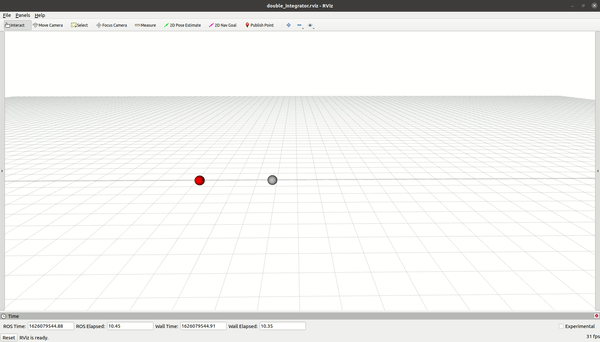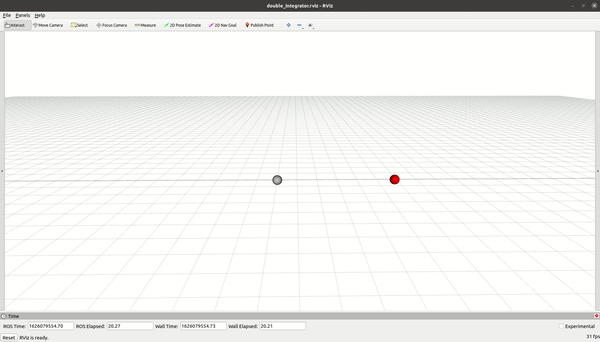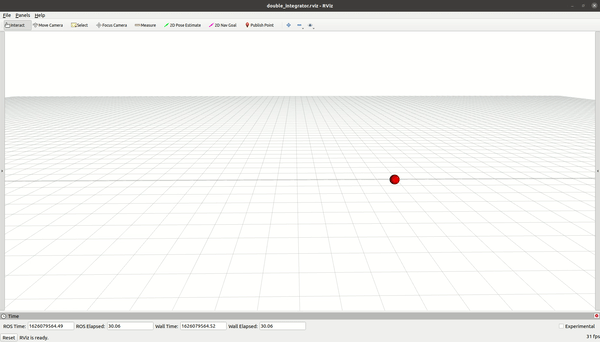
二、Cartpole
推车杆的例子是一个典型的控制问题,一根杆子通过一个无驱动的接头连接到一辆小车上。小车沿着无摩擦轨道移动。目标是在遵守输入限制的前提下,通过沿轨道加速或减速小车,使摆锤从右下方位置开始摆动起来并保持平衡。
# Build the example
catkin build ocs2_cartpole_ros
# Source workspace
# Do not forget to change <...> parts
source <directory_to_ws>/<catkin_ws_name>/devel/setup.bash# Launch the example
roslaunch ocs2_cartpole_ros cartpole.launch
三、Ballbot
Ballbot 是一个 5DoF 系统。该平台是一个扭矩控制的全向机器人,通过三个全向轮在一个球上保持平衡。该系统具有非线性动力学特性,并表现出非最小相位行为。系统动力学以 Ballbot 的前向动力学为基础,通过自动微分计算流量图的线性近似值。任务目标是根据用户指令控制机器人的 XY 位置和偏航。
# Build the example
catkin build ocs2_ballbot_ros
# Source workspace
# Do not forget to change <...> parts
source <directory_to_ws>/<catkin_ws_name>/devel/setup.bash# Launch the example
roslaunch ocs2_ballbot_ros ballbot.launch
四、Quadrotor
四旋翼机器人示例是一个 6DoF 系统。平台建模为浮动基座、刚体动力学、三维力矩和机器人法线方向的一维力控制。系统动力学及其导数均由代码生成。本示例旨在跟踪用户指令,该指令定义为四旋翼机器人的三维位置和偏航。
# Build the example
catkin build ocs2_quadrotor_ros
# Source workspace
# Do not forget to change <...> parts
source <directory_to_ws>/<catkin_ws_name>/devel/setup.bash# Launch the example
roslaunch ocs2_quadrotor_ros quadrotor.launch
五、Mobile Manipulator
移动机械手示例是一个全运动学问题。模型包括一个 6DOF 机械臂和移动底座的 2D 位置和航向。控制输入为机械臂的 6 个关节速度以及底座的前进速度和旋转速度。任务目标是跟踪 6DoF 末端执行器姿势。关节位置和速度限制包含在最优控制问题的约束条件中。避免自碰撞是根据 URDF 模型中的碰撞体和避免碰撞约束来实现的(参见 ocs2_self_collision)。
注:本例实现了 MPC 的缓存和非缓存变体,可通过配置文件中的 usePreComputation 标志进行选择。
系统模型通过解析 URDF 和任务文件确定。目前支持以下系统模型:
- 默认(值:0): 通过解析 URDF 获得的默认系统模型。
- 驱动假轮距(值:1): 在从 URDF 解析的模型中添加一个假 XY-Yaw 关节,该关节在整体动力学约束(速度控制)下被驱动。这是一个由 SE(2) 控制底座的移动机械手模型。
- Unactuated 假浮动基座(值:2): 在从 URDF 解析出的模型中添加一个未驱动的 XYZ-RPY 假关节。
- 激活的虚拟浮动基点(值:3): 为从 URDF 中解析出的模型添加一个完全致动(速度控制)的 XYZ-RPY 假关节。这是一个用 SE(3) 控制基座的移动机械手模型。
要玩转不同的模型类型,可以更改 task.info 文件中的模型信息。
# Build the example
catkin build ocs2_mobile_manipulator_ros
# Source workspace
# Do not forget to change <...> parts
source <directory_to_ws>/<catkin_ws_name>/devel/setup.bash对于几种常见的机器人机械手,我们提供了使用 OCS2 运行它们的示例。这里提供了生成机器人模型文件(URDF)的步骤。
在其中一些示例中,我们通过 task.info 文件中的 model_information.removeJoints 属性固定了 URDF 中的某些关节(如抓手手指关节或车轮关节)。这样就可以简化所构建的 Pinocchio 模型。仅出于 rviz 可视化目的,task.info 文件中 removeJoints 属性下的关节将通过虚拟仿真节点发布在零关节位置。
警告
对于这些示例,可能需要对 MPC 进行额外调整才能在硬件上运行。此外,对于某些示例,需要将碰撞网格简化为原始形状(如圆柱和方框),以便避免碰撞。
我们欢迎社会各界为这些用例做出贡献。
5.1 Mabi-Mobile
roslaunch ocs2_mobile_manipulator_ros manipulator_mabi_mobile.launch
5.2 Kinova Jaco2
# For 6-Dof
roslaunch ocs2_mobile_manipulator_ros manipulator_kinova_j2n6.launch
# For 7-Dof
roslaunch ocs2_mobile_manipulator_ros manipulator_kinova_j2n7.launch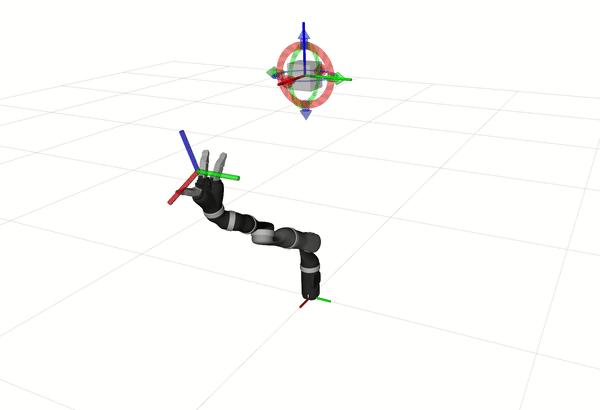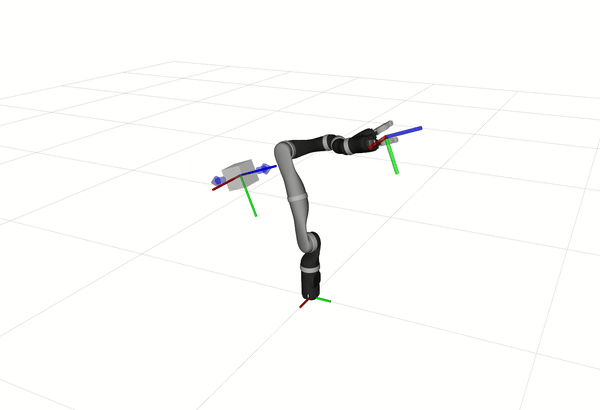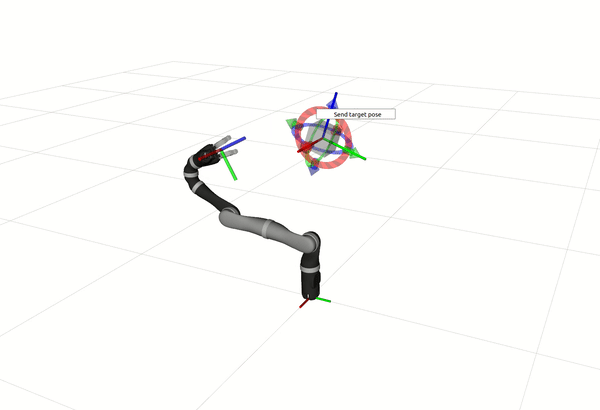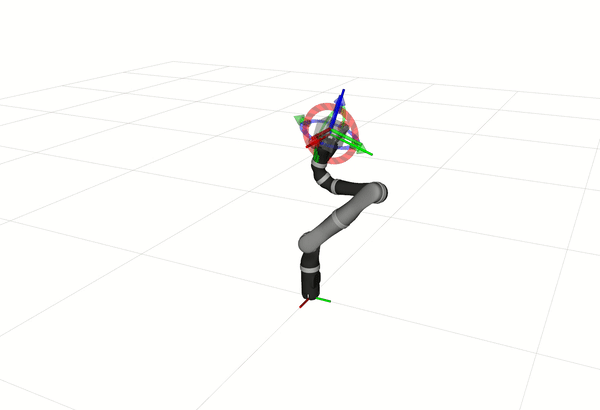
5.3 Franka Panda
roslaunch ocs2_mobile_manipulator_ros manipulator_franka.launch
5.4 Willow Garage PR2
roslaunch ocs2_mobile_manipulator_ros manipulator_pr2.launch
5.5 Clearpath Ridgeback with UR-5
roslaunch ocs2_mobile_manipulator_ros manipulator_ridgeback_ur5.launch 
六、Legged Robot
腿部机器人示例是一个开关系统问题。它采用 MPC 方法对四足机器人 Anymal 进行运动控制。机器人的步态由用户定义,并可在执行过程中通过解算器同步模块(步态接收器)进行修改。模式序列和目标轨迹通过参考管理器模块(SwitchedModelReferenceManager)进行定义。成本函数为二次罚则,用于跟踪指令的基座位置和偏航,并将机器人的重量平均分配到站立脚上。该问题有几个取决于模式的约束条件,例如摆动脚的力为零,站立脚的速度为零。在接触力上强制执行摩擦锥,为避免脚擦伤,摆动脚在 Z 方向上跟踪预定义的运动。
系统动力学有两种建模方式,可从配置文件中选择:
- 单刚体动力学(SRBD): 该模型假定系统具有恒定惯性,与关节位置无关。
- 全中心动力学(FCD): 该模型使用中心动力学,包含机器人四肢的运动。与 SRBD 相似,它考虑了机器人的全运动学。
# Build the example
catkin build ocs2_legged_robot_ros
# Source workspace
# Do not forget to change <...> parts
source <directory_to_ws>/<catkin_ws_name>/devel/setup.bash# Launch the example for DDP
roslaunch ocs2_legged_robot_ros legged_robot_ddp.launch
# OR launch the example for SQP
roslaunch ocs2_legged_robot_ros legged_robot_sqp.launch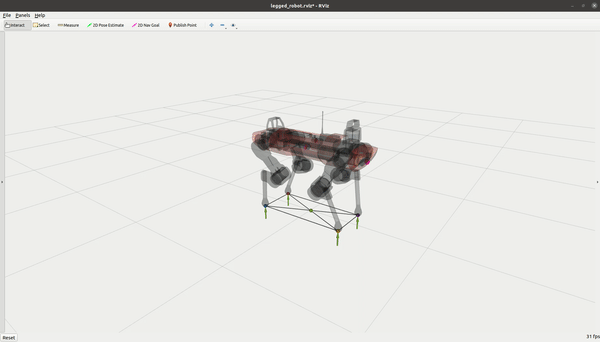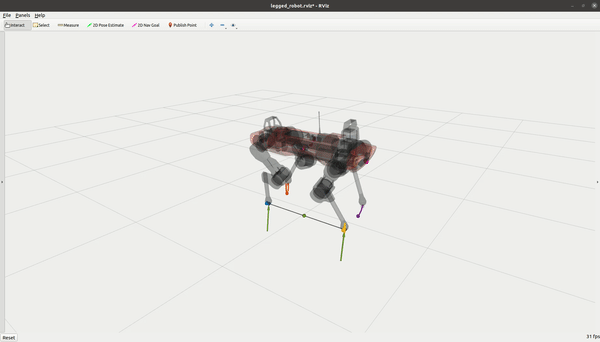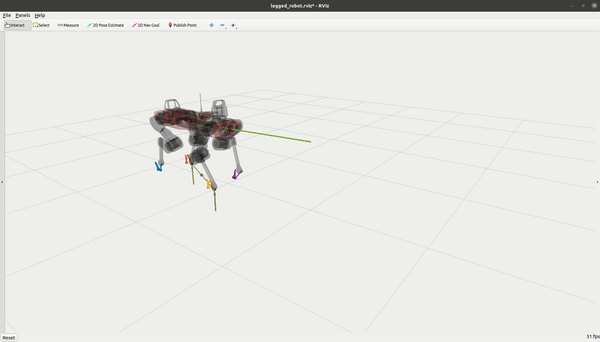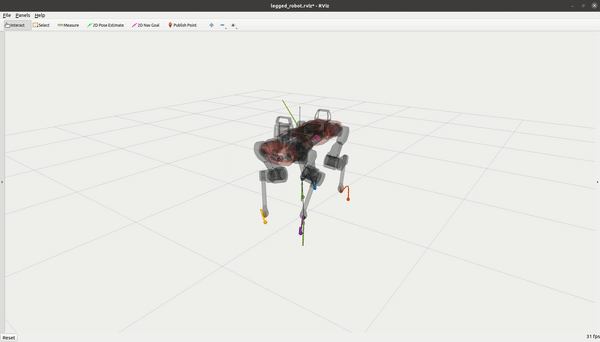
相关文章:

OCS2 入门教程(四)- 机器人示例
系列文章目录 前言 OCS2 包含多个机器人示例。我们在此简要讨论每个示例的主要特点。 System State Dim. Input Dim. Constrained Caching Double Integrator 2 1 No No Cartpole 4 1 Yes No Ballbot 10 3 No No Quadrotor 12 4 No No Mobile Manipul…...

FreeRTOS学习第6篇–任务状态挂起恢复删除等操作
目录 FreeRTOS学习第6篇--任务状态挂起恢复删除等操作任务的状态设计实验IRReceiver_Task任务相关代码片段实验现象本文中使用的测试工程 FreeRTOS学习第6篇–任务状态挂起恢复删除等操作 本文目标:学习与使用FreeRTOS中的几项操作,有挂起恢复删除等操作…...
BLE Mesh蓝牙组网技术详细解析之Access Layer访问层(六)
目录 一、什么是BLE Mesh Access Layer访问层? 二、Access payload 2.1 Opcode 三、Access layer behavior 3.1 Access layer发送消息的流程 3.2 Access layer接收消息的流程 3.3 Unacknowledged and acknowledged messages 3.3.1 Unacknowledged message …...

Netlink 通信机制
文章目录 前言一、Netlink 介绍二、示例代码参考资料 前言 一、Netlink 介绍 Netlink套接字是用以实现用户进程与内核进程通信的一种特殊的进程间通信(IPC) ,也是网络应用程序与内核通信的最常用的接口。 在Linux 内核中,使用netlink 进行应用与内核通信的应用有…...

2024.1.8每日一题
LeetCode 回旋镖的数量 447. 回旋镖的数量 - 力扣(LeetCode) 题目描述 给定平面上 n 对 互不相同 的点 points ,其中 points[i] [xi, yi] 。回旋镖 是由点 (i, j, k) 表示的元组 ,其中 i 和 j 之间的距离和 i 和 k 之间的欧式…...
看了致远OA的表单设计后的思考
更多ruoyi-nbcio功能请看演示系统 gitee源代码地址 前后端代码: https://gitee.com/nbacheng/ruoyi-nbcio 演示地址:RuoYi-Nbcio后台管理系统 更多nbcio-boot功能请看演示系统 gitee源代码地址 后端代码: https://gitee.com/nbacheng/n…...
mmdetection训练自己的数据集
mmdetection训练自己的数据集 这里写目录标题 mmdetection训练自己的数据集一: 环境搭建二:数据集格式转换(yolo转coco格式)yolo数据集格式coco数据集格式yolo转coco数据集格式yolo转coco数据集格式的代码 三: 训练dataset数据文件配置config…...

MySQL取出N列里最大or最小的一个数据
如题,现在有3列,都是数字类型,要取出这3列里最大或最小的的一个数字 -- N列取最小 SELECT LEAST(temperature_a,temperature_b,temperature_c) min FROM infrared_heat-- N列取最大 SELECT GREATEST(temperature_a,temperature_b,temperat…...
编写.NET的Dockerfile文件构建镜像
创建一个WebApi项目,并且创建一个Dockerfile空文件,添加以下代码,7.0代表的你项目使用的SDK的版本,构建的时候也需要选择好指定的镜像tag FROM mcr.microsoft.com/dotnet/aspnet:7.0 AS base WORKDIR /app EXPOSE 80 EXPOSE 443F…...
 练习7-4 找出不是两个数组共有的元素)
【C语言】浙大版C语言程序设计(第三版) 练习7-4 找出不是两个数组共有的元素
前言 最近在学习浙大版的《C语言程序设计》(第三版)教材,同步在PTA平台上做对应的练习题。这道练习题花了比较长的时间,于是就写篇博文记录一下我的算法和代码。 2024.01.03 题目 练习7-4 找出不是两个数组共有的元素 作者 张彤…...

7.27 SpringBoot项目实战 之 整合Swagger
文章目录 前言一、Maven依赖二、编写Swagger配置类三、编写接口配置3.1 控制器Controller 配置描述3.2 接口API 配置描述3.3 参数配置描述3.4 忽略API四、全局参数配置五、启用增强功能六、调试前言 在我们实现了那么多API以后,进入前后端联调阶段,需要给前端同学提供接口文…...
创建第一个SpringMVC项目,入手必看!
文章目录 创建第一个SpringMVC项目,入手必看!1、新建一个maven空项目,在pom.xml中设置打包为war之前,右击项目添加web框架2、如果点击右键没有添加框架或者右击进去后没有web框架,点击左上角file然后进入项目结构在模块…...

go 切片长度与容量的区别
切片的声明 切片可以看成是数组的引用(实际上切片的底层数据结构确实是数组)。在 Go 中,每个数组的大小是固定的,不能随意改变大小,切片可以为数组提供动态增长和缩小的需求,但其本身并不存储任何数据。 …...

回归和分类区别
回归任务(Regression): 特点: 输出是连续值,通常是实数。任务目标是预测或估计一个数值。典型应用包括房价预测、销售额预测、温度预测等。 目标: 最小化预测值与真实值之间的差异,通常使用…...

docker nginx滚动日志配置
将所有日志打印到控制台 nginx.conf user nginx; worker_processes auto; # 日志打印控制台 error_log /dev/stdout; #error_log /var/log/nginx/error.log notice; pid /var/run/nginx.pid;events {worker_connections 1024; }http {include /etc/nginx/m…...
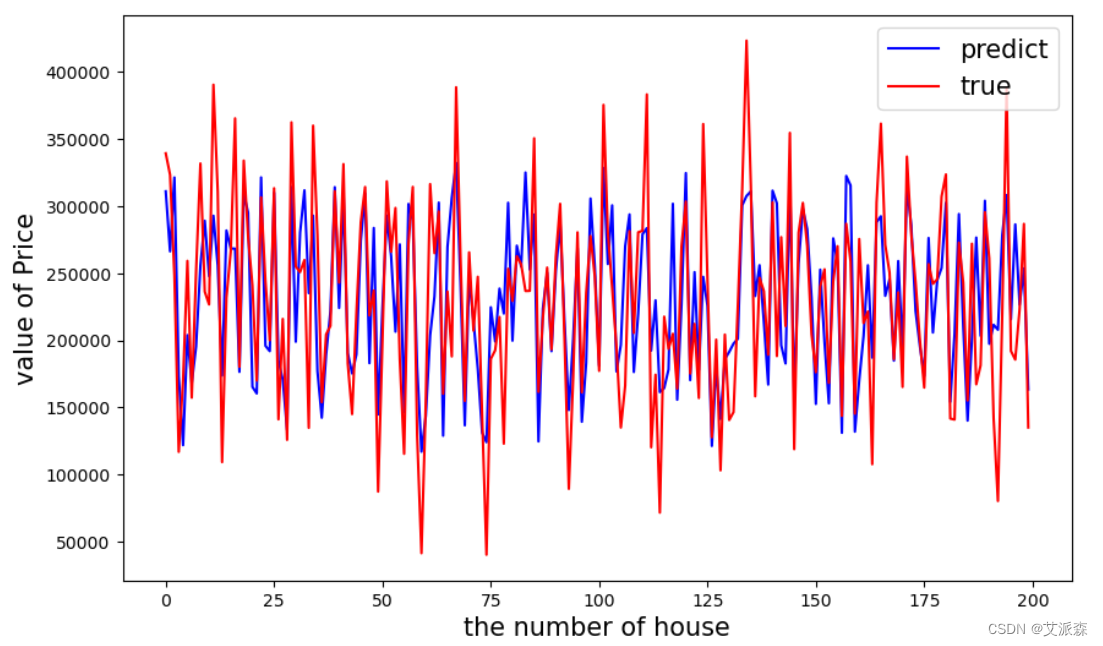
大数据分析案例-基于LinearRegression回归算法构建房屋价格预测模型
🤵♂️ 个人主页:艾派森的个人主页 ✍🏻作者简介:Python学习者 🐋 希望大家多多支持,我们一起进步!😄 如果文章对你有帮助的话, 欢迎评论 💬点赞Ǵ…...
:基本使用)
React-hook-form-mui(一):基本使用
前言 在项目开发中,我们选择了ReactMUI作为技术栈。在使用MUI构建form表单时,我们发现并没有与antd类似的表单验证功能,于是我们选择了MUI推荐使用的react-hook-form-mui库去进行验证。但是发现网上关于这个库的使用方法和demo比较少且比较简…...

python总结-生成器与迭代器
生成器与迭代器 生成器生成器定义为什么要有生成器创建生成器的方式一(生成器表达式) 创建生成器的方式二(生成器函数)生成器函数的工作原理总结 迭代器概念可迭代对象和迭代器区别for循环的本质创建一个迭代器 动态添加属性和方法运行过程中给对象、类添加属性和方法types.Met…...

MySQL如何从数据中截取所需要的字符串
MySQL如何从数据中截取所需要的字符串 背景 有这样的一个场景,我想从我的表里面进行数据截取,我的数据内容大致如下: 张三-建外SOHO-2-16 POA 20210518.pdf 我想获取数据中的:20210518这一日期部分,需要如何实现? 解…...

动态加载和动态链接的区别
动态加载(Dynamic Loading)和动态链接(Dynamic Linking)是两个与程序运行时加载和使用代码相关的概念,它们有一些区别: 动态加载(Dynamic Loading): 定义: 动…...

XML Group端口详解
在XML数据映射过程中,经常需要对数据进行分组聚合操作。例如,当处理包含多个物料明细的XML文件时,可能需要将相同物料号的明细归为一组,或对相同物料号的数量进行求和计算。传统实现方式通常需要编写脚本代码,增加了开…...

web vue 项目 Docker化部署
Web 项目 Docker 化部署详细教程 目录 Web 项目 Docker 化部署概述Dockerfile 详解 构建阶段生产阶段 构建和运行 Docker 镜像 1. Web 项目 Docker 化部署概述 Docker 化部署的主要步骤分为以下几个阶段: 构建阶段(Build Stage):…...

Android Wi-Fi 连接失败日志分析
1. Android wifi 关键日志总结 (1) Wi-Fi 断开 (CTRL-EVENT-DISCONNECTED reason3) 日志相关部分: 06-05 10:48:40.987 943 943 I wpa_supplicant: wlan0: CTRL-EVENT-DISCONNECTED bssid44:9b:c1:57:a8:90 reason3 locally_generated1解析: CTR…...

k8s从入门到放弃之Ingress七层负载
k8s从入门到放弃之Ingress七层负载 在Kubernetes(简称K8s)中,Ingress是一个API对象,它允许你定义如何从集群外部访问集群内部的服务。Ingress可以提供负载均衡、SSL终结和基于名称的虚拟主机等功能。通过Ingress,你可…...

STM32F4基本定时器使用和原理详解
STM32F4基本定时器使用和原理详解 前言如何确定定时器挂载在哪条时钟线上配置及使用方法参数配置PrescalerCounter ModeCounter Periodauto-reload preloadTrigger Event Selection 中断配置生成的代码及使用方法初始化代码基本定时器触发DCA或者ADC的代码讲解中断代码定时启动…...

OkHttp 中实现断点续传 demo
在 OkHttp 中实现断点续传主要通过以下步骤完成,核心是利用 HTTP 协议的 Range 请求头指定下载范围: 实现原理 Range 请求头:向服务器请求文件的特定字节范围(如 Range: bytes1024-) 本地文件记录:保存已…...

基于Docker Compose部署Java微服务项目
一. 创建根项目 根项目(父项目)主要用于依赖管理 一些需要注意的点: 打包方式需要为 pom<modules>里需要注册子模块不要引入maven的打包插件,否则打包时会出问题 <?xml version"1.0" encoding"UTF-8…...

MySQL中【正则表达式】用法
MySQL 中正则表达式通过 REGEXP 或 RLIKE 操作符实现(两者等价),用于在 WHERE 子句中进行复杂的字符串模式匹配。以下是核心用法和示例: 一、基础语法 SELECT column_name FROM table_name WHERE column_name REGEXP pattern; …...

python执行测试用例,allure报乱码且未成功生成报告
allure执行测试用例时显示乱码:‘allure’ �����ڲ����ⲿ���Ҳ���ǿ�&am…...

ABAP设计模式之---“简单设计原则(Simple Design)”
“Simple Design”(简单设计)是软件开发中的一个重要理念,倡导以最简单的方式实现软件功能,以确保代码清晰易懂、易维护,并在项目需求变化时能够快速适应。 其核心目标是避免复杂和过度设计,遵循“让事情保…...
