PCA主成分分析算法
在数据分析中,如果特征太多,或者特征之间的相关性太高,通常可以用PCA来进行降维。比如通过对原有10个特征的线性组合, 我们找出3个主成分,就足以解释绝大多数的方差,该算法在高维数据集中被广泛应用。
算法(没时间看版本):
- 将数据标准化,即把所有数据转换以原点为中心;
- 划一条通过原点的直线,将所有点投影到该直线上,然后计算这些投影点到原点的距离平方和。设想我们不停的转动该直线,最终找到一条直线使得这个距离平方和最大,也就是该直线最接近所有的点,该直线为特征向量的方向,称为PC1,这个距离平方和即为特征值;
- 按同样的方法,找到第二条直线,该直线与PC1垂直且距离平方和最大,为PC2;
- 重复该过程直到找到所有的PC;
- 根据需求,确定头部的几个PC可以解释绝大多数方差。
下面先给出几个相关的概念。
协方差和散度矩阵
样本均值:
x ˉ = 1 n ∑ i = 1 N x i \bar{x} = \frac{1}{n} \sum_{i=1}^N x_i xˉ=n1i=1∑Nxi
样本方差:
S 2 = 1 n − 1 ∑ i = 1 n ( x i − x ˉ ) 2 S^2=\frac{1}{n-1} \sum_{i=1}^n {(x_i-\bar{x})}^2 S2=n−11i=1∑n(xi−xˉ)2
样本X和样本Y的协方差:
C o v ( X , Y ) = E [ ( X − E ( X ) ) ( Y − E ( Y ) ) ] = 1 n − 1 ∑ i = 1 n ( x i − x ˉ ) ( y i − y ˉ ) Cov(X,Y)=E[(X-E(X))(Y-E(Y))]=\frac{1}{n-1}\sum_{i=1}^{n}(x_i-\bar{x})(y_i-\bar{y}) Cov(X,Y)=E[(X−E(X))(Y−E(Y))]=n−11i=1∑n(xi−xˉ)(yi−yˉ)
- 方差的计算是针对一维特征的,即针对同一特征不同样本的取值来进行计算得到;而协方差必须要求至少满足二维特征;方差是协方差的特殊情况。
- 方差和协方差的除数是 n − 1 n-1 n−1,这是为了得到方差和协方差的无偏估计。
协方差为正时,说明X和Y是正相关关系;为负时负相关关系;为0时相互独立。 C o v ( X , X ) Cov(X,X) Cov(X,X)就是X的方差。当样本是n维数据时,它们的协方差实际上是协方差矩阵(对称方阵)。
散度矩阵
S = ∑ k = 1 n ( x k − m ) ( x k − m ) T S=\sum_{k=1}^{n}(x_k-m)(x_k-m)^T S=k=1∑n(xk−m)(xk−m)T
其中 m = 1 n ∑ k = 1 n x k m=\frac{1}{n}\sum_{k=1}^{n}x_k m=n1∑k=1nxk
对于数据X的散度矩阵为 X X T XX^T XXT。其实协方差矩阵和散度矩阵关系密切,散度矩阵就是协方差矩阵乘以(总数据量-1)。因此它们的特征值和特征向量是一样的。同时散度矩阵是SVD奇异值分解的一步,因此PCA和SVD有密切关系。
特征值分解矩阵原理
- 特征值与特征向量
如果一个向量v是矩阵A的特征向量,则一定可以表示成下面的形式:
A v = λ v Av=\lambda v Av=λv
其中, λ \lambda λ是特征向量v对应的特征值,一个矩阵的一组特征向量是一组正交向量。 - 特征值分解矩阵
对于矩阵A,有一组特征向量v,将这组向量进行正交化单位化,就能得到一组正交单位向量。特征值分解,就是将矩阵A分解为如下式:
A = Q ∑ Q − 1 A=Q\sum Q^{-1} A=Q∑Q−1
其中,Q是矩阵A的特征向量组成的矩阵, ∑ \sum ∑则是一个对角阵,对角线上的元素就是特征值。
SVD分解矩阵原理
奇异值分解是一个能使用任意矩阵的一种分解的方法,对于任意矩阵A总是存在一个奇异值分解:
A = U ∑ V T A=U\sum V^T A=U∑VT
假设A是一个 m × n m\times n m×n矩阵,那么得到的U是一个 m × m m\times m m×m的方阵,U里面的正交向量被称为左奇异向量。 ∑ \sum ∑是一个 m × n m\times n m×n矩阵, ∑ \sum ∑除了对角线其他元素都为0.对角线上的元素称为奇异值。 V T V^T VT是V的转置矩阵,是一个 n × n n\times n n×n的方阵,它里面的正交向量被称为右奇异值向量。通常 ∑ \sum ∑上的值按从大到小的顺序排列。
SVD算法:
- 求 A A T AA^T AAT的特征值和特征向量,用单位化的特征向量构成U;
- 求 A T A A^TA ATA的特征值和特征向量,用单位化的特征向量构成V;
- 将 A A T AA^T AAT或者 A T A A^TA ATA的特征值求平方根,然后构成 ∑ \sum ∑。
基于特征值分解协方差矩阵实现PCA算法
输入:数据集 X = x 1 , x 2 , x 3 , . . . , x n X={x_1,x_2,x_3,...,x_n} X=x1,x2,x3,...,xn,需要降到k维。
1.去平均值(即去中心化),即每一位特征减去各自的平均值。
2.计算协方差矩阵 1 n X X T \frac{1}{n}XX^T n1XXT,注:这里除或不除样本数量 n n n或 n − 1 n-1 n−1,其实对求出的特征向量没有影响。
3.用特征值分解方法求协方差矩阵 1 n X X T \frac{1}{n}XX^T n1XXT的特征值与特征向量。
4.对特征值从大到小排序,选择其中最大的k个。然后将对应的k个特征向量分别作为行向量组成特征向量矩阵P。
5.将数据转换到k个特征向量构建的新空间中,即 Y = P X Y=PX Y=PX。
基于SVD分解协方差矩阵实现PCA算法
输入:数据集 X = x 1 , x 2 , x 3 , . . . , x n X={x_1,x_2,x_3,...,x_n} X=x1,x2,x3,...,xn,需要降到k维。
1.去平均值(即去中心化),即每一位特征减去各自的平均值。
2.计算协方差矩阵 1 n X X T \frac{1}{n}XX^T n1XXT,注:这里除或不除样本数量 n n n或 n − 1 n-1 n−1,其实对求出的特征向量没有影响。
3.用SVD分解方法求协方差矩阵 1 n X X T \frac{1}{n}XX^T n1XXT的特征值与特征向量。
4.对特征值从大到小排序,选择其中最大的k个。然后将对应的k个特征向量分别作为行向量组成特征向量矩阵。
5.将数据转换到k个特征向量构建的新空间中。
相关文章:

PCA主成分分析算法
在数据分析中,如果特征太多,或者特征之间的相关性太高,通常可以用PCA来进行降维。比如通过对原有10个特征的线性组合, 我们找出3个主成分,就足以解释绝大多数的方差,该算法在高维数据集中被广泛应用。 算法(…...
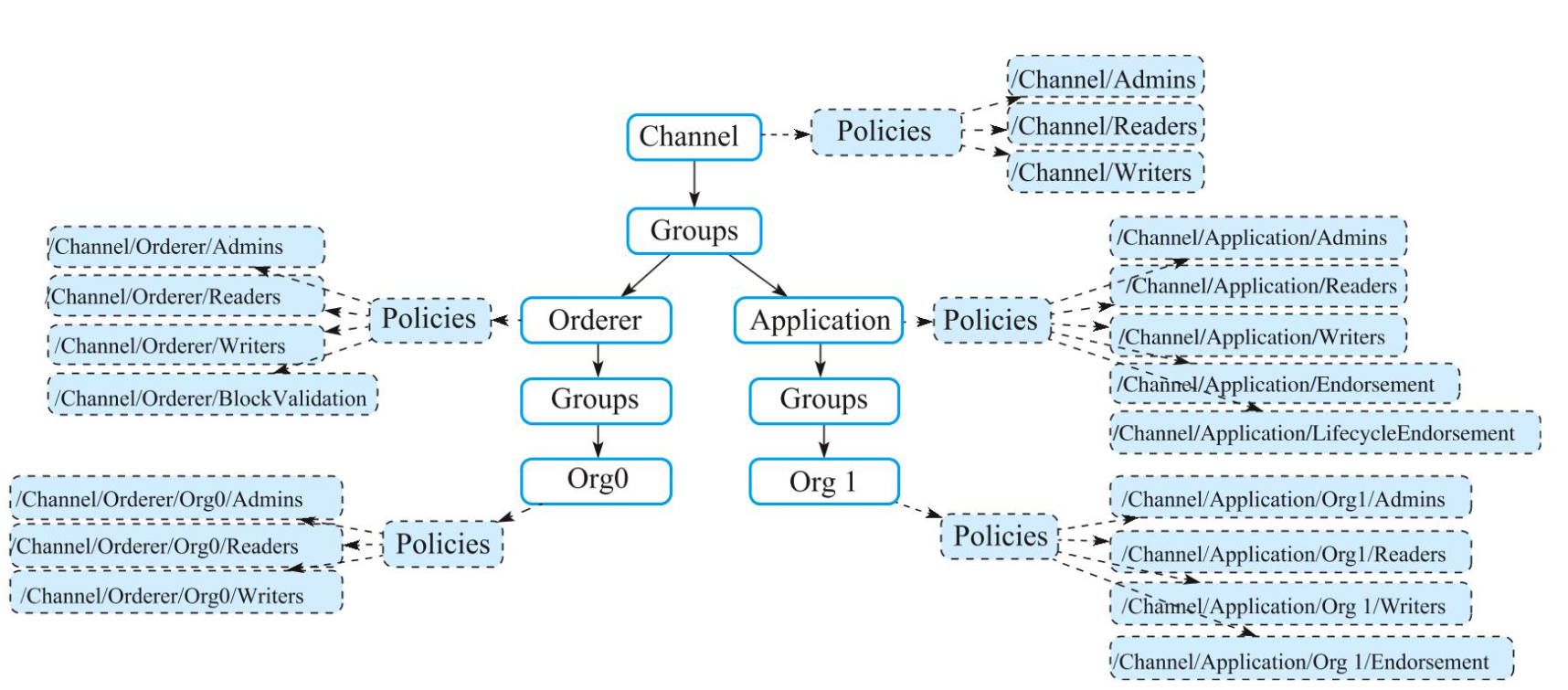
Hyperledger Fabric 权限策略和访问控制
访问控制是区块链网络十分重要的功能,负责控制某个身份在某个场景下是否允许采取某个操作(如读写某个资源)。 常见的访问控制模型包括强制访问控制(Mandatory Access Control)、自主访问控制(Discretionar…...

Day28 回溯算法part04 93. 复原IP地址 78. 子集 90. 子集 II
回溯算法part04 93. 复原IP地址 78. 子集 90. 子集 II 93. 复原 IP 地址 class Solution { private:vector<string> result;bool isValid(string& s,int start,int end){if (start > end) return false;if (s[start] 0 && start ! end) { // 0开头的数…...

Linux系统常用的安全优化
环境:CentOS7.9 1、禁用SELinux SELinux是美国国家安全局对于强制访问控制的实现 1)永久禁用SELinux vim /etc/selinux/config SELINUXdisabled #必须重启系统才能生效2)临时禁用SELInux getenforce #查看SELInux当前状态 setenforce 0 #数字…...
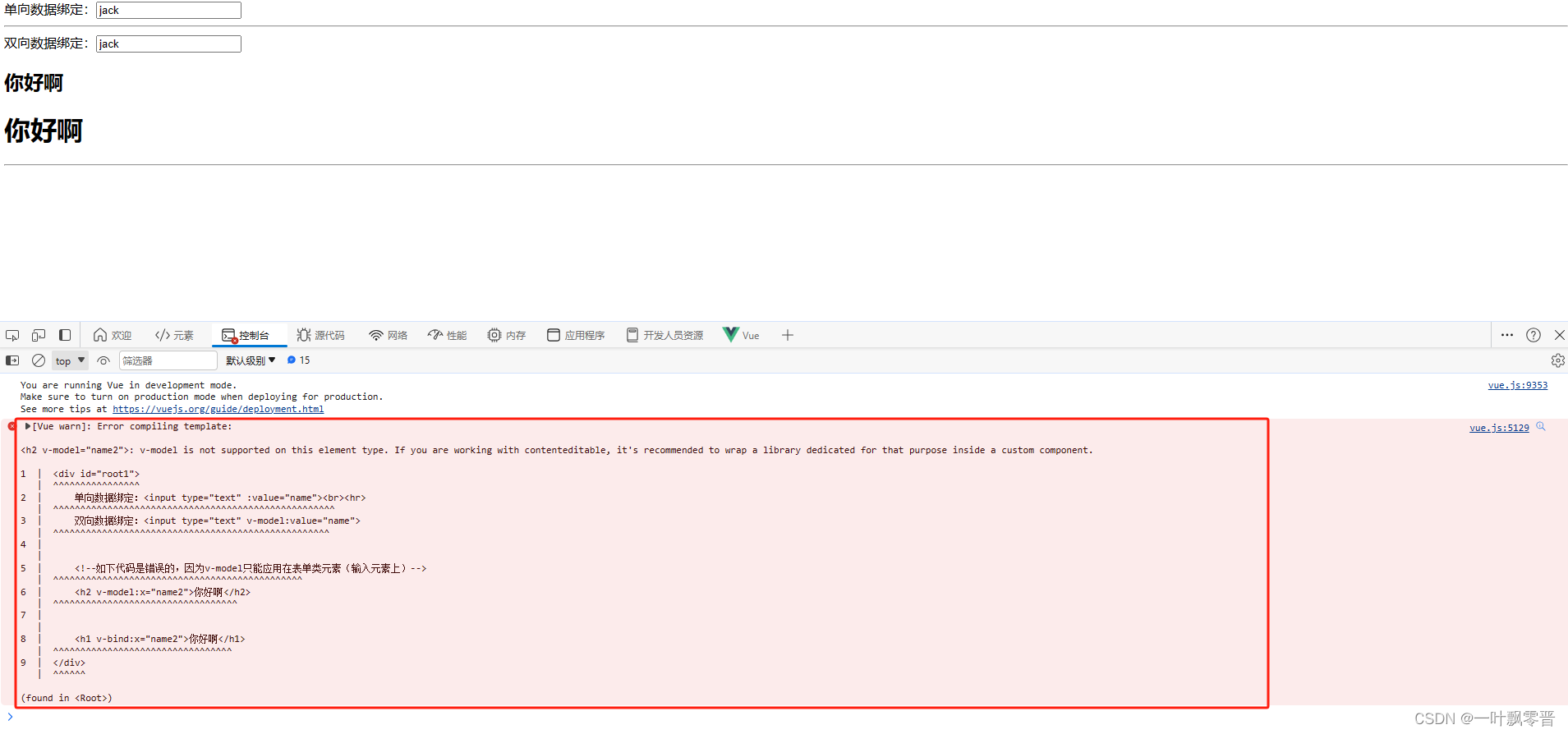
Vue-4、单向数据绑定与双向数据绑定
1、单向数据绑定 <!DOCTYPE html> <html lang"en"> <head><meta charset"UTF-8"><title>数据绑定</title><!--引入vue--><script type"text/javascript" src"https://cdn.jsdelivr.net/npm/…...

【Flutter 开发实战】Dart 基础篇:常用运算符
在Dart中,运算符是编写任何程序的基本构建块之一。本文将详细介绍Dart中常用的运算符,以帮助初学者更好地理解和运用这些概念。 1. 算术运算符 算术运算符用于执行基本的数学运算。Dart支持常见的加、减、乘、除、整除以及取余运算。常见的算数运算符如…...

C++:ifstream通过getline读取文件会忽略最后一行空行
getline是读取文件的常用函数,虽然使用简单,但是有一个较容易被忽视的问题,就是文件最后一行空行会被忽略。 #include <iostream> #include <fstream> #include <string> using namespace std;void readWholeFileWithGetline(string fileName) {string t…...

力扣123. 买卖股票的最佳时机 III
动态规划 思路: 最多可以完成两笔交易,因此任意一天结束后,会处于5种状态: 未进行任何操作;只进行了一次买操作;进行了一次买操作和一次卖操作;再完成了一次交易之后,进行了一次买操…...

Vue3:vue-cli项目创建
一、node.js检测或安装: node -v node.js官方 二、vue-cli安装: npm install -g vue/cli # OR yarn global add vue/cli/*如果安装的时候报错,可以尝试一下方法 删除C:\Users**\AppData\Roaming下的npm和npm-cache文件夹 删除项目下的node…...

C# .Net学习笔记—— 异步和多线程(Task)
一、概念 Task是DotNet3.0之后所推出的一种新的使用多线程的方式,它是基于ThreadPool线程进行封装的。 二、使用多线程的时机 任务能够并发运行的时候,提升速度;优化体验 三、基本使用方法 private void button5_Click(object sender, Ev…...
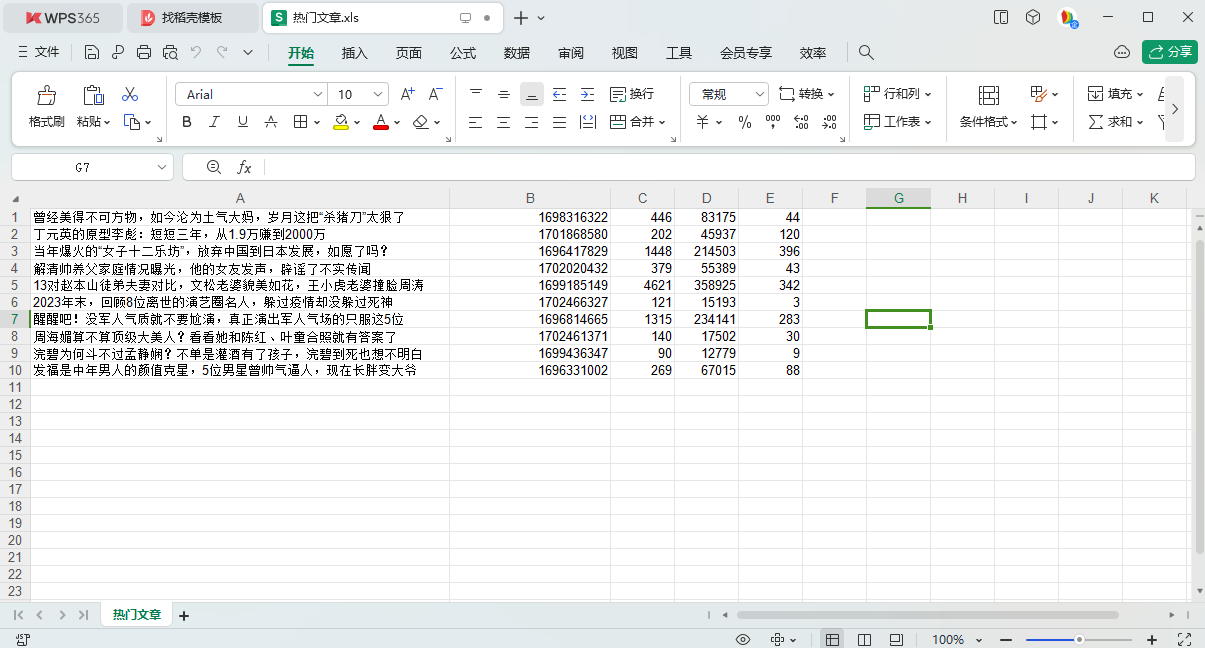
Python从入门到网络爬虫(读写Excel详解)
前言 Python操作Excel的模块有很多,并且各有优劣,不同模块支持的操作和文件类型也有不同。最常用的Excel处理库有xlrd、xlwt、xlutils、xlwings、openpyxl、pandas,下面是各个模块的支持情况: 工具名称.xls.xlsx获取文件内容写入…...
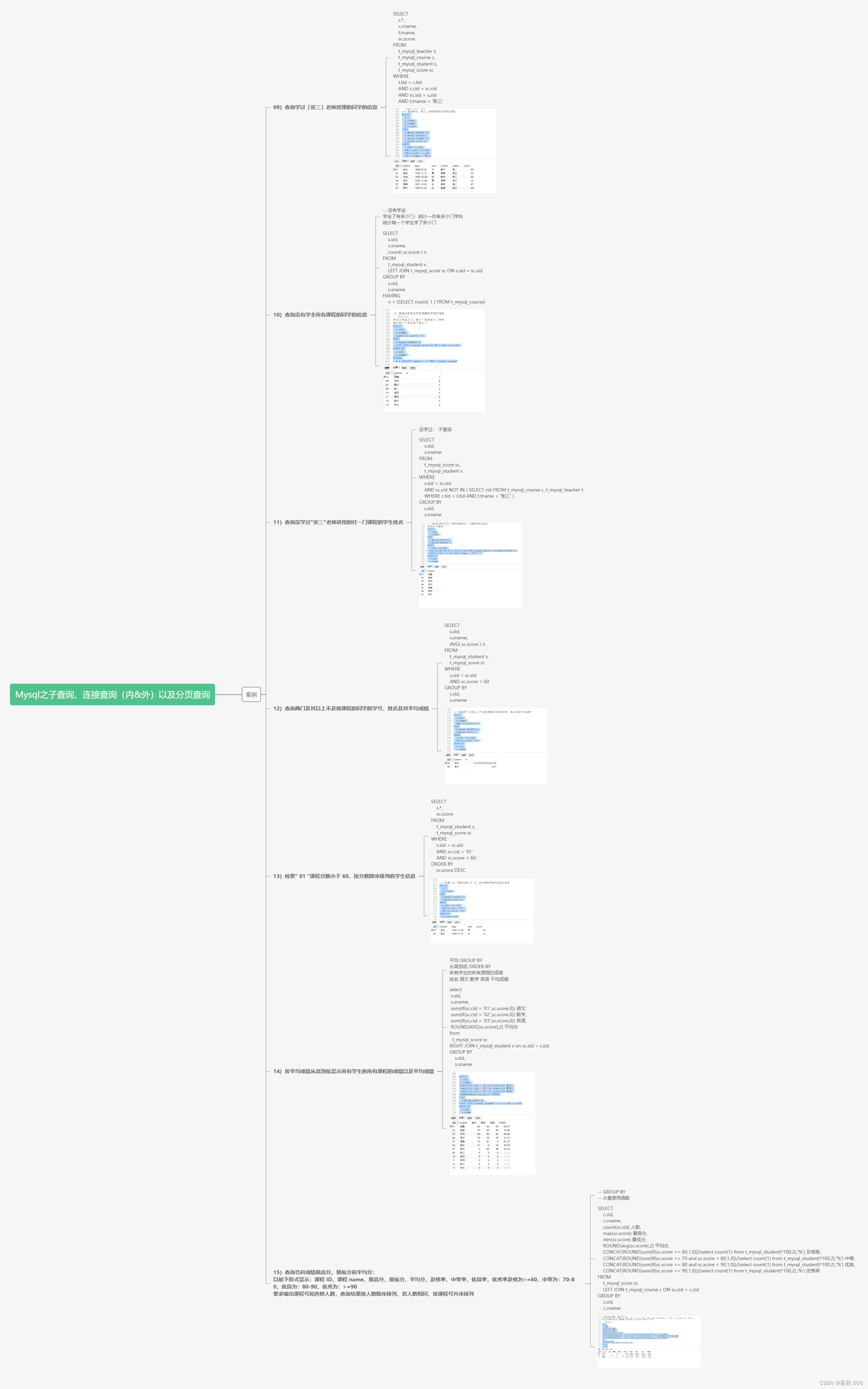
Mysql之子查询、连接查询(内外)以及分页查询
目录 一.案例(接上篇博客) 09)查询学过「张三」老师授课的同学的信息 10)查询没有学全所有课程的同学的信息 11)查询没学过"张三"老师讲授的任一门课程的学生姓名 12)查询两门及其以上不及格课程…...

计算机的存储单位
在计算机中,只能识别二进制。 byte是1个字节,是8个比特位,所以byte可以存储的最大值是:01111111,byte是 [-128 ~ 127] 共可以标识256个不同的数字。 1字节 8bit(8比特)--> 1byte 8bit 类…...

设备树文件中的设备节点
一. 简介 前面几篇文章学习了 关于设备树文件的编译,设备树文件的调用。 本文开始学习 设备树文件的语法。具体学习设备节点与标准属性。 二. 设备树文件之设备节点与标准属性 1. 设备节点 设备树 是采用树形结构来描述板子上的设备信息的文件,每…...

文件管理工具.netcore资源文件管理
文件管理工具 怎么快速有效的管理我的文件包括文件夹,需求功能是 模糊搜索显示匹配的文件夹或文件数据 快速打开文件夹位置 在windows直接查看搜索速度太慢,范围宽泛,整理所需资源文件名和文件本机路径保存在数据库,可以在数据库中…...

go-carbon v2.3.4 发布,轻量级、语义化、对开发者友好的 Golang 时间处理库
carbon 是一个轻量级、语义化、对开发者友好的 golang 时间处理库,支持链式调用。 目前已被 awesome-go 收录,如果您觉得不错,请给个 star 吧 github.com/golang-module/carbon gitee.com/golang-module/carbon 安装使用 Golang 版本大于…...

vue3 内置组件
文章目录 前言一、过渡效果相关的组件1、Transition2、TransitionGroup 二、状态缓存组件(KeepAlive)三、传送组件(Teleport )四、异步依赖处理组件(Suspense) 前言 在vue3中 其提供了5个内置组件 Transiti…...

MFC如何动态创建button按钮并添加点击事件
在MFC中,可以使用CButton类来动态创建按钮。下面是一个示例代码,演示了如何动态创建按钮并添加点击事件: 在对话框类的头文件中声明按钮变量: CButton m_btnDynamic;在对话框的OnInitDialog()函数中使用Create()函数创建按钮&am…...
Qt - QML框架
文章目录 1 . 前言2 . 框架生成3 . 框架解析3.1 qml.pro解析3.2 main.cpp解析3.3 main.qml解析 4 . 总结 【极客技术传送门】 : https://blog.csdn.net/Engineer_LU/article/details/135149485 1 . 前言 什么是QML? QML是一种用户界面规范和编程语言。它允许开发人员…...
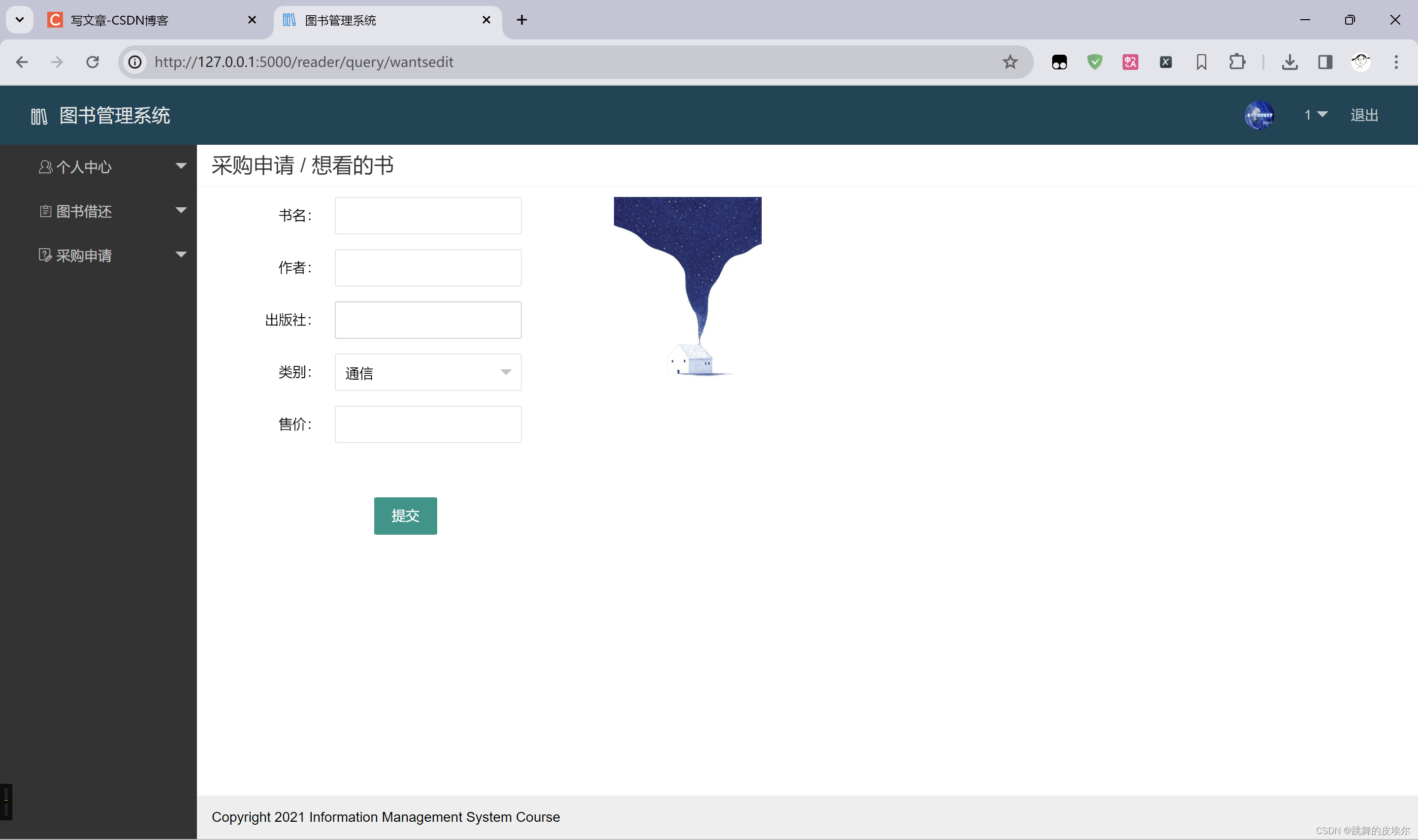
Python+Flask+MySQL的图书馆管理系统【附源码,运行简单】
PythonFlaskMySQL的图书馆管理系统【附源码,运行简单】 总览 1、《的图书馆管理系统》1.1 方案设计说明书设计目标需求分析工具列表 2、详细设计2.1 登录2.2 注册2.3 程序主页面2.4 图书新增界面2.5 图书信息修改界面2.6 普通用户界面2.7 其他功能贴图 3、下载 总览…...

vscode里如何用git
打开vs终端执行如下: 1 初始化 Git 仓库(如果尚未初始化) git init 2 添加文件到 Git 仓库 git add . 3 使用 git commit 命令来提交你的更改。确保在提交时加上一个有用的消息。 git commit -m "备注信息" 4 …...

Appium+python自动化(十六)- ADB命令
简介 Android 调试桥(adb)是多种用途的工具,该工具可以帮助你你管理设备或模拟器 的状态。 adb ( Android Debug Bridge)是一个通用命令行工具,其允许您与模拟器实例或连接的 Android 设备进行通信。它可为各种设备操作提供便利,如安装和调试…...

Leetcode 3577. Count the Number of Computer Unlocking Permutations
Leetcode 3577. Count the Number of Computer Unlocking Permutations 1. 解题思路2. 代码实现 题目链接:3577. Count the Number of Computer Unlocking Permutations 1. 解题思路 这一题其实就是一个脑筋急转弯,要想要能够将所有的电脑解锁&#x…...

uniapp中使用aixos 报错
问题: 在uniapp中使用aixos,运行后报如下错误: AxiosError: There is no suitable adapter to dispatch the request since : - adapter xhr is not supported by the environment - adapter http is not available in the build 解决方案&…...

多种风格导航菜单 HTML 实现(附源码)
下面我将为您展示 6 种不同风格的导航菜单实现,每种都包含完整 HTML、CSS 和 JavaScript 代码。 1. 简约水平导航栏 <!DOCTYPE html> <html lang"zh-CN"> <head><meta charset"UTF-8"><meta name"viewport&qu…...

蓝桥杯 冶炼金属
原题目链接 🔧 冶炼金属转换率推测题解 📜 原题描述 小蓝有一个神奇的炉子用于将普通金属 O O O 冶炼成为一种特殊金属 X X X。这个炉子有一个属性叫转换率 V V V,是一个正整数,表示每 V V V 个普通金属 O O O 可以冶炼出 …...

JVM 内存结构 详解
内存结构 运行时数据区: Java虚拟机在运行Java程序过程中管理的内存区域。 程序计数器: 线程私有,程序控制流的指示器,分支、循环、跳转、异常处理、线程恢复等基础功能都依赖这个计数器完成。 每个线程都有一个程序计数…...

[免费]微信小程序问卷调查系统(SpringBoot后端+Vue管理端)【论文+源码+SQL脚本】
大家好,我是java1234_小锋老师,看到一个不错的微信小程序问卷调查系统(SpringBoot后端Vue管理端)【论文源码SQL脚本】,分享下哈。 项目视频演示 【免费】微信小程序问卷调查系统(SpringBoot后端Vue管理端) Java毕业设计_哔哩哔哩_bilibili 项…...

CSS | transition 和 transform的用处和区别
省流总结: transform用于变换/变形,transition是动画控制器 transform 用来对元素进行变形,常见的操作如下,它是立即生效的样式变形属性。 旋转 rotate(角度deg)、平移 translateX(像素px)、缩放 scale(倍数)、倾斜 skewX(角度…...

WPF八大法则:告别模态窗口卡顿
⚙️ 核心问题:阻塞式模态窗口的缺陷 原始代码中ShowDialog()会阻塞UI线程,导致后续逻辑无法执行: var result modalWindow.ShowDialog(); // 线程阻塞 ProcessResult(result); // 必须等待窗口关闭根本问题:…...
