PTA✨C语言 组合数的和
7-5 组合数的和
分数 15
全屏浏览题目
切换布局
作者 陈越
单位 浙江大学
给定 N 个非 0 的个位数字，用其中任意 2 个数字都可以组合成 1 个 2 位的数字。要求所有可能组合出来的 2 位数字的和。例如给定 2、5、8，则可以组合出：25、28、52、58、82、85，它们的和为330。
输入格式：
输入在一行中先给出 N（1 < N < 10），随后一行给出 N 个不同的非 0 个位数字。数字间以空格分隔。
输出格式：
输出所有可能组合出来的2位数字的和。
输入样例：
3
2 8 5
输出样例：
330
代码长度限制
16 KB
时间限制
400 ms
内存限制
64 MB
相关文章：
PTA✨C语言 组合数的和
7-5 组合数的和 分数 15 全屏浏览题目 切换布局 作者 陈越 单位 浙江大学 给定 N 个非 0 的个位数字，用其中任意 2 个数字都可以组合成 1 个 2 位的数字。要求所有可能组合出来的 2 位数字的和。例如给定 2、5、8，则可以组合出：25、28、5…...
这些开源自动化测试框架，会用等于白嫖一个w
作者：黑马测试 链接：https://www.zhihu.com/question/19923336/answer/2585952461 来源：知乎 著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。 随着计算机技术人员的大量增加，通过编写代码来…...
代码随想录第三十六天——无重叠区间，划分字母区间，合并区间
leetcode 435. 无重叠区间 题目链接：无重叠区间 方法一：按右边界排序 按照右边界排序，从左向右记录非交叉区间的个数。最后用区间总数减去非交叉区间的个数就是需要移除的区间个数。此时问题转化为求非交叉区间的最大个数。 版本一&#…...
Python数据分析：入门到实践
一、引言 （用手机写的，明天重新排版。） 在当今数据驱动的时代，数据分析已经成为各行各业不可或缺的一部分。Python作为一种高效、易学的编程语言，在数据分析领域具有广泛的应用。本文将带你从Python数据分析的入门知…...
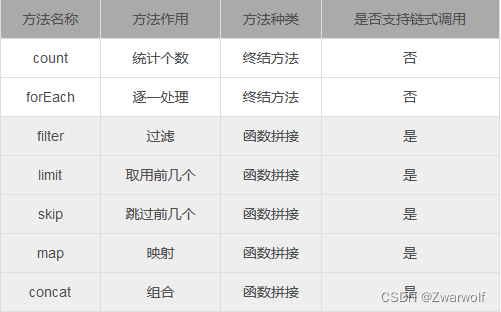
第7章-第9节-Java中的Stream流（链式调用）
1、什么是Stream流 Lambda表达式，基于Lambda所带来的函数式编程，又引入了一个全新的Stream概念，用于解决集合类库既有的鼻端。 2、案例 假设现在有一个需求， 将list集合中姓张的元素过滤到一个新的集合中；然后将过滤…...
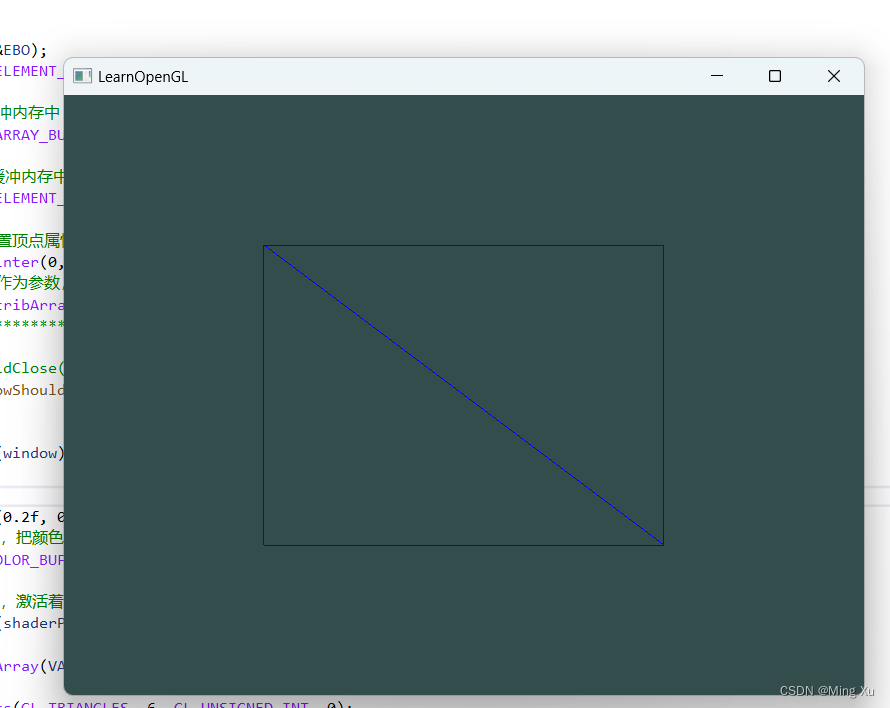
创建一个矩形中有两个三角形
#include <glad/glad.h> #include <GLFW/glfw3.h>#include <iostream>float vertices[] {// 第一个三角形0.5f, 0.5f, 0.0f, // 右上0.5f, -0.5f, 0.0f, // 右下-0.5f, -0.5f, 0.0f, // 左下-0.5f, 0.5f, 0.0f, // 左上 };unsigned i…...
Open3D 基于kdtree树的邻近点搜索（10）
Open3D 基于kdtree树的邻近点搜索（10） 一、算法简介二、算法实现1.K邻近点搜索2.R邻域点搜索三、结果释义一、算法简介 KD 树（k-dimensional tree）是一种用于组织 k 维空间中点的数据结构，旨在提供高效的 k 最近邻搜索和范围搜索（如半径邻域搜索）。KD 树通过递归地将空间…...
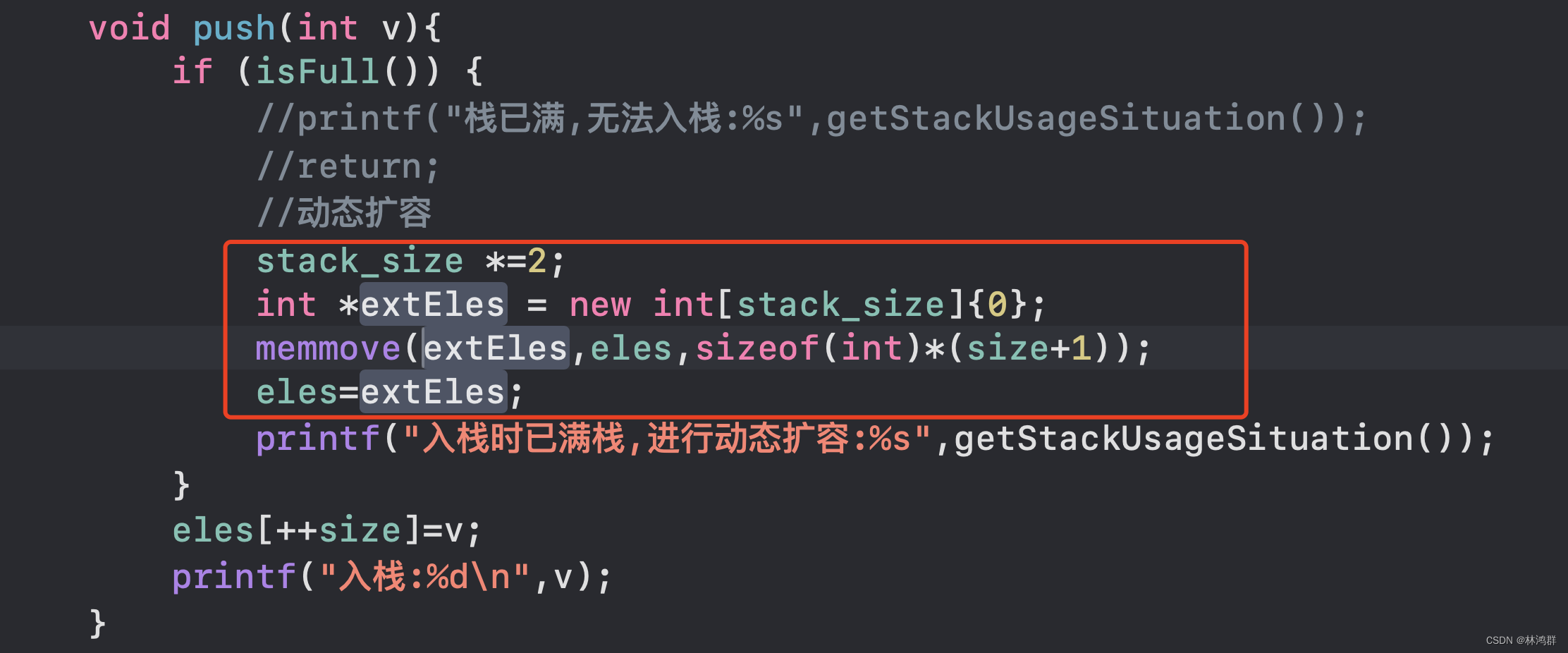
c++实现支持动态扩容的栈(stack)
1.在栈容量满时自动扩容: 支持自动扩容栈实现: // // myStack.hpp // algo_demo // // Created by Hacker X on 2024/1/9. //#ifndef myStack_hpp #define myStack_hpp #include <stdio.h> #include <string.h> //栈实现 //1.入栈 //2.出栈 //3.空栈 //4.满栈 …...
举例说明计算机视觉（CV）技术的优势和挑战。
计算机视觉（Computer Vision，CV）技术是指使计算机能够理解和解释视觉数据的能力。CV技术在很多领域都有广泛的应用，包括图像处理、目标检测、人脸识别、自动驾驶等。以下是CV技术的一些优势和挑战的例子： 优势&#x…...
如何利用docker来部署war包项目
首先编写dockerfile文件： # 使用官方的Tomcat镜像作为基础镜像 FROM tomcat:9.0# 将war包复制到容器的webapps目录下 COPY xxxx.war /usr/local/tomcat/webapps/# 暴露Tomcat的默认端口 EXPOSE 8080 编写docker-compose.yml文件： version: 3 services…...
SpringBoot 如何增强PageHelper入参的健壮性
PageHelper.startPage(int pageNum, int pageSize, boolean count) 参数为外部输入，故存在异常输入场景。比如 pageNum 和 pageSize 输入的值 负数 或者 0，所以引入PageUtils来对入参进行判断矫正，从而避免引入异常。 第1步：支持…...
书生·浦语大模型全链路开源体系 学习笔记 第三课
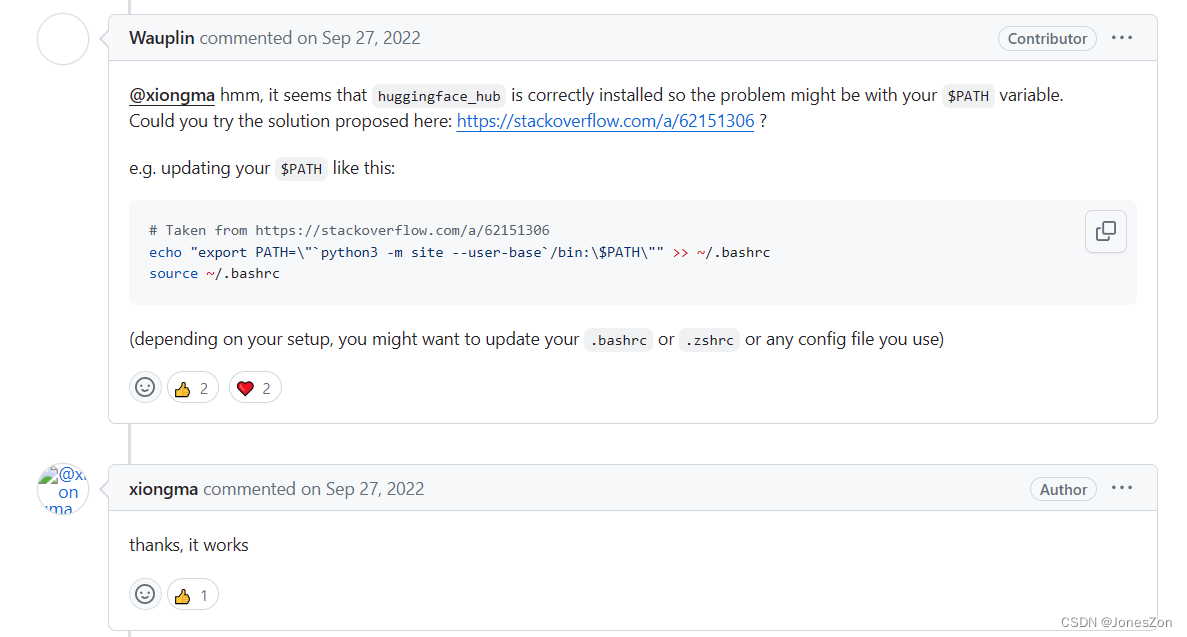
huggingface-cli: command not found 按照该文档解决即可 https://github.com/huggingface/huggingface_hub/issues/1079 具体如下： 1、确保环境已将安装huggingface-cli 2、版本需要旧版，pip install huggingface_hub0.20.1 3、再按如下执行 # T…...
CodeGPT，你的智能编码助手—CSDN出品
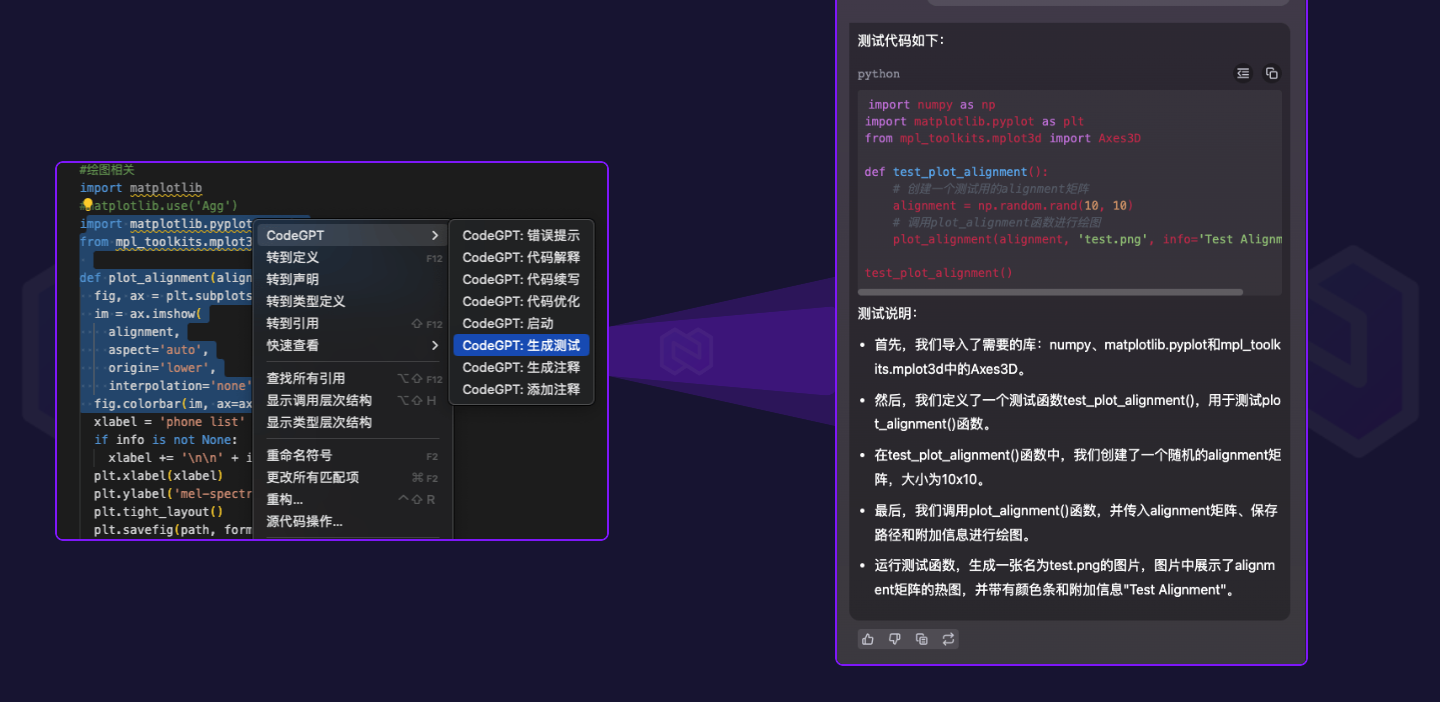
CodeGPT是由CSDN打造的一款生成式AI产品，专为开发者量身定制。 无论是在学习新技术还是在实际工作中遇到的各类计算机和开发难题，CodeGPT都能提供强大的支持。其涵盖的功能包括代码优化、续写、解释、提问等，还能生成精准的注释和创作相关内…...
VMware Workstation——修改虚拟机配置和设置网络
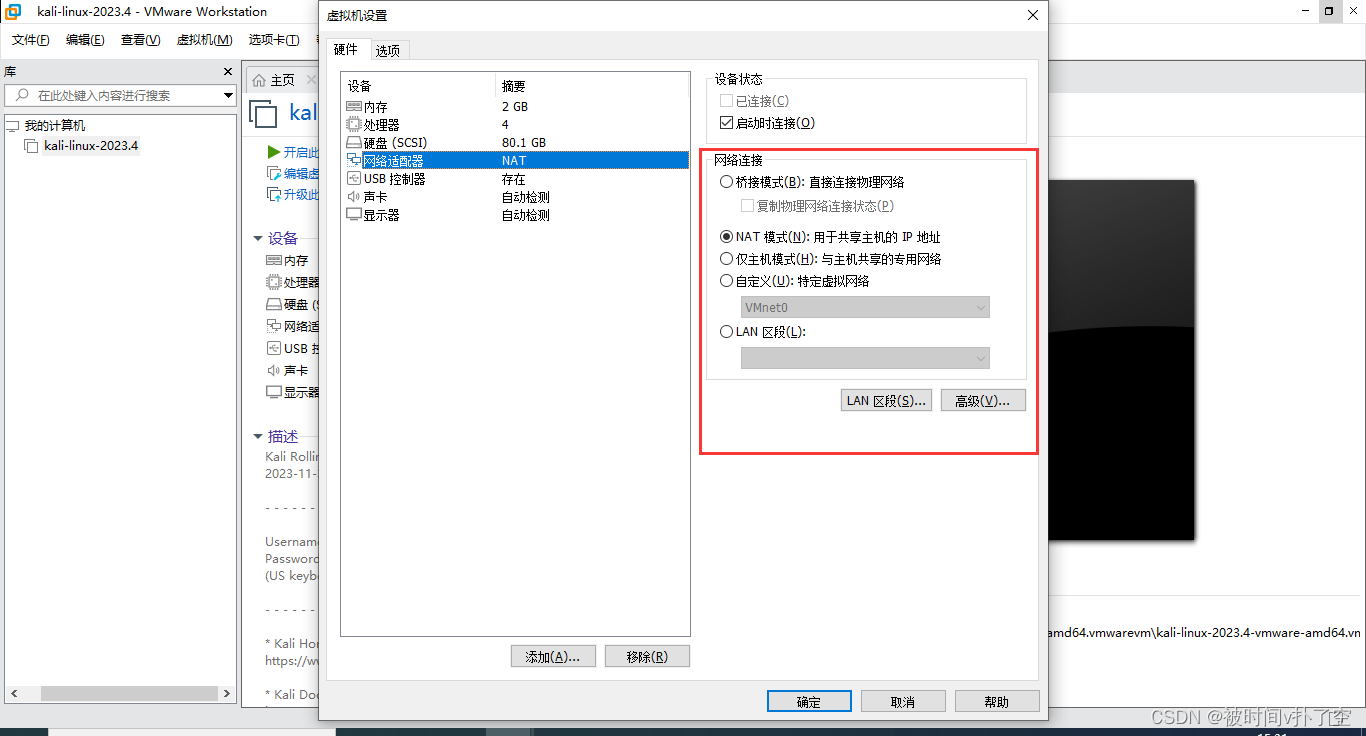
目录 一、修改配置 1、点击需要修改配置的虚拟机，然后点击编辑虚拟机配置 2、修改内存、CPU、硬盘配置 二、设置网络 1、从虚拟机配置中进入到网络适配器设置 2、选择网络连接模式 一、修改配置 1、点击需要修改配置的虚拟机，然后点击编辑虚拟机配…...
计算机毕业设计 基于SpringBoot的项目申报系统的设计与实现 Java实战项目 附源码+文档+视频讲解
博主介绍：✌从事软件开发10年之余，专注于Java技术领域、Python人工智能及数据挖掘、小程序项目开发和Android项目开发等。CSDN、掘金、华为云、InfoQ、阿里云等平台优质作者✌ 🍅文末获取源码联系🍅 👇🏻 精…...
CentOS 7.8 安装 Docker
1.卸载旧版本 sudo yum remove docker \ docker-client \ docker-client-latest \ docker-common \ docker-latest \ docker-latest-logrotate \ docker-logrotate \ docker-engine2.安装依赖 sudo yum -y install gcc sudo yum -y install gcc-c3.安装软件包 sudo yum inst…...
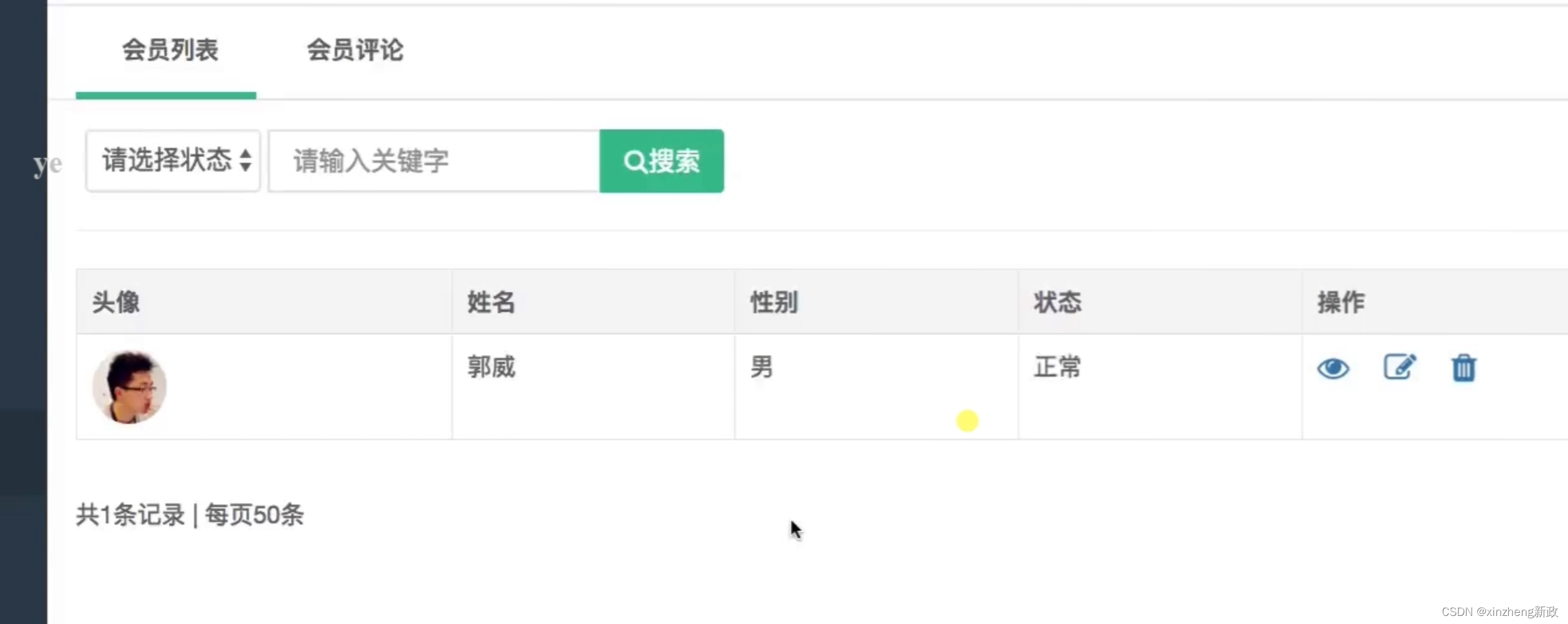
Flask 会员列表展示
感谢编程浪子师傅的源码信息分享 web/controllers/member/Member.py # -*- coding: utf-8 -*- from flask import Blueprint,request,redirect,jsonify from common.libs.Helper import ops_render,iPagination,getCurrentDate,getDictFilterField,selectFilterObj from comm…...
光纤知识总结
1光纤概念： 光导纤维（英语：Optical fiber），简称光纤，是一种由玻璃或塑料制成的纤维，利用光在这些纤维中以全内反射原理传输的光传导工具。 微细的光纤封装在塑料护套中，使得它能够…...
LeetCode简单题记录
1、两数之和，给定数组nums，求和为target的两个数组元素的下标 我用了两个for循环，官方解为 哈希表，知识盲区 class Solution { public:vector<int> twoSum(vector<int>& nums, int target) {unordered_map<i…...
【Python学习】Python学习10-列表
目录 【Python学习】Python学习10-列表 前言创建语法访问列表中的值更新和删除列表元素操作列表列表截取Python列表函数&方法参考 文章所属专区 Python学习 前言 本章节主要说明Python的列表List。 创建语法 创建一个列表 通过方括号和逗号分割创建，列表数据…...
eNSP-Cloud(实现本地电脑与eNSP内设备之间通信)
说明： 想象一下，你正在用eNSP搭建一个虚拟的网络世界，里面有虚拟的路由器、交换机、电脑（PC）等等。这些设备都在你的电脑里面“运行”，它们之间可以互相通信，就像一个封闭的小王国。 但是&#…...
Chapter03-Authentication vulnerabilities
文章目录 1. 身份验证简介1.1 What is authentication1.2 difference between authentication and authorization1.3 身份验证机制失效的原因1.4 身份验证机制失效的影响 2. 基于登录功能的漏洞2.1 密码爆破2.2 用户名枚举2.3 有缺陷的暴力破解防护2.3.1 如果用户登录尝试失败次…...
synchronized 学习
学习源： https://www.bilibili.com/video/BV1aJ411V763?spm_id_from333.788.videopod.episodes&vd_source32e1c41a9370911ab06d12fbc36c4ebc 1.应用场景 不超卖，也要考虑性能问题（场景） 2.常见面试问题： sync出…...
设计模式和设计原则回顾
设计模式和设计原则回顾 23种设计模式是设计原则的完美体现，设计原则设计原则是设计模式的理论基石， 设计模式 在经典的设计模式分类中（如《设计模式：可复用面向对象软件的基础》一书中），总共有23种设计模式，分为三大类： 一、创建型模式（5种） 1. 单例模式（Sing…...
ES6从入门到精通：前言
ES6简介 ES6（ECMAScript 2015）是JavaScript语言的重大更新，引入了许多新特性，包括语法糖、新数据类型、模块化支持等，显著提升了开发效率和代码可维护性。 核心知识点概览 变量声明 let 和 const 取代 var…...
` 方法)
深入浅出：JavaScript 中的 `window.crypto.getRandomValues()` 方法
深入浅出：JavaScript 中的 window.crypto.getRandomValues() 方法 在现代 Web 开发中，随机数的生成看似简单，却隐藏着许多玄机。无论是生成密码、加密密钥，还是创建安全令牌，随机数的质量直接关系到系统的安全性。Jav…...
Leetcode 3577. Count the Number of Computer Unlocking Permutations
Leetcode 3577. Count the Number of Computer Unlocking Permutations 1. 解题思路2. 代码实现 题目链接：3577. Count the Number of Computer Unlocking Permutations 1. 解题思路 这一题其实就是一个脑筋急转弯，要想要能够将所有的电脑解锁&#x…...
Python爬虫（一）：爬虫伪装
一、网站防爬机制概述 在当今互联网环境中，具有一定规模或盈利性质的网站几乎都实施了各种防爬措施。这些措施主要分为两大类： 身份验证机制：直接将未经授权的爬虫阻挡在外反爬技术体系：通过各种技术手段增加爬虫获取数据的难度…...
IoT/HCIP实验-3/LiteOS操作系统内核实验(任务、内存、信号量、CMSIS..)
文章目录 概述HelloWorld 工程C/C配置编译器主配置Makefile脚本烧录器主配置运行结果程序调用栈 任务管理实验实验结果osal 系统适配层osal_task_create 其他实验实验源码内存管理实验互斥锁实验信号量实验 CMISIS接口实验还是得JlINKCMSIS 简介LiteOS->CMSIS任务间消息交互…...
用docker来安装部署freeswitch记录
今天刚才测试一个callcenter的项目，所以尝试安装freeswitch 1、使用轩辕镜像 - 中国开发者首选的专业 Docker 镜像加速服务平台 编辑下面/etc/docker/daemon.json文件为 {"registry-mirrors": ["https://docker.xuanyuan.me"] }同时可以进入轩…...