当前位置： 首页 > news >正文

超维空间M1无人机使用说明书——21、基于opencv的人脸识别

news 2025/12/17 12:24:43

引言：M1型号无人机不仅提供了yolo进行物体识别，也增加了基于opencv的人脸识别功能包，仅需要启动摄像头和识别节点即可

链接: 源码链接

一、一键启动摄像头和人脸识别节点

roslaunch robot_bringup bringup_face_detect.launch
无报错，出现以下界面表示启动成功。

在这里插入图片描述在这里插入图片描述

launch文件详解

在这里插入图片描述

二、查看摄像头的图像

为了节约资源，默认关闭了图像显示框，如果需要查看相关图像信息，可以通过rqt工具查看图像信息

步骤一、终端输入：

rqt_image_view

注意：再出现以上图框的时候，选择/cv_bridge_image作为订阅的话题

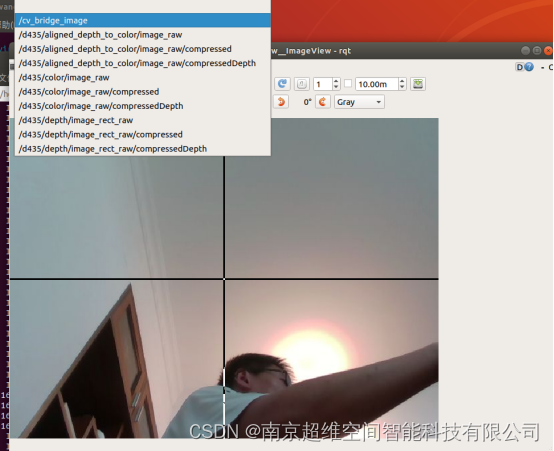
在这里插入图片描述

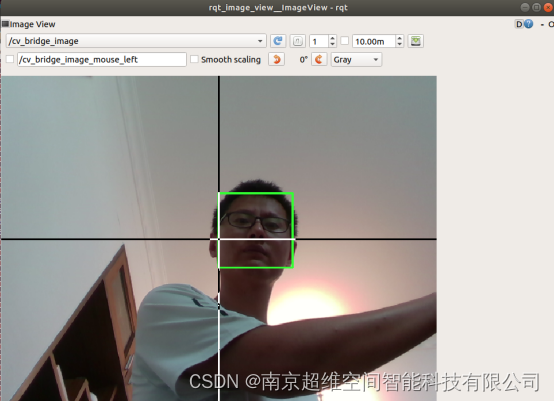
步骤二、查看人脸识别效果

当人脸出现在摄像头的视野范围内，人脸部分将会被框选出来。

在这里插入图片描述

相关文章：

超维空间M1无人机使用说明书——21、基于opencv的人脸识别

引言：M1型号无人机不仅提供了yolo进行物体识别，也增加了基于opencv的人脸识别功能包，仅需要启动摄像头和识别节点即可 链接: 源码链接 一、一键启动摄像头和人脸识别节点 roslaunch robot_bringup bringup_face_detect.launch无报错&#…...

编程日记 2024/1/10 7:58:55

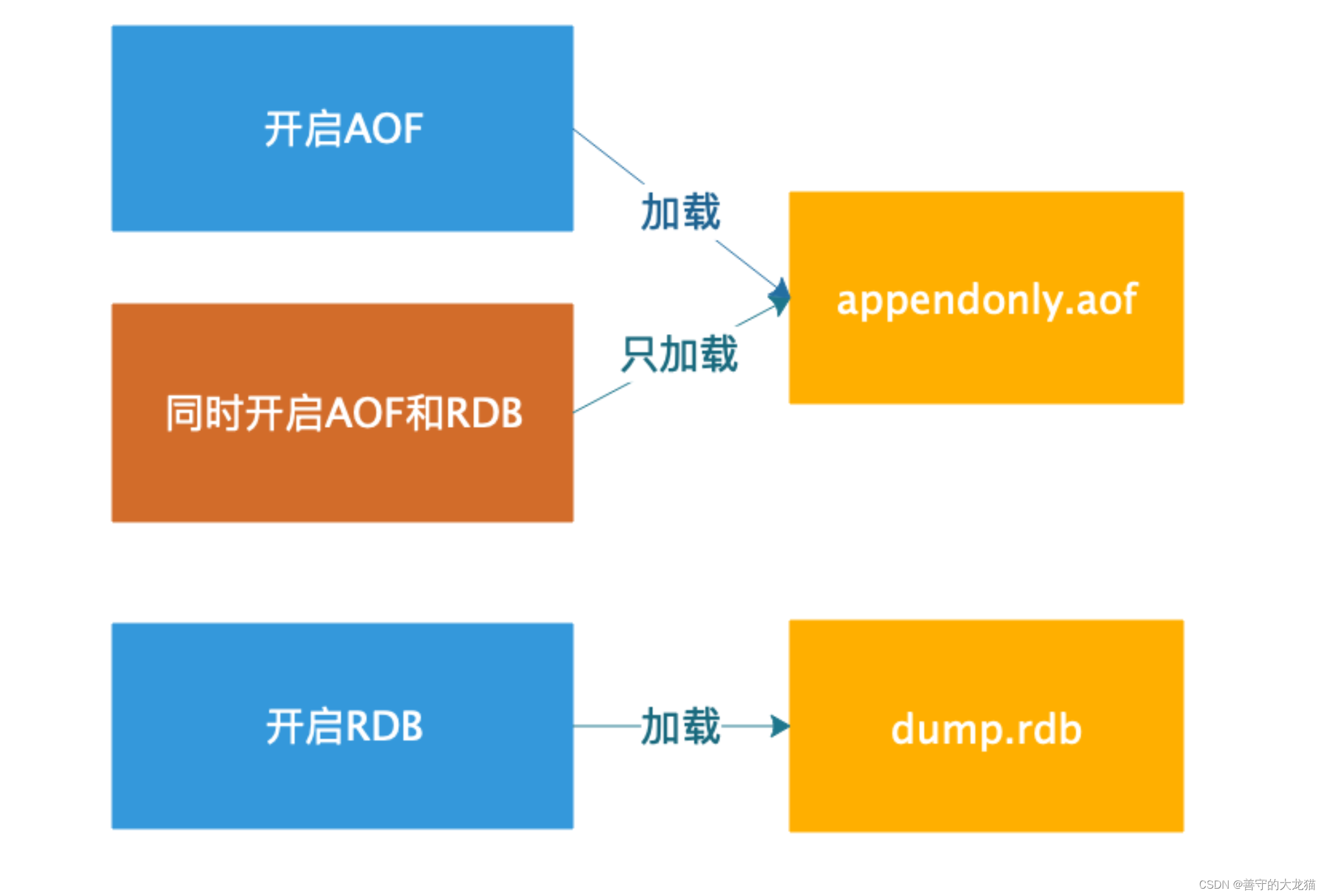
Redis 持久化——AOF

文章目录 为什么需要AOF?概念持久化查询和设置1. 查询AOF启动状态2. 开启AOF持久化2.1 命令行启动AOF2.2 配置文件启动 AOF 3. 触发持久化3.1 自动触发3.3 手动触发 4. AOF 文件重写4.1 什么是AOF重写？4.2 AOF 重写实现4.3 AOF 重写流程 5. 配置说明6. 数据恢复6.1…...

编程日记 2024/1/10 7:57:54

华为云服务介绍（二）

在 华为云服务介绍（一） 中我们看到华为云提供了一系列的云服务，包括计算、存储、网络、数据库、安全等方面的解决方案。通过灵活的系统架构设计，可以充分利用这些云服务技术，从而更好地满足用户的需求。 本文从系统架构的角度出发，通过充分利用华为云提供的各种云服务技…...

编程日记 2024/1/10 7:55:52

mysql列题

mysql列题 1.查询学过「张三」老师授课的同学的信息2.查询没有学全所有课程的同学的信息3.查询没学过"张三"老师讲授的任一门课程的学生姓名4.查询两门及其以上不及格课程的同学的学号，姓名及其平均成绩5.检索" 01 "课程分数小于 60&#xff0c…...

编程日记 2024/1/10 7:53:50

cpu缓存一致性

文章目录 cpu缓存一致性缓存的出现：多核之后带来的缓存一致性问题，如何解决LOCK 指令（刚好可以实现上述的目标）LOCK 指令特性内存屏障特性编译器屏障的作用MESI协议为什么有了 MESI协议 还需要 内存屏障问题：总结&…...

编程日记 2024/1/10 7:52:49

Android Framework 常见解决方案（25-1）定制CPUSET解决方案-framework部分修改

1 原理说明 这个方案有如下基本需求： 构建自定义CPUSET，/dev/cpuset中包含一个全新的cpuset分组。且可以通过set_cpuset_policy和set_sched_policy接口可以设置自定义CPUSET。开机启动后可以通过zygote判定来对特定的应用进程设置CPUSET，并…...

编程日记 2024/1/10 7:51:48

PyTorch 参数化深度解析：自定义、管理和优化模型参数

目录 torch.nn子模块parametrize parametrize.register_parametrization 主要特性和用途 使用场景 参数和关键字参数 注意事项 示例 parametrize.remove_parametrizations 功能和用途 参数 返回值 异常 使用示例 parametrize.cached 功能和用途 如何使用 示例…...

编程日记 2024/1/10 7:48:45

自承载 Self-Host ASP.NET Web API 1 (C#)

本教程介绍如何在控制台应用程序中托管 Web API。 ASP.NET Web API不需要 IIS。 可以在自己的主机进程中自托管 Web API。 创建控制台应用程序项目 启动 Visual Studio，然后从“开始”页中选择“新建项目”。 或者，从“ 文件 ”菜单中选择“ 新建 ”&a…...

编程日记 2024/1/10 7:47:44

Vue2-子传父和父传子的基本用法

在Vue 2中，可以使用props和$emit来实现子组件向父组件传值（子传父）和父组件向子组件传值（父传子）。 子传父（子组件向父组件传值）的基本用法如下： 在父组件中定义一个属性&#xff…...

编程日记 2024/1/10 7:46:43

使用numpy处理图片——镜像翻转和旋转

在《使用numpy处理图片——基础操作》一文中，我们介绍了如何使用numpy修改图片的透明度。本文我们将介绍镜像翻转和旋转。 镜像翻转 上下翻转 from PIL import Image import numpy as np img Image.open(example.png) data np.array(img)# axis0 is vertical, a…...

编程日记 2024/1/10 7:41:38

HTML5 article标签，＜time＞...＜/time＞标签和pubdate属性的运用

1、<article>...</article>标签的运用 article标签代表文档、页面或应用程序中独立的、完整的、可以独自被外部引用的内容。它可以是一篇博客或报竟杂志中的文章、一篇论坛帖子、一段用户评论或一个独立的插件&#xff0c;或者其他任何独立的内容。把文章正文放在h…...

编程日记 2024/1/10 7:39:37

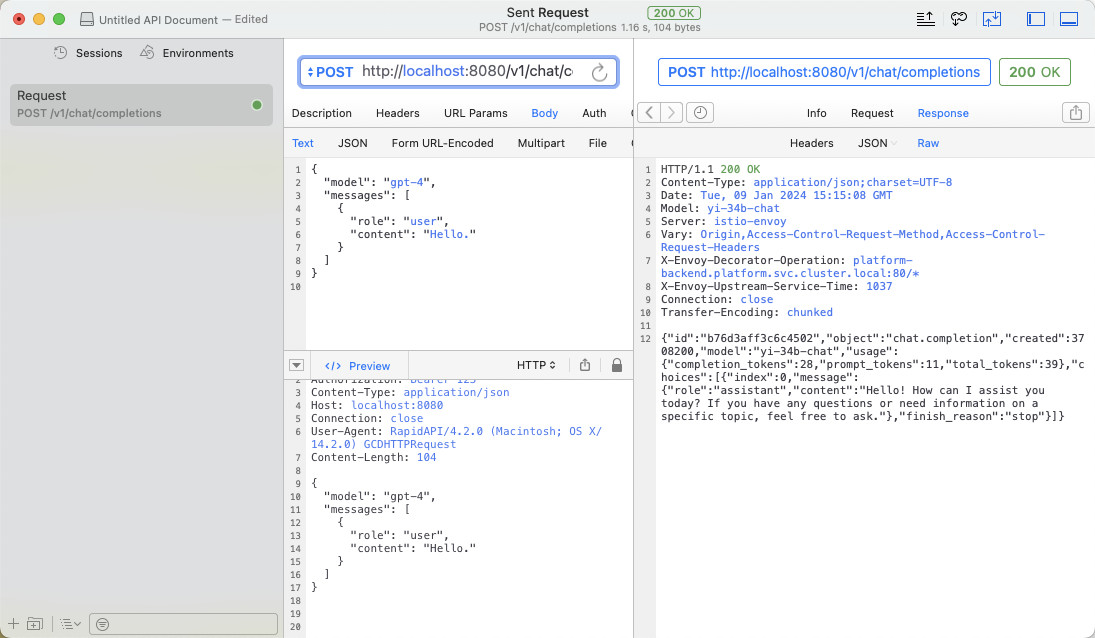
Amazing OpenAI API：把非 OpenAI 模型都按 OpenAI API 调用

分享一个有趣的小工具&#xff0c;10MB 身材的小工具&#xff0c;能够将各种不同的模型 API 转换为开箱即用的 OpenAI API 格式。 让许多依赖 OpenAI API 的软件能够借助开发者能够接触到的&#xff0c;非 OpenAI 的 API 私有部署和使用起来。 写在前面 这个小工具软件写于两…...

编程日记 2024/1/10 7:38:36

RK3568平台开发系列讲解（驱动篇）pinctrl 函数操作集结构体讲解

🚀返回专栏总目录 文章目录 一、pinctrl_ops二、pinmux_ops三、pinconf_ops沉淀、分享、成长，让自己和他人都能有所收获！😄 pinctrl_ops：提供有关属于引脚组的引脚的信息。pinmux_ops：选择连接到该引脚的功能。pinconf_ops：设置引脚属性（上拉，下拉，开漏，强度等）。…...

编程日记 2024/1/10 7:37:35

vue购物车案例，v-model 之 lazy、number、trim，与后端交互

购物车案例 <!DOCTYPE html> <html lang"en"> <head><meta charset"UTF-8"><title>Title</title><script src"./js/vue.js"></script> </head> <body> <div id"d1"&…...

编程日记 2024/1/10 7:33:32

云原生Kubernetes: Kubeadm部署K8S 1.29版本 单Master架构

目录 一、实验 1.环境 2.K8S master节点环境准备 3.K8S master节点安装kubelet、kubeadm、kubectl 3.K8S node节点环境准备与软件安装 4.K8S master节点部署服务 5.K8S node节点部署 6.K8S master节点查看集群 7.容器网络&#xff08;CNI&#xff09;部署 8.K8S 集群…...

编程日记 2024/1/10 7:32:31

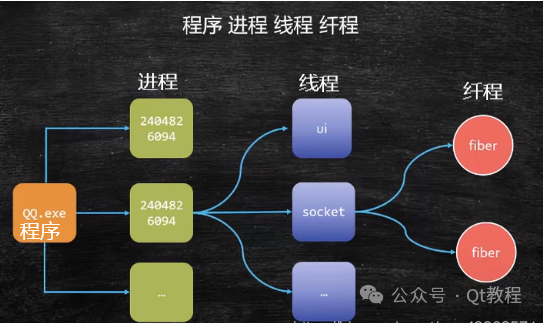
C++协程操作

什么是C++协程 C++中的协程是一种用户态轻量级线程，它拥有自己的上下文和栈，并且协程的切换和调度由用户定义，不需要陷入内核。如同一个进程可以拥有多个线程，一个线程也可以拥有多个协程。协程的优点在于极高的执行效率，因为协程切换不需要陷入内核，而是由用户程序定义切…...

编程日记 2024/1/10 7:30:30

计算机配件杂谈-鼠标

目录 基础知识鼠标的发展鼠标的左右手鼠标的显示样式鼠标的移动和可见性移动可见性 现在的我们的生活工作都基本上离不开电脑了&#xff0c;不管是你平时玩玩游戏&#xff0c;上班工作等等&#xff1b; 今天将关于鼠标的一些小的技巧分享出来&#xff0c;共勉&#xff01; 基础…...

编程日记 2024/1/10 7:29:29

用Python来制作一个微信聊天机器人

1. 效果展示 通过本地搭建一个flask服务器来接收信息&#xff0c;这里我简单使用展示&#xff0c;就没有对接收的信息进行处理了。 信息接收展示 发送信息展示 这里就直接使用python发送一个post请求即可&#xff0c;可以发送文字或者图片 代码展示 接收信息 #!/usr/bin/e…...

编程日记 2024/1/10 7:28:28

2024年第九届机器学习技术国际会议(ICMLT 2024) 即将召开

2024年第九届机器学习技术国际会议&#xff08;ICMLT 2024&#xff09;将于2024年5月24-26日在挪威奥斯陆举行。ICMLT 2024旨在讨论机器学习技术领域的最新研究技术现状和前沿趋势&#xff0c;为来自世界各地的科学家、工程师、实业家、学者和其他专业人士提供一个互动和交流的…...

编程日记 2024/1/10 7:27:27

算法训练day9Leetcode232用栈实现队列225用队列实现栈

今天学习的文章和视频链接 https://programmercarl.com/%E6%A0%88%E4%B8%8E%E9%98%9F%E5%88%97%E7%90%86%E8%AE%BA%E5%9F%BA%E7%A1%80.html 栈与队列理论基础 见我的博客 https://blog.csdn.net/qq_36372352/article/details/135470438?spm1001.2014.3001.5501 232用栈实现…...

编程日记 2024/1/10 7:26:26

Vue2 第一节_Vue2上手_插值表达式{{}}_访问数据和修改数据_Vue开发者工具

文章目录 1.Vue2上手-如何创建一个Vue实例,进行初始化渲染2. 插值表达式{{}}3. 访问数据和修改数据4. vue响应式5. Vue开发者工具--方便调试 1.Vue2上手-如何创建一个Vue实例,进行初始化渲染 准备容器引包创建Vue实例 new Vue()指定配置项 ->渲染数据 准备一个容器,例如: …...

编程新知 2025/12/15 20:41:51

OkHttp 中实现断点续传 demo

在 OkHttp 中实现断点续传主要通过以下步骤完成&#xff0c;核心是利用 HTTP 协议的 Range 请求头指定下载范围&#xff1a; 实现原理 Range 请求头&#xff1a;向服务器请求文件的特定字节范围&#xff08;如 Range: bytes1024-&#xff09; 本地文件记录&#xff1a;保存已…...

编程新知 2025/12/12 0:56:22

CocosCreator 之 JavaScript/TypeScript和Java的相互交互

引擎版本&#xff1a; 3.8.1 语言&#xff1a; JavaScript/TypeScript、C、Java 环境&#xff1a;Window 参考&#xff1a;Java原生反射机制 您好&#xff0c;我是鹤九日&#xff01; 回顾 在上篇文章中&#xff1a;CocosCreator Android项目接入UnityAds 广告SDK。 我们简单讲…...

编程新知 2025/12/14 12:44:16

DBAPI如何优雅的获取单条数据

API如何优雅的获取单条数据 案例一 对于查询类API&#xff0c;查询的是单条数据&#xff0c;比如根据主键ID查询用户信息&#xff0c;sql如下&#xff1a; select id, name, age from user where id #{id}API默认返回的数据格式是多条的&#xff0c;如下&#xff1a; {&qu…...

编程新知 2025/12/16 5:19:07

大语言模型（LLM）中的KV缓存压缩与动态稀疏注意力机制设计

随着大语言模型&#xff08;LLM&#xff09;参数规模的增长&#xff0c;推理阶段的内存占用和计算复杂度成为核心挑战。传统注意力机制的计算复杂度随序列长度呈二次方增长&#xff0c;而KV缓存的内存消耗可能高达数十GB&#xff08;例如Llama2-7B处理100K token时需50GB内存&a…...

编程新知 2025/11/27 23:47:29

docker 部署发现spring.profiles.active 问题

报错&#xff1a; org.springframework.boot.context.config.InvalidConfigDataPropertyException: Property spring.profiles.active imported from location class path resource [application-test.yml] is invalid in a profile specific resource [origin: class path re…...

编程新知 2025/9/20 12:14:18

MySQL JOIN 表过多的优化思路

当 MySQL 查询涉及大量表 JOIN 时&#xff0c;性能会显著下降。以下是优化思路和简易实现方法&#xff1a; 一、核心优化思路 减少 JOIN 数量 数据冗余&#xff1a;添加必要的冗余字段&#xff08;如订单表直接存储用户名&#xff09;合并表&#xff1a;将频繁关联的小表合并成…...

编程新知 2025/10/17 22:08:13

LabVIEW双光子成像系统技术

双光子成像技术的核心特性 双光子成像通过双低能量光子协同激发机制&#xff0c;展现出显著的技术优势&#xff1a; 深层组织穿透能力&#xff1a;适用于活体组织深度成像 高分辨率观测性能&#xff1a;满足微观结构的精细研究需求 低光毒性特点&#xff1a;减少对样本的损伤…...

编程新知 2025/12/1 2:54:46

libfmt: 现代C++的格式化工具库介绍与酷炫功能

libfmt: 现代C的格式化工具库介绍与酷炫功能 libfmt 是一个开源的C格式化库&#xff0c;提供了高效、安全的文本格式化功能&#xff0c;是C20中引入的std::format的基础实现。它比传统的printf和iostream更安全、更灵活、性能更好。 基本介绍 主要特点 类型安全&#xff1a…...

编程新知 2025/9/14 12:09:11

Sklearn 机器学习 缺失值处理 获取填充失值的统计值

💖亲爱的技术爱好者们，热烈欢迎来到 Kant2048 的博客！我是 Thomas Kant，很开心能在CSDN上与你们相遇～💖 本博客的精华专栏： 【自动化测试】 【测试经验】 【人工智能】 【Python】 使用 Scikit-learn 处理缺失值并提取填充统计信息的完整指南 在机器学习项目中，数据清…...

编程新知 2025/12/13 18:43:47