c# windows10大小端试
测试代码:
unsafe public void ceshi()
{byte[] by = BitConverter.GetBytes(0x12345678);Debug.WriteLine(" byte[0] = 0x" + by[0].ToString("x2"));Debug.WriteLine(" byte[1] = 0x" + by[1].ToString("x2"));Debug.WriteLine(" byte[2] = 0x" + by[2].ToString("x2"));Debug.WriteLine(" byte[3] = 0x" + by[3].ToString("x2"));for( int i = 0; i < 4;i ++){fixed (byte* pB = &by[i]){ulong addr = (ulong)pB; // 得到内存的地址Debug.WriteLine($" byte[{i}]地址 = 0x" + addr.ToString("x2"));}}
}输出结果
byte[0] = 0x78
byte[1] = 0x56
byte[2] = 0x34
byte[3] = 0x12
byte[0]地址 = 0x29a7af0
byte[1]地址 = 0x29a7af1
byte[2]地址 = 0x29a7af2
byte[3]地址 = 0x29a7af3
结论:
0 = 低字节
3 = 高字节
参考链接
单片机大小端模式-CSDN博客![]() https://blog.csdn.net/anlog/article/details/135338624
https://blog.csdn.net/anlog/article/details/135338624
特此记录
anlog
2024年1月5日
相关文章:
c# windows10大小端试
测试代码: unsafe public void ceshi() {byte[] by BitConverter.GetBytes(0x12345678);Debug.WriteLine(" byte[0] 0x" by[0].ToString("x2"));Debug.WriteLine(" byte[1] 0x" by[1].ToString("x2"));Debug.WriteLi…...

【算法专题】动态规划之斐波那契数列模型
动态规划1.0 动态规划 - - - 斐波那契数列模型1. 第 N 个泰波那契数2. 三步问题3. 使用最小花费爬楼梯4. 解码方法 动态规划 - - - 斐波那契数列模型 1. 第 N 个泰波那契数 题目链接 -> Leetcode -1137. 第 N 个泰波那契数 Leetcode -1137. 第 N 个泰波那契数 题目&…...
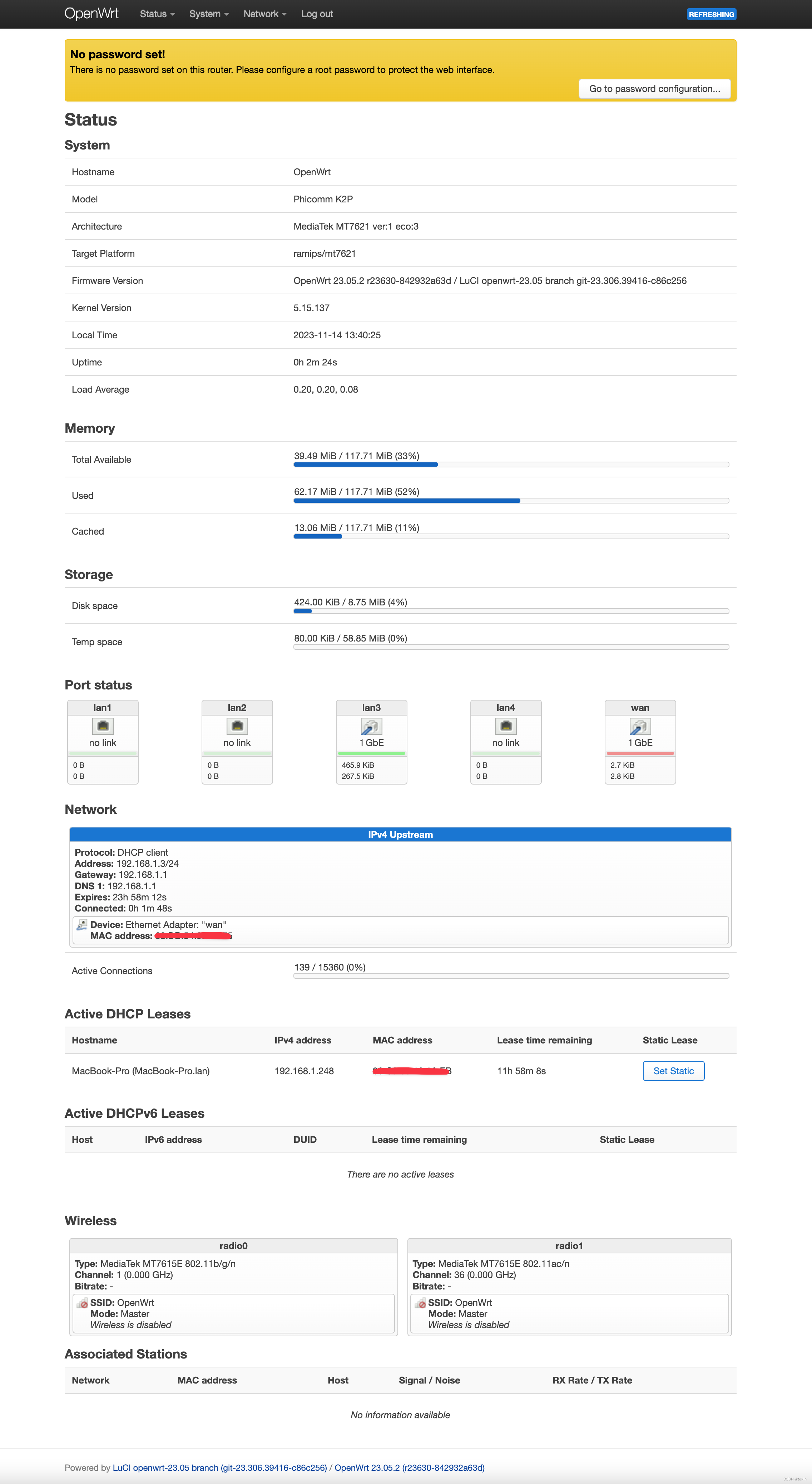
K2P路由器刷OpenWrt官方最新版本固件OpenWrt 23.05.2方法 其他型号的智能路由器OpenWrt固件刷入方法也基本上适用
最近路由器在开机时总出问题,于是就那他来开刀,直接刷一个OpenWrt官方最新版本的固件, 刷其他第三方的固件总是觉得不安全, 而且很多第三方固件都带了些小工具,始终会有安全隐患, 而且占用内存空间太多,本来这个东西就没有多少内存,于是就干脆刷一个官方的原始固件(才6.3M, 相…...

AI大语言模型会带来了新一波人工智能浪潮?
以ChatGPT、LLaMA、Gemini、DALLE、Midjourney、Stable Diffusion、星火大模型、文心一言、千问为代表AI大语言模型带来了新一波人工智能浪潮,可以面向科研选题、思维导图、数据清洗、统计分析、高级编程、代码调试、算法学习、论文检索、写作、翻译、润色、文献辅助…...

How to view the high-tech zone atmospheric project
How to view the high-tech zone atmospheric project 问题与建议登录界面没有验证码部分页面加载时间过长联动型下拉列表框点击反应迟钝页面缺乏导航没有采用https协议没有完成域名实名认证左侧菜单区不能收缩大屏区域功能图层不能完全隐藏部分页面表单控件没有文案提示其功能…...

sqlalchemy 中的缓存机制解释
SQLAlchemy 的缓存机制主要涉及两个层面:会话(Session)缓存和查询缓存。这两种缓存机制对于提升应用性能和数据一致性都非常重要。下面详细解释这两种缓存机制: 1. 会话(Session)缓存 会话缓存是 SQLAlch…...
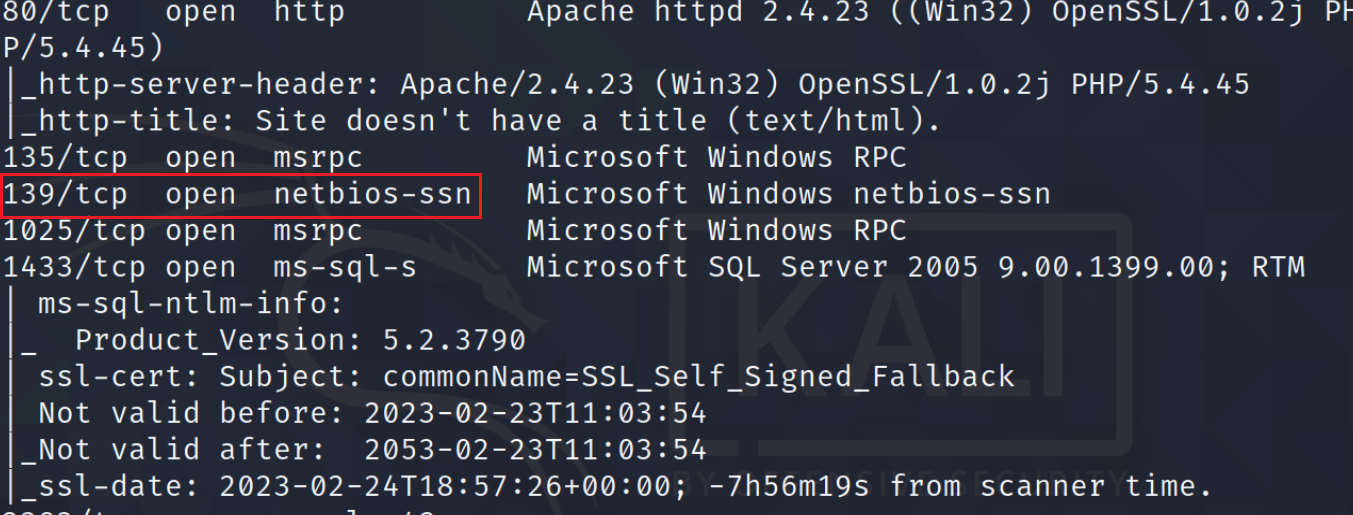
网络安全B模块(笔记详解)- 漏洞扫描与利用
漏洞扫描与利用 1.通过Kali对服务器场景server2003以半开放式不进行ping的扫描方式并配合a,要求扫描信息输出格式为xml文件格式,从生成扫描结果获取局域网(例如172.16.101.0/24)中存活靶机,以xml格式向指定文件输出信息(使用工具Nmap,使用必须要使用的参数),并将该操…...
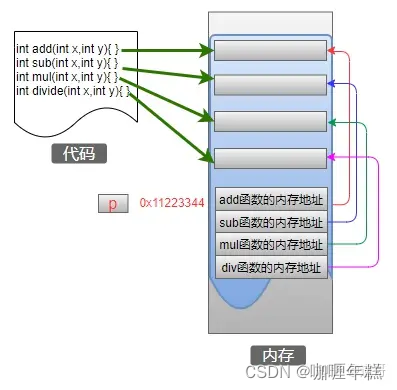
【C语言】指针——从底层原理到应用
C语言指针-从底层原理到花式技巧,用图文和代码帮你讲解透彻 目录 一、前言二、变量与指针的本质 1. 内存地址2. 32位与64位系统3. 变量4. 指针变量5. 操作指针变量 5.1 指针变量自身的值5.2 获取指针变量所指向的数据5.3 以什么样的数据类型来使用/解释指针变量所指…...

想了解步进伺服的朋友可以了解下这个方案
TMC4361A 是一款小型化、高性能的驱动步进电机的运动控制器。实用于很多的斜坡轮廓的应用,特别是速度快、限制过冲的运动场合。用户根据自己的要求实现 S 形或 sixPoint™六点式速度轮廓配置及闭环或开环的操作、动态修改运动参数。TMC4361A 包含 SPI接口、Step/Dir…...

航天航空线束工艺3D虚拟展馆支持多人异地参观漫游
为了满足汽车线束企业员工工作需要,让新老员工了解到更先进、规范的线束工艺设计技术,华锐视点基于VR虚拟仿真、web3d开发和图形图像技术制作了一款汽车线束工艺设计VR虚拟仿真模拟展示系统。 汽车线束工艺设计VR虚拟仿真模拟展示系统共分为pc电脑端和VR…...
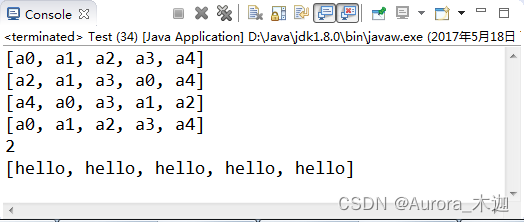
JAVA面向对象基础-容器
一、泛型 我们可以在类的声明处增加泛型列表,如:<T,E,V>。 此处,字符可以是任何标识符,一般采用这3个字母。 【示例9-1】泛型类的声明 1 2 3 4 5 6 7 8 9 10 class MyCollection<E> {// E:表示泛型; Object[] o…...

2022年山东省职业院校技能大赛高职组信息安全管理与评估—开发测试服务器解析
任务5:开发测试服务器 目录 任务5:开发测试服务器 解题方法:...

2024年我国网络安全发展形势展望
2023年,我国网络安全政策法规陆续出台,网络安全与数据安全产业发展势头强劲,网络安全形势整体向好。展望2024年,世界各国在网络空间中的竞争将变得愈发激烈,我国网络安全领域的法律法规将不断完善,数据安全…...
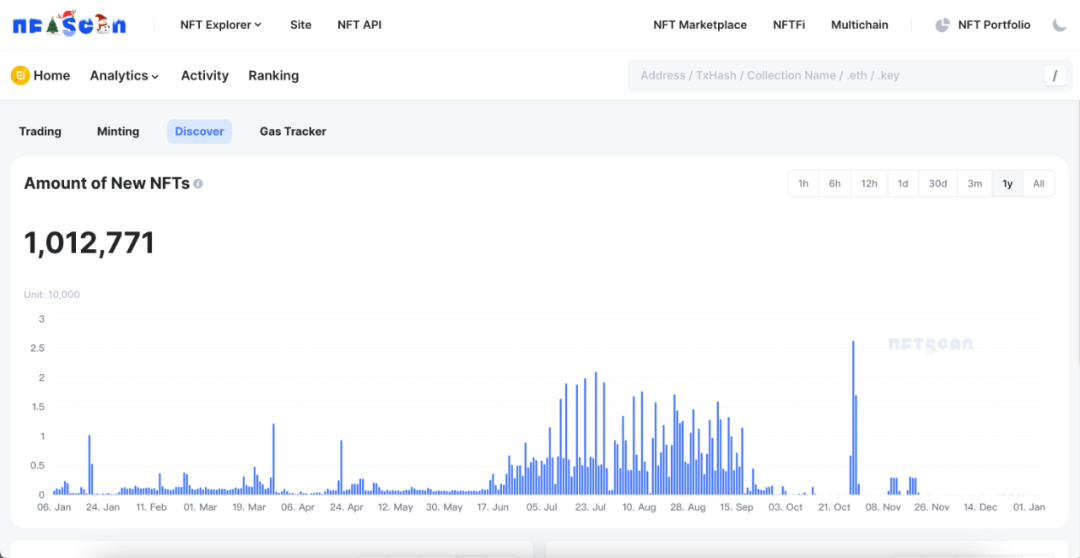
如何使用 NFTScan NFT API 在 PlatON 网络上开发 Web3 应用
PlatON 是由万向区块链和矩阵元主导开发的面向下一代的全球计算架构,创新性的采用元计算框架 Monad 和基于 Reload 覆盖网络的同构多链架构,其愿景是成为全球首个提供完备隐私保护能力的运营服务网络。它提供计算、存储、通讯服务,并提供算力…...
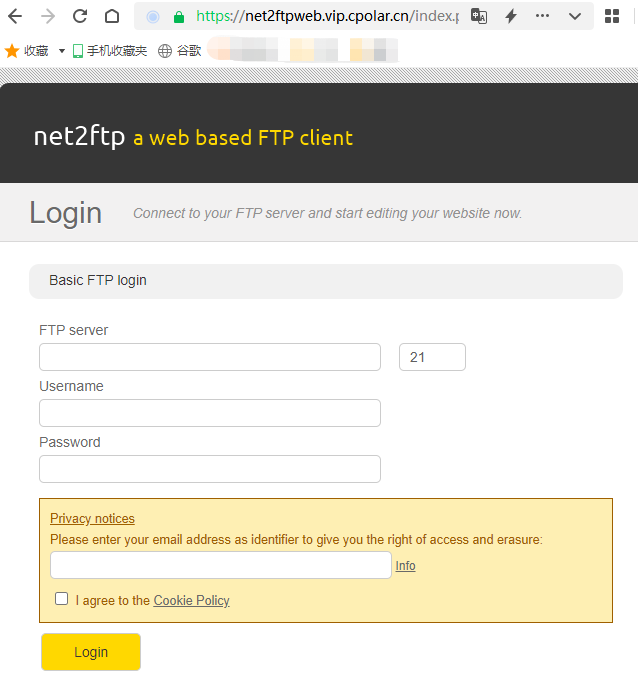
如何使用web文件管理器Net2FTP搭建个人网盘
文章目录 1.前言2. Net2FTP网站搭建2.1. Net2FTP下载和安装2.2. Net2FTP网页测试 3. cpolar内网穿透3.1.Cpolar云端设置3.2.Cpolar本地设置 4.公网访问测试5.结语 1.前言 文件传输可以说是互联网最主要的应用之一,特别是智能设备的大面积使用,无论是个人…...

总结多线程的各种锁
1、公平锁和非公平锁 公平锁是严格按照线程请求的顺序来分配锁,每一个线程都能获取到锁,避免线程饥饿现象;相反,非公平锁表示线程竞争锁时可以插队来抢占资源。 非公平锁在大多数情况下效率优于公平锁,因为公平锁涉及到…...

树形结构的窗口小部件
这段代码是一个使用Qt框架的C程序,实现了一个树形结构的窗口小部件(TreeWidget)。以下是主要的解释: #include "treewidget.h" #include "ui_treewidget.h"TreeWidget::TreeWidget(QWidget *parent) : QWidg…...

【现代密码学】笔记3.1-3.3 --规约证明、伪随机性《introduction to modern cryphtography》
【现代密码学】笔记3.1-3.3 --规约证明、伪随机性《introduction to modern cryphtography》 写在最前面私钥加密与伪随机性 第一部分密码学的计算方法论计算安全加密的定义:对称加密算法 伪随机性伪随机生成器(PRG) 规约法规约证明 构造安全…...
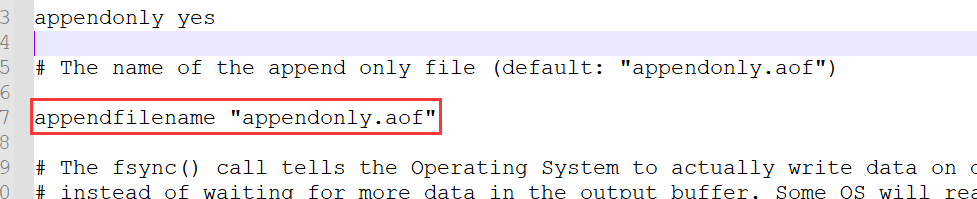
Redis底层原理
持久化 Redis虽然是个内存数据库,但是Redis支持RDB和AOF两种持久化机制,将数据写往磁盘,可以有效地避免因进程退出造成的数据丢失问题,当下次重启时利用之前持久化的文件即可实现数据恢复。 RDB RDB持久化是把当前进程数据生成快照保存到硬盘的过程。所谓内存快照,就是…...

掌握亚马逊、Lazada、shopee、速卖通、eBay、wish测评自养号补单系统:解锁跨境电商新机遇
在选择测评环境系统时,市面上有很多选项。但是,究竟哪个系统使用起来更高效、成本更低、成功率更高呢?下面将详细分析各种网络环境的使用经验,希望能帮助大家避免一些不必要的困扰和错误。我曾经亲自尝试过各种网络环境࿰…...

零门槛NAS搭建:WinNAS如何让普通电脑秒变私有云?
一、核心优势:专为Windows用户设计的极简NAS WinNAS由深圳耘想存储科技开发,是一款收费低廉但功能全面的Windows NAS工具,主打“无学习成本部署” 。与其他NAS软件相比,其优势在于: 无需硬件改造:将任意W…...

ubuntu搭建nfs服务centos挂载访问
在Ubuntu上设置NFS服务器 在Ubuntu上,你可以使用apt包管理器来安装NFS服务器。打开终端并运行: sudo apt update sudo apt install nfs-kernel-server创建共享目录 创建一个目录用于共享,例如/shared: sudo mkdir /shared sud…...

2025年能源电力系统与流体力学国际会议 (EPSFD 2025)
2025年能源电力系统与流体力学国际会议(EPSFD 2025)将于本年度在美丽的杭州盛大召开。作为全球能源、电力系统以及流体力学领域的顶级盛会,EPSFD 2025旨在为来自世界各地的科学家、工程师和研究人员提供一个展示最新研究成果、分享实践经验及…...

学习STC51单片机31(芯片为STC89C52RCRC)OLED显示屏1
每日一言 生活的美好,总是藏在那些你咬牙坚持的日子里。 硬件:OLED 以后要用到OLED的时候找到这个文件 OLED的设备地址 SSD1306"SSD" 是品牌缩写,"1306" 是产品编号。 驱动 OLED 屏幕的 IIC 总线数据传输格式 示意图 …...

鸿蒙DevEco Studio HarmonyOS 5跑酷小游戏实现指南
1. 项目概述 本跑酷小游戏基于鸿蒙HarmonyOS 5开发,使用DevEco Studio作为开发工具,采用Java语言实现,包含角色控制、障碍物生成和分数计算系统。 2. 项目结构 /src/main/java/com/example/runner/├── MainAbilitySlice.java // 主界…...
相比,优缺点是什么?适用于哪些场景?)
Redis的发布订阅模式与专业的 MQ(如 Kafka, RabbitMQ)相比,优缺点是什么?适用于哪些场景?
Redis 的发布订阅(Pub/Sub)模式与专业的 MQ(Message Queue)如 Kafka、RabbitMQ 进行比较,核心的权衡点在于:简单与速度 vs. 可靠与功能。 下面我们详细展开对比。 Redis Pub/Sub 的核心特点 它是一个发后…...

安全突围:重塑内生安全体系:齐向东在2025年BCS大会的演讲
文章目录 前言第一部分:体系力量是突围之钥第一重困境是体系思想落地不畅。第二重困境是大小体系融合瓶颈。第三重困境是“小体系”运营梗阻。 第二部分:体系矛盾是突围之障一是数据孤岛的障碍。二是投入不足的障碍。三是新旧兼容难的障碍。 第三部分&am…...

WebRTC从入门到实践 - 零基础教程
WebRTC从入门到实践 - 零基础教程 目录 WebRTC简介 基础概念 工作原理 开发环境搭建 基础实践 三个实战案例 常见问题解答 1. WebRTC简介 1.1 什么是WebRTC? WebRTC(Web Real-Time Communication)是一个支持网页浏览器进行实时语音…...

深入理解Optional:处理空指针异常
1. 使用Optional处理可能为空的集合 在Java开发中,集合判空是一个常见但容易出错的场景。传统方式虽然可行,但存在一些潜在问题: // 传统判空方式 if (!CollectionUtils.isEmpty(userInfoList)) {for (UserInfo userInfo : userInfoList) {…...

用神经网络读懂你的“心情”:揭秘情绪识别系统背后的AI魔法
用神经网络读懂你的“心情”:揭秘情绪识别系统背后的AI魔法 大家好,我是Echo_Wish。最近刷短视频、看直播,有没有发现,越来越多的应用都开始“懂你”了——它们能感知你的情绪,推荐更合适的内容,甚至帮客服识别用户情绪,提升服务体验。这背后,神经网络在悄悄发力,撑起…...
