LeetCode 2807. 在链表中插入最大公约数【链表,迭代,递归】1279
本文属于「征服LeetCode」系列文章之一,这一系列正式开始于2021/08/12。由于LeetCode上部分题目有锁,本系列将至少持续到刷完所有无锁题之日为止;由于LeetCode还在不断地创建新题,本系列的终止日期可能是永远。在这一系列刷题文章中,我不仅会讲解多种解题思路及其优化,还会用多种编程语言实现题解,涉及到通用解法时更将归纳总结出相应的算法模板。
为了方便在PC上运行调试、分享代码文件,我还建立了相关的仓库:https://github.com/memcpy0/LeetCode-Conquest。在这一仓库中,你不仅可以看到LeetCode原题链接、题解代码、题解文章链接、同类题目归纳、通用解法总结等,还可以看到原题出现频率和相关企业等重要信息。如果有其他优选题解,还可以一同分享给他人。
由于本系列文章的内容随时可能发生更新变动,欢迎关注和收藏征服LeetCode系列文章目录一文以作备忘。
给你一个链表的头 head ,每个结点包含一个整数值。
在相邻结点之间,请你插入一个新的结点,结点值为这两个相邻结点值的 最大公约数 。
请你返回插入之后的链表。
两个数的 最大公约数 是可以被两个数字整除的最大正整数。
示例 1:
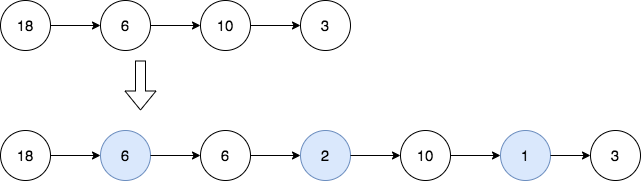
输入:head = [18,6,10,3]
输出:[18,6,6,2,10,1,3]
解释:第一幅图是一开始的链表,第二幅图是插入新结点后的图(蓝色结点为新插入结点)。
- 18 和 6 的最大公约数为 6 ,插入第一和第二个结点之间。
- 6 和 10 的最大公约数为 2 ,插入第二和第三个结点之间。
- 10 和 3 的最大公约数为 1 ,插入第三和第四个结点之间。
所有相邻结点之间都插入完毕,返回链表。
示例 2:
输入:head = [7]
输出:[7]
解释:第一幅图是一开始的链表,第二幅图是插入新结点后的图(蓝色结点为新插入结点)。
没有相邻结点,所以返回初始链表。
提示:
- 链表中结点数目在
[1, 5000]之间。 1 <= Node.val <= 1000
解法 迭代
遍历链表,在当前节点 cur \textit{cur} cur 后面插入 g c d gcd gcd 节点,同时 gcd \textit{gcd} gcd 节点指向 cur \textit{cur} cur 的下一个节点。插入后, cur \textit{cur} cur 更新为 cur . next . next \textit{cur}.\textit{next}.\textit{next} cur.next.next ,也就是 c u r cur cur 原来的下一个节点,开始下一轮循环。循环直到 c u r cur cur 没有下一个节点为止。
// cpp
class Solution {
public:ListNode* insertGreatestCommonDivisors(ListNode* head) {for (auto cur = head; cur->next; cur = cur->next->next)cur->next = new ListNode(gcd(cur->val, cur->next->val), cur->next);return head;}
};
// java
class Solution {public ListNode insertGreatestCommonDivisors(ListNode head) {for (ListNode cur = head; cur.next != null; cur = cur.next.next) {cur.next = new ListNode(gcd(cur.val, cur.next.val), cur.next);}return head;}private int gcd(int a, int b) { while (a != 0) {int t = a;a = b % a;b = t;}return b;}
}
// python
class Solution:def insertGreatestCommonDivisors(self, head: Optional[ListNode]) -> Optional[ListNode]:cur = headwhile cur.next:cur.next = ListNode(gcd(cur.val, cur.next.val), cur.next)cur = cur.next.nextreturn head
// go
/*** Definition for singly-linked list.* type ListNode struct {* Val int* Next *ListNode* }*/
func insertGreatestCommonDivisors(head *ListNode) *ListNode {for cur := head; cur.Next != nil; cur = cur.Next.Next {cur.Next = &ListNode{gcd(cur.Val, cur.Next.Val), cur.Next}}return head
}
func gcd(a, b int) int {for a != 0 {a, b = b % a, a}return b
}
// rust
// Definition for singly-linked list.
// #[derive(PartialEq, Eq, Clone, Debug)]
// pub struct ListNode {
// pub val: i32,
// pub next: Option<Box<ListNode>>
// }
//
// impl ListNode {
// #[inline]
// fn new(val: i32) -> Self {
// ListNode {
// next: None,
// val
// }
// }
// }
impl Solution {pub fn insert_greatest_common_divisors(mut head: Option<Box<ListNode>>) -> Option<Box<ListNode>> {let mut cur = &mut head;while cur.as_ref().unwrap().next.is_some() {let x = cur.as_mut().unwrap();let next = x.next.take();x.next = Some(Box::new(ListNode {val: Self::gcd(x.val, next.as_ref().unwrap().val),next,}));cur = &mut cur.as_mut().unwrap().next.as_mut().unwrap().next;}head}fn gcd(mut a: i32, mut b: i32) -> i32 {while a != 0 {(a, b) = (b % a, a);}b}
}
复杂度分析:
- 时间复杂度: O ( n log U ) \mathcal{O}(n\logU) O(nlogU) ,其中 n n n 为链表长度, U U U 为节点值的最大值。每次计算 g c d gcd gcd 需要 O ( log U ) \mathcal{O}(\logU) O(logU) 的时间。
- 空间复杂度: O ( 1 ) \mathcal{O}(1) O(1) 。返回值的空间不计入。
相关文章:

LeetCode 2807. 在链表中插入最大公约数【链表,迭代,递归】1279
本文属于「征服LeetCode」系列文章之一,这一系列正式开始于2021/08/12。由于LeetCode上部分题目有锁,本系列将至少持续到刷完所有无锁题之日为止;由于LeetCode还在不断地创建新题,本系列的终止日期可能是永远。在这一系列刷题文章…...

Hive之set参数大全-3
D 是否启用本地任务调试模式 hive.debug.localtask 是 Apache Hive 中的一个配置参数,用于控制是否启用本地任务调试模式。在调试模式下,Hive 将尝试在本地模式下运行一些任务,以便更容易调试和分析问题。 具体来说,当 hive.de…...
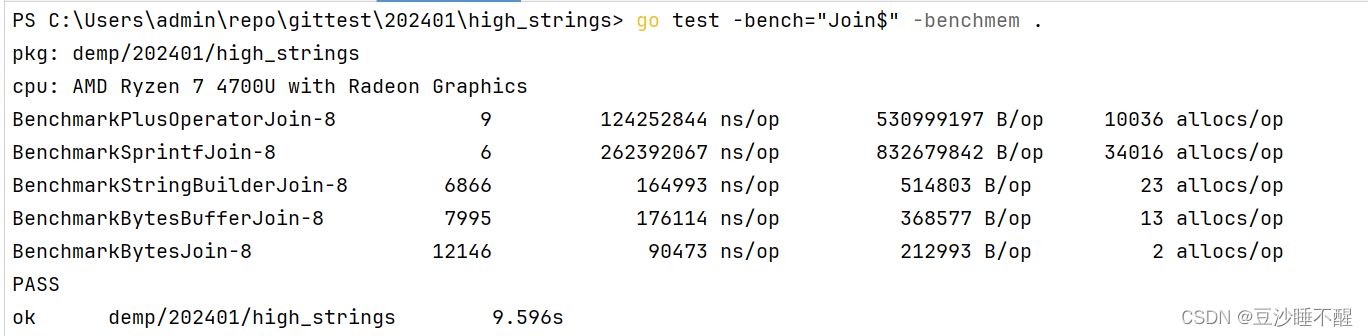
Golang拼接字符串性能对比
g o l a n g golang golang的 s t r i n g string string类型是不可修改的,对于拼接字符串来说,本质上还是创建一个新的对象将数据放进去。主要有以下几种拼接方式 拼接方式介绍 1.使用 s t r i n g string string自带的运算符 ans ans s2. 使用…...

【问题解决】web页面html锚点定位后内容被遮挡问题解决【暗锚】
正常的锚点跳转 a标签的href填写目标元素的id即可 <a href"#my_target">to div1</a> <div id"my_target">div1</div> 内容被顶栏遮挡示例 但是当id所在元素被嵌套多层flex和relative布局之后,跳转后部分内容会被遮挡…...

easyui datagrid无数据时显示无数据
这里写自定义目录标题 需求解决办法 需求 使用datagrid显示记录时,结果查询记录数为0,此时需要显示无数据。 示例代码 <table id"dg"></table>$(#dg).datagrid({url:datagrid_data.json,columns:[[{field:code,title:Code,widt…...

动态规划python简单例子-斐波那契数列
def fibonacci(n):dp [0, 1] [0] * (n - 1) # 初始化动态规划数组for i in range(2, n 1):dp[i] dp[i - 1] dp[i - 2] # 计算斐波那契数列的第 i 项print(dp)return dp[n] # 返回斐波那契数列的第 n 项# 示例用法 n 10 # 计算斐波那契数列的第 10 项 result fibonac…...
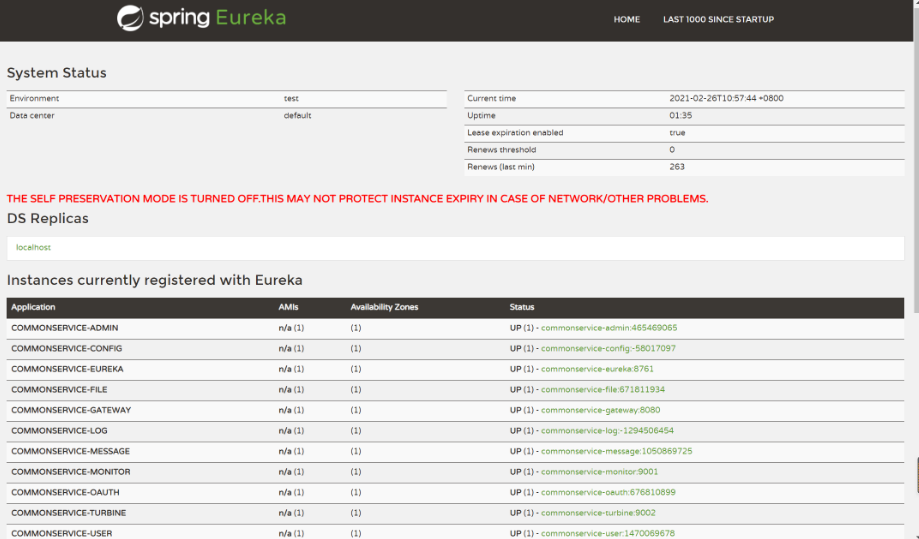
免 费 搭 建 多模式商城:b2b2c、o2o、直播带货一网打尽
鸿鹄云商 b2b2c产品概述 【b2b2c平台】,以传统电商行业为基石,鸿鹄云商支持“商家入驻平台自营”多运营模式,积极打造“全新市场,全新 模式”企业级b2b2c电商平台,致力干助力各行/互联网创业腾飞并获取更多的收益。从消…...

Python AttributeError: ‘NoneType‘ object has no attribute ‘shape‘如何解决
Python AttributeError: ‘NoneType‘ object has no attribute ‘shape‘ 运行出现上述错误,这个错误表示某个图像对象为 NoneType ,没有 shape 属性。通常情况下,这是因为 OpenCV 没有能够正确地加载图像,导致无法访问图像数据。…...
vue3自定义确认密码匹配验证规则
// 自定义确认密码匹配验证规则 const matchPassword (rules:any, value:any, callback:any) > {if (value ! addData.payPwd) {callback(new Error(两次密码输入不一致!))} else {callback()} }const rules reactive({payPwd: [{ required: true, message: &q…...

岗位所处定位,岗位职责
电子产品所需岗位:pcb设计电路板,fpga,嵌入式,应用层(前后端,移动端)。 PCB 岗位职责:1.负责器件.工程或者项目与技术验证类的PCB板设计工作;2.协助项目中部分模块的PCB(…...

2024阿里云服务器配置推荐方案
阿里云服务器配置怎么选择合适?CPU内存、公网带宽和ECS实例规格怎么选择合适?阿里云服务器网aliyunfuwuqi.com建议根据实际使用场景选择,例如企业网站后台、自建数据库、企业OA、ERP等办公系统、线下IDC直接映射、高性能计算和大游戏并发&…...

OceanBase原生分布式数据库
1.历史背景 在Java Web项目中,常常使用免费开源的MySQL数据库存储业务数据,按业界经验MySQL单库超过多大数据体量,或单表超过几百万条数据后就会出现查询变慢的情况,单实例数据库只能扩展物理资源(CPU、内存),来提升查…...

首次使用go-admin
go-admin 1.1 拉取 拉去后端代码 git clone https://github.com/go-admin-team/go-admin.git拉取前端代码 git clone gitgithub.com:go-admin-team/go-admin-ui.git 1.2 编译 cd ./go-admingo mod tidygo build1.3 配置文件的修改 这里可以可以根据自己的需要进行自定义两…...
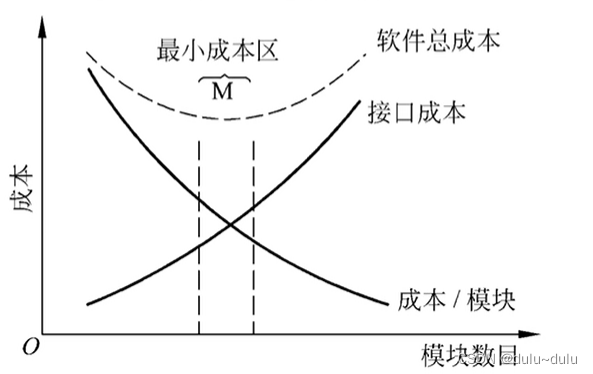
软件工程概论---内聚性和耦合性
目录 一.耦合性 1.内容耦合 2.公共耦合 4.控制耦合 5.标记耦合(特征耦合) 6.数据耦合 7.非直接耦合 二.内聚性 1.偶然内聚 2.逻辑内聚 3.时间内聚 4.过程内聚 5.通信内聚 6.顺序内聚 7.功能内聚 一.耦合性 耦合性是指软件结构中模块相互…...

纯血鸿蒙「扩圈」100天,酝酿已久的突围
坦白讲,去年参加华为开发者大会看到HarmonyOS NEXT(仅运行鸿蒙原生应用,所以也称作「纯血鸿蒙」)的时候,小雷也没料想到鸿蒙原生应用生态的发展速度会如此之快。 9月25日,华为正式对外宣布启动HarmonyOS NE…...
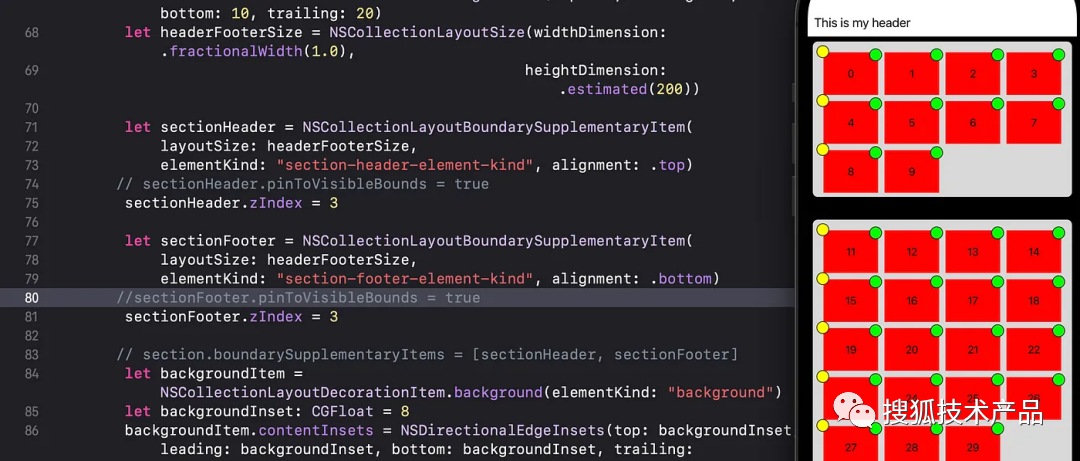
UICollection Compositional Layout全详解
本文字数:8325字 预计阅读时间:45分钟 01 Collection View Layout全详解 UICollectionView在iOS中是构建复杂布局的强大工具。iOS13中引入的 UICollectionViewCompositionalLayout为创建自定义布局提供了全新的可能性。本文将深入探讨Compositional Lay…...

单例模式的模板
参考了网上的一些单例模式,自己也写一个模板。 要点: 线程安全性单例对象的唯一性 #include <mutex> //在模板类 Singleton 中,可以定义单例模式的实现细节 template <typename T> class Singleton { public://通过删除拷贝构造…...

C#基础-空处理
在c#中,值对象是没有办法赋值为null的。比如说,你想要定义一个布尔值,你的赋值数据要么得是true、要么就得是false,默认情况下我们永远没可能给这个布尔赋值为null,即使只是对这个变量进行声明而不初始化数据ÿ…...

测试平台开发vue组件化重构前端代码
基于 springbootvue 的测试平台开发 继续更新(人在魔都 T_T)。 这期其实并不是一个详细的开发过程记录,主要还是针对本次前端重构来聊聊几个关注点。 目前重构的总进度在80%,重构完的页面没什么变化,再回顾一下。 一…...

龍运当头--html做一个中国火龙祝大家龙年大吉
🐉效果展示 🐉HTML展示 <body> <!-- partial:index.partial.html --> <svg><defs><g id=...

Ubuntu系统下交叉编译openssl
一、参考资料 OpenSSL&&libcurl库的交叉编译 - hesetone - 博客园 二、准备工作 1. 编译环境 宿主机:Ubuntu 20.04.6 LTSHost:ARM32位交叉编译器:arm-linux-gnueabihf-gcc-11.1.0 2. 设置交叉编译工具链 在交叉编译之前&#x…...

Linux链表操作全解析
Linux C语言链表深度解析与实战技巧 一、链表基础概念与内核链表优势1.1 为什么使用链表?1.2 Linux 内核链表与用户态链表的区别 二、内核链表结构与宏解析常用宏/函数 三、内核链表的优点四、用户态链表示例五、双向循环链表在内核中的实现优势5.1 插入效率5.2 安全…...

Debian系统简介
目录 Debian系统介绍 Debian版本介绍 Debian软件源介绍 软件包管理工具dpkg dpkg核心指令详解 安装软件包 卸载软件包 查询软件包状态 验证软件包完整性 手动处理依赖关系 dpkg vs apt Debian系统介绍 Debian 和 Ubuntu 都是基于 Debian内核 的 Linux 发行版ÿ…...

ArcGIS Pro制作水平横向图例+多级标注
今天介绍下载ArcGIS Pro中如何设置水平横向图例。 之前我们介绍了ArcGIS的横向图例制作:ArcGIS横向、多列图例、顺序重排、符号居中、批量更改图例符号等等(ArcGIS出图图例8大技巧),那这次我们看看ArcGIS Pro如何更加快捷的操作。…...

Xen Server服务器释放磁盘空间
disk.sh #!/bin/bashcd /run/sr-mount/e54f0646-ae11-0457-b64f-eba4673b824c # 全部虚拟机物理磁盘文件存储 a$(ls -l | awk {print $NF} | cut -d. -f1) # 使用中的虚拟机物理磁盘文件 b$(xe vm-disk-list --multiple | grep uuid | awk {print $NF})printf "%s\n"…...
安装docker)
Linux离线(zip方式)安装docker
目录 基础信息操作系统信息docker信息 安装实例安装步骤示例 遇到的问题问题1:修改默认工作路径启动失败问题2 找不到对应组 基础信息 操作系统信息 OS版本:CentOS 7 64位 内核版本:3.10.0 相关命令: uname -rcat /etc/os-rele…...

智能AI电话机器人系统的识别能力现状与发展水平
一、引言 随着人工智能技术的飞速发展,AI电话机器人系统已经从简单的自动应答工具演变为具备复杂交互能力的智能助手。这类系统结合了语音识别、自然语言处理、情感计算和机器学习等多项前沿技术,在客户服务、营销推广、信息查询等领域发挥着越来越重要…...

基于Springboot+Vue的办公管理系统
角色: 管理员、员工 技术: 后端: SpringBoot, Vue2, MySQL, Mybatis-Plus 前端: Vue2, Element-UI, Axios, Echarts, Vue-Router 核心功能: 该办公管理系统是一个综合性的企业内部管理平台,旨在提升企业运营效率和员工管理水…...

代码规范和架构【立芯理论一】(2025.06.08)
1、代码规范的目标 代码简洁精炼、美观,可持续性好高效率高复用,可移植性好高内聚,低耦合没有冗余规范性,代码有规可循,可以看出自己当时的思考过程特殊排版,特殊语法,特殊指令,必须…...

Python Einops库:深度学习中的张量操作革命
Einops(爱因斯坦操作库)就像给张量操作戴上了一副"语义眼镜"——让你用人类能理解的方式告诉计算机如何操作多维数组。这个基于爱因斯坦求和约定的库,用类似自然语言的表达式替代了晦涩的API调用,彻底改变了深度学习工程…...
