CentOS 6 制作openssh 9.6 p1 rpm包(含ssh-copy-id、openssl) —— 筑梦之路
openssh 9.6 需要openssl 1.1.1 以上版本，因此需要先安装openssl 1.1.1，可阅读这篇升级更新openssl版本到1.1.1w
CentOS 6 制作openssl 1.1.1w rpm包 —— 筑梦之路-CSDN博客
CentOS 6很久都停止更新和支持，关于此版本的写的不多，之前写过这篇可作为参考
CentOS 6 源码制作openssh8.9/9.0/9.1/9.2/9.3 p1 rpm包——筑梦之路_openssh rpm包下载-CSDN博客
openssh 9.6和之前的版本区别比较大，因此改了一些地方才能完成rpm二进制包的制作，可下载src源码包，这里就不再贴spec文件内容，相关的src源码包和二进制rpm包见我的资源。
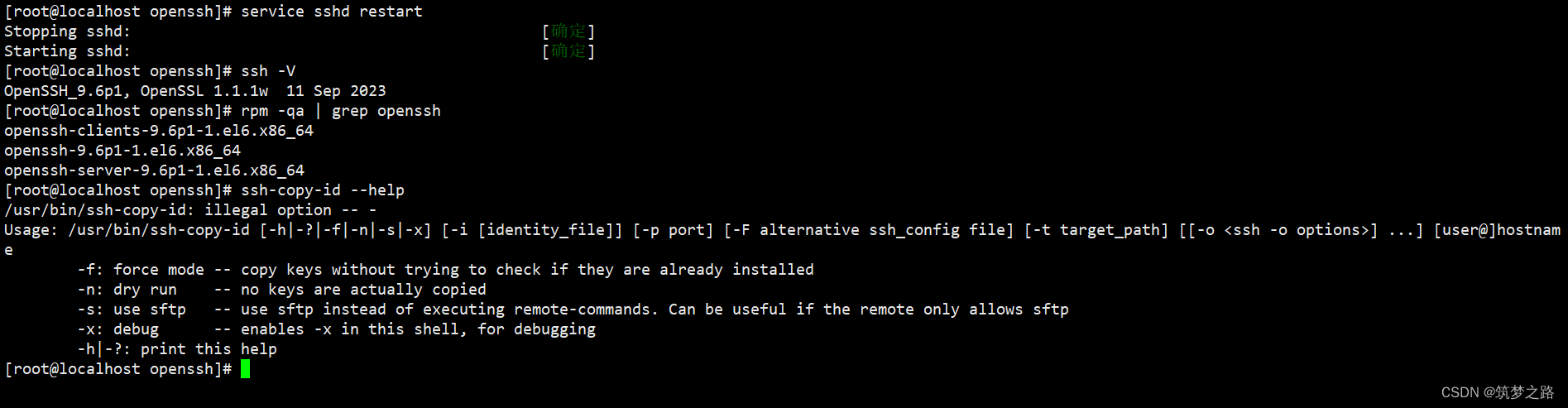
这里我主要添加了ssh-copy-id命令、显示openssl版本信息。
安装后效果如图：
相关文章：
CentOS 6 制作openssh 9.6 p1 rpm包(含ssh-copy-id、openssl) —— 筑梦之路
openssh 9.6 需要openssl 1.1.1 以上版本，因此需要先安装openssl 1.1.1，可阅读这篇升级更新openssl版本到1.1.1w CentOS 6 制作openssl 1.1.1w rpm包 —— 筑梦之路-CSDN博客 CentOS 6很久都停止更新和支持，关于此版本的写的不多ÿ…...
Tomcat Notes: Deployment File
This is a personal study notes of Apache Tomcat. Below are main reference material. - YouTube Apache Tomcat Full Tutorial，owed by Alpha Brains Courses. https://www.youtube.com/watch?vrElJIPRw5iM&t801s 1、Tomcat deployment1.1、Two modes of …...
某邦通信股份有限公司IP网络对讲广播系统挖矿检测脚本
目录 1.漏洞概述 2.影响版本 3.危害等级 4.挖矿程序检测 5.Nuclei自动化检测...
uniapp点击跳转传对象
目录 传对象传对象传送组件接受组件 最后 传对象 传对象 传送组件 点击传给组件 <view class"dki-tit-edit" click"gotificatedit(item)">编辑 </view>gotificatedit(item){console.log(item,item);let options JSON.stringify(item);uni.…...
简单用PHP实现微信小程序的游戏功能
微信小程序的兴起，越来越多的开发者开始关注如何在小程序中实现游戏功能。PHP作为一种流行的后端语言，可以很好地与小程序进行搭配，实现游戏功能。下面将介绍如何使用PHP来实现微信小程序的游戏功能，并提供具体的代码示例。 建立…...
某查查请求头参数加密分析（含JS加密算法与Python爬虫源码）
文章目录 1. 写在前面2. 请求分析3. 断点分析4. 扣加密JS5. Python爬虫代码实现 【作者主页】：吴秋霖 【作者介绍】：Python领域优质创作者、阿里云博客专家、华为云享专家。长期致力于Python与爬虫领域研究与开发工作！ 【作者推荐】ÿ…...
免费用chatGPT
免费用chatGPT，地址： DocGPT - 第二大脑...
还不会python 实现常用的数据编码和对称加密？看这篇文章就够啦~
相信很多使用 python 的小伙伴在工作中都遇到过，对数据进行相关编码或加密的需求，今天这篇文章主要给大家介绍对于一些常用的数据编码和数据加密的方式，如何使用 python 去实现。话不多说，接下来直接进入主题： 前言 1…...
简易实现 MyBatis 底层机制
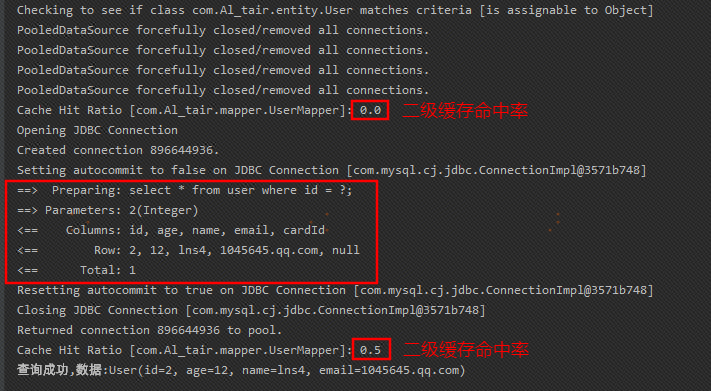
MyBatis 大家好呀！我是小笙，我中间有1年没有更新文章了，主要忙于毕业和就业相关事情，接下来，我会恢复更新！我们一起努力吧！ 概述 MyBatis 是一个持久层的框架（前身是 ibatis&#x…...
PhpPythonC++圆类的实现（OOP）
哎......被投诉了 😭😭😭😭😭 其实也不是小编不更，这不是期末了吗（zhaojiekou~~），而且最近学的信息收集和ctf感觉好像没找到啥能更的（不过最经还是在考虑更一…...
OpenSSL升级版本
1 查看openssl版本 $ openssl version OpenSSL 1.0.2k-fips 26 Jan 2017 目前是1.0版本系列. 2 下载最新稳定版本的OpenSSL源码包 $ wget https://www.openssl.org/source/openssl-1.1.1q.tar.gz 3 编译源码安装 tar -xzvf openssl-1.1.1q.tar.gz cd openssl-1.1.1q .…...
基于sprinmgboot实习管理系统源码和论文
随着信息化时代的到来，管理系统都趋向于智能化、系统化，实习管理也不例外，但目前国内仍都使用人工管理，市场规模越来越大，同时信息量也越来越庞大，人工管理显然已无法应对时代的变化，而实习管理…...
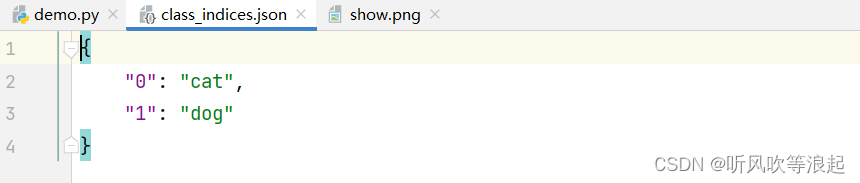
图像分类任务的可视化脚本，生成类别json字典文件
1. 前言 之前的图像分类任务可视化，都是在train脚本里， 用torch中dataloader将图片和类别加载，然后利用matplotlib库进行可视化。 如这篇文章中：CNN 卷积神经网络对染色血液细胞分类(blood-cells) 在分类任务中，必定…...
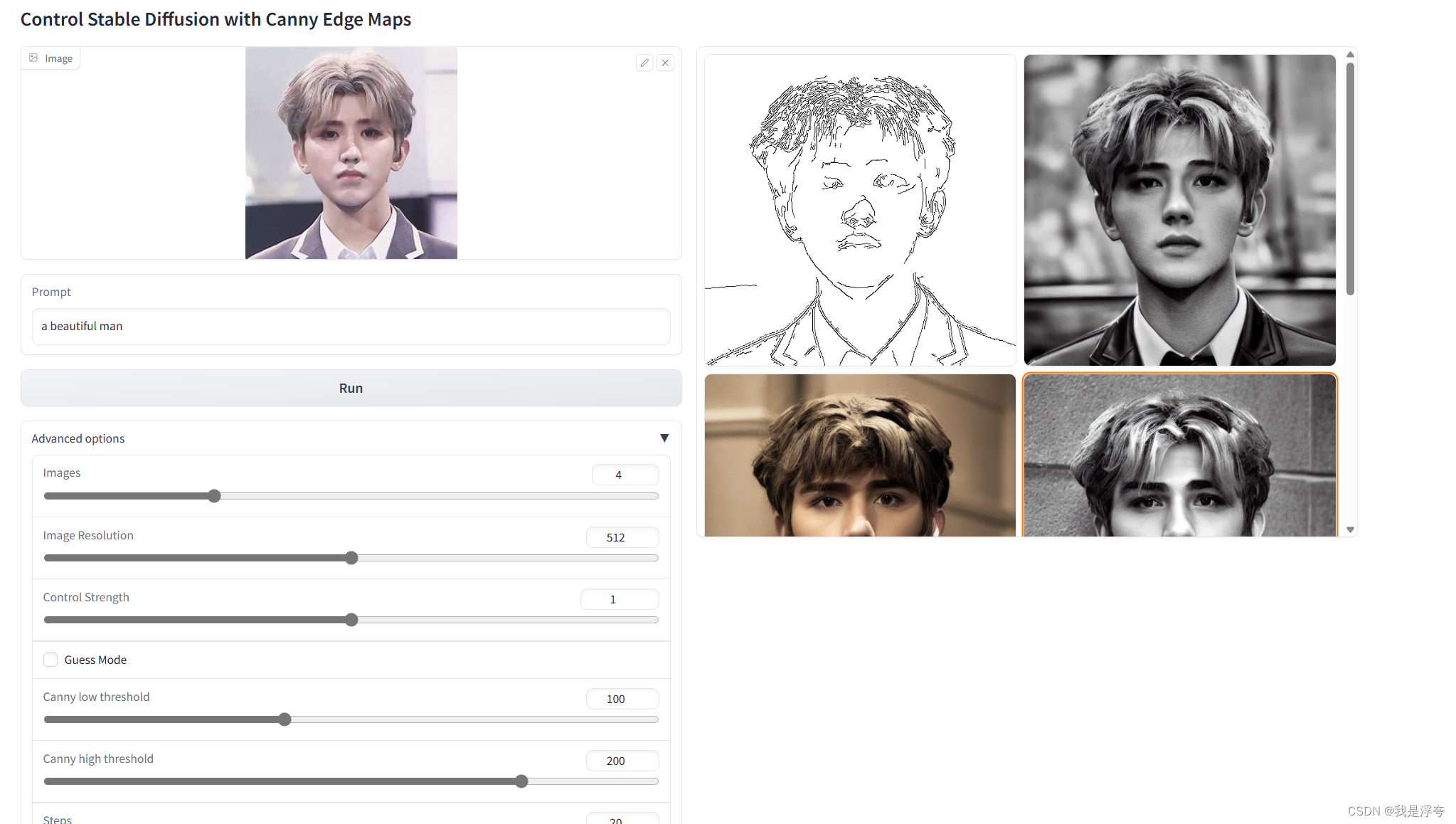
Adding Conditional Control to Text-to-Image Diffusion Models——【代码复现】
官方实现代码地址：lllyasviel/ControlNet: Let us control diffusion models! (github.com) 一、前言 此项目的使用需要显存大于8G，训练自己的ControlNet或需要更大，因此请注意查看自身硬件是否符合。 在此之前请确保已经安装好python以及…...
java-Exchanger详解
1.概述 java.util.concurrent.Exchanger。这在Java中作为两个线程之间交换对象的公共点。 2.Exchanger简介 Exchanger类可用于在两个类型为T的线程之间共享对象。该类仅提供了一个重载的方法exchange(T t)。 当调用exchanger时，它会等待成对的另一个线程也调用它…...
‘再战千问：启程你的提升之旅‘，如何更好地提问？
例如，很多时候我们提出一些问题，然而通义千问提供的答案，并非完全符合我们的期望。这并非由于通义千问的智能程度不足，而是提问者的“提问技巧”尚未掌握得当。 难道提问还需要讲究艺术性吗？确实如此。今天，…...
java SSM社区文化服务管理系统myeclipse开发mysql数据库springMVC模式java编程计算机网页设计
一、源码特点 java SSM社区文化服务管理系统是一套完善的web设计系统（系统采用SSM框架进行设计开发，springspringMVCmybatis），对理解JSP java编程开发语言有帮助，系统具有完整的 源代码和数据库，系统主…...
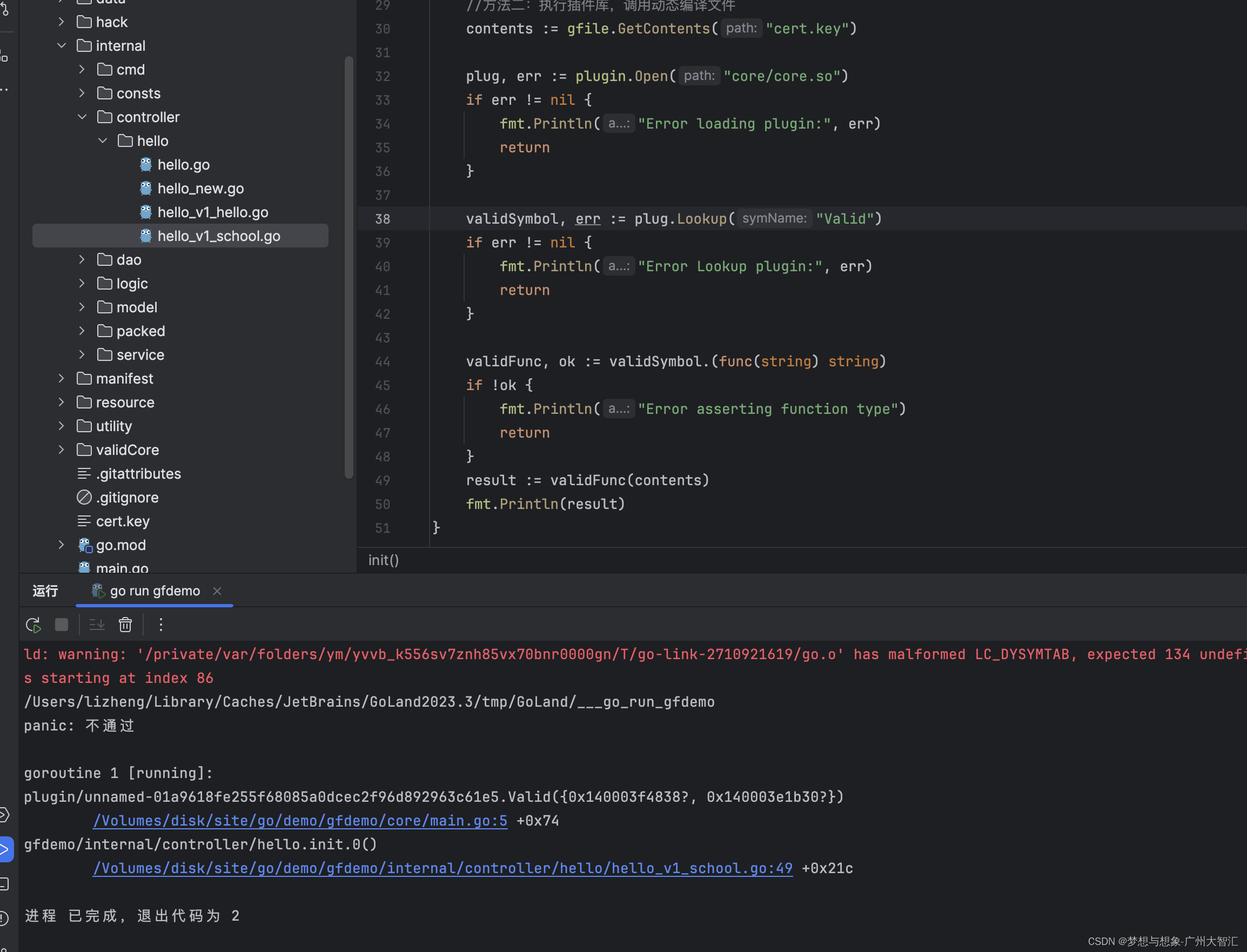
go执行静态二进制文件和执行动态库文件
目的和需求：部分go的核心文件不开源，例如验证，主程序核心逻辑等等 第一个想法，把子程序代码打包成静态文件，然后主程序执行 子程序 package mainimport ("fmt""github.com/gogf/gf/v2/os/gfile"…...
通过示例解释序列化和反序列化-Java
序列化和反序列化是Java（以及通常的编程）中涉及将对象转换为字节流，以及反之的过程。当你需要传输或存储对象的状态时特别有用，比如将其通过网络发送或持久化到文件中。 序列化： 定义：序列化是将对象的状…...
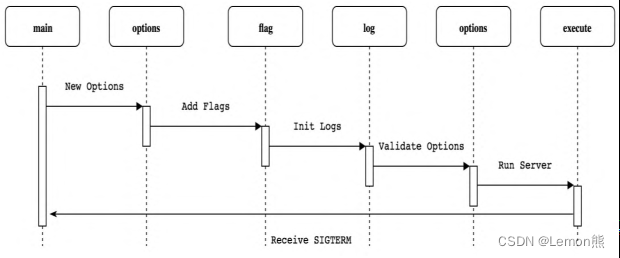
k8s源码阅读环境配置
源码阅读环境配置 k8s代码的阅读可以让我们更加深刻的理解k8s各组件的工作原理，同时提升我们Go编程能力。 IDE使用Goland，代码阅读环境需要进行如下配置： 从github上下载代码：https://github.com/kubernetes/kubernetes在GOPATH目…...
铭豹扩展坞 USB转网口 突然无法识别解决方法
当 USB 转网口扩展坞在一台笔记本上无法识别，但在其他电脑上正常工作时，问题通常出在笔记本自身或其与扩展坞的兼容性上。以下是系统化的定位思路和排查步骤，帮助你快速找到故障原因： 背景： 一个M-pard（铭豹）扩展坞的网卡突然无法识别了，扩展出来的三个USB接口正常。…...
React 第五十五节 Router 中 useAsyncError的使用详解
前言 useAsyncError 是 React Router v6.4 引入的一个钩子，用于处理异步操作（如数据加载）中的错误。下面我将详细解释其用途并提供代码示例。 一、useAsyncError 用途 处理异步错误：捕获在 loader 或 action 中发生的异步错误替…...
【SpringBoot】100、SpringBoot中使用自定义注解+AOP实现参数自动解密
在实际项目中，用户注册、登录、修改密码等操作，都涉及到参数传输安全问题。所以我们需要在前端对账户、密码等敏感信息加密传输，在后端接收到数据后能自动解密。 1、引入依赖 <dependency><groupId>org.springframework.boot</groupId><artifactId...
【算法训练营Day07】字符串part1
文章目录 反转字符串反转字符串II替换数字 反转字符串 题目链接：344. 反转字符串 双指针法，两个指针的元素直接调转即可 class Solution {public void reverseString(char[] s) {int head 0;int end s.length - 1;while(head < end) {char temp …...
代理篇12|深入理解 Vite中的Proxy接口代理配置
在前端开发中，常常会遇到 跨域请求接口 的情况。为了解决这个问题，Vite 和 Webpack 都提供了 proxy 代理功能，用于将本地开发请求转发到后端服务器。 什么是代理（proxy）？ 代理是在开发过程中，前端项目通过开发服务器，将指定的请求“转发”到真实的后端服务器，从而绕…...
Pinocchio 库详解及其在足式机器人上的应用
Pinocchio 库详解及其在足式机器人上的应用 Pinocchio (Pinocchio is not only a nose) 是一个开源的 C 库，专门用于快速计算机器人模型的正向运动学、逆向运动学、雅可比矩阵、动力学和动力学导数。它主要关注效率和准确性，并提供了一个通用的框架&…...
SiFli 52把Imagie图片，Font字体资源放在指定位置，编译成指定img.bin和font.bin的问题
分区配置 (ptab.json) img 属性介绍： img 属性指定分区存放的 image 名称，指定的 image 名称必须是当前工程生成的 binary 。 如果 binary 有多个文件，则以 proj_name:binary_name 格式指定文件名， proj_name 为工程 名&…...
CSS | transition 和 transform的用处和区别
省流总结： transform用于变换/变形，transition是动画控制器 transform 用来对元素进行变形，常见的操作如下，它是立即生效的样式变形属性。 旋转 rotate(角度deg)、平移 translateX(像素px)、缩放 scale(倍数)、倾斜 skewX(角度…...
【p2p、分布式，区块链笔记 MESH】Bluetooth蓝牙通信 BLE Mesh协议的拓扑结构 定向转发机制
目录 节点的功能承载层（GATT/Adv）局限性： 拓扑关系定向转发机制定向转发意义 CG 节点的功能 节点的功能由节点支持的特性和功能决定。所有节点都能够发送和接收网格消息。节点还可以选择支持一个或多个附加功能，如 Configuration …...
渗透实战PortSwigger靶场：lab13存储型DOM XSS详解
进来是需要留言的，先用做简单的 html 标签测试 发现面的</h1>不见了 数据包中找到了一个loadCommentsWithVulnerableEscapeHtml.js 他是把用户输入的<>进行 html 编码，输入的<>当成字符串处理回显到页面中，看来只是把用户输…...